「题解」解决二进制数中1的个数
🐶博主主页:@ᰔᩚ. 一怀明月ꦿ
❤️🔥专栏系列:线性代数,C初学者入门训练
🔥座右铭:“不要等到什么都没有了,才下定决心去做”
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀
目录
🐰取余取模法
🐰按位与法
🐰n=n&(n-1)法
🐰随记
🐰取余取模法
我们这里求的二进制数的1的个数求的是补码中1的个数
这种方法和十进制取余取模类似的,只是把10换成了2,例如:12345
12345%10=5
12345/10=1234
1234%10=4
1234/10=123
......
二进制也一样,例如:12
12%2=0
12/2=6
6%2=0
6/2=3
3%2=1
1/2=0
1%2=1
#include<stdio.h> int main() {int a=-1,count=0,num=0;unsigned int b=a;while(b){num=b%2;b/=2;if(num==1){count++;}}printf("%d\n",count);return 0; }这里负数也不用担心,我们把负数的补码转化为无符号数,这样也可以的到负数的补码了。
🐰按位与法
这种方法就是,利用按位与的性质,a&b,a和b相同的数就为相同的数,a和b不同的数则为0,例如,a=1000 0011 b=0110 0001
c=a&b
1000 0011
0110 0001
c=0000 0001
如果我们一个数a&1,且每次按位与完,我们就右移一位>>1,例如,a=12=1100
1100&1: 1100
1
num:0
a>>1: 1100>>1=0110
0110&1: 0110
1
num:0
a>>1: 0110>>1=0011
0011&1: 0011
1
num:1
a>>1: 0011>>1=0001
0001&1:0001
1num:1
a>>1: 0001>>1=0000
0000&1: 0000
1
num:0
然后统计num为1的次数就可以了
#include<stdio.h> int main() {int a=-1,count=0,num=0;for(int i=0;i<32;i++){num=a&1;if(num==1){count++;}a=a>>1;}printf("%d\n",count);return 0; }
🐰n=n&(n-1)法
只运算一次,n的二进制中最右边的一个1就会消失,例如n=1100
n: 1100
n-1: 1011
n&(n-1): 1000
n: 1000
n-1: 0111
n&(n-1): 0000
然后,统计n经历了几次n&(n-1)后,变为0的
#include<stdio.h> int main() {int a=-1,count=0;int num=a;while(num){num=num&(num-1);count++;}printf("%d\n",count);return 0; }这三种方法中,n=n&(n-1)法 是效率最高的一种方法
我们在判断一个数是否是2的次幂数,也可以用n=n&(n-1)法 ,因为2的次幂数又个特点,就是二进制只有一个1,例如
2^0: 0001
2^1: 0010
2^2: 0100
2^3: 1000
......
#include<stdio.h> int main() {int num=102;num=num&(num-1);if(num==0){printf("是\n");}else{printf("不是\n");}return 0; }
🐰随记
今天还使用到了一些小的知识点:
1.全局变量不初始化,就是默认为0
2.如果说一个整数和一个无符号整形数比较时,要被转化为两个无符号数比较例如:a=-1,sizeof(a)
if(a>sizeof(a))
这里sizeof(a)=4,sizeof(a)得到是一个无符号数,比较时a得转化为无符号数
a=-1:原码:10000000000000000000000000000001
反码:1111111111111111111111111111111111111111110
补码:1111111111111111111111111111111111111111111
当a转化为无符号数时,1111111111111111111111111111111111111111111这就是原码,这将是一个非常大的数,肯定大于sizeof(a)
3.栈区的使用习惯,先使用高地址,再使用低地址(常规情况下,release就除外了)
4.大端字节序:把一个数据的低字节的数据,存放在高地址处,把高字节的数据,存放在低地址处
小端字节序:把一个数据的低字节的数据,存放在低地址处,把高字节的数据,存放在高地址处
🌸🌸🌸如果大家还有不懂或者建议都可以发在评论区,我们共同探讨,共同学习,共同进步。谢谢大家! 🌸🌸🌸
相关文章:

「题解」解决二进制数中1的个数
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练 🔥座右铭:“不要等到什么都没有了,才下定决心去做” 🚀🚀🚀大家觉不错…...

泛型详解.
1 泛型的引入 问题:我们之前实现过的顺序表,只能保存 int 类型的元素,如果现在需要保存 指向 Person 类型对象的引用的顺序表,请问应该如何解决?如果又需要保存指向 Book 对象类型的引用呢? 之前写的顺序表…...

Vue 3.0 响应性 深入响应性原理 【Vue3 从零开始】
现在是时候深入了!Vue 最独特的特性之一,是其非侵入性的响应性系统。数据模型是被代理的 JavaScript 对象。而当你修改它们时,视图会进行更新。这让状态管理非常简单直观,不过理解其工作原理同样重要,这样你可以避开一…...
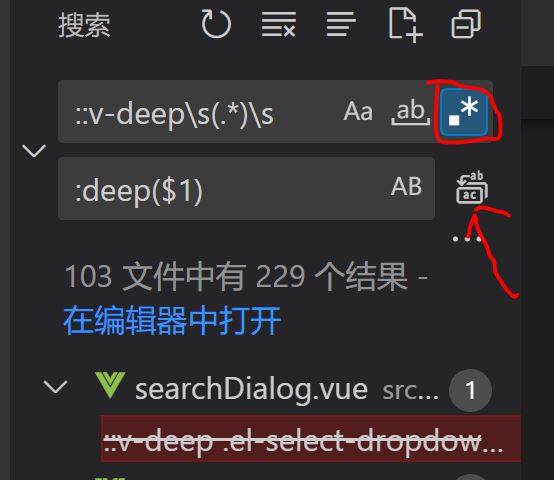
升级 vue3 常见问题总汇
Ⅰ、前言 虽然 vue3 是没有删除 vue2 的 选项式 API , 但是我们升级vue3 还是需要修改很多问题的下面来看看我们升级常见的一些问题 👇 文章目录Ⅰ、前言Ⅱ、解决兼容问题1、路由的创建方式2、路由的方法变化3、升级 vuex 到 4.x4、作用域 插槽语法修改…...

汽车 Automotive > T-BOX GNSS高精定位测试相关知识
参考:https://en.wikipedia.org/wiki/Global_Positioning_SystemGPS和GNSS的关系GPS(Global Positioning System),全球定位系统是美国军民两用的导航定位卫星系统,GPS包含双频信号,频点L1、L2和L5GNSS&…...

大数据面试核心101问【大厂超级喜欢这些题】
之前出过《史上最全的大数据开发八股文》这篇文章,同学们都觉得还不错,但是有些同学觉得那个背起来还是有些吃力,于是我再次回顾了自己之前面试所有大厂的一些面试题以及牛客上面的一些面经,然后总结了频率问的最高的101问&#x…...

代码随想录算法训练营第四十八天 | leetcode 121. 买卖股票的最佳时机,122.买卖股票的最佳时机II
代码随想录算法训练营第四十八天 | leetcode 121. 买卖股票的最佳时机,122.买卖股票的最佳时机II121. 买卖股票的最佳时机122.买卖股票的最佳时机II121. 买卖股票的最佳时机 题目: 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支…...

RAD 11.3 delphi和C++改进后新增、废弃及优化的功能
RAD 11.3 delphi和C改进后新增和废弃的功能 目录 RAD 11.3 delphi和C改进后新增和废弃的功能 一、版本RAD 11.3 delphi和C改进后新增功能 1、官方视频位置: 2、官方文档的链接位置: 二、版本RAD 11.3 delphi和C改进后废弃的功能 2.1、编译器不再使…...

【C++】引用
🏖️作者:malloc不出对象 ⛺专栏:C的学习之路 👦个人简介:一名双非本科院校大二在读的科班编程菜鸟,努力编程只为赶上各位大佬的步伐🙈🙈 目录前言一、引用1.1 引用概念1.2 引用特性…...
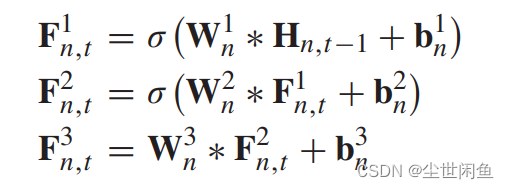
LPNet for Image Derain
Lightweight Pyramid Networks for Image Deraining前置知识高斯-拉普拉斯金字塔图像中的高频信息和低频信息为什么高斯-拉普拉斯金字塔可以实现去雨?可能性分析网络结构整体结构:子网结构:递归块结构:后续补充代码 前置知识 这…...
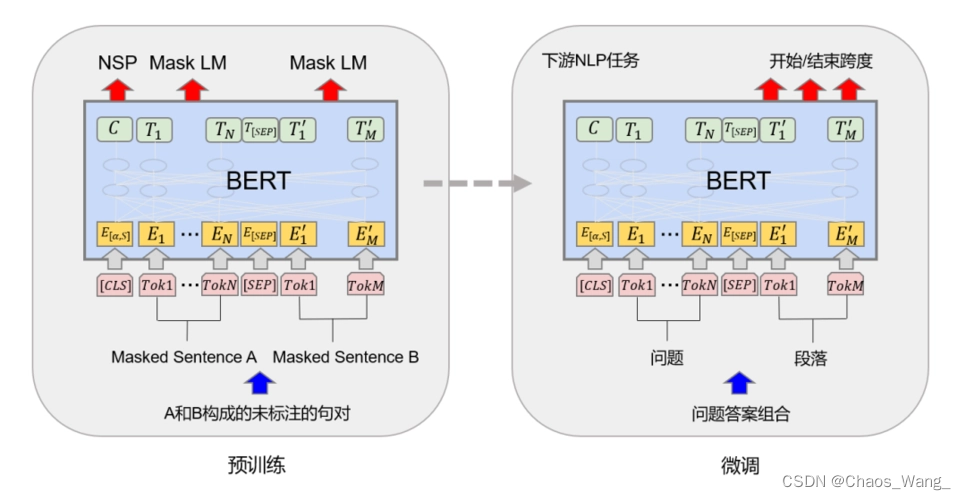
【NLP相关】基于现有的预训练模型使用领域语料二次预训练
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...

使用git进行项目管理--git使用及其常用命令
使用git进行项目管理 文章目录 使用git进行项目管理git使用1.添加用户名字2.添加用户邮箱3.git初始化4.add5.commit6.添加到gitee仓库7.推送到gitee8.切换版本git常用命令git add把指定的文件添加到暂存区中添加所有修改、已删除的文件到暂存区中添加所有修改、已删除、新增的文…...

Mybatis_CRUD使用
目录1 Mybatis简介环境说明:预备知识:1.1 定义1.2 持久化为什么需要持久化服务呢?1.3 持久层1.4 为什么需要Mybatis2 依赖配置3 CRUDnamespaceselect (查询用户数据)※传值方式:于方法中传值使用Map传值insert (插入用…...

JVM的过程内分析和过程间分析有什么区别?
问: 目前所有常见的Java虚拟机对过程间分析的支持都相 当有限,要么借助大规模的方法内联来打通方法间的隔阂,以过程内分析(Intra-Procedural Analysis, 只考虑过程内部语句,不考虑过程调用的分析ÿ…...

LearnDash测验报告如何帮助改进您的课程
某一个场景。Pennywell 大学有一门课程“Introduction to Linear Algebra”。上学期进行了两次测验。20% 的学生在第一次测验中不及格,而 80% 在第二次测验中不及格。在进一步评估中,观察到第一次测验不及格的学生在第二次测验中也不及格。在第二次测验中…...
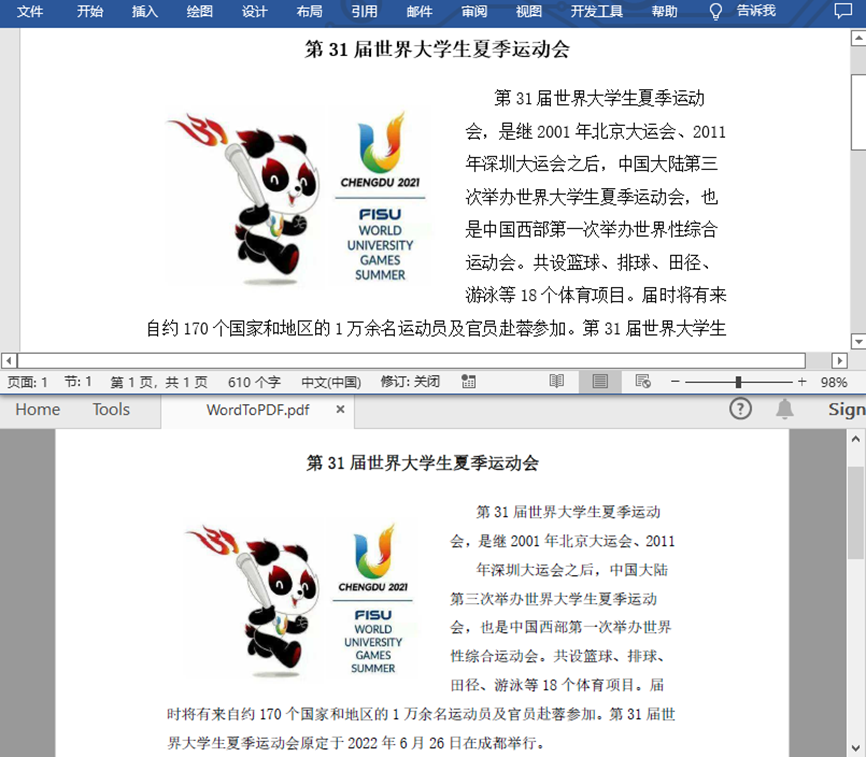
如何通过Java将Word转换为PDF
Word是我们日常编辑文档内容时十分常用的一种文档格式。但相比之下,PDF文档的格式、布局更为固定,不易被更改。在保存或传输较为重要的文档内容时,PDF文档格式也时很多人的不二选择。很多时候我们都会遇到需要将Word转换为PDF的情况。下面我就…...
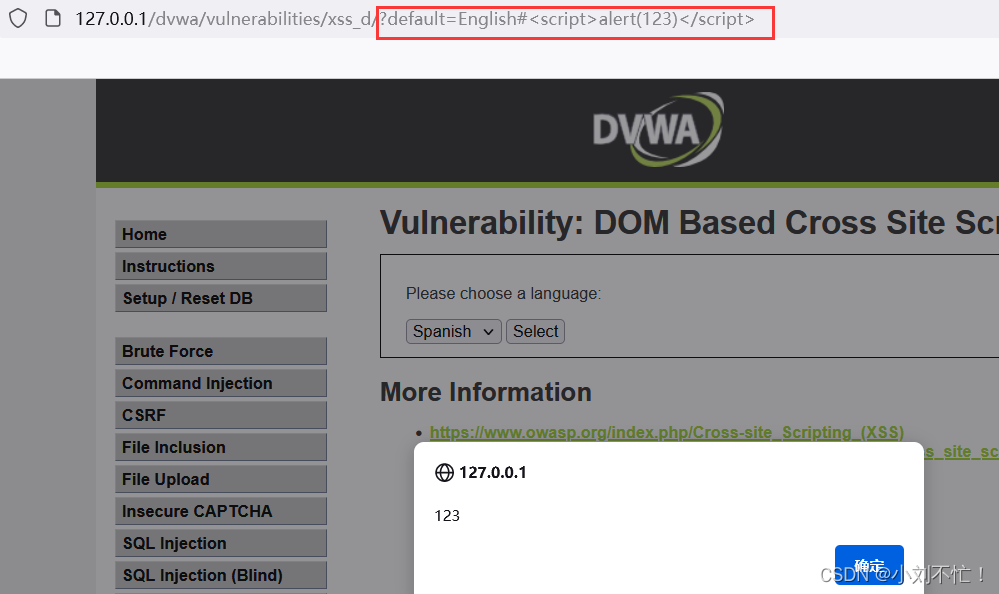
DOM型XSS
DOM型XSSDOM是什么DOM型XSSDOM型XSS实操DOM是什么 DOM就是Document。 文档是由节点构成的集合,在DOM里存在许多不同类型的节点,主要有:元素节点、文本节点,属性节点。 元素节点:好比< body >< p >< h …...
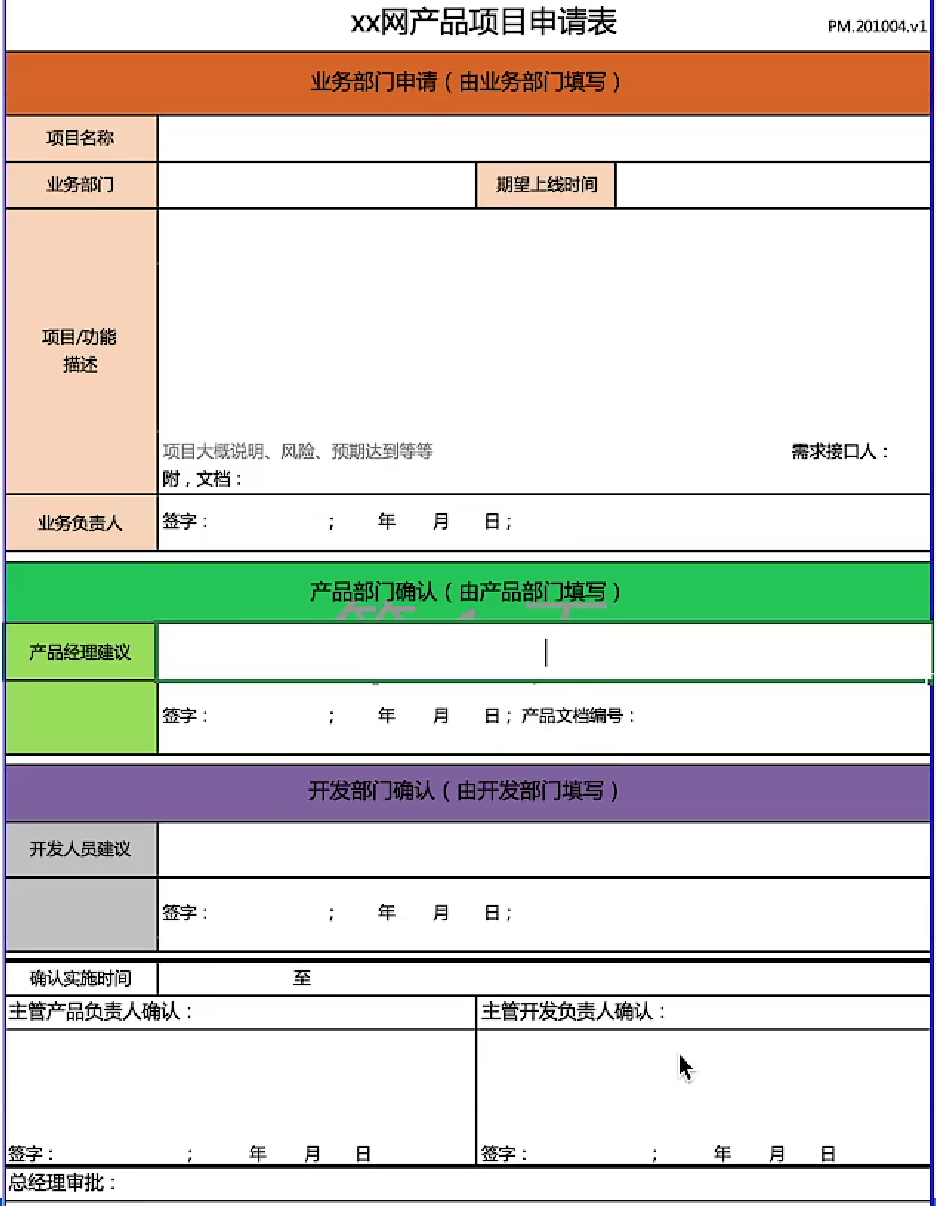
04-项目立项:项目方案、可行性分析、产品规划、立项评审
文章目录4.1 项目方案立项阶段4.2 可行性分析4.3 产品规划4.4 立项评审4.4.1 立项说明书的主要内容4.4.2 立项评审流程章节总结4.1 项目方案 学习目标: 能够输出产品项目方案 项目开发设计流程的主要阶段: 立项阶段 → 设计阶段 → 开发阶段 → 测试阶…...
)
数据分享|NPP VIIRS夜间灯光数据(2012-2020逐月)
2011年10月美国的“索米”国家极轨卫星伙伴卫星(Suomi National Polar-orbiting Partnership or Suomi NPP)发射,它搭载的VIIRS传感器上有一个称为DNB(Day Night Band)的波段能够在500米分辨率(比原来的OLS提高6倍)的尺度上对地表开展每天覆盖全球一次的高灵敏度(比OLS提…...

网络概论笔记
概论 网络研究的是节点和边 移动互联到物联网时代,只有有互联网,网络就不会落伍 协议:对等层面的实体固定的通信规则 协议包括:语法,语义,格式,次序,动作 网络是任意连接的 服务…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
