使用Python通过拉马努金公式快速求π
使用Python通过拉马努金公式快速求π
一、前言
π是一个数学常数,定义为:圆的周长与直径的比值。
π是一个无理数,也是一个超越数,它的小数部分无限不循环。
π可以用来精确计算圆周长、圆面积、球体积等几何形状的关键值。
有关π的有趣知识有很多,例如:
- π在数学中有很多重要的应用,例如欧拉公式e^(iπ)=-1,这个公式被称为“数学之美”,因为它将5个看似无关的符号紧密地联系了起来。
- π符号是由瑞士数学家欧拉在1736年首次使用的。之前,人们通常用分数或无穷级数来表示圆周率。
- π是希腊语“周长”的开头字母。
- π的小数部分中,第762位到第766位是“99999”,这被称为“Feynman点”,因为物理学家费曼(Richard Feynman)曾经说过,如果他能记住π的所有数字,他就会以这五个9为结尾。
- 3月14日被称为“圆周率日”,因为这个日期的美式写法是3/14,和π的前两位数字相同。
- 7月22日也被称为“圆周率近似日”,因为这个日期的欧式写法是22/7,和π的一个常用近似值相同。
π是否是一个正规数还没有确定,正规数是指在任何进制下,它的小数部分包含了所有可能出现的数字序列。但是目前还没有确定的答案。
一种可能的情况是,π是一个正规数,也就是说它在任何进制下的小数部分包含了所有可能出现的数字序列,并且每个数字出现的概率都相同。如果这样的话,由于π是一个无限不循环小数,那么π中所有数字出现的概率确实均等。也就是说,我们在π中找到任何数字的组合,比如: - 所有人的生日
- 所有人的银行卡密码
这里介绍一个在π中查找特殊数字组合起始位置的网站:
http://www.subidiom.com/pi/pi.asp
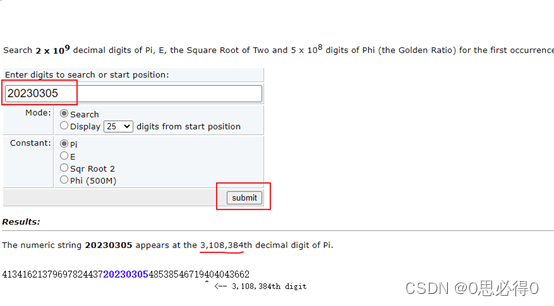
只要输入一个你想在π中找寻的数字组合,这个网站就会通过在π中搜索并反馈搜索结果给你:
- 进入网站,输入想要查询的数字组合:20230305
- 点击
submit - 等待查询结果:3108384
1.1 为什么要算π
π是一个无理数,也就是说它不能用两个整数的比值来表示。它的小数部分是无限不循环的,目前已经计算出了超过50万亿位。
实际上,如果用圆周公式来计算整个宇宙的周长,只需要使用π的前40位就可以精确计算出来了,我们假设宇宙的直径是93亿光年,那么它的周长就是2π×93亿光年。如果我们用π的前40位来计算这个值,那么误差就不到一个质子的直径。也就是说,用π的前40位就足以精确地描述宇宙的大小了。
那为什么还要用超级计算机不停的计算π呢?用超级计算机不停的算π,是因为人们对这个神奇的数有着强烈的好奇心和探索欲。
一方面,计算π可以检验超级计算机的性能和稳定性,也可以推动计算方法和软件技术的发展。
另一方面,计算π也有一些实际应用,比如密码学、随机数生成、数据压缩等。
不过,由于π是一个无理数,它的小数部分是无限不循环的,所以用任何有限的资源都无法算尽它。
1.2 π的求法
π在历史上被不同的文明用不同的方法估算过,最早可以追溯到4000年前的古埃及和巴比伦。其中一个简单的方法是用绳子测量圆形物体的周长和直径,然后计算它们的比值。
求π值的方法有很多种,比如:
阿基米德法:用正多边形逼近圆,计算其周长和面积,得到π的上下界。
无穷级数法:利用一些收敛速度快的无穷级数公式,如莱布尼茨公式、马青公式等,不断求和得到π的近似值。
莱布尼茨公式:π/4 = 1 - 1/3 + 1/5 - 1/7 + …
马青公式:π = 16 arctan(1/5) - 4 arctan(1/239)
阿基米德法变形:π = 2 + 2/3 + 2/3x2/5 + 2/3x2/5x3/7 + …
蒙特卡罗法:用随机数模拟撒豆子或者投针实验,统计落在圆内和圆外的比例,得到π的近似值。
今天要介绍的是是拉马努金公式(Ramanujan formula),它是印度数学家拉马努金(Srinivasa Ramanujan)在1910年发现的一系列级数公式,可以用来快速计算π的近似值。这个公式每计算一项可以得到8位的十进制精度。
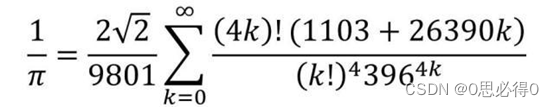
二、准备
2.1 高精度库
在Python中,默认的小数位数为17位,如果想要计算更多的小数位,则需要专门的库。这里使用decimal库。decimal是一个Python内置库,无需安装。可以直接导入使用。
2.2 π的值
因为后面要涉及到核对,所以需要准备正确的π的前xx位,这里是使用了前1万位。如下:
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989380952572010654858632788659361533818279682303019520353018529689957736225994138912497217752834791315155748572424541506959508295331168617278558890750983817546374649393192550604009277016711390098488240128583616035637076601047101819429555961989467678374494482553797747268471040475346462080466842590694912933136770289891521047521620569660240580381501935112533824300355876402474964732639141992726042699227967823547816360093417216412199245863150302861829745557067498385054945885869269956909272107975093029553211653449872027559602364806654991198818347977535663698074265425278625518184175746728909777727938000816470600161452491921732172147723501414419735685481613611573525521334757418494684385233239073941433345477624168625189835694855620992192221842725502542568876717904946016534668049886272327917860857843838279679766814541009538837863609506800642251252051173929848960841284886269456042419652850222106611863067442786220391949450471237137869609563643719172874677646575739624138908658326459958133904780275900994657640789512694683983525957098258226205224894077267194782684826014769909026401363944374553050682034962524517493996514314298091906592509372216964615157098583874105978859597729754989301617539284681382686838689427741559918559252459539594310499725246808459872736446958486538367362226260991246080512438843904512441365497627807977156914359977001296160894416948685558484063534220722258284886481584560285060168427394522674676788952521385225499546667278239864565961163548862305774564980355936345681743241125150760694794510965960940252288797108931456691368672287489405601015033086179286809208747609178249385890097149096759852613655497818931297848216829989487226588048575640142704775551323796414515237462343645428584447952658678210511413547357395231134271661021359695362314429524849371871101457654035902799344037420073105785390621983874478084784896833214457138687519435064302184531910484810053706146806749192781911979399520614196634287544406437451237181921799983910159195618146751426912397489409071864942319615679452080951465502252316038819301420937621378559566389377870830390697920773467221825625996615014215030680384477345492026054146659252014974428507325186660021324340881907104863317346496514539057962685610055081066587969981635747363840525714591028970641401109712062804390397595156771577004203378699360072305587631763594218731251471205329281918261861258673215791984148488291644706095752706957220917567116722910981690915280173506712748583222871835209353965725121083579151369882091444210067510334671103141267111369908658516398315019701651511685171437657618351556508849099898599823873455283316355076479185358932261854896321329330898570642046752590709154814165498594616371802709819943099244889575712828905923233260972997120844335732654893823911932597463667305836041428138830320382490375898524374417029132765618093773444030707469211201913020330380197621101100449293215160842444859637669838952286847831235526582131449576857262433441893039686426243410773226978028073189154411010446823252716201052652272111660396665573092547110557853763466820653109896526918620564769312570586356620185581007293606598764861179104533488503461136576867532494416680396265797877185560845529654126654085306143444318586769751456614068007002378776591344017127494704205622305389945613140711270004078547332699390814546646458807972708266830634328587856983052358089330657574067954571637752542021149557615814002501262285941302164715509792592309907965473761255176567513575178296664547791745011299614890304639947132962107340437518957359614589019389713111790429782856475032031986915140287080859904801094121472213179476477726224142548545403321571853061422881375850430633217518297986622371721591607716692547487389866549494501146540628433663937900397692656721463853067360965712091807638327166416274888800786925602902284721040317211860820419000422966171196377921337575114959501566049631862947265473642523081770367515906735023507283540567040386743513622224771589150495309844489333096340878076932599397805419341447377441842631298608099888687413260472156951623965864573021631598193195167353812974167729478672422924654366800980676928238280689964004824354037014163149658979409243237896907069779422362508221688957383798623001593776471651228935786015881617557829735233446042815126272037343146531977774160319906655418763979293344195215413418994854447345673831624993419131814809277771038638773431772075456545322077709212019051660962804909263601975988281613323166636528619326686336062735676303544776280350450777235547105859548702790814356240145171806246436267945612753181340783303362542327839449753824372058353114771199260638133467768796959703098339130771098704085913374641442822772634659470474587847787201927715280731767907707157213444730605700733492436931138350493163128404251219256517980694113528013147013047816437885185290928545201165839341965621349143415956258658655705526904965209858033850722426482939728584783163057777560688876446248246857926039535277348030480290058760758251047470916439613626760449256274204208320856611906254543372131535958450687724602901618766795240616342522577195429162991930645537799140373404328752628889639958794757291746426357455254079091451357111369410911939325191076020825202618798531887705842972591677813149699009019211697173727847684726860849003377024242916513005005168323364350389517029893922334517220138128069650117844087451960121228599371623130171144484640903890644954440061986907548516026327505298349187407866808818338510228334508504860825039302133219715518430635455007668282949304137765527939751754613953984683393638304746119966538581538420568533862186725233402830871123282789212507712629463229563989898935821167456270102183564622013496715188190973038119800497340723961036854066431939509790190699639552453005450580685501956730229219139339185680344903982059551002263535361920419947455385938102343955449597783779023742161727111723643435439478221818528624085140066604433258885698670543154706965747458550332323342107301545940516553790686627333799585115625784322988273723198987571415957811196358330059408730681216028764962867446047746491599505497374256269010490377819868359381465741268049256487985561453723478673303904688383436346553794986419270563872931748723320837601123029911367938627089438799362016295154133714248928307220126901475466847653576164773794675200490757155527819653621323926406160136358155907422020203187277605277219005561484255518792530343513984425322341576233610642506390497500865627109535919465897514131034822769306247435363256916078154781811528436679570611086153315044521274739245449454236828860613408414863776700961207151249140430272538607648236341433462351897576645216413767969031495019108575984423919862916421939949072362346468441173940326591840443780513338945257423995082965912285085558215725031071257012668302402929525220118726767562204154205161841634847565169998116141010029960783869092916030288400269104140792886215078424516709087000699282120660418371806535567252532567532861291042487761825829765157959847035622262934860034158722980534989650226291748788202734209222245339856264766914905562842503912757710284027998066365825488926488025456610172967026640765590429099456815065265305371829412703369313785178609040708667114965583434347693385781711386455873678123014587687126603489139095620099393610310291616152881384379099042317473363948045759314931405297634757481193567091101377517210080315590248530906692037671922033229094334676851422144773793937517034436619910403375111735471918550464490263655128162288244625759163330391072253837421821408835086573917715096828874782656995995744906617583441375223970968340800535598491754173818839994469748676265516582765848358845314277568790029095170283529716344562129640435231176006651012412006597558512761785838292041974844236080071930457618932349229279650198751872127267507981255470958904556357921221033346697499235630254947802490114195212382815309114079073860251522742995818072471625916685451333123948049470791191532673430282441860414263639548000448002670496248201792896476697583183271314251702969234889627668440323260927524960357996469256504936818360900323809293459588970695365349406034021665443755890045632882250545255640564482465151875471196218443965825337543885690941130315095261793780029741207665147939425902989695946995565761218656196733786236256125216320862869222103274889218654364802296780705765615144632046927906821207388377814233562823608963208068222468012248261177185896381409183903673672220888321513755600372798394004152970028783076670944474560134556417254370906979396122571429894671543578468788614445812314593571984922528471605049221242470141214780573455105008019086996033027634787081081754501193071412233908663938339529425786905076431006383519834389341596131854347546495569781038293097164651438407007073604112373599843452251610507027056235266012764848308407611830130527932054274628654036036745328651057065874882256981579367897669742205750596834408697350201410206723585020072452256326513410559240190274216248439140359989535394590944070469120914093870012645600162374288021092764579310657922955249887275846101264836999892256959688159205600101655256375678
三、代码
from decimal import Decimal, getcontext # 高精度小数库
from mdTools import ftDecTimeIt # 计算函数运行时长的装饰器
from math import factorial # 阶乘
from π import str_real_pi # π的真实值(前1万位小数) count_numbers = 5000 # 要计算的前N位,请勿超过10000,否则无数据核对
effective_numbers = int(count_numbers * 1.1) # 有效数字位数
print(f'本程序即将计算π的前:{count_numbers}位,并核对。') @ftDecTimeIt(1)
def count_π(prec=1000): getcontext().prec = prec # 设置有效的数字位数 x = 0 for k in range(int(prec / 8) + 1): # 这个公式每计算一项可以得到8位的十进制精度。 a = 2 * Decimal.sqrt(Decimal(2)) / 9801 b = factorial(4 * k) * (1103 + 26390 * k) c = pow(factorial(k), 4) * pow(396, 4 * k) x = x + a * b / c return 1 / x pi = count_π(effective_numbers)
# 核对
flag = True
for i in range(2, count_numbers): if str_real_pi[i] != str(pi)[i]: print(f'出错啦!出错的位数为:{i}, 该小数位正确的为:{str_real_pi[i]}, 错误的计算为:{str(pi)[i]}') flag = False break
if flag: print('核对无误!')
本程序即将计算π的前:5000位,并核对。
函数 count_π 运行 1 次的总耗时为:18.5894 秒
核对无误!
> 本程序即将计算π的前:5000位,并核对。
> 函数 count_π 运行 1 次的总耗时为:18.5894 秒
> 核对无误! 相关文章:
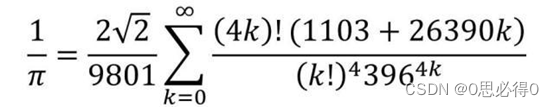
使用Python通过拉马努金公式快速求π
使用Python通过拉马努金公式快速求π 一、前言 π是一个数学常数,定义为:圆的周长与直径的比值。 π是一个无理数,也是一个超越数,它的小数部分无限不循环。 π可以用来精确计算圆周长、圆面积、球体积等几何形状的关键值。 有关…...

第六章 使用系统类提供国家语言支持 - 创建自定义语言环境
文章目录第六章 使用系统类提供国家语言支持 - 创建自定义语言环境创建自定义语言环境第六章 使用系统类提供国家语言支持 - 创建自定义语言环境 创建自定义语言环境 此示例将提供一个模板,用于使用自定义表创建自定义语言环境。自定义表将在 EBCDIC(美…...

「题解」解决二进制数中1的个数
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练 🔥座右铭:“不要等到什么都没有了,才下定决心去做” 🚀🚀🚀大家觉不错…...

泛型详解.
1 泛型的引入 问题:我们之前实现过的顺序表,只能保存 int 类型的元素,如果现在需要保存 指向 Person 类型对象的引用的顺序表,请问应该如何解决?如果又需要保存指向 Book 对象类型的引用呢? 之前写的顺序表…...

Vue 3.0 响应性 深入响应性原理 【Vue3 从零开始】
现在是时候深入了!Vue 最独特的特性之一,是其非侵入性的响应性系统。数据模型是被代理的 JavaScript 对象。而当你修改它们时,视图会进行更新。这让状态管理非常简单直观,不过理解其工作原理同样重要,这样你可以避开一…...
升级 vue3 常见问题总汇
Ⅰ、前言 虽然 vue3 是没有删除 vue2 的 选项式 API , 但是我们升级vue3 还是需要修改很多问题的下面来看看我们升级常见的一些问题 👇 文章目录Ⅰ、前言Ⅱ、解决兼容问题1、路由的创建方式2、路由的方法变化3、升级 vuex 到 4.x4、作用域 插槽语法修改…...

汽车 Automotive > T-BOX GNSS高精定位测试相关知识
参考:https://en.wikipedia.org/wiki/Global_Positioning_SystemGPS和GNSS的关系GPS(Global Positioning System),全球定位系统是美国军民两用的导航定位卫星系统,GPS包含双频信号,频点L1、L2和L5GNSS&…...

大数据面试核心101问【大厂超级喜欢这些题】
之前出过《史上最全的大数据开发八股文》这篇文章,同学们都觉得还不错,但是有些同学觉得那个背起来还是有些吃力,于是我再次回顾了自己之前面试所有大厂的一些面试题以及牛客上面的一些面经,然后总结了频率问的最高的101问&#x…...

代码随想录算法训练营第四十八天 | leetcode 121. 买卖股票的最佳时机,122.买卖股票的最佳时机II
代码随想录算法训练营第四十八天 | leetcode 121. 买卖股票的最佳时机,122.买卖股票的最佳时机II121. 买卖股票的最佳时机122.买卖股票的最佳时机II121. 买卖股票的最佳时机 题目: 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支…...

RAD 11.3 delphi和C++改进后新增、废弃及优化的功能
RAD 11.3 delphi和C改进后新增和废弃的功能 目录 RAD 11.3 delphi和C改进后新增和废弃的功能 一、版本RAD 11.3 delphi和C改进后新增功能 1、官方视频位置: 2、官方文档的链接位置: 二、版本RAD 11.3 delphi和C改进后废弃的功能 2.1、编译器不再使…...

【C++】引用
🏖️作者:malloc不出对象 ⛺专栏:C的学习之路 👦个人简介:一名双非本科院校大二在读的科班编程菜鸟,努力编程只为赶上各位大佬的步伐🙈🙈 目录前言一、引用1.1 引用概念1.2 引用特性…...
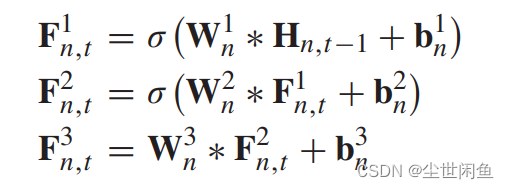
LPNet for Image Derain
Lightweight Pyramid Networks for Image Deraining前置知识高斯-拉普拉斯金字塔图像中的高频信息和低频信息为什么高斯-拉普拉斯金字塔可以实现去雨?可能性分析网络结构整体结构:子网结构:递归块结构:后续补充代码 前置知识 这…...
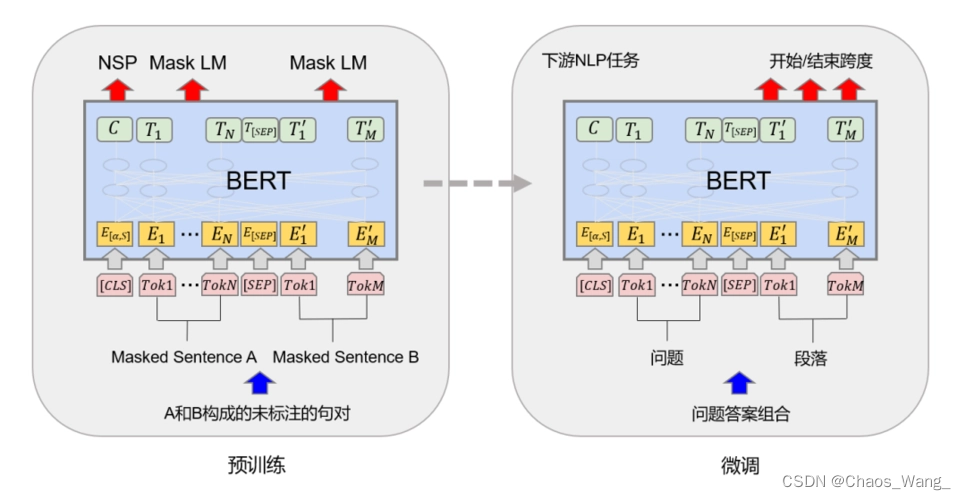
【NLP相关】基于现有的预训练模型使用领域语料二次预训练
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...

使用git进行项目管理--git使用及其常用命令
使用git进行项目管理 文章目录 使用git进行项目管理git使用1.添加用户名字2.添加用户邮箱3.git初始化4.add5.commit6.添加到gitee仓库7.推送到gitee8.切换版本git常用命令git add把指定的文件添加到暂存区中添加所有修改、已删除的文件到暂存区中添加所有修改、已删除、新增的文…...

Mybatis_CRUD使用
目录1 Mybatis简介环境说明:预备知识:1.1 定义1.2 持久化为什么需要持久化服务呢?1.3 持久层1.4 为什么需要Mybatis2 依赖配置3 CRUDnamespaceselect (查询用户数据)※传值方式:于方法中传值使用Map传值insert (插入用…...

JVM的过程内分析和过程间分析有什么区别?
问: 目前所有常见的Java虚拟机对过程间分析的支持都相 当有限,要么借助大规模的方法内联来打通方法间的隔阂,以过程内分析(Intra-Procedural Analysis, 只考虑过程内部语句,不考虑过程调用的分析ÿ…...

LearnDash测验报告如何帮助改进您的课程
某一个场景。Pennywell 大学有一门课程“Introduction to Linear Algebra”。上学期进行了两次测验。20% 的学生在第一次测验中不及格,而 80% 在第二次测验中不及格。在进一步评估中,观察到第一次测验不及格的学生在第二次测验中也不及格。在第二次测验中…...
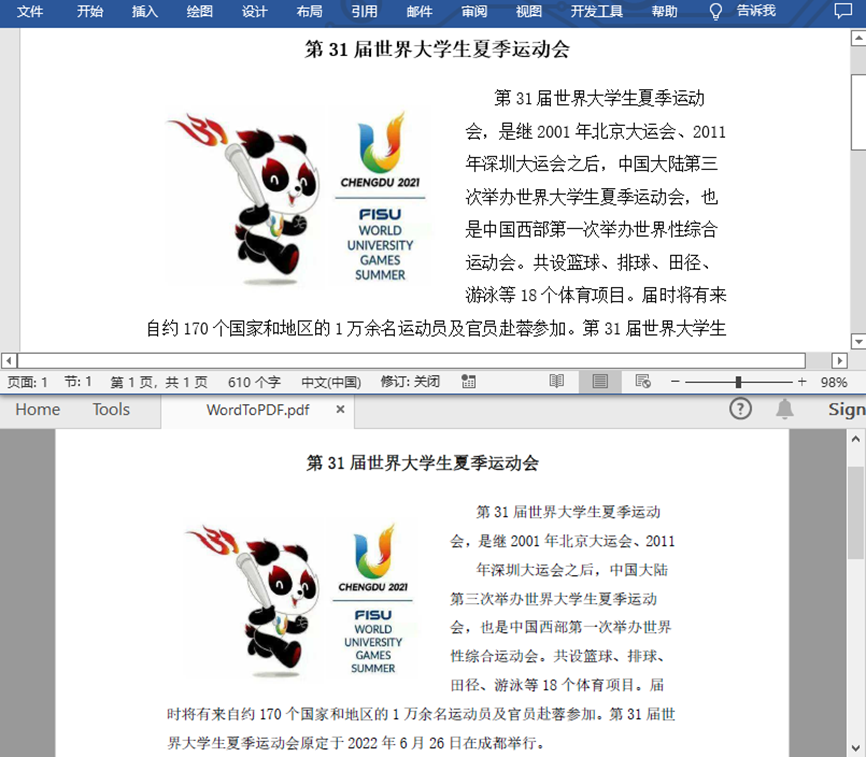
如何通过Java将Word转换为PDF
Word是我们日常编辑文档内容时十分常用的一种文档格式。但相比之下,PDF文档的格式、布局更为固定,不易被更改。在保存或传输较为重要的文档内容时,PDF文档格式也时很多人的不二选择。很多时候我们都会遇到需要将Word转换为PDF的情况。下面我就…...
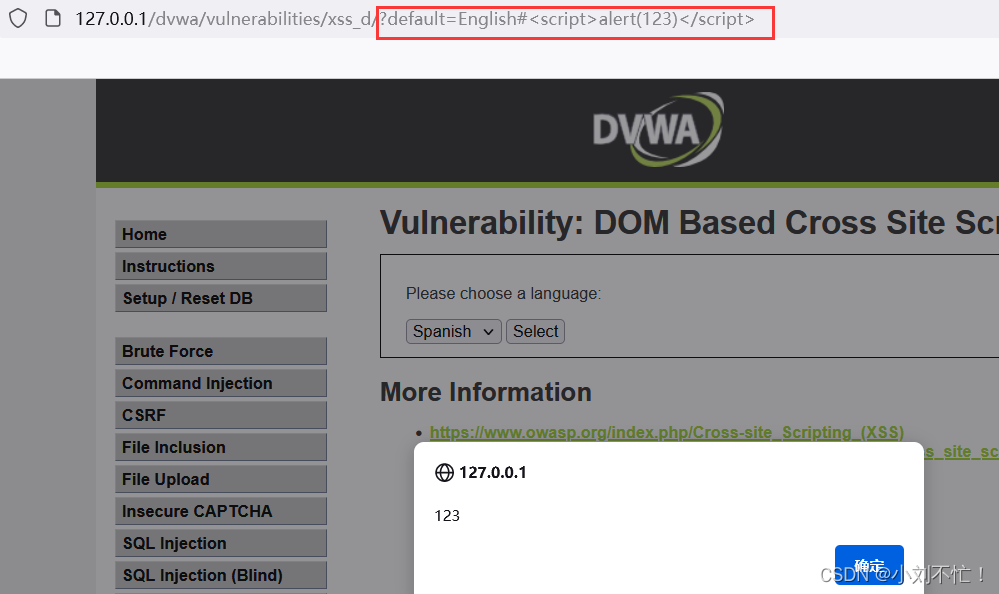
DOM型XSS
DOM型XSSDOM是什么DOM型XSSDOM型XSS实操DOM是什么 DOM就是Document。 文档是由节点构成的集合,在DOM里存在许多不同类型的节点,主要有:元素节点、文本节点,属性节点。 元素节点:好比< body >< p >< h …...
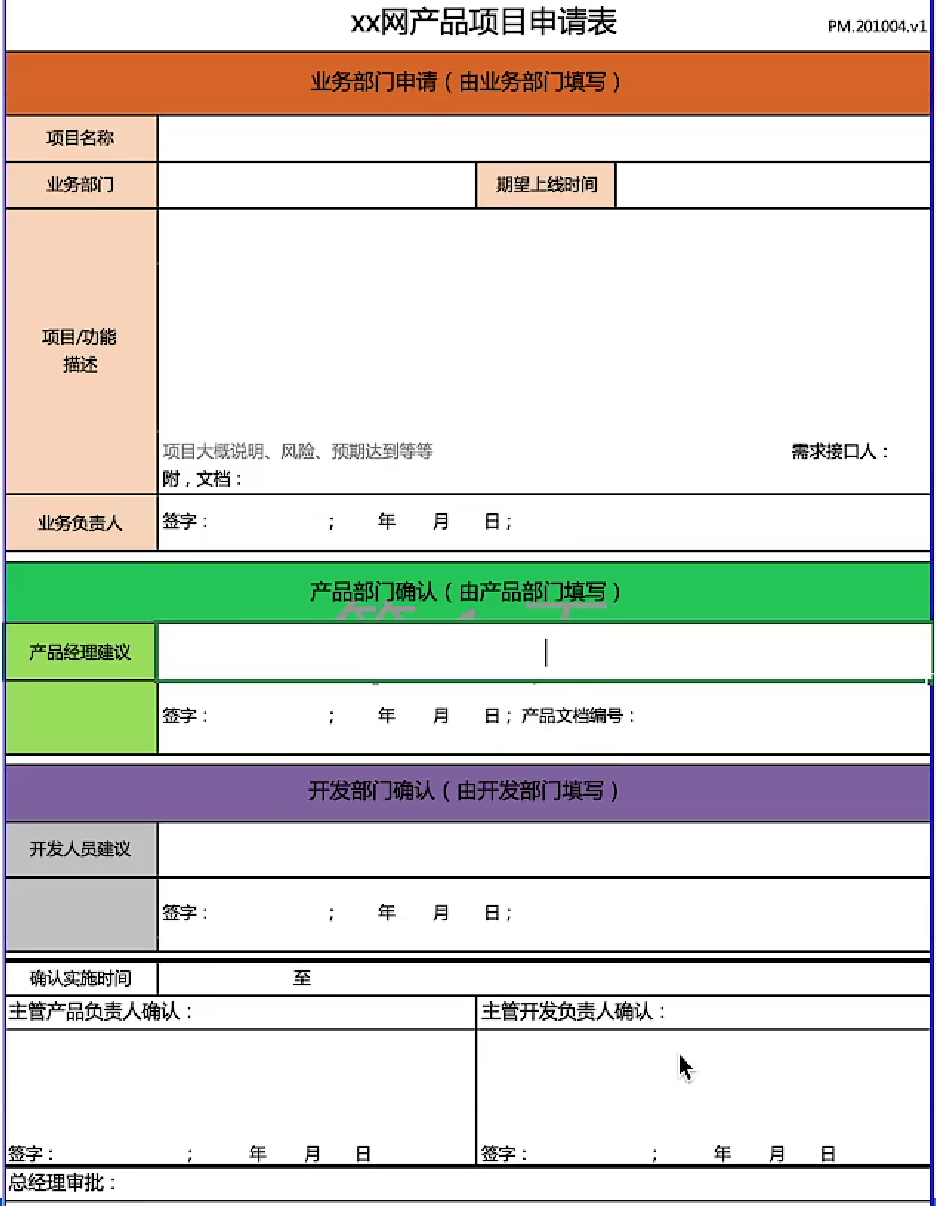
04-项目立项:项目方案、可行性分析、产品规划、立项评审
文章目录4.1 项目方案立项阶段4.2 可行性分析4.3 产品规划4.4 立项评审4.4.1 立项说明书的主要内容4.4.2 立项评审流程章节总结4.1 项目方案 学习目标: 能够输出产品项目方案 项目开发设计流程的主要阶段: 立项阶段 → 设计阶段 → 开发阶段 → 测试阶…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
