当前位置： 首页 > news >正文

华为校招机试真题目录

news 2026/2/9 0:29:50

专栏介绍

本专栏将逐步收集历年华为校招算法真题

专栏权益

每篇博客都包含：

  • 算法考点解析（文字+画图）
  • 算法源码（支持 Java / JS / Python）

每晚9:00 ~ 11:00 在线答疑

真题目录

时间题目考点 or 实现
2022.11.27

相关文章：

华为校招机试真题目录

专栏介绍 本专栏将逐步收集历年华为校招算法真题 专栏权益 每篇博客都包含： 算法考点解析（文字+画图）算法源码（支持 Java / JS / Python）每晚9:00 ~ 11:00 在线答疑 真题目录 时间题目考点 or 实现2022.11.27...

编程日记 2023/5/16 22:40:21

EdgeYOLO学习笔记

EdgeYOLO学习笔记 EdgeYOLO: An Edge-Real-Time Object Detector Abstract 本文基于最先进的YOLO框架，提出了一种高效、低复杂度、无锚的目标检测器，该检测器可以在边缘计算平台上实时实现。为了有效抑制训练过程中的过拟合，我们开发了一种…...

编程日记 2023/5/16 22:40:17

【分布式】什么是分布式锁？正文揭晓

分布式锁的概念 分布式锁其实可以理解为：控制分布式系统有序的去对共享资源进行操作，通过互斥来保持一致性。 举个例子：假设共享的资源就是一个房子，里面有各种书，分布式系统就是要进屋看书的人， 分布式锁…...

编程日记 2023/5/16 22:40:16

超详细JDK1.8所有版本下载地址

JDK1.8即为JDK8，JDK8是目前是最成熟最稳定的版本，本文将详细介绍JDK1.8历史版本的下载方式。 在此附上JDK1.8安装与配置教程 超详细JDK1.8安装与配置 一、JDK官网 首先打开oracle官网，官网首页地址为 JDK官网首页地址 点击Products 点击…...

编程日记 2023/5/16 22:40:14

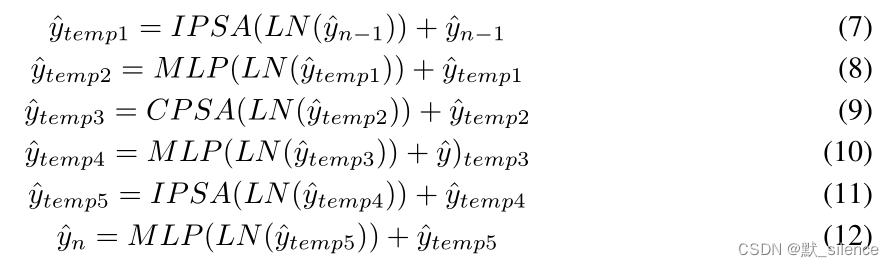
论文解析[11] CAT: Cross Attention in Vision Transformer

发表时间：2021 论文地址：https://arxiv.org/abs/2106.05786v1 文章目录摘要3 方法3.1 总体结构3.1.1 Inner-Patch Self-Attention Block3.1.2 Cross-Patch Self-Attention Block3.1.3 Cross Attention based Transformer结论摘要 使用图像patch来替换tr…...

编程日记 2023/5/16 22:40:08

嵌入式和Python（一）：python环境搭建的详细步骤

目录 ● 安装python ① 更新软件列表 ② 安装编译python需要用到的环境 ③ 下载python源码 ④ 解压源码包 ⑤ 配置 ⑥ 编译 ⑦ 安装 ● 建立软连接 说明 ① 删除原来的软连接 ② 在/usr/bin/目录创建软连接python，定向/usr/local/bin/python3.9 ③ 检查…...

编程日记 2023/5/16 22:40:06

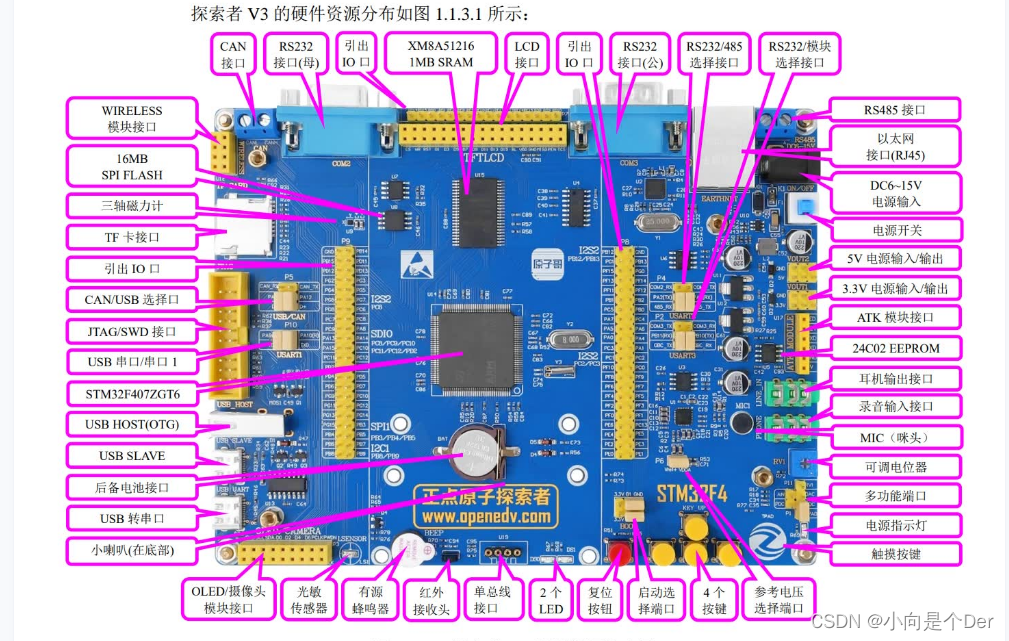
嵌入式学习笔记——STM32硬件基础知识

STM32开发硬件知识前言单片机参数主频位数STM32最小系统电源电路晶振电路复位电路BOOT选择电路调试接口电路其他电路本文重点本文参考博客链接前言 上一篇中我们重点是讲了一下怎么搭建开发环境以及怎么下载烧录的过程，这都是解决的电脑端的开发环境问题&#xff0…...

编程日记 2023/5/16 22:40:04

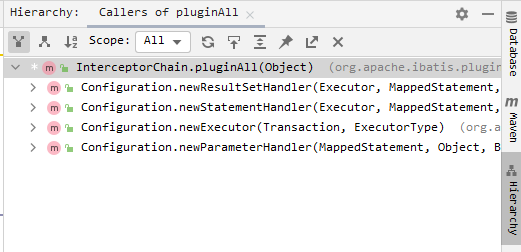
Mybatis插件开发及执行原理

mybatis源码下载 https://github.com/mybatis/mybatis-3，本文分析源码版本3.4.5 mybatis启动大致流程 在看这篇文章前，建议查看我另一篇文章，以了解框架启动的流程和框架中一些重要对象：https://blog.csdn.net/Aqu415/article/…...

编程日记 2023/5/16 22:40:00

vue父子组件通信，兄弟组件通信

目录 一、父子组件通信 1、子组件通过 props 获取父组件变量和父组件调用子组件中的方法(这两个都是父传子的思想) a:子组件通过 props 获取父组件变量 b:父组件调用子组件中的方法 2、父组件通过ref获取子组件变量和子组件调用父组件的方法（这两个都是子传父的…...

编程日记 2023/5/16 22:39:57

大数据技术之Hadoop集群配置

作者简介&#xff1a;大家好我是小唐同学(๑>؂<๑&#xff09;&#xff0c;好久不见&#xff0c;为梦想而努力的小唐又回来了&#xff0c;让我们一起加油&#xff01;&#xff01;&#xff01; 个人主页&#xff1a;小唐同学(๑>؂<๑&#xff09;的博客主页 目前…...

编程日记 2023/5/16 22:39:55

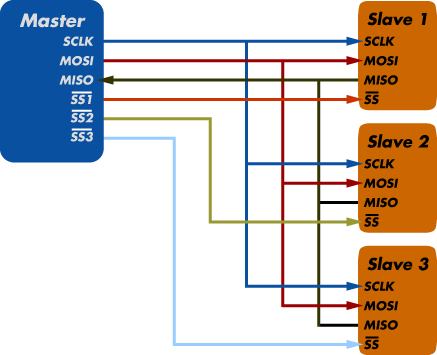
MicroBlaze系列教程（7）：AXI_SPI的使用(M25P16)

文章目录 AXI_SPI简介MicroBlaze硬件配置常用函数使用示例波形实测参考资料工程下载本文是Xilinx MicroBlaze系列教程的第7篇文章。 AXI_SPI简介 Xilinx AXI-SPI IP共有两个：一个是标准的AXI_SPI，即4线制SPI，CS、SCLK、MOSI和MISO，另一个是AXI_Quad SPI，支持配置成标准SP…...

编程日记 2023/5/16 22:39:53

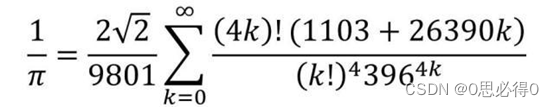
使用Python通过拉马努金公式快速求π

使用Python通过拉马努金公式快速求π 一、前言 π是一个数学常数&#xff0c;定义为&#xff1a;圆的周长与直径的比值。 π是一个无理数&#xff0c;也是一个超越数&#xff0c;它的小数部分无限不循环。 π可以用来精确计算圆周长、圆面积、球体积等几何形状的关键值。 有关…...

编程日记 2023/5/17 2:54:13

第六章 使用系统类提供国家语言支持 - 创建自定义语言环境

文章目录第六章 使用系统类提供国家语言支持 - 创建自定义语言环境创建自定义语言环境第六章 使用系统类提供国家语言支持 - 创建自定义语言环境 创建自定义语言环境 此示例将提供一个模板&#xff0c;用于使用自定义表创建自定义语言环境。自定义表将在 EBCDIC&#xff08;美…...

编程日记 2023/5/17 2:54:11

「题解」解决二进制数中1的个数

&#x1f436;博主主页&#xff1a;ᰔᩚ. 一怀明月ꦿ ❤️‍&#x1f525;专栏系列&#xff1a;线性代数&#xff0c;C初学者入门训练 &#x1f525;座右铭&#xff1a;“不要等到什么都没有了&#xff0c;才下定决心去做” &#x1f680;&#x1f680;&#x1f680;大家觉不错…...

编程日记 2023/5/17 2:54:09

泛型详解.

1 泛型的引入 问题&#xff1a;我们之前实现过的顺序表&#xff0c;只能保存 int 类型的元素&#xff0c;如果现在需要保存 指向 Person 类型对象的引用的顺序表&#xff0c;请问应该如何解决&#xff1f;如果又需要保存指向 Book 对象类型的引用呢&#xff1f; 之前写的顺序表…...

编程日记 2023/5/17 2:54:07

Vue 3.0 响应性 深入响应性原理 【Vue3 从零开始】

现在是时候深入了&#xff01;Vue 最独特的特性之一&#xff0c;是其非侵入性的响应性系统。数据模型是被代理的 JavaScript 对象。而当你修改它们时&#xff0c;视图会进行更新。这让状态管理非常简单直观&#xff0c;不过理解其工作原理同样重要&#xff0c;这样你可以避开一…...

编程日记 2023/5/17 2:54:04

升级 vue3 常见问题总汇

Ⅰ、前言 虽然 vue3 是没有删除 vue2 的 选项式 API &#xff0c; 但是我们升级vue3 还是需要修改很多问题的下面来看看我们升级常见的一些问题 &#x1f447; 文章目录Ⅰ、前言Ⅱ、解决兼容问题1、路由的创建方式2、路由的方法变化3、升级 vuex 到 4.x4、作用域 插槽语法修改…...

编程日记 2023/5/17 2:54:02

汽车 Automotive ＞ T-BOX GNSS高精定位测试相关知识

参考&#xff1a;https://en.wikipedia.org/wiki/Global_Positioning_SystemGPS和GNSS的关系GPS&#xff08;Global Positioning System&#xff09;&#xff0c;全球定位系统是美国军民两用的导航定位卫星系统&#xff0c;GPS包含双频信号&#xff0c;频点L1、L2和L5GNSS&…...

编程日记 2023/5/16 6:43:12

大数据面试核心101问【大厂超级喜欢这些题】

之前出过《史上最全的大数据开发八股文》这篇文章&#xff0c;同学们都觉得还不错&#xff0c;但是有些同学觉得那个背起来还是有些吃力&#xff0c;于是我再次回顾了自己之前面试所有大厂的一些面试题以及牛客上面的一些面经&#xff0c;然后总结了频率问的最高的101问&#x…...

编程日记 2023/5/16 4:20:45

代码随想录算法训练营第四十八天 | leetcode 121. 买卖股票的最佳时机，122.买卖股票的最佳时机II

代码随想录算法训练营第四十八天 | leetcode 121. 买卖股票的最佳时机&#xff0c;122.买卖股票的最佳时机II121. 买卖股票的最佳时机122.买卖股票的最佳时机II121. 买卖股票的最佳时机 题目&#xff1a; 给定一个数组 prices &#xff0c;它的第 i 个元素 prices[i] 表示一支…...

编程日记 2023/5/17 2:54:00

HTML 列表、表格、表单

1 列表标签 作用&#xff1a;布局内容排列整齐的区域 列表分类&#xff1a;无序列表、有序列表、定义列表。 例如&#xff1a; 1.1 无序列表 标签&#xff1a;ul 嵌套 li&#xff0c;ul是无序列表&#xff0c;li是列表条目。 注意事项&#xff1a; ul 标签里面只能包裹 li…...

编程新知 2026/1/24 22:33:33

srs linux

下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935&#xff0c;SRS管理页面端口是8080&#xff0c;可…...

编程新知 2026/2/6 9:49:55

前端开发面试题总结-JavaScript篇(一)

文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包&#xff08;Closure&#xff09;&#xff1f;闭包有什么应用场景和潜在问题&#xff1f;2.解释 JavaScript 的作用域链&#xff08;Scope Chain&#xff09; 二、原型与继承3.原型链是什么&#xff1f;如何实现继承&a…...

编程新知 2026/2/1 3:12:03

Java线上CPU飙高问题排查全指南

一、引言 在Java应用的线上运行环境中&#xff0c;CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时&#xff0c;通常会导致应用响应缓慢&#xff0c;甚至服务不可用&#xff0c;严重影响用户体验和业务运行。因此&#xff0c;掌握一套科学有效的CPU飙高问题排查方法&…...

编程新知 2025/11/2 5:30:15

Caliper 配置文件解析：fisco-bcos.json

config.yaml 文件 config.yaml 是 Caliper 的主配置文件，通常包含以下内容： test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

编程新知 2025/10/24 15:14:02

Linux部署私有文件管理系统MinIO

最近需要用到一个文件管理服务&#xff0c;但是又不想花钱&#xff0c;所以就想着自己搭建一个&#xff0c;刚好我们用的一个开源框架已经集成了MinIO&#xff0c;所以就选了这个 我这边对文件服务性能要求不是太高&#xff0c;单机版就可以 安装非常简单&#xff0c;几个命令就…...

编程新知 2026/2/7 17:45:38

vue3 daterange正则踩坑

<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

编程新知 2025/12/27 19:12:09

自定义线程池1.2

自定义线程池 1.2 1. 简介 上次我们实现了 1.1 版本&#xff0c;将线程池中的线程数量交给使用者决定&#xff0c;并且将线程的创建延迟到任务提交的时候&#xff0c;在本文中我们将对这个版本进行如下的优化&#xff1a; 在新建线程时交给线程一个任务。让线程在某种情况下…...

编程新知 2026/1/11 0:26:20

dvwa11——XSS(Reflected)

LOW 分析源码&#xff1a;无过滤 和上一关一样&#xff0c;这一关在输入框内输入&#xff0c;成功回显 <script>alert(relee);</script> MEDIUM 分析源码&#xff0c;是把<script>替换成了空格&#xff0c;但没有禁用大写 改大写即可&#xff0c;注意函数…...

编程新知 2026/2/1 1:49:58

【SSM】SpringMVC学习笔记7：前后端数据传输协议和异常处理

这篇学习笔记是Spring系列笔记的第7篇&#xff0c;该笔记是笔者在学习黑马程序员SSM框架教程课程期间的笔记&#xff0c;供自己和他人参考。 Spring学习笔记目录 笔记1&#xff1a;【SSM】Spring基础&#xff1a; IoC配置学习笔记-CSDN博客 对应黑马课程P1~P20的内容。 笔记2…...

编程新知 2026/2/4 16:09:27