【课程作业】提取图中苹果的面积、周长和最小外接矩形的python、matlab和c++代码
提取图中苹果的面积、周长和最小外接矩形
在图像处理中,提取对象的关键属性是常见的任务之一。本文将演示如何使用三种流行的编程语言——Python、Matlab和C++,利用相应的图像处理库(OpenCV或Matlab内置函数)来提取图像中苹果的面积、周长和最小外接矩形。
问题描述
我们有一张包含苹果的图片,我们想要从这张图片中提取苹果的关键信息,包括:
- 苹果的面积(以像素为单位)。
- 苹果的周长(以像素为单位)。
- 苹果的最小外接矩形的位置和大小。
Python代码
import cv2# 读取图片
image = cv2.imread('apple_image.jpg')# 转换为灰度图像
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)# 使用阈值分割图像
_, binary = cv2.threshold(gray, 120, 255, cv2.THRESH_BINARY_INV)# 查找轮廓
contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)# 假设最大的轮廓为苹果
apple_contour = max(contours, key=cv2.contourArea)# 计算面积和周长
area = cv2.contourArea(apple_contour)
perimeter = cv2.arcLength(apple_contour, True)# 找到最小外接矩形
x, y, w, h = cv2.boundingRect(apple_contour)# 显示结果
print("Area:", area)
print("Perimeter:", perimeter)
print("Bounding Box:", (x, y, w, h))MATLAB代码
% 读取图片
image = imread('apple_image.jpg');% 转换为灰度图像
grayImage = rgb2gray(image);% 使用阈值分割图像
bwImage = imbinarize(grayImage);% 查找轮廓
contours = bwboundaries(bwImage);% 假设最大的轮廓为苹果
maxArea = 0;
for i = 1:length(contours)area = polyarea(contours{i}(:,2), contours{i}(:,1));if area > maxAreamaxArea = area;appleContour = contours{i};end
end% 计算面积和周长
appleArea = maxArea;
applePerimeter = sum(sqrt(sum(diff(appleContour).^2,2)));% 找到最小外接矩形
rect = regionprops(bwImage,'BoundingBox');
appleRect = rect.BoundingBox;% 显示结果
disp("Area:" + appleArea);
disp("Perimeter:" + applePerimeter);
disp("Bounding Box:" + appleRect);
c++代码
#include <opencv2/opencv.hpp>int main() {// 读取图片cv::Mat image = cv::imread("apple_image.jpg");// 转换为灰度图像cv::Mat gray;cv::cvtColor(image, gray, cv::COLOR_BGR2GRAY);// 使用阈值分割图像cv::Mat thresh;cv::threshold(gray, thresh, 120, 255, cv::THRESH_BINARY_INV);// 查找轮廓std::vector<std::vector<cv::Point>> contours;cv::findContours(thresh, contours, cv::RETR_EXTERNAL, cv::CHAIN_APPROX_SIMPLE);// 假设最大的轮廓为苹果double maxArea = 0;std::vector<cv::Point> appleContour;for (const auto& contour : contours) {double area = cv::contourArea(contour);if (area > maxArea) {maxArea = area;appleContour = contour;}}// 计算面积和周长double appleArea = maxArea;double applePerimeter = cv::arcLength(appleContour, true);// 找到最小外接矩形cv::Rect appleRect = cv::boundingRect(appleContour);// 显示结果std::cout << "Area: " << appleArea << std::endl;std::cout << "Perimeter: " << applePerimeter << std::endl;std::cout << "Bounding Box: " << appleRect << std::endl;return 0;
}相关文章:

【课程作业】提取图中苹果的面积、周长和最小外接矩形的python、matlab和c++代码
提取图中苹果的面积、周长和最小外接矩形 在图像处理中,提取对象的关键属性是常见的任务之一。本文将演示如何使用三种流行的编程语言——Python、Matlab和C,利用相应的图像处理库(OpenCV或Matlab内置函数)来提取图像中苹果的面积…...
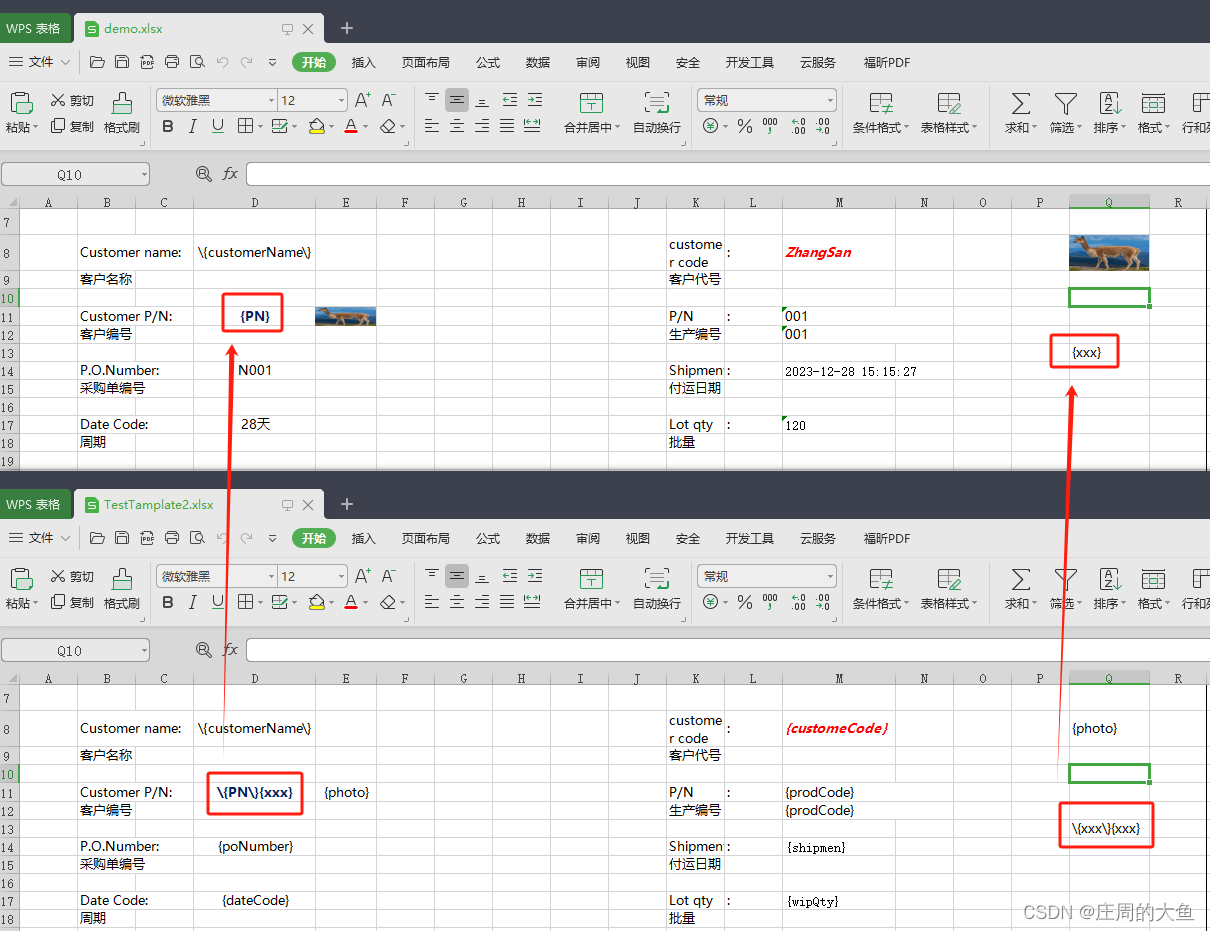
解决easyExcel模板填充时转义字符\{xxx\}失效
正常我们在使用easyExcel进行模板填充时,定义的变量会填充好对应的实际数据,未定义的变量会被清空,但是如果这个未定义的变量其实是模板的一部分,那么清空了就出错了。 在这张图里,上面的是模板填充后导出的文件&…...

在项目中使用CancelToken选择性取消Axios请求
Axios 提供了 CancelToken 类来创建取消标记。取消标记实际上是一个包含 token 标记和 cancel 方法的对象。 1、基本使用方法 const CancelToken axios.CancelToken; const source CancelToken.source();axios.get(/user/12345, {cancelToken: source.token }).catch(functi…...

[c++] 记录一次引用使用不当导致的 bug
在工作中看到了如下代码,代码基于 std::thread 封装了一个 Thread 类。Thread 封装了业务开发中常用的接口,比如设置调度策略,设置优先级,设置线程名。如下代码删去了不必要的代码,只保留能说明问题的代码。从代码实现…...

能不能节约百分之九十的算力来训练模型
Sora是由OpenAI开发的视频生成模型,它采用了多种先进的技术和架构,能够根据文本描述生成长达一分钟的高清视频。虽然OpenAI并未公开Sora的详细模型架构和实现细节,但我们可以根据公开的信息和参考论文来了解其技术架构。 Sora的核心技术架构主…...
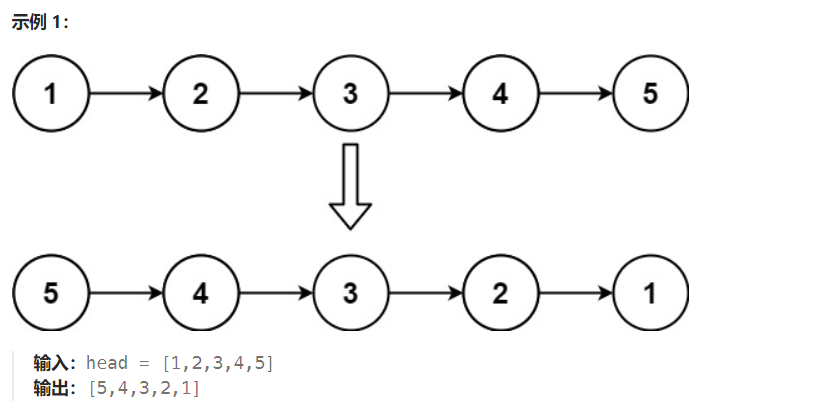
LeetCode206: 反转链表.
题目描述 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 解题方法 假设链表为 1→2→3→∅,我们想要把它改成∅←1←2←3。在遍历链表时,将当前节点的 next指针改为指向前一个节点。由于节点没有引用其前一…...

高级统计方法 第1次作业
概念 1. 请解释什么是P值,怎么计算p值,p值结果怎么理解,p值有哪些应用......? (a)什么是P值 P值是一种用来判定假设检验结果的一个参数,它描述了在原假设为真的情况下,比所得到的…...

spinalhdl,vivado,fpga
https://spinalhdl.github.io/SpinalDoc-RTD/master spinal hdl sudo apt install openjdk-17-jdk scala curl echo “deb https://repo.scala-sbt.org/scalasbt/debian all main” | sudo tee /etc/apt/sources.list.d/sbt.list echo “deb https://repo.scala-sbt.org/scal…...
)
Tomcat线程池原理(下篇:工作原理)
文章目录 前言正文一、执行线程的基本流程1.1 JUC中的线程池执行线程1.2 Tomcat 中线程池执行线程 二、被改造的阻塞队列2.1 TaskQueue的 offer(...)2.2 TaskQueue的 force(...) 三、总结 前言 Tomcat 线程池,是依据 JUC 中的线程池 ThreadPoolExecutor 重新自定义…...

【服务器数据恢复】通过reed-solomon算法恢复raid6数据的案例
服务器数据恢复环境: 一台网站服务器中有一组由6块磁盘组建的RAID6磁盘阵列,操作系统层面运行MySQL数据库和存放一些其他类型文件。 服务器故障: 该服务器在工作过程中,raid6磁盘阵列中有两块磁盘先后离线,不知道是管理…...

LeetCode 2583.二叉树中的第 K 大层和:层序遍历 + 排序
【LetMeFly】2583.二叉树中的第 K 大层和:层序遍历 排序 力扣题目链接:https://leetcode.cn/problems/kth-largest-sum-in-a-binary-tree/ 给你一棵二叉树的根节点 root 和一个正整数 k 。 树中的 层和 是指 同一层 上节点值的总和。 返回树中第 k …...

element ui 安装 简易过程 已解决
我之所以将Element归类为Vue.js,其主要原因是Element是(饿了么团队)基于MVVM框架Vue开源出来的一套前端ui组件。我最爱的就是它的布局容器!!! 下面进入正题: 1、Element的安装 首先你需要创建…...

websoket
WebSockets 是一种先进的技术。它可以在用户的浏览器和服务器之间打开交互式通信会话。你可以向服务器发送消息并接收事件驱动的响应,而无需通过轮询服务器的方式以获得响应,比较典型的应用场景就是即时通讯(聊天)系统。 <!DOC…...

案例:微服务从Java/SpringBoot迁移到Golan
基于 Java 的微服务,特别是那些使用 Spring Boot 的微服务,长期以来因其强大的功能和广泛的社区支持而闻名。Spring Boot 的约定优于配置方法简化了微服务的部署和开发,提供了大量开箱即用的功能,例如自动配置、独立功能和简单的依…...

小波变换模拟
小波变换是一种信号处理技术,通过在时间-频率域中使用基于小波的函数进行信号分析。小波变换在处理非平稳信号和图像时特别有用,可以将信号分解为不同频率的成分。它在数据压缩、去噪、特征提取等领域有广泛应用。 MATLAB中提供了用于二维离散小波变换的…...

cv::Mat图像操作
图像读写 //include header #include <opencv2/imgcodecs.hpp>/** Currently, the following file formats are supported: Windows bitmaps - *.bmp, *.dib (always supported) JPEG files - *.jpeg, *.jpg, *.jpe (see the Note section) JPEG 2000 files - *.jp2 (s…...

【机器学习基础】一元线性回归(适合初学者的保姆级文章)
🚀个人主页:为梦而生~ 关注我一起学习吧! 💡专栏:机器学习 欢迎订阅!后面的内容会越来越有意思~ 💡往期推荐: 【机器学习基础】机器学习入门(1) 【机器学习基…...

2024年软件测试岗位-面试
第一部分: 1、自我介绍:简历写到的快速描述,学校、学历、工作经验等(注意:不要过度优化简历,你不写别人可能会问,但你写了别人一定会问!) 第二部分: 1、功能测…...

【坑】Spring Boot整合MyBatis,一级缓存失效
一、Spring Boot整合MyBatis,一级缓存失效 1.1、概述 MyBatis一级缓存的作用域是同一个SqlSession,在同一个SqlSession中执行两次相同的查询,第一次执行完毕后,Mybatis会将查询到的数据缓存起来(缓存到内存中…...
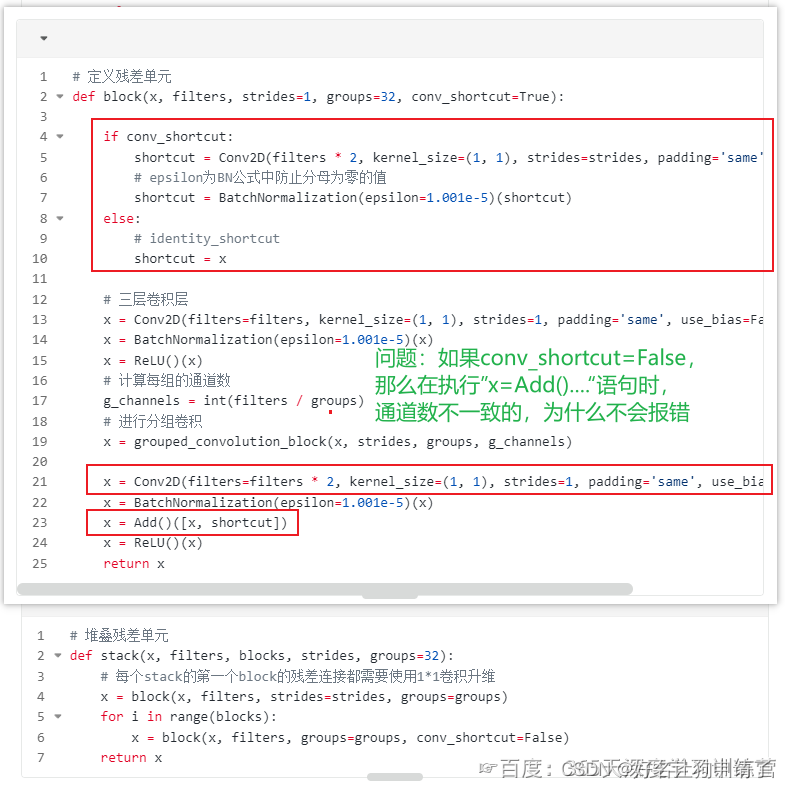
J7 - 对于ResNeXt-50算法的思考
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 | 接辅导、项目定制 J6周有一段代码如下 思考过程 首先看到这个问题的描述,想到的是可能使用了向量操作的广播机制然后就想想办法验证一下&…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...
