【MATLAB】 EWT信号分解+FFT傅里叶频谱变换组合算法
有意向获取代码,请转文末观看代码获取方式~
展示出图效果


1 EWT分解算法
EWT分解算法是一种基于小波变换的信号分解算法,它可以将信号分解为一系列具有不同频率特性的小波分量。该算法的基本思想是将信号分解为多个不同尺度的小波分量,并对每个小波分量进行频域分析。
EWT分解算法具有以下优点:
-
具有良好的频率局部特性,能够准确地提取信号的频率信息。
-
能够适应各种类型的信号,具有较好的通用性。
-
能够有效地处理高频信号,对于突变信号有较好的适应性。
-
能够避免小波变换中的吉布斯现象,对于信号的细节信息有较好的保留。
在应用方面,EWT分解算法可以应用于信号处理、图像处理、地震信号处理等领域,是一种有效的信号分析方法。
MATLAB 信号分解第十期-EWT 分解:
信号分解全家桶详情请参见:
2 FFT傅里叶频谱变换算法
傅里叶变换是一种数学方法,用于将一个信号分解成一系列正弦和余弦函数的和,从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用,包括音频处理、图像处理等。 具体来说,傅里叶变换的步骤如下:
-
给定一个连续时间域函数f(t),其中t为时间。
-
对f(t)进行傅里叶变换,得到它的频率域表示F(ω),其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和,即: F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中,k为频率分量的序号,a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号,从而更好地理解信号的频率分量和周期性特征,同时也方便进行一些信号处理任务,例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理,计算量较大,在实时处理等场景下可能会存在较大的延迟。
MATLAB | 频谱分析算法 | 傅里叶变换 开源 MATLAB 代码请转:
MATLAB | 9种频谱分析算法全家桶详情请参见:
3 EWT信号分解+FFT傅里叶频谱变换组合算法
如下为简短的视频操作教程。
【MATLAB 】 EWT信号分解+FFT傅里叶频谱变换组合算法请转:
【MATLAB 】信号分解+FFT傅里叶频谱变换组合算法全家桶详情请参见:
关于代码有任何疑问,可以一起探讨科研,写作,代码等诸多学术问题,我们一起进步~
代码见附件
相关文章:

【MATLAB】 EWT信号分解+FFT傅里叶频谱变换组合算法
有意向获取代码,请转文末观看代码获取方式~ 展示出图效果 1 EWT分解算法 EWT分解算法是一种基于小波变换的信号分解算法,它可以将信号分解为一系列具有不同频率特性的小波分量。该算法的基本思想是将信号分解为多个不同尺度的小波分量,并对…...

MATLAB中,如何捕获和处理异常?如何在MATLAB中自定义错误消息?在MATLAB中,error函数和warning函数有什么区别?
MATLAB中,如何捕获和处理异常? 在MATLAB中,捕获和处理异常通常使用try-catch语句。try块包含可能引发异常的代码,而catch块则包含当异常发生时执行的代码。以下是如何在MATLAB中捕获和处理异常的基本步骤: 使用try关键…...
【算法与数据结构】127、LeetCode单词接龙
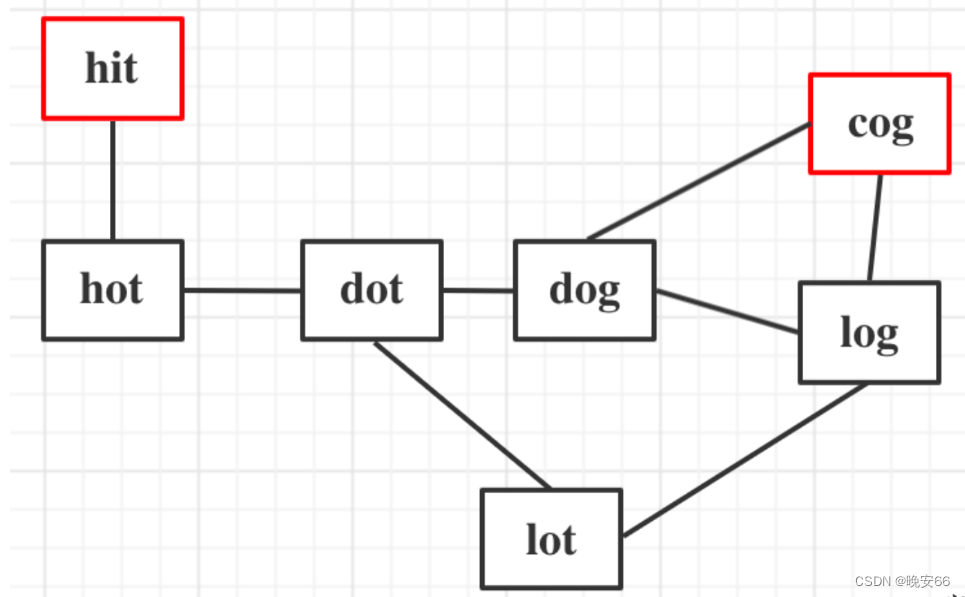
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:示例1为例,hit到达cog的路线不止一条,如何找到最短是关键。广度优先搜索是一圈…...

CAN——创建一个数据库DBC文件
一、创建一个工程 file——new——can 500kbaud1ch 得到一个工程文件.cfg 二、实现两个节点通讯 can networks 三、创建数据库DBC tool——candbeditor——file——creatdatabase——cantemplate.dbc 1.建数值表 view——value tables——空白处右击add—— definition 定…...

(十三)【Jmeter】线程(Threads(Users))之tearDown 线程组
简述 操作路径如下: 作用:在正式测试结束后执行清理操作,如关闭连接、释放资源等。配置:设置清理操作的采样器、执行顺序等参数。使用场景:确保在测试结束后应用程序恢复到正常状态,避免资源泄漏或对其他测试的影响。优点:提供清理操作,确保测试环境的整洁和可重复性…...
MySQL数据库基础(十三):关系型数据库三范式介绍
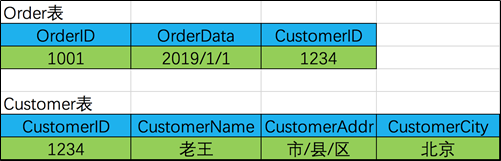
文章目录 关系型数据库三范式介绍 一、什么是三范式 二、数据冗余 三、范式的划分 四、一范式 五、二范式 六、三范式 七、总结 关系型数据库三范式介绍 一、什么是三范式 设计关系数据库时,遵从不同的规范要求,设计出合理的关系型数据库&…...
的力量与挑战)
掌控互联网脉络:深入解析边界网关协议(BGP)的力量与挑战
BGP简介 边界网关协议(Border Gateway Protocol,BGP)是互联网上最重要的路由协议之一,负责在不同自治系统(AS)之间传播路由信息。BGP使得互联网中的不同网络可以互相通信,支持互联网的规模化扩…...

Vue2页面转化为Vue3
vue2element-ui转化为Vue3element plus 后台管理系统:增删查改 vue2页面: <template><div class"app-container"><div><el-form:model"queryParams"ref"queryForm"size"small":inline&qu…...

【课程作业】提取图中苹果的面积、周长和最小外接矩形的python、matlab和c++代码
提取图中苹果的面积、周长和最小外接矩形 在图像处理中,提取对象的关键属性是常见的任务之一。本文将演示如何使用三种流行的编程语言——Python、Matlab和C,利用相应的图像处理库(OpenCV或Matlab内置函数)来提取图像中苹果的面积…...
解决easyExcel模板填充时转义字符\{xxx\}失效
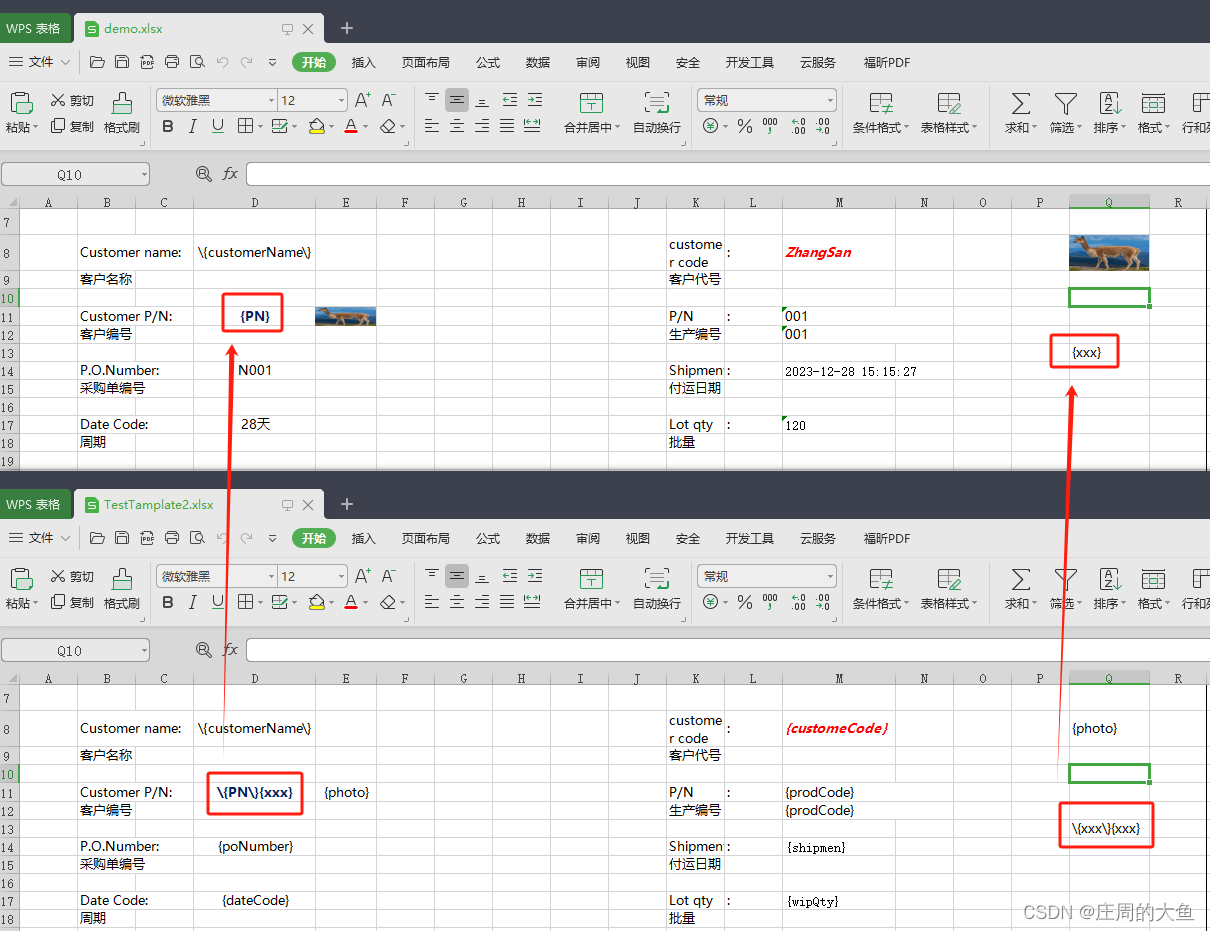
正常我们在使用easyExcel进行模板填充时,定义的变量会填充好对应的实际数据,未定义的变量会被清空,但是如果这个未定义的变量其实是模板的一部分,那么清空了就出错了。 在这张图里,上面的是模板填充后导出的文件&…...

在项目中使用CancelToken选择性取消Axios请求
Axios 提供了 CancelToken 类来创建取消标记。取消标记实际上是一个包含 token 标记和 cancel 方法的对象。 1、基本使用方法 const CancelToken axios.CancelToken; const source CancelToken.source();axios.get(/user/12345, {cancelToken: source.token }).catch(functi…...

[c++] 记录一次引用使用不当导致的 bug
在工作中看到了如下代码,代码基于 std::thread 封装了一个 Thread 类。Thread 封装了业务开发中常用的接口,比如设置调度策略,设置优先级,设置线程名。如下代码删去了不必要的代码,只保留能说明问题的代码。从代码实现…...

能不能节约百分之九十的算力来训练模型
Sora是由OpenAI开发的视频生成模型,它采用了多种先进的技术和架构,能够根据文本描述生成长达一分钟的高清视频。虽然OpenAI并未公开Sora的详细模型架构和实现细节,但我们可以根据公开的信息和参考论文来了解其技术架构。 Sora的核心技术架构主…...
LeetCode206: 反转链表.
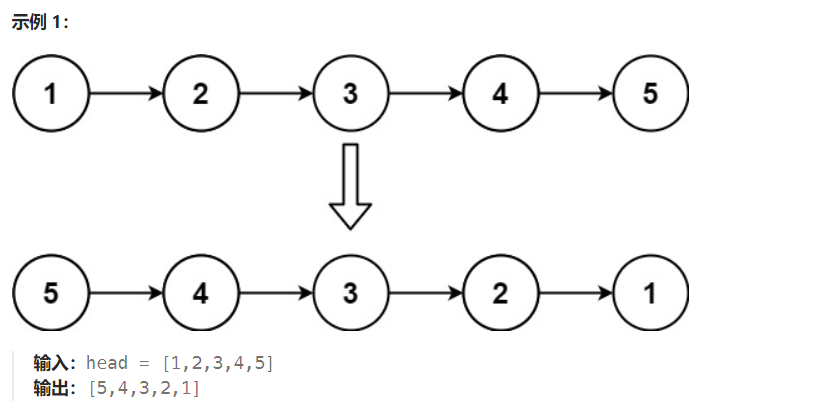
题目描述 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 解题方法 假设链表为 1→2→3→∅,我们想要把它改成∅←1←2←3。在遍历链表时,将当前节点的 next指针改为指向前一个节点。由于节点没有引用其前一…...

高级统计方法 第1次作业
概念 1. 请解释什么是P值,怎么计算p值,p值结果怎么理解,p值有哪些应用......? (a)什么是P值 P值是一种用来判定假设检验结果的一个参数,它描述了在原假设为真的情况下,比所得到的…...

spinalhdl,vivado,fpga
https://spinalhdl.github.io/SpinalDoc-RTD/master spinal hdl sudo apt install openjdk-17-jdk scala curl echo “deb https://repo.scala-sbt.org/scalasbt/debian all main” | sudo tee /etc/apt/sources.list.d/sbt.list echo “deb https://repo.scala-sbt.org/scal…...
)
Tomcat线程池原理(下篇:工作原理)
文章目录 前言正文一、执行线程的基本流程1.1 JUC中的线程池执行线程1.2 Tomcat 中线程池执行线程 二、被改造的阻塞队列2.1 TaskQueue的 offer(...)2.2 TaskQueue的 force(...) 三、总结 前言 Tomcat 线程池,是依据 JUC 中的线程池 ThreadPoolExecutor 重新自定义…...

【服务器数据恢复】通过reed-solomon算法恢复raid6数据的案例
服务器数据恢复环境: 一台网站服务器中有一组由6块磁盘组建的RAID6磁盘阵列,操作系统层面运行MySQL数据库和存放一些其他类型文件。 服务器故障: 该服务器在工作过程中,raid6磁盘阵列中有两块磁盘先后离线,不知道是管理…...

LeetCode 2583.二叉树中的第 K 大层和:层序遍历 + 排序
【LetMeFly】2583.二叉树中的第 K 大层和:层序遍历 排序 力扣题目链接:https://leetcode.cn/problems/kth-largest-sum-in-a-binary-tree/ 给你一棵二叉树的根节点 root 和一个正整数 k 。 树中的 层和 是指 同一层 上节点值的总和。 返回树中第 k …...

element ui 安装 简易过程 已解决
我之所以将Element归类为Vue.js,其主要原因是Element是(饿了么团队)基于MVVM框架Vue开源出来的一套前端ui组件。我最爱的就是它的布局容器!!! 下面进入正题: 1、Element的安装 首先你需要创建…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
