备战蓝桥杯————递归反转单链表的一部分
递归反转单链表已经明白了,递归反转单链表的一部分你知道怎么做吗?
一、反转链表Ⅱ
题目描述
给你单链表的头指针
head和两个整数left和right,其中left <= right。请你反转从位置left到位置right的链表节点,返回 反转后的链表 。
示例 1:
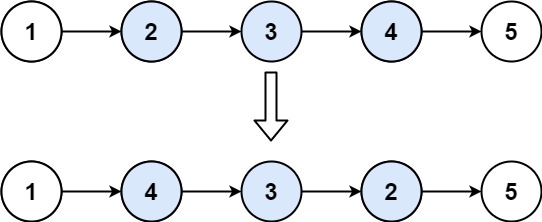
输入:head = [1,2,3,4,5], left = 2, right = 4 输出:[1,4,3,2,5]
示例 2:
输入:head = [5], left = 1, right = 1 输出:[5]
提示:
- 链表中节点数目为
n 1 <= n <= 500-500 <= Node.val <= 5001 <= left <= right <= n
进阶: 你可以使用一趟扫描完成反转吗?
解题思路及代码
reverseN 递归反转链表的算法,具体的思路如下:
- 函数 reverseN 用于反转以 head 为起点的前 n 个节点,并返回反转后的新头结点。
- 当 n 等于 1 时,表示只有一个节点需要反转,那么记录下第 n + 1 个节点(后驱节点 successor),并返回当前节点 head。
- 当 n 大于 1 时,递归调用 reverseN 函数反转前 n - 1 个节点,得到反转后的新头结点 last。
- 在反转的过程中,将 head 的下一个节点 head.next 的 next 指针指向 head,实现反转。
- 将 head 的 next 指针指向记录的后驱节点 successor,保证反转后的链表与后面的节点连接起来。
- 返回新的头结点 last,作为上一层递归的结果。
- 当 m 不等于 1 时,我们需要将 head 的索引视为 1,并且进行递归处理。此时,我们希望从第 m 个元素开始反转。因此,我们需要将 head.next 的索引视为 1,然后递归地处理head.next,将范围调整为从第 m - 1 个元素开始反转。
- 具体来说,对于 head.next.next,我们需要将 head.next.next 的索引视为 1。这意味着我们希望从 head.next.next 开始反转。因此,我们将递归地调用 reverseBetween 方法,并将 head.next.next 作为新的头结点,范围调整为从第 m - 2 个元素开始反转。
- 通过不断地将头结点向后移动,并调整范围,我们可以确保在链表中正确地定位到需要反转的范围,并对其进行处理。这样,无论 m 的值是多少,我们都能在链表中正确地找到需要反转的区间。
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode reverseBetween(ListNode head, int left, int right) {if(left==1){return reverseN(head,right);}head.next=reverseBetween(head.next,left-1,right-1);return head;}ListNode succetor=null;public ListNode reverseN(ListNode head, int n){if(n==1){succetor=head.next;return head;}ListNode last=reverseN(head.next,n-1);head.next.next=head;head.next=succetor;return last;}
}结果展示
相关文章:

备战蓝桥杯————递归反转单链表的一部分
递归反转单链表已经明白了,递归反转单链表的一部分你知道怎么做吗? 一、反转链表Ⅱ 题目描述 给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反…...

rabbitmq知识梳理
一.WorkQueues模型 Work queues,任务模型。简单来说就是让多个消费者绑定到一个队列,共同消费队列中的消息。 当消息处理比较耗时的时候,可能生产消息的速度会远远大于消息的消费速度。长此以往,消息就会堆积越来越多,…...

【数据结构与算法】动态规划法解题20240227
动态规划法 一、什么是动态规划二、动态规划的解题步骤三、509. 斐波那契数1、动规五部曲: 四、70. 爬楼梯1、动规五部曲: 五、746. 使用最小花费爬楼梯1、动规五部曲: 一、什么是动态规划 动态规划,英文:Dynamic Pro…...
备战蓝桥杯—— 双指针技巧巧答链表2
对于单链表相关的问题,双指针技巧是一种非常广泛且有效的解决方法。以下是一些常见问题以及使用双指针技巧解决: 合并两个有序链表: 使用两个指针分别指向两个链表的头部,逐一比较节点的值,将较小的节点链接到结果链表…...

半监督节点分类-graph learning
半监督节点分类相当于在一个图当中,用一部分节点的类别上已知的,有另外一部分节点的类别是未知的,目标是使用有标签的节点来推断没有标签的节点 注意 半监督节点分类属于直推式学习,直推式学习相当于出现新节点后,需要…...
软件文档-运维-开发-管理-资质-评审-招投标-验收
开发文档:这类文档主要用于记录软件的开发过程和细节,包括: 《功能要求》:描述了软件应具备的功能,是软件开发的基础。《投标方案》:向潜在的客户或招标方展示公司的技术和项目实施能力。《需求分析》&…...

猫头虎分享已解决Bug || Vue中的TypeError: Cannot read property ‘name‘ of undefined 错误
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...

技术应用:使用Spring Boot、MyBatis Plus和Dynamic DataSource实现多数据源
引言 在现代的软件开发中,许多应用程序需要同时访问多个数据库。例如,一个电子商务平台可能需要访问多个数据库来存储用户信息、产品信息和订单信息等。在这种情况下,使用多数据源是一种常见的解决方案,它允许我们在一个应用程序…...
C# Onnx 使用onnxruntime部署实时视频帧插值
目录 介绍 效果 模型信息 项目 代码 下载 C# Onnx 使用onnxruntime部署实时视频帧插值 介绍 github地址:https://github.com/google-research/frame-interpolation FILM: Frame Interpolation for Large Motion, In ECCV 2022. The official Tensorflow 2…...

编程笔记 Golang基础 016 数据类型:数字类型
编程笔记 Golang基础 016 数据类型:数字类型 1. 整数类型(Integer Types)a) 固定长度整数:b) 变长整数: 2. 浮点数类型(Floating-Point Types)3. 复数类型(Complex Number Types&…...
一周学会Django5 Python Web开发-会话管理(CookiesSession)
锋哥原创的Python Web开发 Django5视频教程: 2024版 Django5 Python web开发 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili2024版 Django5 Python web开发 视频教程(无废话版) 玩命更新中~共计26条视频,包括:2024版 Django5 Python we…...

QT之QString.arg输出固定位数
问题描述 我需要用QString输出一个固定位数的数字字符串。起初我的代码是这样: int img_num 1 auto new_name QString("%1.png").arg((int)img_num, 3, 10, 0); //最后一个参数用u0也是一样的 qDebug() << "new_name:" << new…...

Linux下各种压缩包的压缩与解压
tar 归档,不压缩,常见后缀 .tar # 将文件夹归档成为一个包 tar cf rootfs.tar rootfs # 将归档包还原为文件夹 tar xf rootfs.tar # 将归档包还原到路径 a/b/c tar xf rootfs.tar -C a/b/cgzip压缩, 常见后缀 .tar.gz .tgz # 压缩 tar czf …...
【ctfshow—web】——信息搜集篇1(web1~20详解)
ctfshow—web题解 web1web2web3web4web5web6web7web8web9web10web11web12web13web14web15web16web17web18web19web20 web1 题目提示 开发注释未及时删除 那就找开发注释咯,可以用F12来查看,也可以CtrlU直接查看源代码呢 就拿到flag了 web2 题目提示 j…...
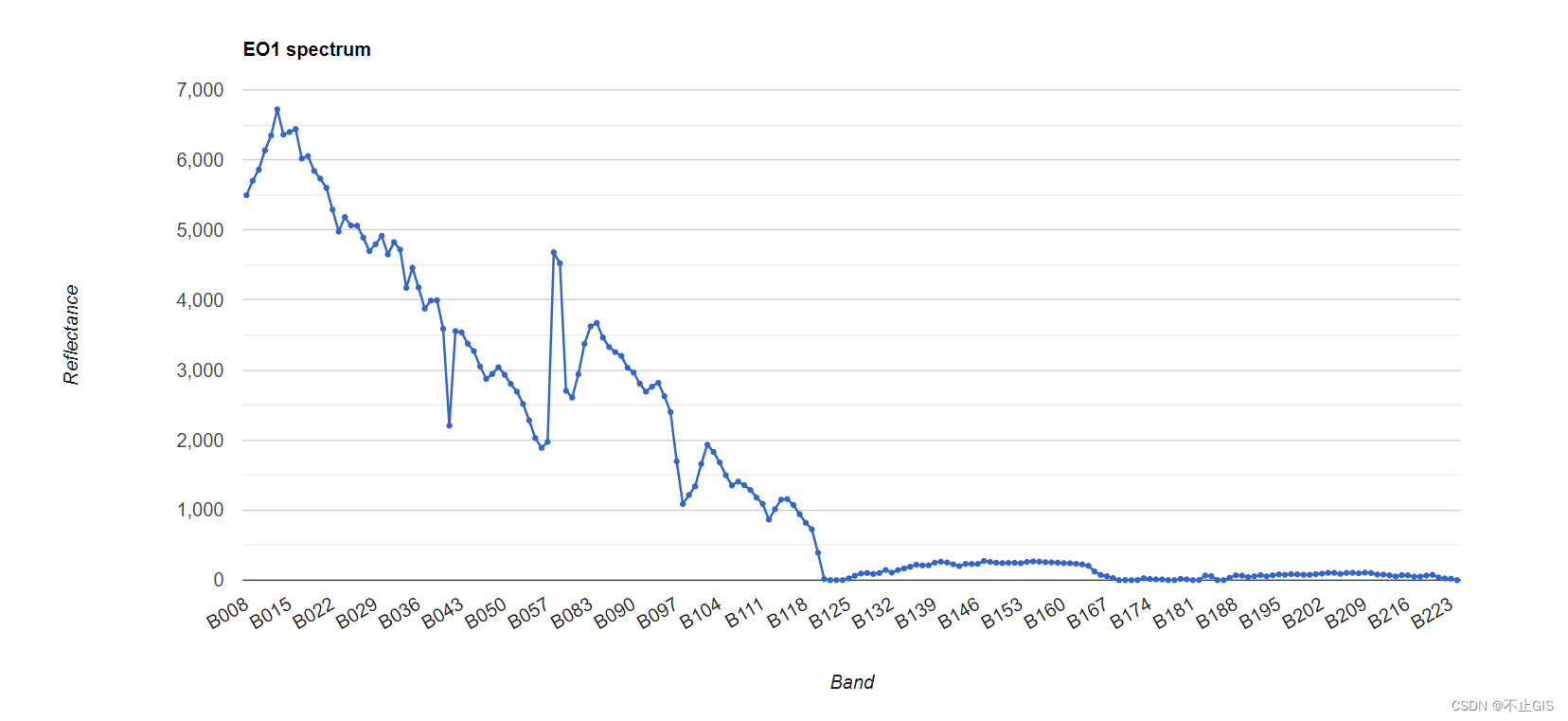
GEE入门篇|遥感专业术语(实践操作4):光谱分辨率(Spectral Resolution)
目录 光谱分辨率(Spectral Resolution) 1.MODIS 2.EO-1 光谱分辨率(Spectral Resolution) 光谱分辨率是指传感器进行测量的光谱带的数量和宽度。 您可以将光谱带的宽度视为每个波段的波长间隔,在多个波段测量辐射亮…...

c++中模板的注意事项
1. 模板定义时,<>中的虚拟类型参数不能为空。(因为我们使用模板就是希望使用模拟类型代替其它的类型,如果我们不定义就没有意义了) 2. 无论是定义函数模板还是类模板,其实template定义与后面使用虚拟类型的类或者函数,是…...
【代码随想录python笔记整理】第十三课 · 链表的基础操作 1
前言:本笔记仅仅只是对内容的整理和自行消化,并不是完整内容,如有侵权,联系立删。 一、链表 在之前的学习中,我们接触到了字符串和数组(列表)这两种结构,它们具有着以下的共同点:1、元素按照一定的顺序来排列。2、可以通过索引来访问数组中的元素和字符串中的字符。由此,…...
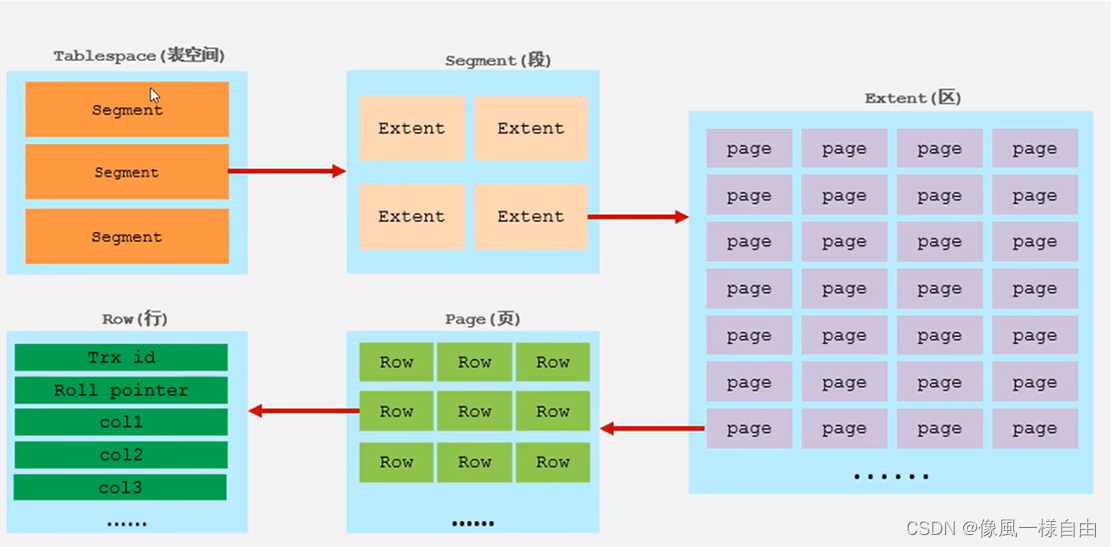
JAVA工程师面试专题-《Mysql》篇
目录 一、基础 1、mysql可以使用多少列创建索引? 2、mysql常用的存储引擎有哪些 3、MySQL 存储引擎,两者区别 4、mysql默认的隔离级别 5、数据库三范式 6、drop、delete 与 truncate 区别? 7、IN与EXISTS的区别 二、索引 1、索引及索…...
|Day22(二叉树))
@ 代码随想录算法训练营第4周(C语言)|Day22(二叉树)
代码随想录算法训练营第4周(C语言)|Day22(二叉树) Day22、二叉树(包含题目 ● 235. 二叉搜索树的最近公共祖先 ● 701.二叉搜索树中的插入操作 ● 450.删除二叉搜索树中的节点 ) 235. 二叉搜索树的最近公…...

福特锐界2021plus 汽车保养手册
福特锐界2021plus汽车保养手册两页,零部件保养要求,电子版放这里方便查询:...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...

P10909 [蓝桥杯 2024 国 B] 立定跳远
# P10909 [蓝桥杯 2024 国 B] 立定跳远 ## 题目描述 在运动会上,小明从数轴的原点开始向正方向立定跳远。项目设置了 $n$ 个检查点 $a_1, a_2, \cdots , a_n$ 且 $a_i \ge a_{i−1} > 0$。小明必须先后跳跃到每个检查点上且只能跳跃到检查点上。同时࿰…...
