用Python实现创建十二星座数据分析图表
下面小编提供的代码中,您已经将pie.render()注释掉,并使用了pie.render_to_file('十二星座.svg')来将饼状图渲染到一个名为十二星座.svg的文件中。这是一个正确的做法,如果您想在文件中保存图表而不是在浏览器中显示它。
成功创建图表:
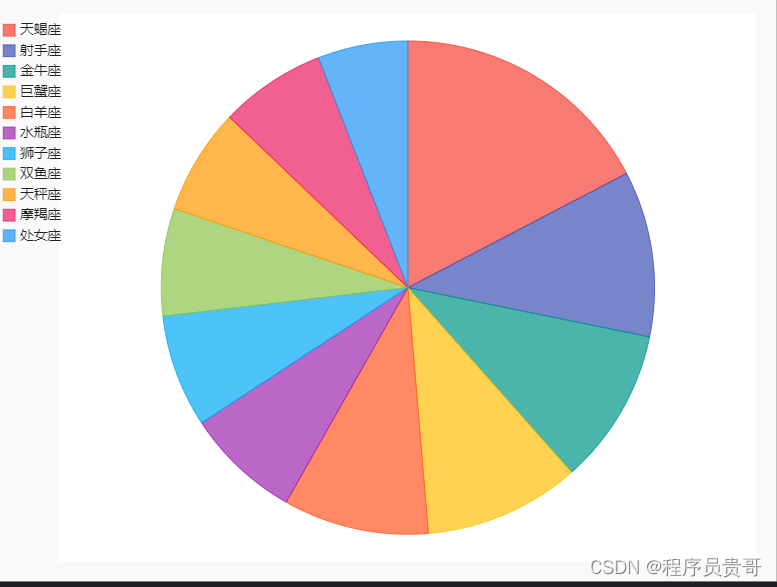
问题分析:
要确保代码能够正常工作并生成SVG文件,您可以按照以下步骤操作:
- 确保环境配置正确:
- 确保您的Python环境已经安装并配置好。
- 使用
pip安装pygal库:pip install pygal。
- 运行代码:
- 打开命令行或终端。
- 导航到包含您的Python脚本的目录。
- 运行脚本,例如如果您的脚本名为
zodiac_population.py,则运行python zodiac_population.py。
- 检查输出:
- 脚本执行后,您应该在脚本所在的目录中看到一个名为
十二星座.svg的文件。 - 使用Web浏览器或任何能够打开SVG文件的程序打开这个文件,您应该能够看到饼状图。
- 脚本执行后,您应该在脚本所在的目录中看到一个名为
如果您在执行这些步骤后仍然遇到问题,请检查以下几点:
- 文件权限:确保您有权限在脚本所在的目录中创建文件。
- 错误消息:如果命令行输出中显示任何错误消息,请仔细阅读并理解这些消息,它们可能会提供关于问题所在的线索。
- Python和pygal版本:确保您安装的Python和pygal库是最新的,或者至少是兼容的版本。
如果您遵循了这些步骤并且仍然无法生成SVG文件,请提供任何错误消息或异常信息,这样我可以进一步帮助您解决问题。
实现创建十二星座的图表的数据分析代码:
import pygal
pie = pygal.Pie()
pie_title = "中国各星座人口比例"
pie.add("天蝎座",15.74)
pie.add("射手座",9.86)
pie.add("金牛座",9.31)
pie.add("巨蟹座",9.27)
pie.add("白羊座",8.66)
pie.add("水瓶座",6.85)
pie.add("狮子座",6.70)
pie.add("双鱼座",6.40)
pie.add("天秤座",6.31)
pie.add("摩羯座",6.31)
pie.add("处女座",5.36)
#pie.render()
pie.render_to_file('十二星座.svg')小编推荐Pythont教程网:blog.pythonit.cn
相关文章:

用Python实现创建十二星座数据分析图表
下面小编提供的代码中,您已经将pie.render()注释掉,并使用了pie.render_to_file(十二星座.svg)来将饼状图渲染到一个名为十二星座.svg的文件中。这是一个正确的做法,如果您想在文件中保存图表而不是在浏览器中显示它。 成功创建图表…...
备战蓝桥杯————递归反转单链表的一部分
递归反转单链表已经明白了,递归反转单链表的一部分你知道怎么做吗? 一、反转链表Ⅱ 题目描述 给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反…...

rabbitmq知识梳理
一.WorkQueues模型 Work queues,任务模型。简单来说就是让多个消费者绑定到一个队列,共同消费队列中的消息。 当消息处理比较耗时的时候,可能生产消息的速度会远远大于消息的消费速度。长此以往,消息就会堆积越来越多,…...

【数据结构与算法】动态规划法解题20240227
动态规划法 一、什么是动态规划二、动态规划的解题步骤三、509. 斐波那契数1、动规五部曲: 四、70. 爬楼梯1、动规五部曲: 五、746. 使用最小花费爬楼梯1、动规五部曲: 一、什么是动态规划 动态规划,英文:Dynamic Pro…...
备战蓝桥杯—— 双指针技巧巧答链表2
对于单链表相关的问题,双指针技巧是一种非常广泛且有效的解决方法。以下是一些常见问题以及使用双指针技巧解决: 合并两个有序链表: 使用两个指针分别指向两个链表的头部,逐一比较节点的值,将较小的节点链接到结果链表…...

半监督节点分类-graph learning
半监督节点分类相当于在一个图当中,用一部分节点的类别上已知的,有另外一部分节点的类别是未知的,目标是使用有标签的节点来推断没有标签的节点 注意 半监督节点分类属于直推式学习,直推式学习相当于出现新节点后,需要…...
软件文档-运维-开发-管理-资质-评审-招投标-验收
开发文档:这类文档主要用于记录软件的开发过程和细节,包括: 《功能要求》:描述了软件应具备的功能,是软件开发的基础。《投标方案》:向潜在的客户或招标方展示公司的技术和项目实施能力。《需求分析》&…...

猫头虎分享已解决Bug || Vue中的TypeError: Cannot read property ‘name‘ of undefined 错误
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...

技术应用:使用Spring Boot、MyBatis Plus和Dynamic DataSource实现多数据源
引言 在现代的软件开发中,许多应用程序需要同时访问多个数据库。例如,一个电子商务平台可能需要访问多个数据库来存储用户信息、产品信息和订单信息等。在这种情况下,使用多数据源是一种常见的解决方案,它允许我们在一个应用程序…...
C# Onnx 使用onnxruntime部署实时视频帧插值
目录 介绍 效果 模型信息 项目 代码 下载 C# Onnx 使用onnxruntime部署实时视频帧插值 介绍 github地址:https://github.com/google-research/frame-interpolation FILM: Frame Interpolation for Large Motion, In ECCV 2022. The official Tensorflow 2…...

编程笔记 Golang基础 016 数据类型:数字类型
编程笔记 Golang基础 016 数据类型:数字类型 1. 整数类型(Integer Types)a) 固定长度整数:b) 变长整数: 2. 浮点数类型(Floating-Point Types)3. 复数类型(Complex Number Types&…...
一周学会Django5 Python Web开发-会话管理(CookiesSession)
锋哥原创的Python Web开发 Django5视频教程: 2024版 Django5 Python web开发 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili2024版 Django5 Python web开发 视频教程(无废话版) 玩命更新中~共计26条视频,包括:2024版 Django5 Python we…...

QT之QString.arg输出固定位数
问题描述 我需要用QString输出一个固定位数的数字字符串。起初我的代码是这样: int img_num 1 auto new_name QString("%1.png").arg((int)img_num, 3, 10, 0); //最后一个参数用u0也是一样的 qDebug() << "new_name:" << new…...

Linux下各种压缩包的压缩与解压
tar 归档,不压缩,常见后缀 .tar # 将文件夹归档成为一个包 tar cf rootfs.tar rootfs # 将归档包还原为文件夹 tar xf rootfs.tar # 将归档包还原到路径 a/b/c tar xf rootfs.tar -C a/b/cgzip压缩, 常见后缀 .tar.gz .tgz # 压缩 tar czf …...
【ctfshow—web】——信息搜集篇1(web1~20详解)
ctfshow—web题解 web1web2web3web4web5web6web7web8web9web10web11web12web13web14web15web16web17web18web19web20 web1 题目提示 开发注释未及时删除 那就找开发注释咯,可以用F12来查看,也可以CtrlU直接查看源代码呢 就拿到flag了 web2 题目提示 j…...
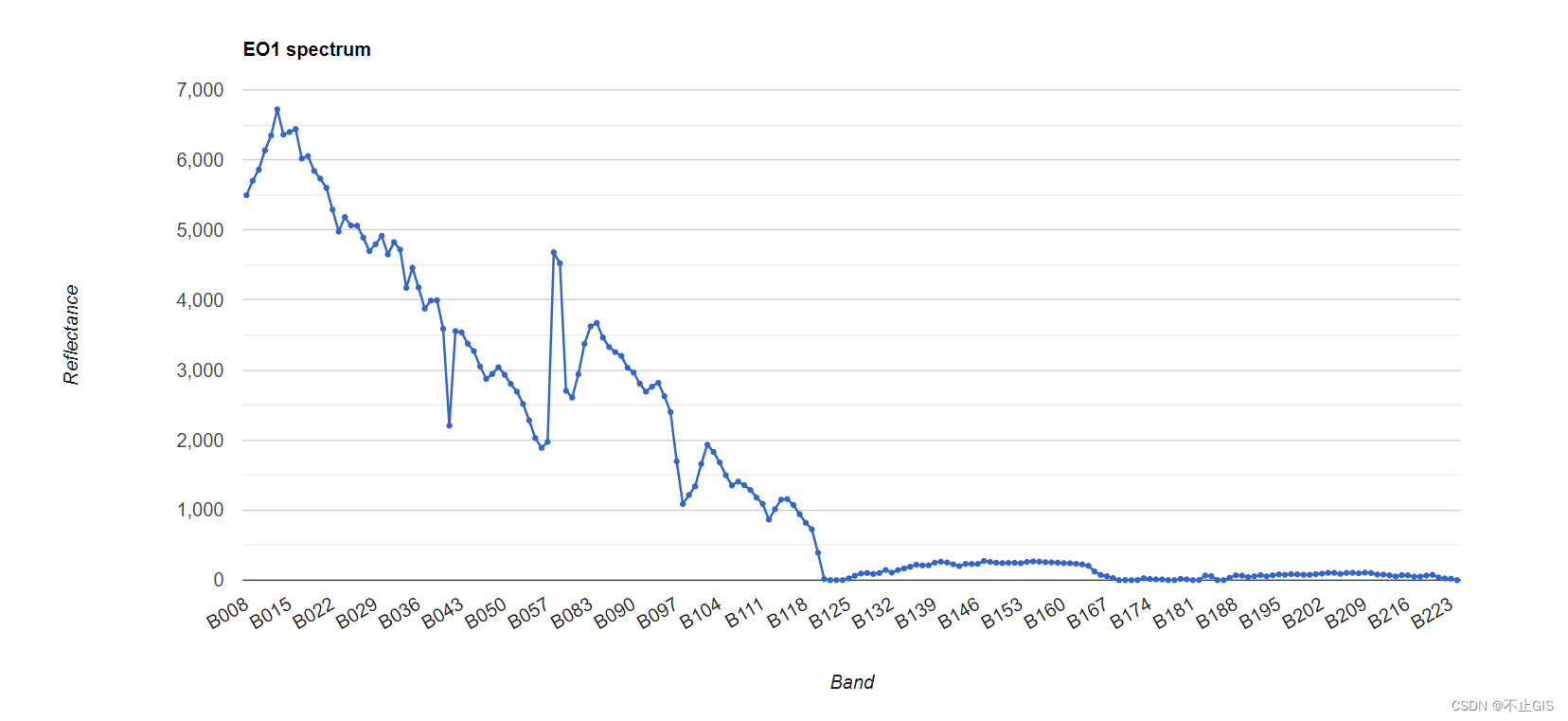
GEE入门篇|遥感专业术语(实践操作4):光谱分辨率(Spectral Resolution)
目录 光谱分辨率(Spectral Resolution) 1.MODIS 2.EO-1 光谱分辨率(Spectral Resolution) 光谱分辨率是指传感器进行测量的光谱带的数量和宽度。 您可以将光谱带的宽度视为每个波段的波长间隔,在多个波段测量辐射亮…...

c++中模板的注意事项
1. 模板定义时,<>中的虚拟类型参数不能为空。(因为我们使用模板就是希望使用模拟类型代替其它的类型,如果我们不定义就没有意义了) 2. 无论是定义函数模板还是类模板,其实template定义与后面使用虚拟类型的类或者函数,是…...
【代码随想录python笔记整理】第十三课 · 链表的基础操作 1
前言:本笔记仅仅只是对内容的整理和自行消化,并不是完整内容,如有侵权,联系立删。 一、链表 在之前的学习中,我们接触到了字符串和数组(列表)这两种结构,它们具有着以下的共同点:1、元素按照一定的顺序来排列。2、可以通过索引来访问数组中的元素和字符串中的字符。由此,…...
JAVA工程师面试专题-《Mysql》篇
目录 一、基础 1、mysql可以使用多少列创建索引? 2、mysql常用的存储引擎有哪些 3、MySQL 存储引擎,两者区别 4、mysql默认的隔离级别 5、数据库三范式 6、drop、delete 与 truncate 区别? 7、IN与EXISTS的区别 二、索引 1、索引及索…...
|Day22(二叉树))
@ 代码随想录算法训练营第4周(C语言)|Day22(二叉树)
代码随想录算法训练营第4周(C语言)|Day22(二叉树) Day22、二叉树(包含题目 ● 235. 二叉搜索树的最近公共祖先 ● 701.二叉搜索树中的插入操作 ● 450.删除二叉搜索树中的节点 ) 235. 二叉搜索树的最近公…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
