【算法与数据结构】回溯算法、贪心算法、动态规划、图论(笔记三)
文章目录
- 七、回溯算法
- 八、贪心算法
- 九、动态规划
- 9.1 背包问题
- 9.2 01背包
- 9.3 完全背包
- 9.4 多重背包
- 十、图论
- 10.1 深度优先搜索
- 10.2 广度优先搜索
- 10.3 并查集
最近博主学习了算法与数据结构的一些视频,在这个文章做一些笔记和心得,本篇文章就写了一些基础算法和数据结构的知识点,具体题目解析会放在另外一篇文章。在学习时已经有C, C++的基础。文章附上了学习的代码,仅供大家参考。如果有问题,有错误欢迎大家留言。算法与数据结构一共有三篇文章,剩余文章可以在 【CSDN文章】晚安66博客文章索引找到。
七、回溯算法
回溯算法也可以叫回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,有递归就有回溯,因此回溯函数就是递归函数。回溯法的本质是穷举,穷举所有可能,然后选出我们想要的答案。如果想要令回溯法更加高效一些,那就加一些剪枝操作。虽然说回溯法并不高效,但是一些问题不得不用回溯法,能用暴力搜索解出来就不错了,在剪枝,除此之外没有更高效的解法。回溯法用来及诶觉以下的几个问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
回溯法解决的问题可以抽象为树形结构,因为回溯法解决的问题都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成树的深度。递归就要有终止条件,所以必然是一颗高度有限的树。回溯算法的伪代码:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}
八、贪心算法
贪心算法的本质是选择每一阶段的局部最优,从而达到全局最优。贪心算法经典问题有:背包问题,买卖股票的最佳时机。贪心算法没有固定的套路,说白了就是常识性推导加上举反例。贪心算法一般分为以下四个步骤:
- 1、将问题分解为若干个子问题
- 2、找出合适的贪心策略
- 3、求解每一个子问题的最优解
- 4、将局部最优解堆叠成全局最优解
九、动态规划
动态规划(Dynamic Programming, DP),如果一个问题有很多重叠的子问题,使用动态规划是最有效的。所有动态规划总每一个状态由上一个状态推导出来,这一点就区别于贪心算法,贪心算法没有状态变量的推导,而是从局部直接选最优的。动态规划问题可以分为下面五个步骤:
- 1、确定dp数组(dp table)以及下标的含义
- 2、确定递推公式
- 3、dp数组如何初始化
- 4、确定遍历顺序
- 5、举例推导dp数组
在很多动态规划题目当中,确定了递推公式,题目就自然的解出来了。同时,在debug动态规划题目是,将dp数组打印出来,观察其变化是否按照自己所预想的那样。
9.1 背包问题
对于背包问题来说,主要可以分为两个部分:背包和物品。背包的最大容量为 V V V,物品具有价值 W W W,体积 v v v以及每个物品的数量。如果根据物品数量进行分类,可以分为01背包问题,完全背包问题,多重背包问题和分组背包问题:
- 01背包:每种物品的数量只有一个;
- 完全背包:物品数量有无数个;
- 多重背包:不同物品的数量可以不同;
- 分组背包:按组打包,每组最多选一个。
对于找工作面试来说,掌握01背包,完全背包和多重背包就够了。LeetCode的题库中没有纯01背包问题,需要转化成01背包问题。
9.2 01背包
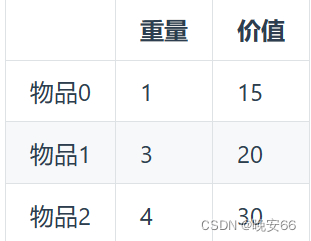
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。题目假设如下,背包最大重量为4。
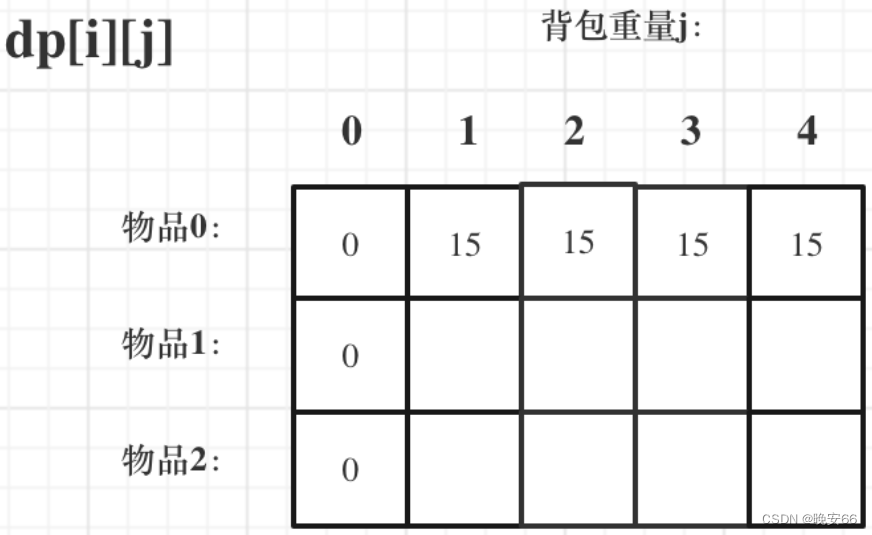
根据动态规划的五个步骤,我们首先确认dp数组的含义。假设一个二维 d p [ i ] [ j ] dp[i][j] dp[i][j]数组代表了从下标为 [ 0 − i ] [0-i] [0−i]的物品里任意取,放进容量为 j j j的背包,最大价值总和。第二步确认递归公式。不放物品:当第 i i i个物品不放进去时,此时的价值和前面的相同,有 d p [ i ] [ j ] = d p [ i − 1 ] [ j ] dp[i][j] = dp[i - 1][j] dp[i][j]=dp[i−1][j]。放物品:放物品的前提是放入的物品重量不大于背包现有容量,当然这个可以用 i f if if语句控制。假设能放进去,那么放进去之后的价值 d p [ i ] [ j ] dp[i][j] dp[i][j],可以表示为 d p [ i − 1 ] [ j − w e i g h t [ i ] ] + v a l u e [ i ] dp[i - 1][j - weight[i]] + value[i] dp[i−1][j−weight[i]]+value[i]。其中, d p [ i − 1 ] [ j − w e i g h t [ i ] ] dp[i - 1][j-weight[i]] dp[i−1][j−weight[i]]为背包容量为 j − w e i g h t [ i ] j - weight[i] j−weight[i]的时候不放物品i的最大价值, v a l u e [ i ] value[i] value[i]为物品 i i i的价值。综合以上分析,我们可以得到递归公式: d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − w e i g h t [ i ] ] + v a l u e [ i ] ) dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]) dp[i][j]=max(dp[i−1][j],dp[i−1][j−weight[i]]+value[i])。
第三步我们进行初始化,因为 i i i是由 i − 1 i-1 i−1初始化而来的,那么我们将 d p [ i ] [ 0 ] dp[i][0] dp[i][0]初始化为0。实际上我们在构建dp数组的时候可以将二维数组中的所有元素初始化为0,而非零的值将在循环遍历中被覆盖。然后初始化第一行当 j > w e i g h t [ i ] j>weight[i] j>weight[i]时(背包可以放假物品0), d p [ 0 ] [ j ] dp[0][j] dp[0][j]应该是 v a l u e [ 0 ] value[0] value[0]。第四步,确定遍历顺序。遍历的两个维度分别是物品和背包重量,遍历物品相对比遍历背包重量更容易理解:
// 初始化 dp
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品for(int j = 0; j <= bagweight; j++) { // 遍历背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}
}
当然,上述的dp数组也可以写成一维滚动数组形式。下面的代码舍去了初始化的代码,舍去下标二维dp数组的下标 i i i从而变成了一维数组。主要原因是 d p [ i − 1 ] [ j ] dp[i - 1][j] dp[i−1][j]完全可以用 d p [ j ] dp[j] dp[j]来表示。二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。倒序遍历是为了保证物品i只被放入一次!。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
举一个例子:物品0的重量weight[0] = 1,价值value[0] = 15。如果正序遍历dp[1] = dp[1 - weight[0]] + value[0] = 15,dp[2] = dp[2 - weight[0]] + value[0] = 30。此时dp[2]就已经是30了,意味着物品0,被放入了两次,所以不能正序遍历。
倒序就是先算dp[2]。dp[2] = dp[2 - weight[0]] + value[0] = 15 (dp数组已经都初始化为0),dp[1] = dp[1 - weight[0]] + value[0] = 15。所以从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
class Solution { // 一维dp数组(滚动数组形式)
public:int bag01(const vector<int> weight, const vector<int> value, const int bagweight) {vector<int> dp(vector<int>(bagweight + 1, 0));for (int i = 0; i < weight.size(); i++) { // 遍历物品for (int j = bagweight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}return dp[bagweight];}
};
简言之,一维dp数组和二维dp数组的区别在于一维的空间复杂度低,二维的更容易理解(初学者用二维即可)。以上的完整代码如下:
# include <iostream>
# include <vector>
using namespace std;class Solution {
public:int bag01(const vector<int> weight, const vector<int> value, const int bagweight) {vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));for (int j = weight[0]; j <= bagweight; j++) { // 初始化dp[0][j] = value[0];}for (int i = 1; i < weight.size(); i++) { // 遍历物品for (int j = 0; j <= bagweight; j++) { // 遍历背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}return dp[weight.size() - 1][bagweight];}
};int main() {Solution s1;vector<int> weight = { 1, 3, 4 };vector<int> value = { 15, 20, 30 };int bagweight = 4;int result = s1.bag01(weight, value, bagweight);cout << result << endl;system("pause");return 0;
}
9.3 完全背包
完全背包问题可以描述为:有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。依然假设背包最大重量为4。

为了保证每个物品仅被添加一次,01背包内嵌的循环是从大到小遍历。而完全背包的物品是可以添加多次的,所以要从小到大去遍历。
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
9.4 多重背包
有N种物品和一个容量为V的背包。第 i i i种物品最多有 M i M_i Mi件可用,每件耗费的空间是 C i C_i Ci ,价值是 W i W_i Wi。求解将哪些物品装入背包可使这些物品的耗费的空间,总和不超过背包容量,且价值总和最大。
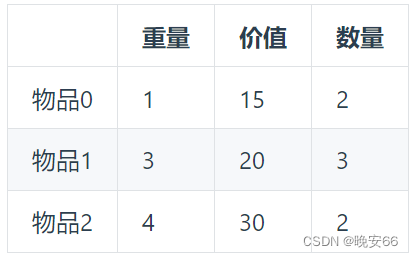
我们将物品数量摊开,其实可以将多重背包问题转换成01背包。例如:背包最大重量为10。物品的重量、价值和数量如下。那么可以转化成7个物品,每个物品只能用一次。这样就是一个01背包问题。因此我们在01背包的基础之上加上遍历个数即可。
#include<iostream>
#include<vector>
using namespace std;class Solution {
public:int Multip_Bag(int bagWeight, int nItem, vector<int> weight, vector<int> value, vector<int> nums) {vector<int> dp(bagWeight + 1, 0);for (int i = 0; i < nItem; i++) { // 遍历物品for (int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量// 以上为01背包,然后加一个遍历个数for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);}}}return dp[bagWeight];}
};int main() {int bagWeight = 10, nItem = 3;vector<int> weight = {1, 3, 4}, value = {15, 20, 30}, nums = {2, 3, 2};Solution s1;int result = s1.Multip_Bag(bagWeight, nItem, weight, value, nums);cout << result << endl;system("pause");return 0;
}
十、图论
10.1 深度优先搜索
DFS和BFS的区别:
- 深度优先搜索(Depth First Search, DFS)是沿着一个方向搜索,不到黄河不死心,直到遇到绝境了,搜不下去了,再换方向(回溯)。
- 广度优先搜索(Breadth First Search, BFS)是先把本节点所连接的所有节点遍历一遍,走到下一个节点的时候,再把连接节点的所有节点遍历一遍,搜索的方向是四面八方的,因此被称为广度优先搜索。
因为DFS搜索就一个方向,并且需要回溯,所以用递归来实现是最方便的。二叉树遍历的递归法是DFS,而二叉树遍历的迭代法是BFS。
void dfs(参数) {处理节点dfs(图,选择的节点); // 递归回溯,撤销处理结果
}
回溯算法本质上也是一种DFS过程,DFS搜索过程可以笼统的划分为三步。一是确定输入参数;二是确定终止条件;三是处理目前搜索节点的出发路径。
void dfs(输入参数) {if (终止条件) {存放结果;return;}for (选择:本节点所连接的其他节点) {处理节点;dfs(图,选择的节点); // 递归回溯,撤销处理结果}
}
10.2 广度优先搜索
如果说深搜是一条路跑到黑然后再回溯的搜索方式,那么广搜就是一圈一圈的搜索过程。广搜的搜索方式就适合解决两个点之间最短路径的问题。因为广搜是从起点出发,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路。
10.3 并查集
并查集是当我们需要判断两个元素是否在同一个集合里的时候,我们就要想到用并查集。并查集常用来解决连通性问题。并查集有以下两个功能:
- 将两个元素添加到一个集合中。
- 判断两个元素在不在同一个集合。
设想我们将三个元素A, B,C(都是int类型)放在同一集合,其实就是将三个元素连通在一起。只需要一个一维数组来表示:father[A] = B, father[B] = C,father[C] = C。当我们使用find函数去寻找数组的元素,如果数组元素的根相同,这样就表示A与B与C连通。
// 将v,u 这条边加入并查集
void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return; // 如果发现根相同,则说明在一个集合,不同两个节点相连直接返回father[v] = u;
}
find函数通过数组下标找到数组元素,一层一层寻根过程,代码如下:
// 并查集里寻根的过程
int find(int u) {if (u == father[u]) return u; // 如果根就是自己,直接返回else return find(father[u]); // 如果根不是自己,就根据数组下标一层一层向下找
}
find函数寻根的过程是通过递归的方式,不断获取father数组下标对应的数值,最终找到集合的根。而这很像在一个多叉树中,从叶子节点出发,找到根节点的过程。如果说这颗树的高度很深,每次寻根需要递归很多次。
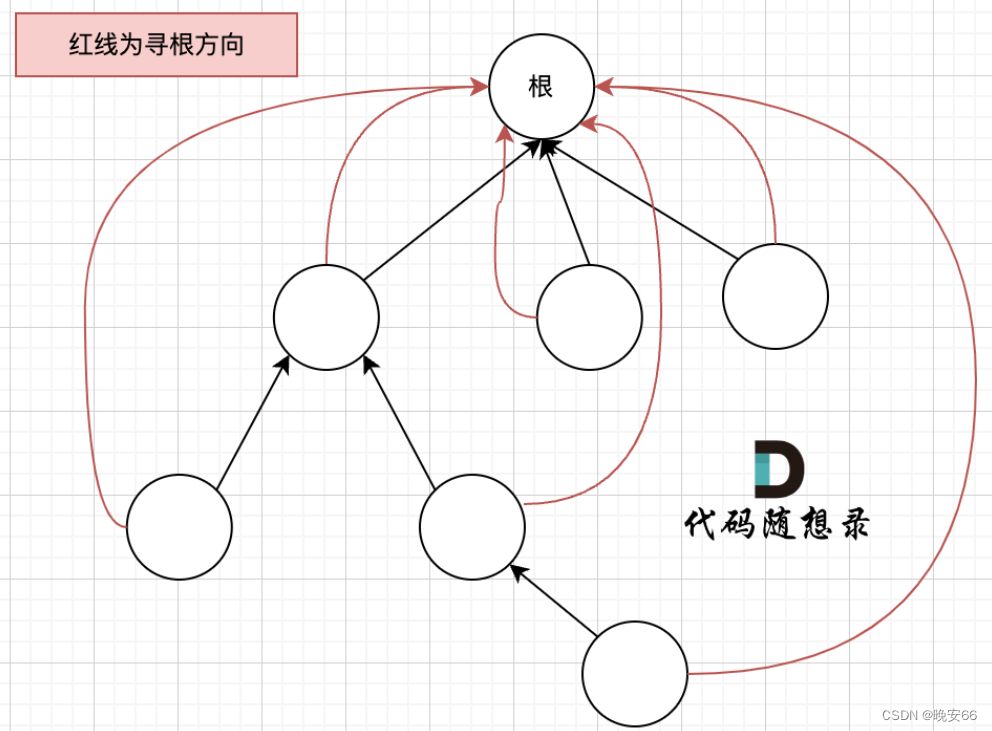
而我们的目的是需要知道这些节点在同一个根下就可以,因此让多茶树的叶子节点直接指向根即可,每次寻根只需要一次。
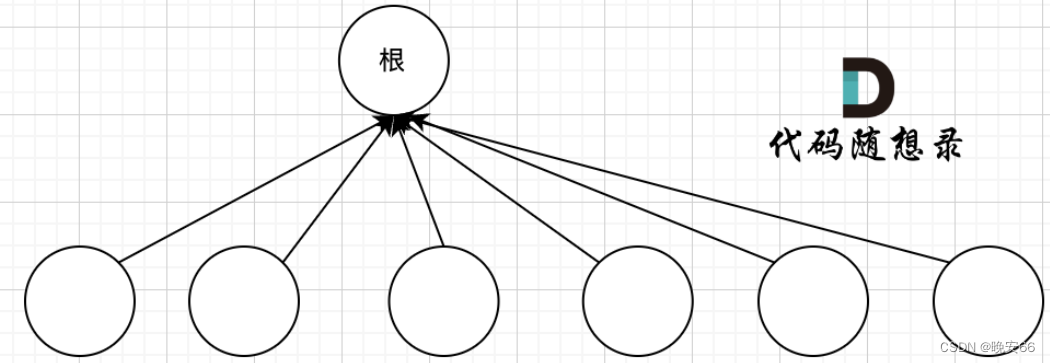
要实现这样的路径压缩过程,只需要在递归过程中,让father[u]接住 递归函数 find(father[u])的返回结果。这样是让u的父节点直接变成find函数返回的根节点。进一步可以用三元表达式精简代码。
// 并查集里寻根的过程
int find(int u) {if (u == father[u]) return u;else return father[u] = find(father[u]); // 路径压缩
}
int find(int u) {return u == father[u] ? u : father[u] = find(father[u]);
}
同时,father数组初始化的时候要令 father[i] = i,默认指向自己。
// 并查集初始化
void init() {for (int i = 0; i < n; ++i) {father[i] = i;}
}
如果通过find函数找到两个元素属于同一个根的话,那么这两个元素就是同一个集合,代码如下:
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;
}
结合以上加入并查集join、寻根find、初始化init和判断是否同一集合isSame函数,我们就得到一个并查集完整模板:
int n = 1005; // n根据题目中节点数量而定,一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构// 并查集初始化
void init() {for (int i = 0; i < n; ++i) {father[i] = i;}
}
// 并查集里寻根的过程
int find(int u) {return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;
}// 将v->u 这条边加入并查集
void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return ; // 如果发现根相同,则说明在一个集合,不同两个节点已经相连,直接返回father[v] = u;
}
总结下来,并查集主要具有三个功能:
- 1、寻找根节点函数find(int u),也就是判断这个节点的祖先节点是哪个;
- 2、将两个节点接入到同一集合,join(int u, int v)函数,可以将两个节点连接在同一根节点上;
- 3、判断两个节点是否在同一集合中,使用isSame(int u, int v)函数,就是判断两个节点是不是同一个根节点。
复杂度分析:
- 时间复杂度: O ( 1 ) O(1) O(1),真实的复杂度在 O ( l o g n ) O(logn) O(logn)和 O ( 1 ) O(1) O(1)之间,且随着查询或者合并操作的增加,时间复杂度越来越趋近于 O ( 1 ) O(1) O(1)。
- 空间复杂度: O ( n ) O(n) O(n), 申请一个father数组。
相关文章:

【算法与数据结构】回溯算法、贪心算法、动态规划、图论(笔记三)
文章目录 七、回溯算法八、贪心算法九、动态规划9.1 背包问题9.2 01背包9.3 完全背包9.4 多重背包 十、图论10.1 深度优先搜索10.2 广度优先搜索10.3 并查集 最近博主学习了算法与数据结构的一些视频,在这个文章做一些笔记和心得,本篇文章就写了一些基础…...

【pytorch】常用代码
文章目录 条件与概率torch.tensor()torch.rand()torch.randn()torch.randint()torch.multinominal() 逻辑运算torch.argmax()torch.max()torch.sum()torch.tanh()torch.pow() 功能性操作 torch.nn.functionalF.normalize()F.elu()F.relu()F.softmax() 张量计算torch.zeros()tor…...
GB28181 —— Ubuntu20.04下使用ZLMediaKit+WVP搭建GB28181流媒体监控平台(连接带云台摄像机)
最终效果 简介 GB28181协议是视频监控领域的国家标准。该标准规定了公共安全视频监控联网系统的互联结构, 传输、交换、控制的基本要求和安全性要求, 以及控制、传输流程和协议接口等技术要求,是视频监控领域的国家标准。GB28181协议信令层面使用的是SIP(Session Initiatio…...
图片录入设备、方式与质量对图片转Excel的影响
随着数字化时代的到来,图片已经成为人们日常生活中不可或缺的一部分。在各行各业中,图片的应用越发广泛,从而促使了图片处理技术的快速发展。然而,图片的质量对于后续数据处理和分析的准确性和可靠性有着至关重要的影响。本文将从…...

Linux:ACL权限,特殊位和隐藏属性
目录 一.什么是ACL 二.操作步骤 ① 添加测试目录、用户、组,并将用户添加到组 ② 修改目录的所有者和所属组 ③ 设定权限 ④ 为临时用户分配权限 ⑤ 验证acl权限 ⑥ 控制组的acl权限 三. 删除ACL权限 一.什么是ACL 访问控制列表 (Access Control List):ACL 通…...
FL Studio21中文版本价格多少?值不值得购买?
FL Studio,也被称为Fruity Loops,是一款非常受欢迎的数字音频工作站(DAW),适合广泛的音乐制作人群使用。以下是适合使用FL Studio的人群: 初学者:FL Studio拥有直观且用户友好的界面,…...

【论文阅读】ICCV 2023 计算和数据高效后门攻击
文章目录 一.论文信息二.论文内容1.摘要2.引言3.主要图表4.结论 一.论文信息 论文题目: Computation and Data Efficient Backdoor Attacks(计算和数据高效后门攻击) 论文来源: 2023-ICCV(CCF-A) 论文团…...
JavaAPI常用类03
目录 java.lang.Math Math类 代码 运行 Random类 代码 运行 Date类/Calendar类/ SimpleDateFormat类 Date类 代码 运行 Calendar类 代码 运行 SimpleDateFormat类 代码一 运行 常用的转换符 代码二 运行 java.math BigInteger 代码 运行 BigDecimal …...
SpringBoot/Java中OCR实现,集成Tess4J实现图片文字识别
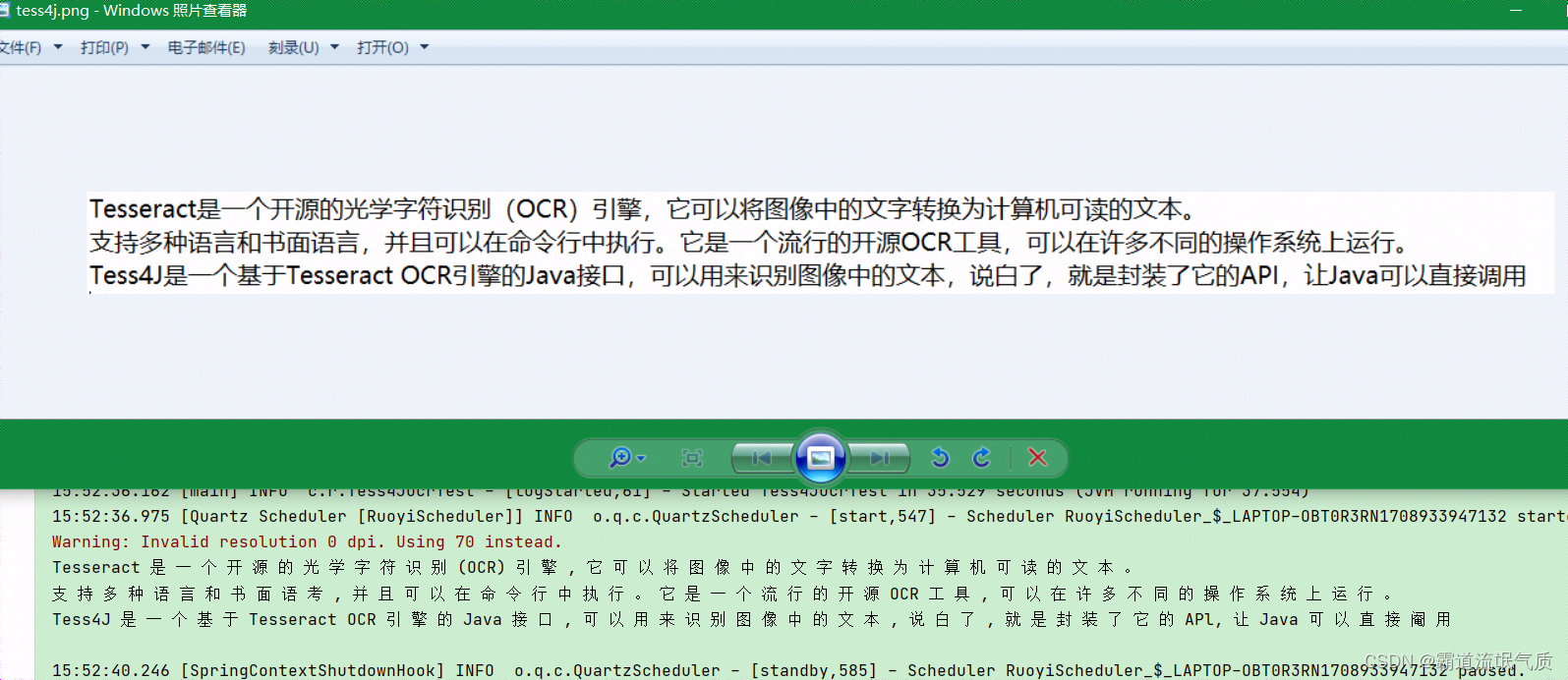
场景 Tesseract Tesseract是一个开源的光学字符识别(OCR)引擎,它可以将图像中的文字转换为计算机可读的文本。 支持多种语言和书面语言,并且可以在命令行中执行。它是一个流行的开源OCR工具,可以在许多不同的操作系…...
【深度学习目标检测】十九、基于深度学习的芒果计数分割系统-含数据集、GUI和源码(python,yolov8)
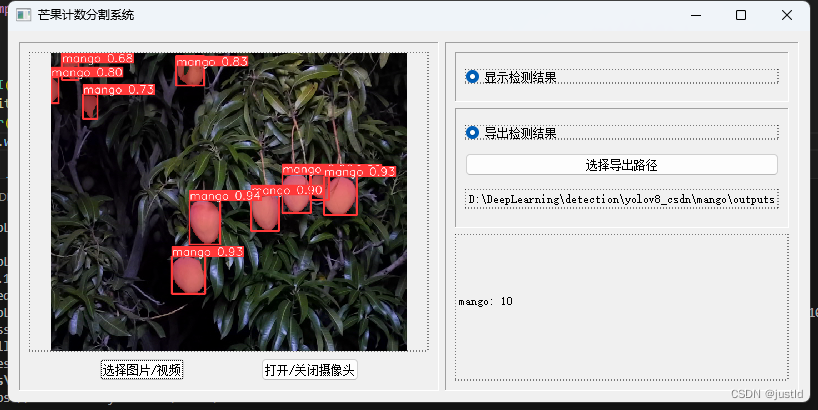
使用深度学习算法检测芒果具有显著的优势和应用价值。以下是几个主要原因: 特征学习的能力:深度学习,特别是卷积神经网络(CNN),能够从大量的芒果图像中自动学习和提取特征。这些特征可能是传统方法难以手动…...
-多人联机模式开发环境搭建)
骑砍战团MOD开发(48)-多人联机模式开发环境搭建
一.多人联机模式网络拓扑图 <1.局域网网络拓扑图 <2.互联网网络拓扑图 二.多人联机模式配置 MOD目录下module.ini修改配置项 has_multiplayer 1 has_single_player 1 三.服务端创建 引擎内置presentation页面: prsnt_game_multiplayer_admin_panel start_multi…...

Java+SpringBoot+Vue+MySQL:美食推荐系统的技术革新
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...
【服务发现--ingress】
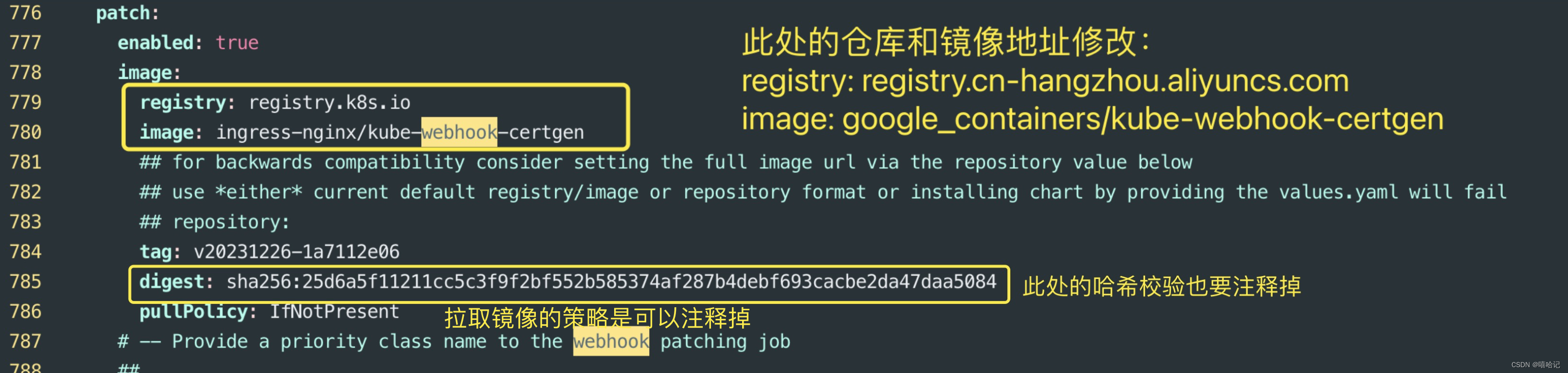
1、ingress介绍 Ingress 提供从集群外部到集群内服务的 HTTP 和 HTTPS 路由。 流量路由由 Ingress 资源所定义的规则来控制。 Ingress 是对集群中服务的外部访问进行管理的 API 对象,典型的访问方式是 HTTP。 Ingress 可以提供负载均衡、SSL 终结和基于名称的虚拟…...
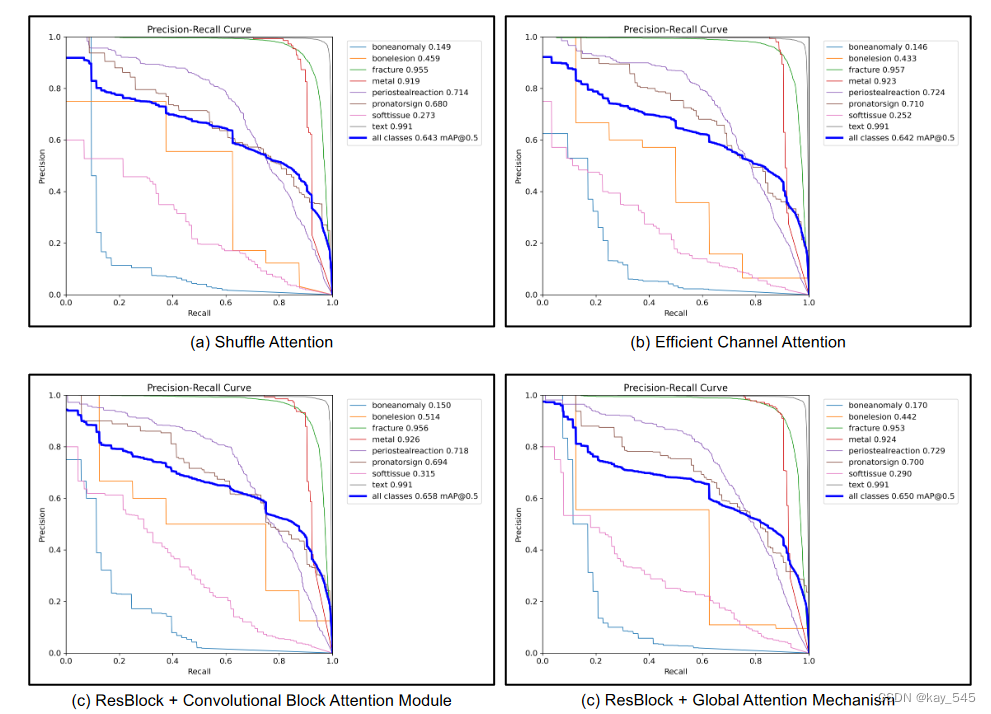
Yolov8有效涨点:YOLOv8-AM,添加多种注意力模块提高检测精度,含代码,超详细
前言 2023 年,Ultralytics 推出了最新版本的 YOLO 模型。注意力机制是提高模型性能最热门的方法之一。 本次介绍的是YOLOv8-AM,它将注意力机制融入到原始的YOLOv8架构中。具体来说,我们分别采用四个注意力模块:卷积块注意力模块…...

苹果分拣检测YOLOV8NANO
苹果分拣,可以检测成熟、切片、损坏、不成熟四种类型,YOLOV8NANO,训练得到PT模型,然后转换成ONNX,OPENCV的DNN调用,支持C,PYTHON 苹果分拣检测YOLOV8NANO,检测四种类型苹果...

使用 Verilog 做一个可编程数字延迟定时器 LS7211-7212
今天的项目是在 Verilog HDL 中实现可编程数字延迟定时器。完整呈现了延迟定时器的 Verilog 代码。 所实现的数字延迟定时器是 CMOS IC LS7212,用于生成可编程延迟。延迟定时器的规格可以在这里轻松找到。基本上,延迟定时器有 4 种操作模式:…...

戏说c语言文章汇总
c语言的起源GNU C和标准C第一篇: hello c!第二篇: 为什么需要编译第三篇: 当你运行./a.out时,发生了什么?第四篇: 简单的加法器第五篇: 两个正数相加竟然变成了负数!第六篇: 西西弗斯推石头(循环)第七篇: 九九乘法表(双循环)第八篇: 如果上天…...
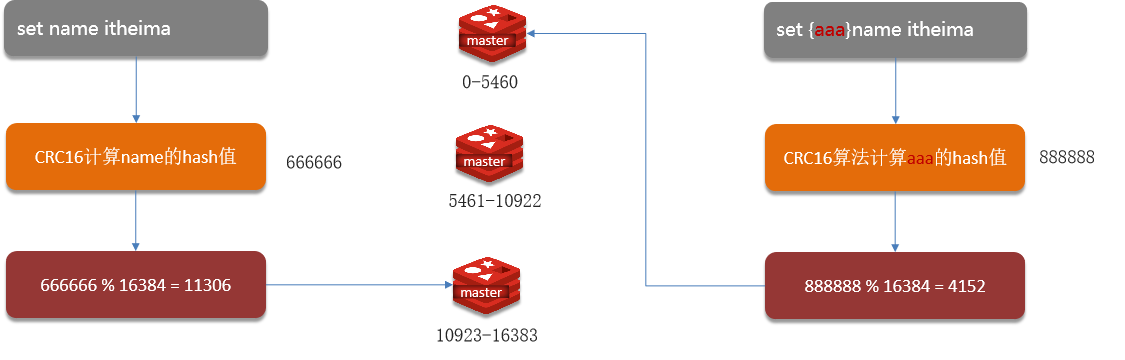
面试redis篇-12Redis集群方案-分片集群
原理 主从和哨兵可以解决高可用、高并发读的问题。但是依然有两个问题没有解决: 海量数据存储问题高并发写的问题 使用分片集群可以解决上述问题,分片集群特征: 集群中有多个master,每个master保存不同数据每个master都可以有…...
【Java EE初阶二十三】servlet的简单理解
1. 初识servlet Servlet 是一个比较古老的编写网站的方式,早起Java 编写网站,主要使用 Servlet 的方式,后来 Java 中产生了一个Spring(一套框架),Spring 又是针对 Servlet 进行了进一步封装,从而让我们编写网站变的更简单了;Sprin…...

c++ http操作接口
很简单的使用libcurl来操作http与服务器来通讯,包含http与https,对外只开放 #include "request.h" #include "response.h" #include "url.h" 三个头文件,简单易用,使用的实例如下: vo…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
