多重背包问题中的二进制状态压缩
1.多重背包问题

经典的多重背包问题和01背包问题的相似之处在于二者的一维遍历顺序都是从右侧往左侧遍历。
同时多重背包的一维写法不比二维写法降低时间复杂度。
2.多重背包标准写法:(平铺展开形式)
class Solution {public int maxValue(int N, int C, int[] s, int[] v, int[] w) {int[] dp = new int[C + 1];for (int i = 0; i < N; i++) {for (int j = C; j >= v[i]; j--) {for (int k = 0; k <= s[i] && j >= k * v[i]; k++) {dp[j] = Math.max(dp[j], dp[j - k * v[i]] + k * w[i]);}}}return dp[C];}
}因为转换为一维之后,无法记录每个物品的使用次数,所以多重背包的一维写法并不能减低时间复杂度,注意完全版背包的一维写法是能够降低时间复杂度的。此处的代码与01背包十分相似。01背包的代码如下:
class Solution {public int maxValue(int N, int C, int[] v, int[] w) {int[] dp = new int[C + 1];for (int i = 0; i < N; i++) {for (int j = C; j >= v[i]; j--) {// 不选该物品int n = dp[j]; // 选择该物品int y = dp[j-v[i]] + w[i]; dp[j] = Math.max(n, y);}}return dp[C];}
}3.二进制压缩形式的多重背包
上述的多重背包的解法实际上是将带选择的m个物品平着展开为[1,1,1....](共计m个),具体可以查看最后一个for循环的写法,不断尝试一个一个的将数据加进去。
实际上这种解法只能解决数据量为平方级别的数据。而二进制解法则是将原本为 n 的物品用 ceil(log(n)) 个数来代替,从而降低算法复杂度。
学过 Linux 的都知道文件权限最高是 7,代表拥有读、写、执行的权限,但其实这个 7 是对应了 1、2、4 三个数字的,也就是 r:1、w:2、x:4 ,三种权限的组合共有 8 种可能性
7 可以用 1、2、4 来代替,像刚刚提到的 10 ,我们可以使用 1、2、4、3 来代替,你可能会有疑问,为什么是 1、2、4、3,而不是 1、2、4、6 或者 1、2、4、8 呢?
其实把他们几个数加起来就知道了,1、2、4、6 可以表达的范围是 0~13,而 1、2、4、8 可以表达的范围是 0~15,而我们要求的是表达 10,大于 10 的范围是不能被选择的。
所以我们可以在 1、2、4 (表达的范围是 0~7)的基础上,增加一个数 3(由 10 - 7 而来),这样就能满足我们需要表达的范围 0~10。
具体的转换为二进制的代码如下所示:
class Solution {public int maxValue(int N, int C, int[] s, int[] v, int[] w) {// 扁平化List<Integer> worth = new ArrayList<>();List<Integer> volume = new ArrayList<>();// 我们希望每件物品都进行扁平化,所以首先遍历所有的物品for (int i = 0; i < N; i++) {// 获取每件物品的出现次数int val = s[i];// 进行扁平化:如果一件物品规定的使用次数为 7 次,我们将其扁平化为三件物品:1*重量&1*价值、2*重量&2*价值、4*重量&4*价值// 三件物品都不选对应了我们使用该物品 0 次的情况、只选择第一件扁平物品对应使用该物品 1 次的情况、只选择第二件扁平物品对应使用该物品 2 次的情况,只选择第一件和第二件扁平物品对应了使用该物品 3 次的情况 ... //注意此处是等号,可能正好减完for (int k = 1; k <= val; k *= 2) { val -= k;worth.add(w[i] * k);volume.add(v[i] * k);}if (val > 0) {//没有正好减完worth.add(w[i] * val);volume.add(v[i] * val);}}// 0-1 背包问题解决方案int[] dp = new int[C + 1];for (int i = 0; i < worth.size(); i++) {for (int j = C; j >= volume.get(i); j--) {dp[j] = Math.max(dp[j], dp[j - volume.get(i)] + worth.get(i));}}return dp[C];}
}相关文章:

多重背包问题中的二进制状态压缩
1.多重背包问题 经典的多重背包问题和01背包问题的相似之处在于二者的一维遍历顺序都是从右侧往左侧遍历。 同时多重背包的一维写法不比二维写法降低时间复杂度。 2.多重背包标准写法:(平铺展开形式) class Solution {public int maxValue(int N, int C, int[] s…...

汇编语言程序设计(四)之汇编指令
系列文章 汇编语言程序设计(一) 汇编语言程序设计(二)之寄存器 汇编语言程序设计(三)之汇编程序 汇编指令 1. 数据传输指令 指令包括:MOV、XCHG、XLAT、LEA、LDS、LES、PUSH、POP、PUSHF、LA…...

Vant2 源码分析之 vant-sticky
前言 原打算借鉴 vant-sticky 源码,实现业务需求的某个功能,第一眼看以为看懂了,拿来用的时候,才发现一知半解。看第二遍时,对不起,是我肤浅了。这里侧重分析实现原理,其他部分不拓展开来&…...
【自然语言处理】【大模型】大语言模型BLOOM推理工具测试
相关博客 【自然语言处理】【大模型】大语言模型BLOOM推理工具测试 【自然语言处理】【大模型】GLM-130B:一个开源双语预训练语言模型 【自然语言处理】【大模型】用于大型Transformer的8-bit矩阵乘法介绍 【自然语言处理】【大模型】BLOOM:一个176B参数…...
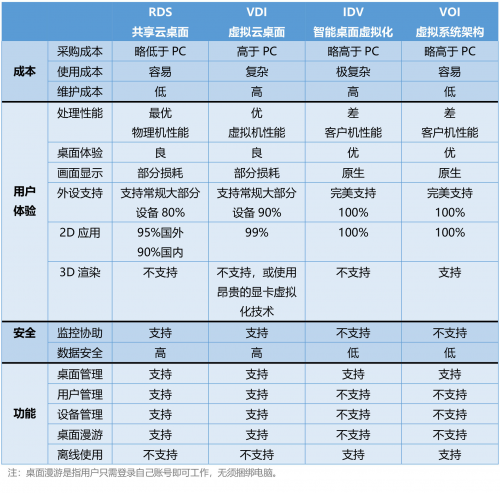
云桌面技术初识:VDI,IDV,VOI,RDS
VDI(Virtual Desktop Infrastucture,虚拟桌面架构),俗称虚拟云桌面 VDI构架采用的“集中存储、集中运算”构架,所有的桌面以虚拟机的方式运行在服务器硬件虚拟化层上,桌面以图像传输的方式发送到客户端。 …...

基于本地centos构建gdal2.4.4镜像
1.前言 基于基础镜像构建gdal环境一般特别大,一般少则1.6G,多则2G甚至更大,这对于镜像的迁移造成了极大的不便。究其原因在于容器中有大量的源码文件以及编译中间过程文件,还要大量编译需要的yum库。本文主要通过在centos系统上先…...

生产环境线程问题排查
线程状态的解读RUNNABLE线程处于运行状态,不一定消耗CPU。例如,线程从网络读取数据,大多数时间是挂起的,只有数据到达时才会重新唤起进入执行状态。只有Java代码显式调用sleep或wait方法时,虚拟机才可以精准获取到线程…...

Day908.joinsnljdist和group问题和备库自增主键问题 -MySQL实战
join&snlj&dist和group问题和备库自增主键问题 Hi,我是阿昌,今天学习记录的是关于join&snlj&dist和group问题和备库自增主键问题的内容。 一、join 的写法 join 语句怎么优化?中,在介绍 join 执行顺序的时候&am…...

算法 - 剑指Offer 丑数
题目 我们把只包含质因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。 解题思路 这题我使用最简单方法去做, 首先我们可以获取所有2n,3n,5*n的丑数,只是我们这里暂时无法排序,并且可能…...
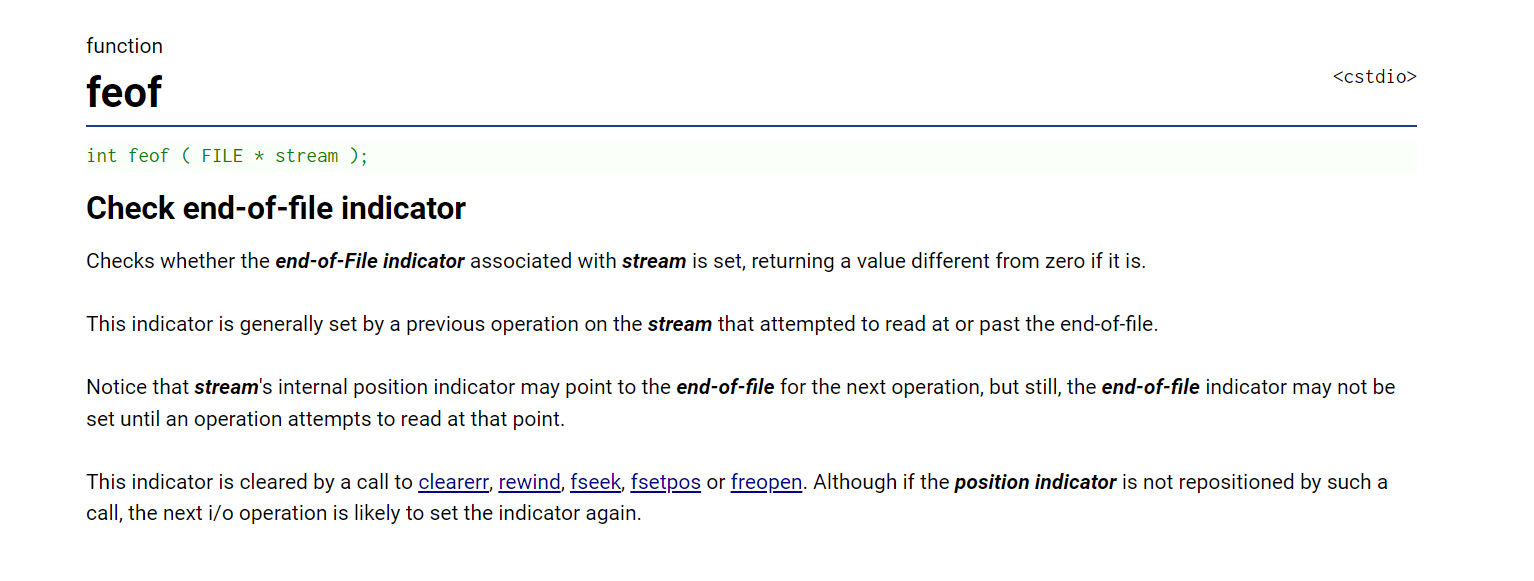
【ONE·C || 文件操作】
总言 C语言:文件操作。 文章目录总言1、文件是什么?为什么需要文件?1.1、为什么需要文件?1.2、文件是什么?2、文件的打开与关闭2.1、文件指针2.2、文件打开和关闭:fopen、fclose2.3、文件使用方式3、文…...
cmd窗口中java命令报错。错误:找不到或无法加载主类 java的jdk安装过程中踩过的坑
错误: 找不到或无法加载主类 HelloWorld 遇到这个问题时,我尝试过网上其他人的做法。有试过添加classpath,也有试过删除classpath。但是依然报错,这里javac可以编译通过,说明代码应该是没有问题的。只是在运行是出现了错误。我安装…...
)
Breathwork(呼吸练习)
查了下呼吸练习相关内容,做个记录。我又在油管学习啦。 喜欢在you. tube看一些self-help相关的内容。比如学习方法、拉伸、跑步、力量举、自重锻炼等等。 总是听Obi Vicent说起Breathwork,比如: My 6am Morning Routine | New Healthy Habit…...
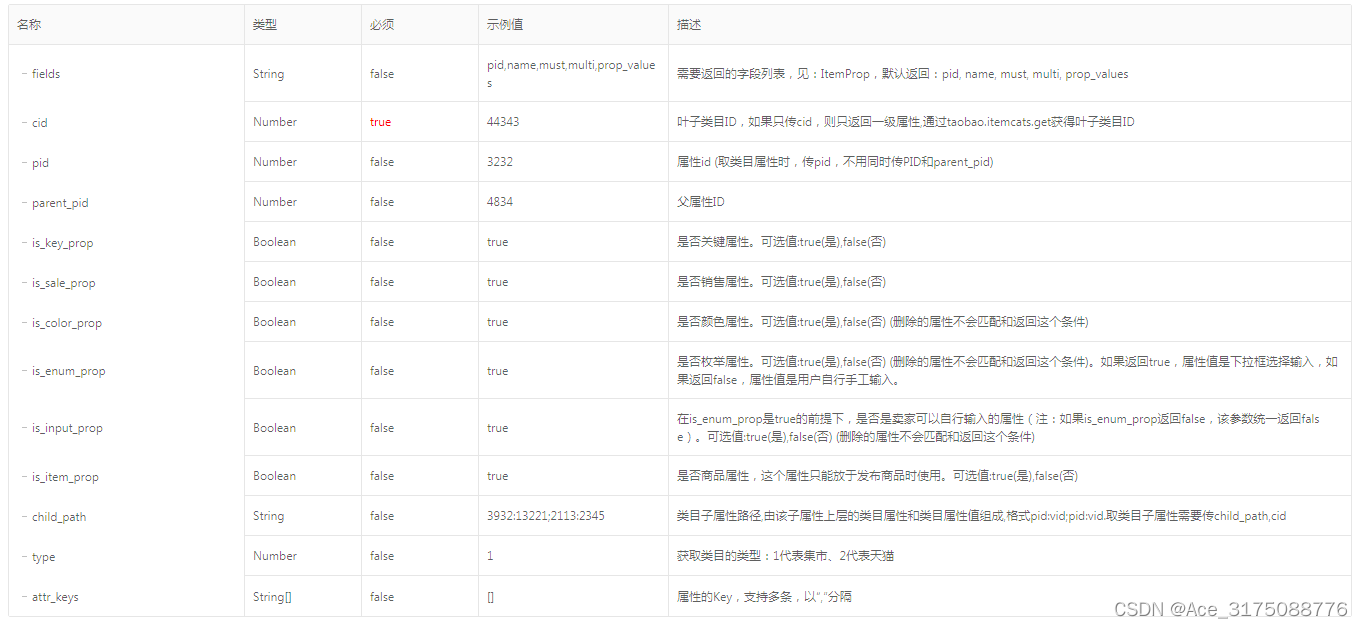
taobao.itemprops.get( 获取标准商品类目属性 )
¥开放平台基础API不需用户授权 通过设置必要的参数,来获取商品后台标准类目属性,以及这些属性里面详细的属性值prop_values。 公共参数 请求地址: HTTP地址 http://gw.api.taobao.com/router/rest 公共请求参数: 公共响应参数: 请求参数 点…...
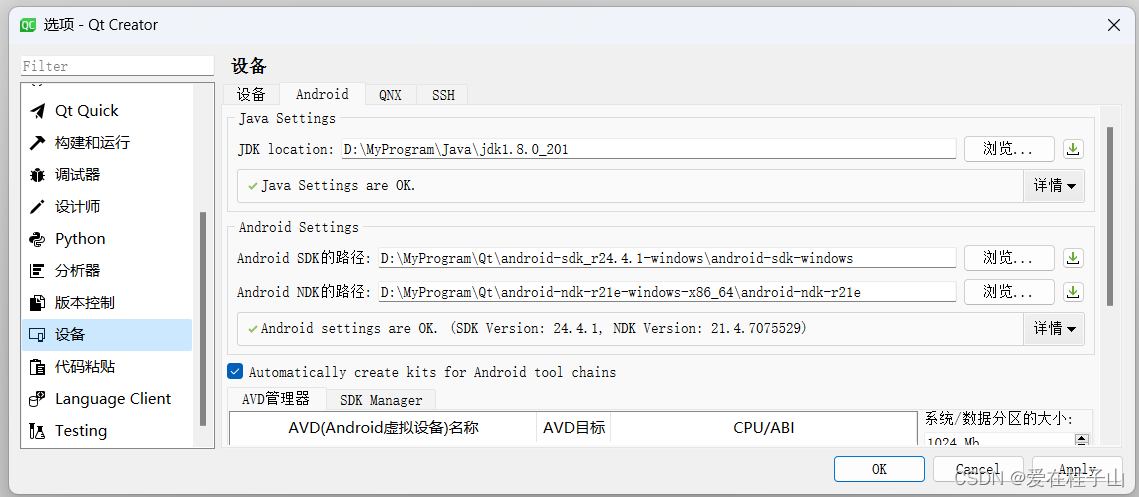
QT配置安卓环境(保姆级教程)
目录 下载环境资源 JDK1.8 NDK SDK 安装QT 配置环境 下载环境资源 JDK1.8 介绍JDK是Java开发的核心工具,为Java开发者提供了一套完整的开发环境,包括开发工具、类库和API等,使得开发者可以高效地编写、测试和运行Java应用程序。 下载…...
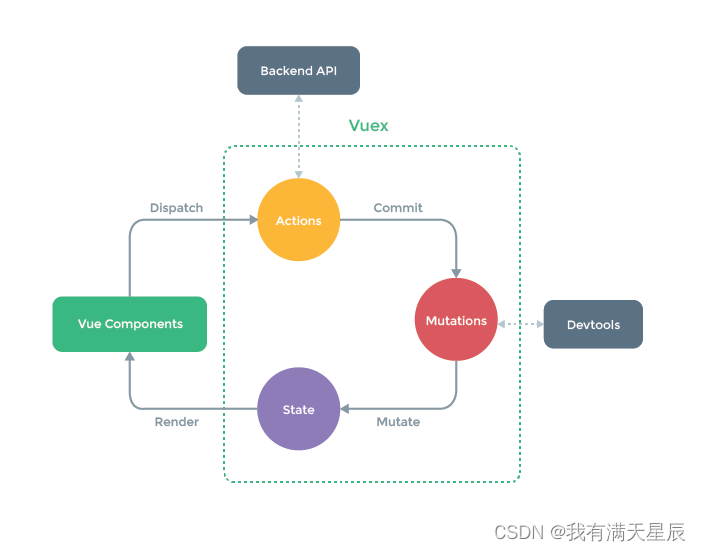
【uni-app教程】八、UniAPP Vuex 状态管理
八、UniAPP Vuex 状态管理 概念 Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式。它采用集中式存储管理应用的所有组件的状态,并以相应的规则保证状态以一种可预测的方式发生变化。 应用场景 Vue多个组件之间需要共享数据或状态。 关键规则 State:…...
)
同花顺测试面经(30min)
大概三十分钟,面试官人还挺好的 1.自我介绍 2.详细问你了自我介绍中的一个实习经历 3.对我们公司有什么了解 !!(高频) 4.对测试有什么看法,为什么选测试 5.黑盒白盒分别是什么 6.对测试左移有什么看法…...

C++-简述#ifdef、#else、#endif和#ifndef的作用
回答如下: #ifdef,#else,#endif和#ifndef都是预处理指令,用于条件编译。#ifdef:这个指令用来判断一个宏是否已经被定义过,如果已经定义过,则执行后面的代码块。#else:这个指令一般与…...

VictoriaMetrics 集群部署
官网 ## 官网 https://github.com/VictoriaMetrics/VictoriaMetrics 集群角色详解 VictoriaMetrics 集群模式。主要由 vmstorage ,vminsert,vmselect 三部分组成,这三个组件每个组件都可以单独进行扩展。其中: vmstorage 负责提供数据存储服务vminsert 是数据存…...
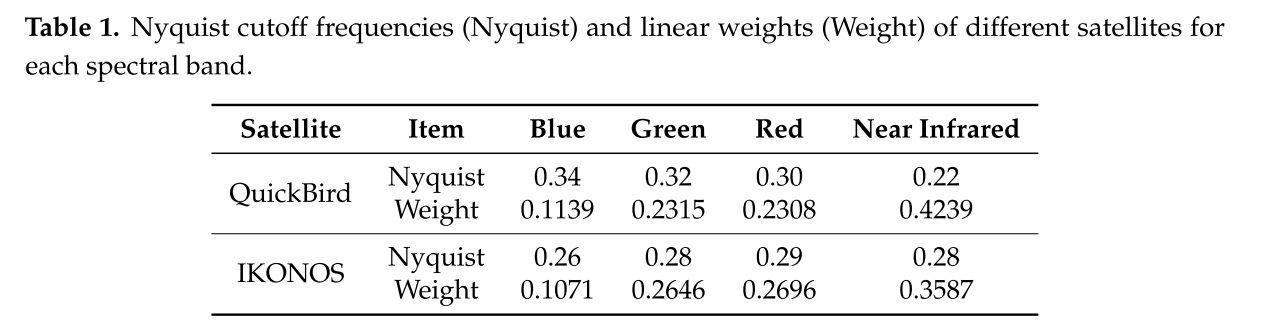
【基于感知损失的无监督泛锐化】
PercepPan: Towards Unsupervised Pan-Sharpening Based on Perceptual Loss (PercepPan:基于感知损失的无监督泛锐化) 在基于神经网络的全色锐化文献中,作为地面实况标签的高分辨率多光谱图像通常是不可用的。为了解决这个问题…...

在vercel上用streamlit部署网站
Verce和Streamlit都是非常流行的Web应用程序部署平台。以下是从零开始在Vercel上部署Streamlit应用程序的一些基本步骤。 安装 Streamlit 在本地计算机上安装Streamlit。可以轻松地通过在命令行中运行以下命令来安装: pip install streamlit为 Streamlit 应用程序…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
