xmu 离散数学 卢杨班作业详解【4-7章】
文章目录
- 第四章 二元关系和函数
- 4.
- 6.2
- 9
- 11
- 12
- 16
- 18.1
- 20.2
- 22.1
- 23
- 28
- 34
- 第五章 代数系统的一般概念
- 2判断二元运算是否封闭
- 3
- 4
- 8
- 11
- 12
- 14
- 第六章 几个典型的代数系统
- 1.
- 5.
- 6.
- 7.
- 11.
- 12
- 15
- 16
- 18
- 第七章 图的基本概念
- 1
- 2
- 4
- 7
- 9
- 11
- 12
- 15
第四章 二元关系和函数
4.
A={1,2,3}
恒等关系
IA={<1,1>,<2,2>,<3,3>}I_A=\{ <1,1>,<2,2>,<3,3>\}IA={<1,1>,<2,2>,<3,3>}
全域关系EA={<1,1>,<1,2>,<1,3>,<2,1>,<2,2>,<2,3>,<3,1>,<3,2>,<3,3>}E_A=\{<1,1>,<1,2>,<1,3>,<2,1>,<2,2>,<2,3>,<3,1>,<3,2>,<3,3>\}EA={<1,1>,<1,2>,<1,3>,<2,1>,<2,2>,<2,3>,<3,1>,<3,2>,<3,3>}
小于等于关系
LA={<1,1>,<1,2>,<1,3>,<2,2>,<2,3>,<3,3>}L_A=\{<1,1>,<1,2>,<1,3>,<2,2>,<2,3>,<3,3>\}LA={<1,1>,<1,2>,<1,3>,<2,2>,<2,3>,<3,3>}
整除关系
DA={<1,1>,<1,2>,<1,3>,<2,2>,<3,3>}D_A=\{<1,1>,<1,2>,<1,3>,<2,2>,<3,3>\}DA={<1,1>,<1,2>,<1,3>,<2,2>,<3,3>}
6.2
A={1,2,4,6},列出R
R={(x,y)|x,y∈\in∈A∧\wedge∧ |x-y|=1}
R={<1,2>,<2,1>}R=\{<1,2>,<2,1>\}R={<1,2>,<2,1>}
9
R={<0,1>,<0,2>,<0,3>,<1,2>,<1,3>,<2,3>}R=\{<0,1>,<0,2>,<0,3>,<1,2>,<1,3>,<2,3>\}R={<0,1>,<0,2>,<0,3>,<1,2>,<1,3>,<2,3>}
求R∘\circ∘R,R−1R^{-1}R−1
R∘R={<0,2>,<0,3>,<0,3>,<1,3>}R\circ R=\{<0,2>,<0,3>,<0,3>,<1,3>\}R∘R={<0,2>,<0,3>,<0,3>,<1,3>}
R−1={<1,0>,<2,0>,<3,0>,<2,1>,<3,1>,<3,2>}R^{-1}=\{<1,0>,<2,0>,<3,0>,<2,1>,<3,1>,<3,2>\}R−1={<1,0>,<2,0>,<3,0>,<2,1>,<3,1>,<3,2>}
11
设A={1,2...10}A=\{1,2...10\}A={1,2...10}
R={<x,y>∣x,y∈A∧x+y=10}R=\{<x,y>|x,y\in A\wedge x+y=10 \}R={<x,y>∣x,y∈A∧x+y=10}
对称性,非自反性(含<5,5><5,5><5,5>)
12
关系图:

关系矩阵:
[012301001100002110130010]\left[ \begin{matrix} & 0 & 1&2&3 \\ 0 &1&0&0&1 \\ 1&0&0&0&0 \\ 2&1&1&0&1\\ 3&0&0&1&0\\ \end{matrix} \right] 012301010100102000131010
16

$ 自反闭包:r®=R\cup R^0$
对称闭包:s(R)=R∪R−1对称闭包: s(R)=R\cup R^{-1}对称闭包:s(R)=R∪R−1
传递闭包:t(R)=R∪R2∪...传递闭包: t(R)=R\cup R^2\cup...传递闭包:t(R)=R∪R2∪...

18.1
是Z+Z^+Z+ 的划分
-
∅\emptyset∅ ∉\notin∈/ π\piπ
-
S1,S2不交
-
S2=Z+Z^+Z+-S1=Z+Z^+Z+∩\cap∩ ~S1
S1∪\cup∪S2=(Z+Z^+Z+∩\cap∩~S1)∪\cup∪S1=(Z+Z^+Z+∪\cup∪ S1)∩\cap∩(~S1∪\cup∪S1)=Z+Z^+Z+
20.2

22.1

极大元:e
极小元:a
最大元:e
最小元:a
23

蓝色圈住的地方为B
上界:12
下届:1
最小上届:12
最大下届:1
28
回答是否为满射、单射、双射。若为双射,求反函数。求A在f下的像f(A)
为满射,单射,双射。
反函数为f(x)−1=<x,x−1>f(x)^{-1}=<x,x-1>f(x)−1=<x,x−1>
f(A)=6
非满射,非单射。
f(A)={1,2}
非满射,为单射
f(A)={1,232\over 332}
34
(1)
g∘\circ∘f=f(g(x))=f(x+4)=(x+4)2−2(x+4)^2-2(x+4)2−2
f∘\circ∘g=g(f(x))=g(x2x^2x2-2)=x2x^2x2+2
(2)
g∘\circ∘f非单射,非满射,非双射
g∘\circ∘f非单射,非满射,非双射
(3)
g,h有反函数
g(x)−1g(x)^{-1}g(x)−1=x-4
h(x)−1h(x)^{-1}h(x)−1=(x+1)13(x+1)^{1\over3}(x+1)31
第五章 代数系统的一般概念
2判断二元运算是否封闭
(2) 封闭
(4) 封闭
(8) 封闭
3
(2)不符合交换律、适合结合律。不符合分配律,分配律是两个二元运算之间的
(4) 不符合交换律,符合结合律。不符合分配律,分配律是两个二元运算之间的
(8) 适合交换律、结合律。符合分配律,乘法对加法适合分配律
4
(2) 无单位元(仅右单位元1),无零元,显然可得,无逆元
(4) 单位元为nxn的单位矩阵,零元为nxn的零矩阵。有逆矩阵的矩阵A的逆元为A−1A^{-1}A−1
(8) 加法:无单位元,无零元,显然可得,无逆元 //乘法:单位元为1,无零元,无逆元
8
(1)
- 满足交换律:*、 ∘\circ∘、∙\bullet∙
- 满足结合律:*、∘\circ∘、∙\bullet∙ 、□\Box□
- 幂等:□\Box□
(2)
*:没有单位元,零元为a,无逆元
∘\circ∘: 单位元为a,无零元,a的逆元为a,b的逆元为b
∙\bullet∙ :无单位元,无零元,无逆元
□\Box□: 无单位元(左单位元为a),无零元(右零元为b),无逆元
11
(2) S2构成V的子代数,S2对+,∙\bullet∙ 都是封闭的
12
设V1=({1,2,3},°,1),其中x°y表示取x和y之中较大的数,V2=({5,6},*,6),其中x*y表示取x和y之中较小的数.
(1) 求出V1的所有子代数,其中哪些是平凡的子代数?哪些是真子代数?
(2)求积代数y,×y,给出积代数(V,×V,·,)的运算表和代数常数k,并说明k是什么特异元素
(1)
子代数系统的B的条件:
- B⊆\subseteq⊆S
- B∉\notin∈/ ∅\emptyset∅
- B和S含有相同的子代数常数
- B对V中所有运算封闭
1为单位元
B1={1},B2={1,2},B3={1,3},B4={1,2,3}
其中平凡子代数为:B1,B4
真子代数为:B2,B3
(2)
设V1×V2=<S1×S2,∙,k>V_1\times V_2=<S1\times S2,\bullet,k>V1×V2=<S1×S2,∙,k>
S1×S2={<1,5>,<1,6>,<2,5>,<2,6>,<3,5>,<3.6>}S_1\times S_2=\{<1,5>,<1,6>,<2,5>,<2,6>,<3,5>,<3.6>\}S1×S2={<1,5>,<1,6>,<2,5>,<2,6>,<3,5>,<3.6>}
<x1,y1>,<x2,y2>∈S1×S2<x_1,y_1>,<x_2,y_2>\in S_1\times S_2<x1,y1>,<x2,y2>∈S1×S2
<x1,y1>∙<x2,y2>=<x1∘x2,y1∗y2><x_1,y_1>\bullet<x_2,y_2>=<x1\circ x_2,y_1*y_2><x1,y1>∙<x2,y2>=<x1∘x2,y1∗y2>
运算表:
[<1,5><1,6><2,5><2,6><3,5><3.6><1,5><1,5><1,5><2,5><2,5><3,5><3,5><1,6><1,5><1,6><2,5><2,6><3,5><3,6><2,5><2,5><2,5><2,5><2,5><3,5><3,5><2,6><2,5><2,6><2,5><2,6><3,5><3,6><3,5><3,5><3,5><3,5><3,5><3,5><3,5><3,6><3,5><3,6><3,5><3,6><3,5><3,6>]\left[ \begin{matrix} &<1,5>&<1,6>&<2,5>&<2,6>&<3,5>&<3.6>\\ <1,5>&<1,5>&<1,5>&<2,5>&<2,5>&<3,5>&<3,5>\\ <1,6>&<1,5>&<1,6>&<2,5>&<2,6>&<3,5>&<3,6>\\ <2,5>&<2,5>&<2,5>&<2,5>&<2,5>&<3,5>&<3,5>\\ <2,6>&<2,5>&<2,6>&<2,5>&<2,6>&<3,5>&<3,6>\\ <3,5>&<3,5>&<3,5>&<3,5>&<3,5>&<3,5>&<3,5>\\ <3,6>&<3,5>&<3,6>&<3,5>&<3,6>&<3,5>&<3,6>\\ \end{matrix} \right] <1,5><1,6><2,5><2,6><3,5><3,6><1,5><1,5><1,5><2,5><2,5><3,5><3,5><1,6><1,5><1,6><2,5><2,6><3,5><3,6><2,5><2,5><2,5><2,5><2,5><3,5><3,5><2,6><2,5><2,6><2,5><2,6><3,5><3,6><3,5><3,5><3,5><3,5><3,5><3,5><3,5><3.6><3,5><3,6><3,5><3,6><3,5><3,6>
k=<1,6>k=<1,6>k=<1,6>
k是单位元
14
若ψ为V1到V2的同态V1=<S1,∘>(V)2=<S2,∗>则ψ(x∘y)=ψ(x)∗ψ(y)普通加法和矩阵加法ψ(a)=[a00a]ψ(bi)=[0b−b0]ψ(a)+ψ(b)=[ab−ba](+为矩阵加法)故可知ψ(a+bi)=ψ(a)+ψ(bi)(第一个+为普通加法,第二个为矩阵加)若\psi为V_1到V_2的同态\\ V1=<S_1,\circ>\pod V_2=<S_2,*>\\ 则\psi(x\circ y)=\psi(x)*\psi(y)\\ 普通加法和矩阵加法\\ \psi(a)=\left[ \begin{matrix} a&0\\ 0&a \end{matrix} \right] \psi(bi)=\left[ \begin{matrix} 0&b\\ -b&0 \end{matrix} \right]\\ \psi(a)+\psi(b)=\left[ \begin{matrix} a&b\\ -b&a \end{matrix} \right](+为矩阵加法)\\ 故可知\psi(a+bi)=\psi(a)+\psi(bi)(第一个+为普通加法,第二个为矩阵加)\\ 若ψ为V1到V2的同态V1=<S1,∘>(V)2=<S2,∗>则ψ(x∘y)=ψ(x)∗ψ(y)普通加法和矩阵加法ψ(a)=[a00a]ψ(bi)=[0−bb0]ψ(a)+ψ(b)=[a−bba](+为矩阵加法)故可知ψ(a+bi)=ψ(a)+ψ(bi)(第一个+为普通加法,第二个为矩阵加)
普通乘法和矩阵乘法ψ(a∗bi)=[0a∗b−a∗b0]ψ(a)=[a00a]ψ(bi)=[0b−b0]ψ(a)∗ψ(b)=[0a∗b−a∗b0]可知ψ(a∗bi)=ψ(a)∗ψ(bi)(第一个∗为普通乘法,第二个∗为矩阵乘法)普通乘法和矩阵乘法\\ \psi(a*bi)=\left[ \begin{matrix} 0&a*b\\ -a*b&0 \end{matrix} \right]\\ \psi(a)=\left[ \begin{matrix} a&0\\ 0&a \end{matrix} \right]\\ \psi(bi)=\left[ \begin{matrix} 0&b\\ -b&0 \end{matrix} \right]\\ \psi(a)*\psi(b)=\left[ \begin{matrix} 0&a*b\\ -a*b&0\\ \end{matrix} \right]\\ 可知\psi(a*bi)=\psi(a)*\psi(bi)(第一个*为普通乘法,第二个*为矩阵乘法) 普通乘法和矩阵乘法ψ(a∗bi)=[0−a∗ba∗b0]ψ(a)=[a00a]ψ(bi)=[0−bb0]ψ(a)∗ψ(b)=[0−a∗ba∗b0]可知ψ(a∗bi)=ψ(a)∗ψ(bi)(第一个∗为普通乘法,第二个∗为矩阵乘法)
故可知ψ\psiψ为V1到V2V_1到V_2V1到V2的同态
不为单同态,因为对于*来说,<a,b>和<b,a>的结果相同ψ(a∗bi)=ψ(a)∗ψ(bi)=ψ(b∗ai)<a,b>和<b,a>的结果相同\psi(a*bi)=\psi(a)*\psi(bi)=\psi(b*ai)<a,b>和<b,a>的结果相同ψ(a∗bi)=ψ(a)∗ψ(bi)=ψ(b∗ai)
为满同态
不为同构
第六章 几个典型的代数系统
1.
(1)可结合、1为单位元、其中任何元素都有逆元。故为群
(4)lcm:最小公倍数 gcd:最大公约数。
可结合。对于lcm有单位元1,对gcd有零元1。在S不仅只有一个元素时,零元无逆元。故为半群
(5)可结合。单位元为0。0的逆元为0,1的逆元为1;故其中任何元素都有逆元。为群
5.
可结合。2为单位元。其中任何元素都有逆元,为4-x。故可构成群
6.
(1)给出∘\circ∘运算表
| ∘\circ∘ | f1=x | f2=x−1x^{-1}x−1 | f3=1-x | f4=(1−x)−1(1-x)^{-1}(1−x)−1 | f5=(x−1)x−1(x-1)x^{-1}(x−1)x−1 | f6=x(x−1)−1x(x-1)^{-1}x(x−1)−1 |
|---|---|---|---|---|---|---|
| f1=x | x | x−1x^{-1}x−1 | 1-x | (1−x)−1(1-x)^{-1}(1−x)−1 | (x−1)x−1(x-1)x^{-1}(x−1)x−1 | x(x−1)−1x(x-1)^{-1}x(x−1)−1 |
| f2=x−1x^{-1}x−1 | x−1x^{-1}x−1 | x | 1-x−1x^{-1}x−1 | (1−x−1)−1(1-x^{-1})^{-1}(1−x−1)−1 | (x−1−1)x(x^{-1}-1)x(x−1−1)x | x−1(x−1−1)−1x^{-1}(x^{-1}-1)^{-1}x−1(x−1−1)−1 |
| f3=1-x | 1-x | (1−x)−1(1-x)^{-1}(1−x)−1 | x | x−1x^{-1}x−1 | −1-1−1 | -1 |
| f4=(1−x)−1(1-x)^{-1}(1−x)−1 | (1−x)−1(1-x)^{-1}(1−x)−1 | 1-x | 1−(1−x)−11-(1-x)^{-1}1−(1−x)−1 | (1−(1−x)−1)−1(1-(1-x)^{-1})^{-1}(1−(1−x)−1)−1 | x | (1−x)−1((1−x)−1−1)−1(1-x)^{-1}((1-x)^{-1}-1)^{-1}(1−x)−1((1−x)−1−1)−1 |
| f5=(x−1)x−1(x-1)x^{-1}(x−1)x−1 | (x−1)x−1(x-1)x^{-1}(x−1)x−1 | (x−1)−1x(x-1)^{-1}x(x−1)−1x | 1−(x−1)x−11-(x-1)x^{-1}1−(x−1)x−1 | x | ((x−1)x−1−1)(x−1)−1x((x-1)x^{-1}-1)(x-1)^{-1}x((x−1)x−1−1)(x−1)−1x | (x−1)x−1((x−1)x−1−1)−1(x-1)x^{-1}((x-1)x^{-1}-1)^{-1}(x−1)x−1((x−1)x−1−1)−1 |
| f6=x(x−1)−1x(x-1)^{-1}x(x−1)−1 | x(x−1)−1x(x-1)^{-1}x(x−1)−1 | x−1(x−1)x^{-1}(x-1)x−1(x−1) | 1−x(x−1)−11-x(x-1)^{-1}1−x(x−1)−1 | (1−x(x−1)−1)−1(1-x(x-1)^{-1})^{-1}(1−x(x−1)−1)−1 | (x(x−1)−1−1)x−1(x−1)(x(x-1)^{-1}-1)x^{-1}(x-1)(x(x−1)−1−1)x−1(x−1) | x |
可结合。f1为其单位元,所以元素都有逆元。故<F,∘><F,\circ><F,∘> 是一个群
7.
(1)可结合,a为单位元,所有元素均有逆元。故<G,∘><G,\circ><G,∘> 为群
(2)生成元有b,c。因为bk,ckb^{k},c^{k}bk,ck涵盖了G里的所有元素
11.
G={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19}G=\{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19\}G={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19}
(1)所有生成元为:
n=20,生成元为小于等于20且与20互质的数
1 3 7 9 11 13 17 19
(2)G的所有子群
G=<1>=<3>=<7>=<9>=<11>=<13>=<17>=<19>G=<1>=<3>=<7>=<9>=<11>=<13>=<17>=<19>G=<1>=<3>=<7>=<9>=<11>=<13>=<17>=<19>(生成元的生成子群=G)
20的正因子为 1 2 4 5 10 20,故有6个子群
H1=<0>={0}H1=<0>=\{0\}H1=<0>={0}
H2=<1>=GH2=<1>=GH2=<1>=G
H3=<2>={0,2,4,6,8,10,12,14,16,18}=<20−2>=<18>H3=<2>=\{0,2,4,6,8,10,12,14,16,18\}=<20-2>=<18>H3=<2>={0,2,4,6,8,10,12,14,16,18}=<20−2>=<18>
H4=<4>={0,4,8,12,16}=<20−4>=<16>H4=<4>=\{0,4,8,12,16\}=<20-4>=<16>H4=<4>={0,4,8,12,16}=<20−4>=<16>
H5=<5>={0,5,10,15}=<15>H5=<5>=\{0,5,10,15\}=<15>H5=<5>={0,5,10,15}=<15>
H6=<10>={0,10}H6=<10>=\{0,10\}H6=<10>={0,10}
(3)[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FJb3ITaF-1678012348161)(课外学习资料/所需图片/QQ截图20221205145804.png)]
12
(1)
σ=\sigma=σ=(1 4 6 2 5 3 ),τ\tauτ=(1 3 2)(4 5 6)
(2)
στ−1σ=(1,2,6)(3,5,4)\sigma\tau^{-1}\sigma=(1,2,6)(3,5,4)στ−1σ=(1,2,6)(3,5,4)
σ2=(1,6,5)(2,3,4)\sigma^2=(1,6,5)(2,3,4)σ2=(1,6,5)(2,3,4)
(3)
σ\sigmaσ是6阶轮换,τ\tauτ是3阶轮换
15
(1)
由于已知为布尔代数,∨\vee∨对∧\wedge∧有可分配,∧\wedge∧对∨\vee∨也可分配
(a∧\wedge∧b)∨\vee∨(a∧\wedge∧b∧\wedge∧c)∨\vee∨(b∧\wedge∧c)∨\vee∨(a∧\wedge∧b∧\wedge∧c)
=((a∧\wedge∧b)∧\wedge∧(1∨\vee∨c))∨\vee∨((b∧\wedge∧c)∧\wedge∧(1∨\vee∨a))
=(a∧\wedge∧b)∨\vee∨(b∧\wedge∧c)
=b∧\wedge∧(a∨\vee∨c)
(2)
f∗f^*f∗=b∨\vee∨(a∧\wedge∧c)
16

18
根据 ∨\vee∨对∧\wedge∧的分配律可得
a∨\vee∨(b∧\wedge∧c)=(a∨\vee∨b)∧\wedge∧(a∨\vee∨c)
又因为a《=c,故a∨\vee∨c=c
带入可得
a∨\vee∨(b∧\wedge∧c)=(a∨\vee∨b)∧\wedge∧(a∨\vee∨c)=(a∨\vee∨b)∧\wedge∧c
第七章 图的基本概念
1
(1)
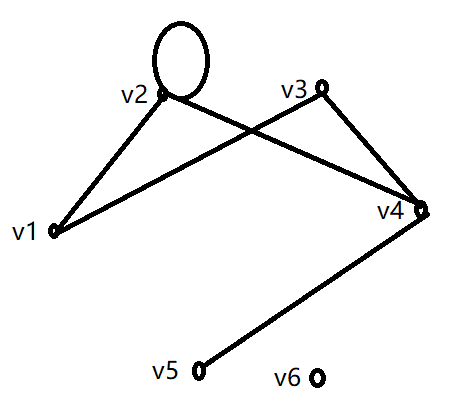
(2)
d(v1)=2
d(v2)=4
d(v3)=2
d(v4)=3
d(v5)=1
d(v6)=0
∑i=16d(vi)=2+4+2+3+1+0=12=2∗6=2∗m\stackrel{6}{\underset{i=1}{\sum}}d(v_i)=2+4+2+3+1+0=12=2*6=2*mi=1∑6d(vi)=2+4+2+3+1+0=12=2∗6=2∗m
(3)
奇度顶点的个数为2个。验证了:在任何图中,度数为奇数的顶点个数是偶数
(4)
无平行边。环为e2e_2e2 。孤立点为v6v_6v6 。悬挂顶点为v5v_5v5 。悬挂边为e4e_4e4
(5)
多重图:含平行边
简单图:不含平行边也不含环
G无平行边,G不是多重图。G含环,G不是简单图
2
由握手定理。∑i=16d(vi)=2∗m=24\stackrel{6}{\underset{i=1}{\sum}}d(v_i)=2*m=24i=1∑6d(vi)=2∗m=24。减去3*6度,还剩下6度,若剩下n-3个顶点均为2度时,n最小。计算可得G中至少有6个顶点
4
设:n阶无向图中,度数为k+1的顶点个数为x,度数为k的顶点个数为y。
由题可得
x+y=n
根据握手定理得
(k+1)*x+k*y=2*m
(k+1)*(x+y)-y=2*m
(k+1)*n-y=2*m
y=(k+1)*n-2*m
7
(1)
4阶自补图有一种非同构
5阶自补图有两种非同构
(2)
不存在3阶自补图:
3阶完全图一共有3条边。其生成子图,与其生成子图的补图,边数不同,不可能同构。
不存在6阶自补图:
6阶完全图一共有6*5/2=15条边。其生成子图,与其生成子图的补图,边数不同,不可能同构。
9
n为奇数,则n阶完全图每个顶点的度数为偶数。
若G中viv_ivi 的度数为奇数。根据补图的定义可得dG(vi)+dGˉ(vi)=dkn(vi)d_G(vi)+d_{\bar G}(v_i)=d_{k_n}(v_i)dG(vi)+dGˉ(vi)=dkn(vi) ,n阶完全图每个顶点的度数为偶数。则若Gˉ\bar GGˉ中viv_ivi 的度数为奇数。同理可推广至其他的点
可证,G与G的补图的奇度顶点的个数相等
11
(1)
4条不同的初级回路:ce3c,ee2de1e,bde1eb,baebce_3c,ee_2de_1e,bde_1eb,baebce3c,ee2de1e,bde1eb,baeb
5条不同的简单回路:ce3c,ede,bdeb,beab,baedebce_3c,ede,bdeb,beab,baedebce3c,ede,bdeb,beab,baedeb
(2)
a到d的短程线为:aee2daee_2daee2d,距离为d<a,d>=2d<a,d>=2d<a,d>=2
(3)
d到a的短程线为:de1ebade_1ebade1eba,距离为d<d,a>=3d<d,a>=3d<d,a>=3
(4)
D是单向连通图
经过每个顶点至少一次的通路:baee2dcbaee_2dcbaee2dc
12
D的邻接矩阵为
A1=[0100001111011000]A^1=\left[ \begin{matrix} 0&1&0&0\\ 0&0&1&1\\ 1&1&0&1\\ 1&0&0&0\\ \end{matrix} \right] A1=0011101001000110
A2=[0011210111110100]A^2=\left[ \begin{matrix} 0&0&1&1\\ 2&1&0&1\\ 1&1&1&1\\ 0&1&0&0\\ \end{matrix} \right] A2=0210011110101110
A3=[2101121122120011]A^3=\left[ \begin{matrix} 2&1&0&1\\ 1&2&1&1\\ 2&2&1&2\\ 0&0&1&1\\ \end{matrix} \right] A3=2120122001111121
A4=[1211222333232101]A^4=\left[ \begin{matrix} 1&2&1&1\\ 2&2&2&3\\ 3&3&2&3\\ 2&1&0&1\\ \end{matrix} \right] A4=1232223112201331
(1)
D中v1v_1v1到v4v_4v4长度为4的通路有多少条?
a14(4)=2a_{14}^{(4)}=2a14(4)=2,有两条
(2)
D中v1v_1v1到v1v_1v1长度为4的通路有多少条?
a11(3)=2a_{11}^{(3)}=2a11(3)=2,有两条
(3)
D中长度为4通路总数为多少?其中有多少条是回路?
总数为∑i,j4aij(4)=29\stackrel{4}{\underset{i,j}{\sum}}a_{ij}^{(4)}=29i,j∑4aij(4)=29条通路
其中∑i,j4aii(4)=6\stackrel{4}{\underset{i,j}{\sum}}a_{ii}^{(4)}=6i,j∑4aii(4)=6条为回路
15
正则图为无向简单图,不可有平行边和环
有2种非同构情况
6和3,3
相关文章:

xmu 离散数学 卢杨班作业详解【4-7章】
文章目录第四章 二元关系和函数4.6.2911121618.120.222.1232834第五章 代数系统的一般概念2判断二元运算是否封闭348111214第六章 几个典型的代数系统1.5.6.7.11.12151618第七章 图的基本概念12479111215第四章 二元关系和函数 4. A{1,2,3} 恒等关系 IA{<1,1>,<2,2…...

多重背包问题中的二进制状态压缩
1.多重背包问题 经典的多重背包问题和01背包问题的相似之处在于二者的一维遍历顺序都是从右侧往左侧遍历。 同时多重背包的一维写法不比二维写法降低时间复杂度。 2.多重背包标准写法:(平铺展开形式) class Solution {public int maxValue(int N, int C, int[] s…...

汇编语言程序设计(四)之汇编指令
系列文章 汇编语言程序设计(一) 汇编语言程序设计(二)之寄存器 汇编语言程序设计(三)之汇编程序 汇编指令 1. 数据传输指令 指令包括:MOV、XCHG、XLAT、LEA、LDS、LES、PUSH、POP、PUSHF、LA…...

Vant2 源码分析之 vant-sticky
前言 原打算借鉴 vant-sticky 源码,实现业务需求的某个功能,第一眼看以为看懂了,拿来用的时候,才发现一知半解。看第二遍时,对不起,是我肤浅了。这里侧重分析实现原理,其他部分不拓展开来&…...
【自然语言处理】【大模型】大语言模型BLOOM推理工具测试
相关博客 【自然语言处理】【大模型】大语言模型BLOOM推理工具测试 【自然语言处理】【大模型】GLM-130B:一个开源双语预训练语言模型 【自然语言处理】【大模型】用于大型Transformer的8-bit矩阵乘法介绍 【自然语言处理】【大模型】BLOOM:一个176B参数…...
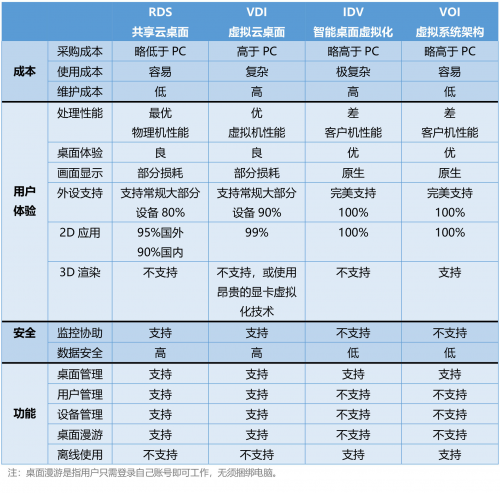
云桌面技术初识:VDI,IDV,VOI,RDS
VDI(Virtual Desktop Infrastucture,虚拟桌面架构),俗称虚拟云桌面 VDI构架采用的“集中存储、集中运算”构架,所有的桌面以虚拟机的方式运行在服务器硬件虚拟化层上,桌面以图像传输的方式发送到客户端。 …...

基于本地centos构建gdal2.4.4镜像
1.前言 基于基础镜像构建gdal环境一般特别大,一般少则1.6G,多则2G甚至更大,这对于镜像的迁移造成了极大的不便。究其原因在于容器中有大量的源码文件以及编译中间过程文件,还要大量编译需要的yum库。本文主要通过在centos系统上先…...

生产环境线程问题排查
线程状态的解读RUNNABLE线程处于运行状态,不一定消耗CPU。例如,线程从网络读取数据,大多数时间是挂起的,只有数据到达时才会重新唤起进入执行状态。只有Java代码显式调用sleep或wait方法时,虚拟机才可以精准获取到线程…...

Day908.joinsnljdist和group问题和备库自增主键问题 -MySQL实战
join&snlj&dist和group问题和备库自增主键问题 Hi,我是阿昌,今天学习记录的是关于join&snlj&dist和group问题和备库自增主键问题的内容。 一、join 的写法 join 语句怎么优化?中,在介绍 join 执行顺序的时候&am…...

算法 - 剑指Offer 丑数
题目 我们把只包含质因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。 解题思路 这题我使用最简单方法去做, 首先我们可以获取所有2n,3n,5*n的丑数,只是我们这里暂时无法排序,并且可能…...
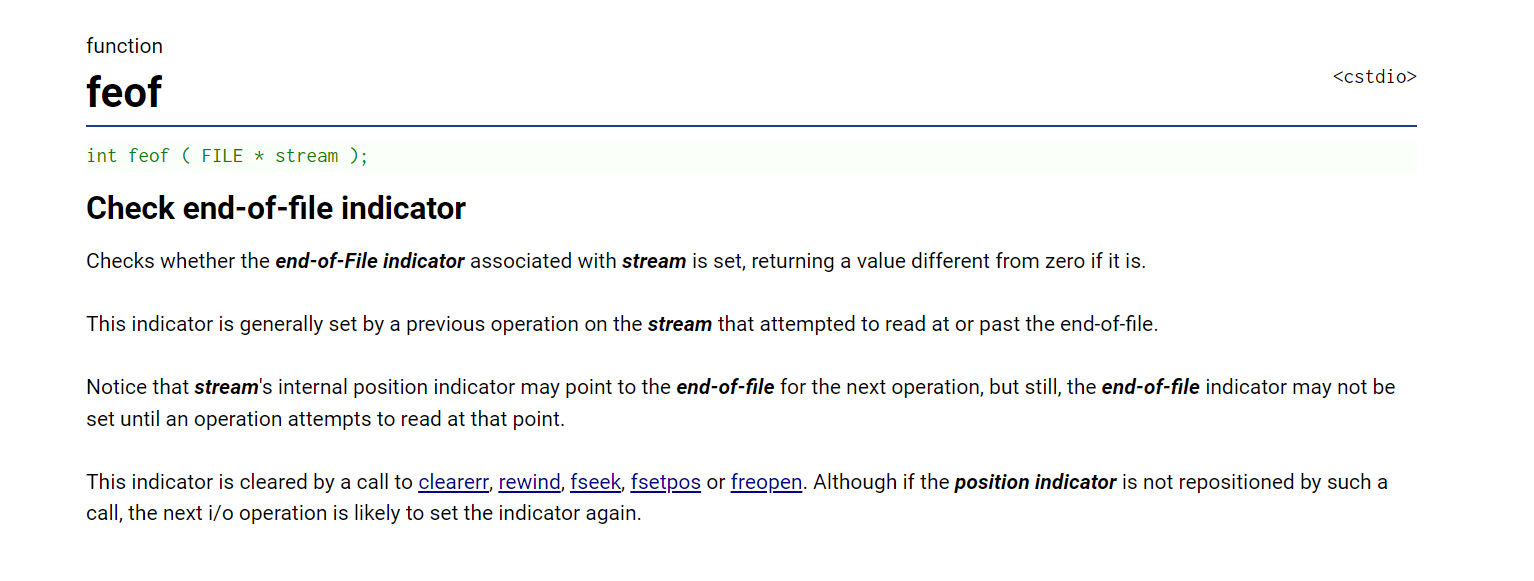
【ONE·C || 文件操作】
总言 C语言:文件操作。 文章目录总言1、文件是什么?为什么需要文件?1.1、为什么需要文件?1.2、文件是什么?2、文件的打开与关闭2.1、文件指针2.2、文件打开和关闭:fopen、fclose2.3、文件使用方式3、文…...
cmd窗口中java命令报错。错误:找不到或无法加载主类 java的jdk安装过程中踩过的坑
错误: 找不到或无法加载主类 HelloWorld 遇到这个问题时,我尝试过网上其他人的做法。有试过添加classpath,也有试过删除classpath。但是依然报错,这里javac可以编译通过,说明代码应该是没有问题的。只是在运行是出现了错误。我安装…...
)
Breathwork(呼吸练习)
查了下呼吸练习相关内容,做个记录。我又在油管学习啦。 喜欢在you. tube看一些self-help相关的内容。比如学习方法、拉伸、跑步、力量举、自重锻炼等等。 总是听Obi Vicent说起Breathwork,比如: My 6am Morning Routine | New Healthy Habit…...
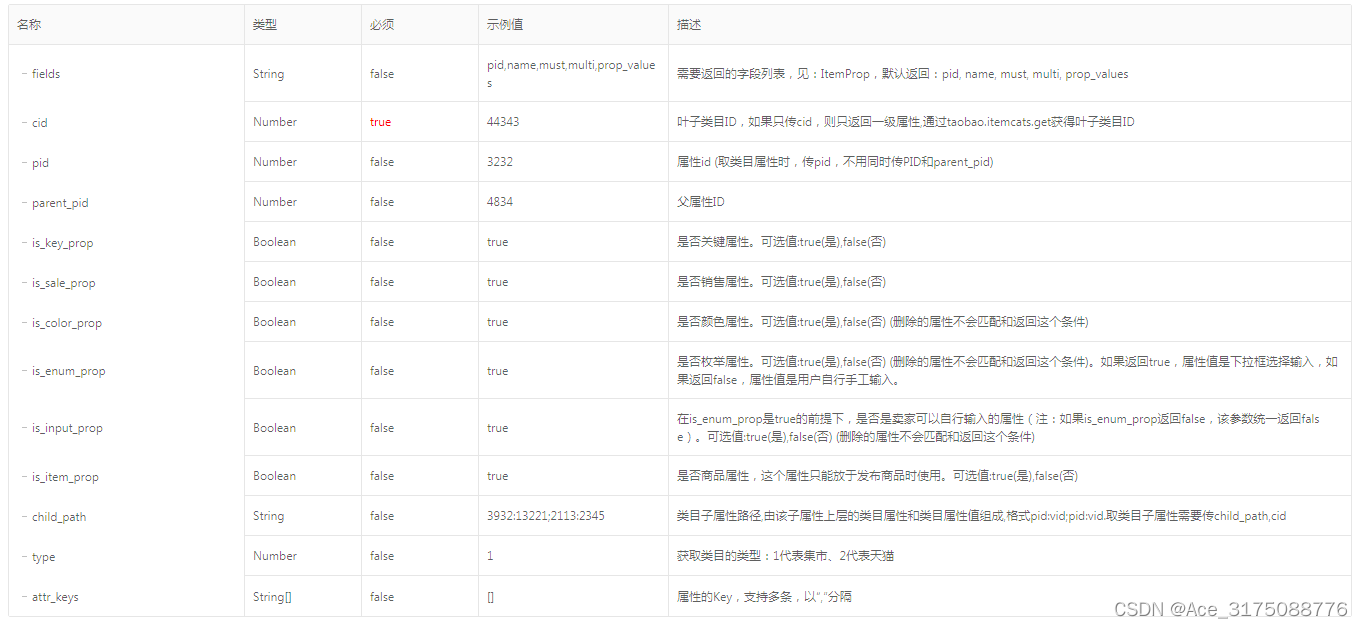
taobao.itemprops.get( 获取标准商品类目属性 )
¥开放平台基础API不需用户授权 通过设置必要的参数,来获取商品后台标准类目属性,以及这些属性里面详细的属性值prop_values。 公共参数 请求地址: HTTP地址 http://gw.api.taobao.com/router/rest 公共请求参数: 公共响应参数: 请求参数 点…...
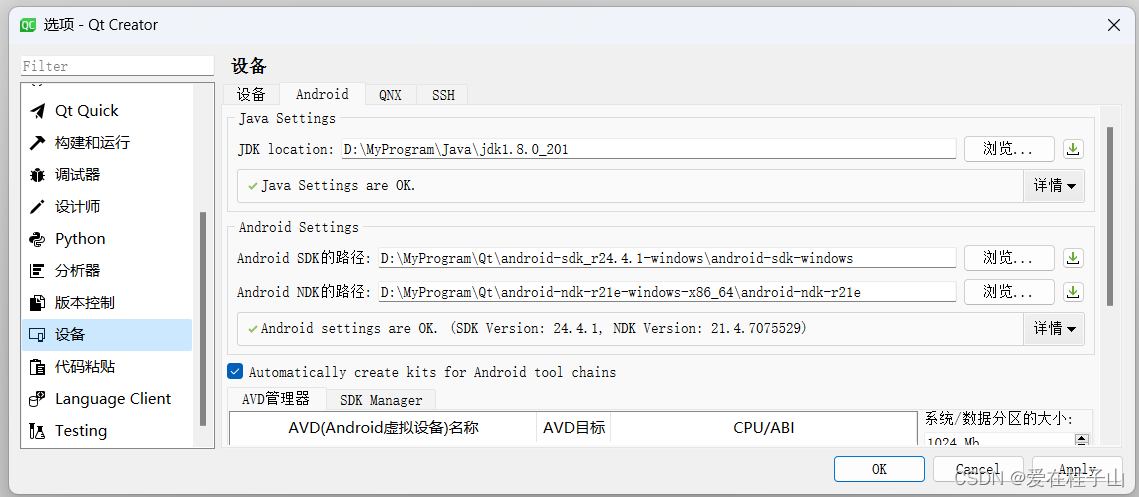
QT配置安卓环境(保姆级教程)
目录 下载环境资源 JDK1.8 NDK SDK 安装QT 配置环境 下载环境资源 JDK1.8 介绍JDK是Java开发的核心工具,为Java开发者提供了一套完整的开发环境,包括开发工具、类库和API等,使得开发者可以高效地编写、测试和运行Java应用程序。 下载…...
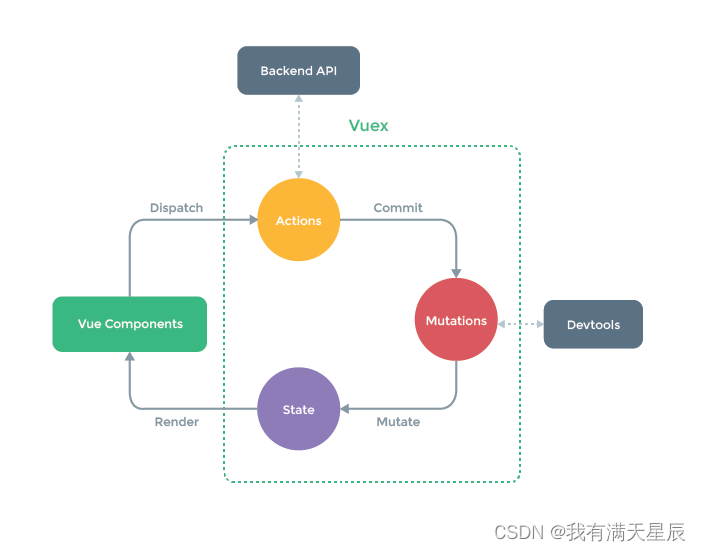
【uni-app教程】八、UniAPP Vuex 状态管理
八、UniAPP Vuex 状态管理 概念 Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式。它采用集中式存储管理应用的所有组件的状态,并以相应的规则保证状态以一种可预测的方式发生变化。 应用场景 Vue多个组件之间需要共享数据或状态。 关键规则 State:…...
)
同花顺测试面经(30min)
大概三十分钟,面试官人还挺好的 1.自我介绍 2.详细问你了自我介绍中的一个实习经历 3.对我们公司有什么了解 !!(高频) 4.对测试有什么看法,为什么选测试 5.黑盒白盒分别是什么 6.对测试左移有什么看法…...

C++-简述#ifdef、#else、#endif和#ifndef的作用
回答如下: #ifdef,#else,#endif和#ifndef都是预处理指令,用于条件编译。#ifdef:这个指令用来判断一个宏是否已经被定义过,如果已经定义过,则执行后面的代码块。#else:这个指令一般与…...

VictoriaMetrics 集群部署
官网 ## 官网 https://github.com/VictoriaMetrics/VictoriaMetrics 集群角色详解 VictoriaMetrics 集群模式。主要由 vmstorage ,vminsert,vmselect 三部分组成,这三个组件每个组件都可以单独进行扩展。其中: vmstorage 负责提供数据存储服务vminsert 是数据存…...
【基于感知损失的无监督泛锐化】
PercepPan: Towards Unsupervised Pan-Sharpening Based on Perceptual Loss (PercepPan:基于感知损失的无监督泛锐化) 在基于神经网络的全色锐化文献中,作为地面实况标签的高分辨率多光谱图像通常是不可用的。为了解决这个问题…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
