【数据结构】AVL平衡二叉树底层原理以及二叉树的演进之多叉树
1.AVL平衡二叉树底层原理
-
背景
-
二叉查找树左右子树极度不平衡,退化成为链表时候,相当于全表扫描,时间复杂度就变为了O(n)
-
插入速度没影响,但是查询速度变慢,比单链表都慢,每次都要判断左右子树是否为空
-
需要保证二叉查找树一直保持平衡,就需要用到平衡二叉树
-

-
平衡二叉树
- 称为AVL树(Adelson-Velskii和Landis)平衡二叉查找树是一种特殊的二叉查找树每个节点的左右子树的高度差不能超过1。
- 平衡二叉树保证了树的构造是平衡的,当插入或删除数据导致不满足平衡二叉树不平衡时,会进行调整树上的节点来保持平衡。
-
平衡二叉树的插入和删除操作都是O(logn)的,因此它的查找性能很高,比非平衡的二叉查找树要快得多。
-
实现方式:红黑树、 Treap、伸展树等。
-
核心思想
-
在插入或删除节点时,如果发现子树不平衡,则对子树进行旋转操作,使其重新达到平衡
-
旋转操作有三种,哪边高度底就哪边旋转, 提升高度
- 左旋LL旋转
- 右旋RR旋转
- 左右LR双旋 和 右左RL双旋
-
-
图解过程




-
问题点
-
查找操作
- 二叉搜索树的时间复杂度介于O(log2N)到O(n)之间
- 如果退化成单链表,时间复杂度就是顺序查找,为O(n)
- 如果是平衡二叉树,查找效率会提高到O(log2N)
-
例子
- 平衡二叉树的高度就等于每次查询数据时磁盘 IO 操作的次数。
- 假如磁盘每次寻道时间为10ms,在表数据量大时,查询性能就会很差
- 1百万的数据量,log2(N)约等于20次磁盘IO,时间20*10=0.2s
- log2(N) 相当于2的多少次方(立方)等于N,例:log2 (8)= 3
- 2的20次方=1048576,所以就是20次磁盘IO
-
不支持范围查询快速查找,范围查询时需要从根节点多次遍历,查询效率比较低
-
2.二叉树的演进之多叉树
-
背景
-
平衡二叉树操作效率高,但是存在不少问题,常规需要把树加载到内存里面
-
如果节点少则没问题,但是如果节点多 则高度很大,进行IO操作则存在性能问题
-
场景
- 平衡二叉树每个节点只存储一个键值和数据的,每个磁盘块仅仅存储一个键值和数据
- 如果要存储海量的数据,那构建平衡二叉树的时候耗时多
- 如果平衡二叉树的节点将会非常多,高度也会极其高,查找数据时会进行很多次磁盘 IO,效率将会极低
-
为了解决平衡二叉树的这个问题,设计一种单个节点可以存储多个键值和数据的平衡树,也就是我们接下来要说的 多叉树
-
-
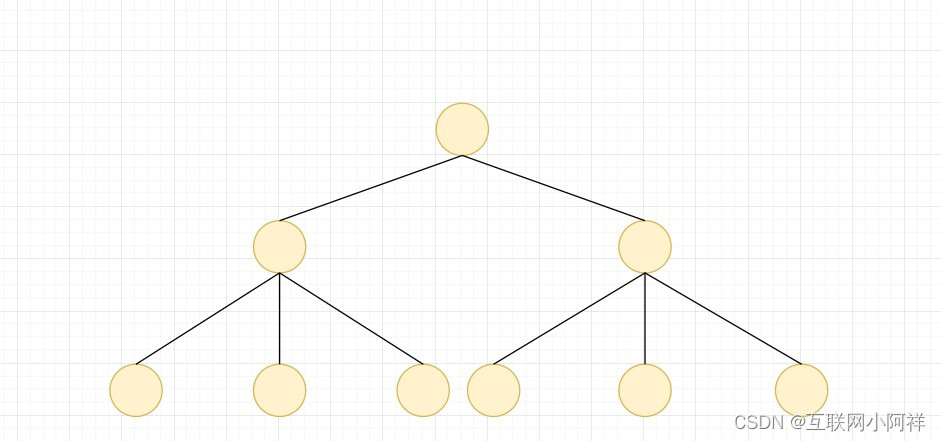
多叉树
-
也叫 多路查找树(muitl-way search tree)
-
每一个节点的子树可以多于两个,且每一个节点处可以存储多个元素,常见的就是B树、B+树等
- 注意:B是Balanced意思,不是Binary的意思
-
多叉树通过重新组织节点,降低了树的高度,可以提高IO效率
-
-
应用
-
操作系统IO操作都会利用磁盘预读原理,如果一个节点大小是一个存储页(4KB)
-
存储每个节点只需要一次IO即可完成存储
-
B树在存储系统里面广泛应用,比如数据库系统、文件系统等
都会利用磁盘预读原理,如果一个节点大小是一个存储页(4KB) -
存储每个节点只需要一次IO即可完成存储
-
B树在存储系统里面广泛应用,比如数据库系统、文件系统等
-
具体多叉树的应用及原理B-Tree和B+Tree的底层逻辑会在 MySQL底层存储B-Tree和B+Tree原理分析 中解释说明
-
相关文章:

【数据结构】AVL平衡二叉树底层原理以及二叉树的演进之多叉树
1.AVL平衡二叉树底层原理 背景 二叉查找树左右子树极度不平衡,退化成为链表时候,相当于全表扫描,时间复杂度就变为了O(n) 插入速度没影响,但是查询速度变慢,比单链表都慢,每次都要判断左右子树是否为空 需…...

K8S篇-安装nfs插件
前言 有关k8s的搭建可以参考:http://t.csdn.cn/H84Zu 有关过程中使用到的nfs相关的nas,可以参考: http://t.csdn.cn/ACfoT http://t.csdn.cn/tPotK http://t.csdn.cn/JIn27 安装nfs存储插件 NFS-Subdir-External-Provisioner是一个自动配置…...
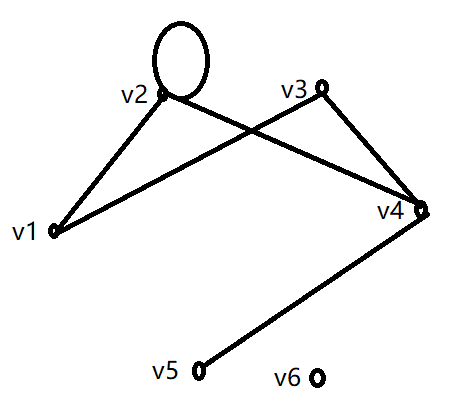
xmu 离散数学 卢杨班作业详解【4-7章】
文章目录第四章 二元关系和函数4.6.2911121618.120.222.1232834第五章 代数系统的一般概念2判断二元运算是否封闭348111214第六章 几个典型的代数系统1.5.6.7.11.12151618第七章 图的基本概念12479111215第四章 二元关系和函数 4. A{1,2,3} 恒等关系 IA{<1,1>,<2,2…...

多重背包问题中的二进制状态压缩
1.多重背包问题 经典的多重背包问题和01背包问题的相似之处在于二者的一维遍历顺序都是从右侧往左侧遍历。 同时多重背包的一维写法不比二维写法降低时间复杂度。 2.多重背包标准写法:(平铺展开形式) class Solution {public int maxValue(int N, int C, int[] s…...

汇编语言程序设计(四)之汇编指令
系列文章 汇编语言程序设计(一) 汇编语言程序设计(二)之寄存器 汇编语言程序设计(三)之汇编程序 汇编指令 1. 数据传输指令 指令包括:MOV、XCHG、XLAT、LEA、LDS、LES、PUSH、POP、PUSHF、LA…...

Vant2 源码分析之 vant-sticky
前言 原打算借鉴 vant-sticky 源码,实现业务需求的某个功能,第一眼看以为看懂了,拿来用的时候,才发现一知半解。看第二遍时,对不起,是我肤浅了。这里侧重分析实现原理,其他部分不拓展开来&…...
【自然语言处理】【大模型】大语言模型BLOOM推理工具测试
相关博客 【自然语言处理】【大模型】大语言模型BLOOM推理工具测试 【自然语言处理】【大模型】GLM-130B:一个开源双语预训练语言模型 【自然语言处理】【大模型】用于大型Transformer的8-bit矩阵乘法介绍 【自然语言处理】【大模型】BLOOM:一个176B参数…...
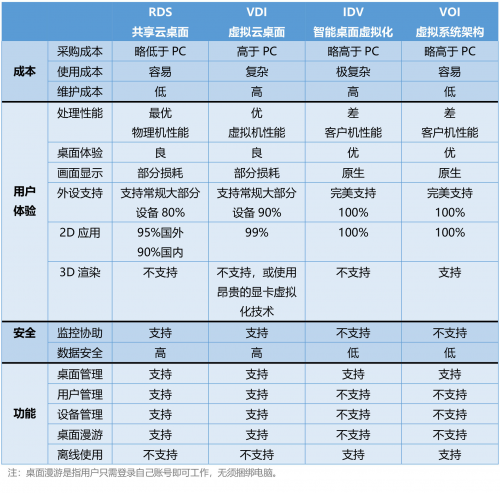
云桌面技术初识:VDI,IDV,VOI,RDS
VDI(Virtual Desktop Infrastucture,虚拟桌面架构),俗称虚拟云桌面 VDI构架采用的“集中存储、集中运算”构架,所有的桌面以虚拟机的方式运行在服务器硬件虚拟化层上,桌面以图像传输的方式发送到客户端。 …...

基于本地centos构建gdal2.4.4镜像
1.前言 基于基础镜像构建gdal环境一般特别大,一般少则1.6G,多则2G甚至更大,这对于镜像的迁移造成了极大的不便。究其原因在于容器中有大量的源码文件以及编译中间过程文件,还要大量编译需要的yum库。本文主要通过在centos系统上先…...

生产环境线程问题排查
线程状态的解读RUNNABLE线程处于运行状态,不一定消耗CPU。例如,线程从网络读取数据,大多数时间是挂起的,只有数据到达时才会重新唤起进入执行状态。只有Java代码显式调用sleep或wait方法时,虚拟机才可以精准获取到线程…...

Day908.joinsnljdist和group问题和备库自增主键问题 -MySQL实战
join&snlj&dist和group问题和备库自增主键问题 Hi,我是阿昌,今天学习记录的是关于join&snlj&dist和group问题和备库自增主键问题的内容。 一、join 的写法 join 语句怎么优化?中,在介绍 join 执行顺序的时候&am…...

算法 - 剑指Offer 丑数
题目 我们把只包含质因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。 解题思路 这题我使用最简单方法去做, 首先我们可以获取所有2n,3n,5*n的丑数,只是我们这里暂时无法排序,并且可能…...
【ONE·C || 文件操作】
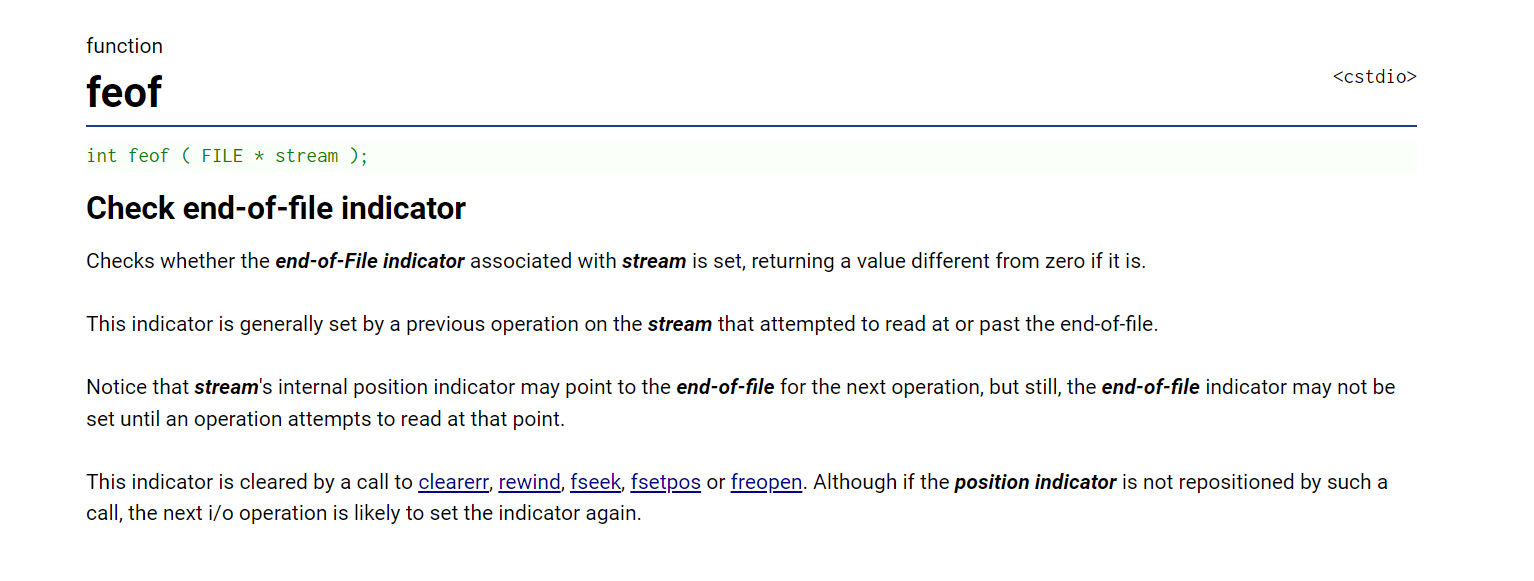
总言 C语言:文件操作。 文章目录总言1、文件是什么?为什么需要文件?1.1、为什么需要文件?1.2、文件是什么?2、文件的打开与关闭2.1、文件指针2.2、文件打开和关闭:fopen、fclose2.3、文件使用方式3、文…...
cmd窗口中java命令报错。错误:找不到或无法加载主类 java的jdk安装过程中踩过的坑
错误: 找不到或无法加载主类 HelloWorld 遇到这个问题时,我尝试过网上其他人的做法。有试过添加classpath,也有试过删除classpath。但是依然报错,这里javac可以编译通过,说明代码应该是没有问题的。只是在运行是出现了错误。我安装…...
)
Breathwork(呼吸练习)
查了下呼吸练习相关内容,做个记录。我又在油管学习啦。 喜欢在you. tube看一些self-help相关的内容。比如学习方法、拉伸、跑步、力量举、自重锻炼等等。 总是听Obi Vicent说起Breathwork,比如: My 6am Morning Routine | New Healthy Habit…...
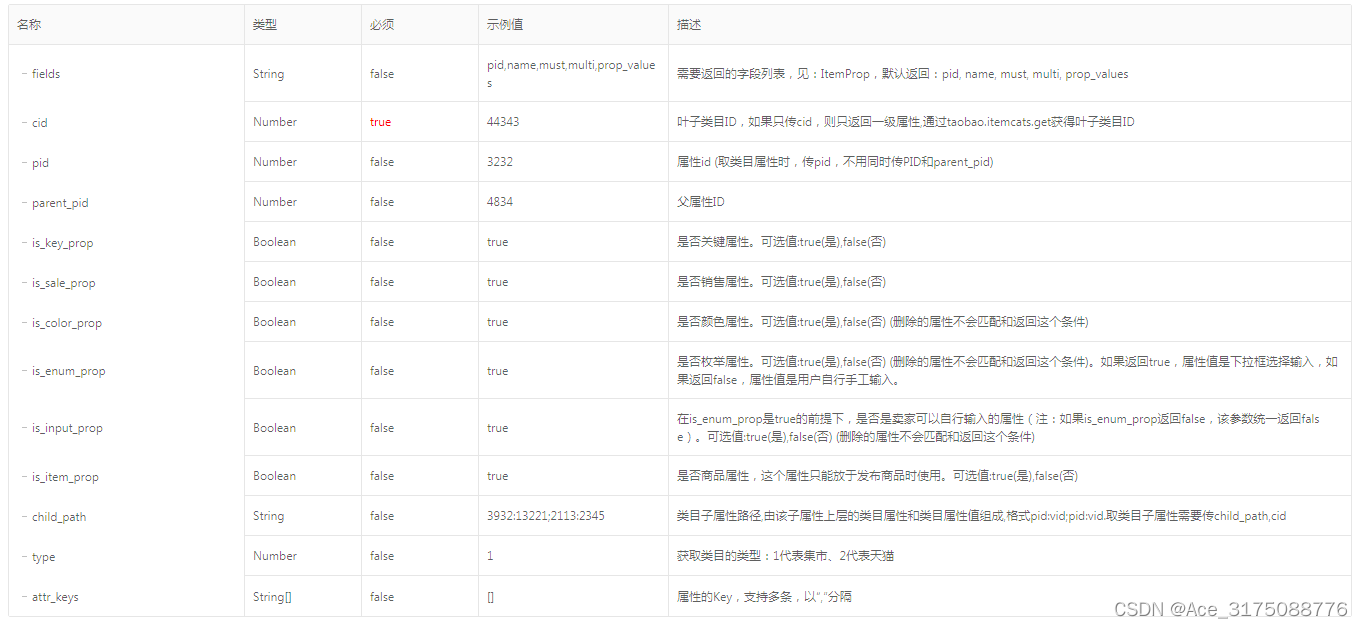
taobao.itemprops.get( 获取标准商品类目属性 )
¥开放平台基础API不需用户授权 通过设置必要的参数,来获取商品后台标准类目属性,以及这些属性里面详细的属性值prop_values。 公共参数 请求地址: HTTP地址 http://gw.api.taobao.com/router/rest 公共请求参数: 公共响应参数: 请求参数 点…...
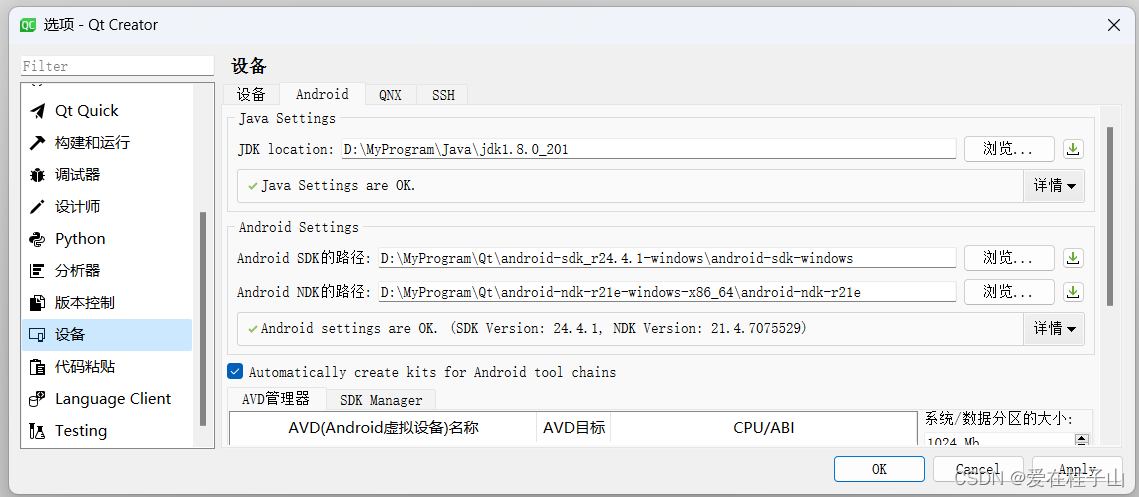
QT配置安卓环境(保姆级教程)
目录 下载环境资源 JDK1.8 NDK SDK 安装QT 配置环境 下载环境资源 JDK1.8 介绍JDK是Java开发的核心工具,为Java开发者提供了一套完整的开发环境,包括开发工具、类库和API等,使得开发者可以高效地编写、测试和运行Java应用程序。 下载…...
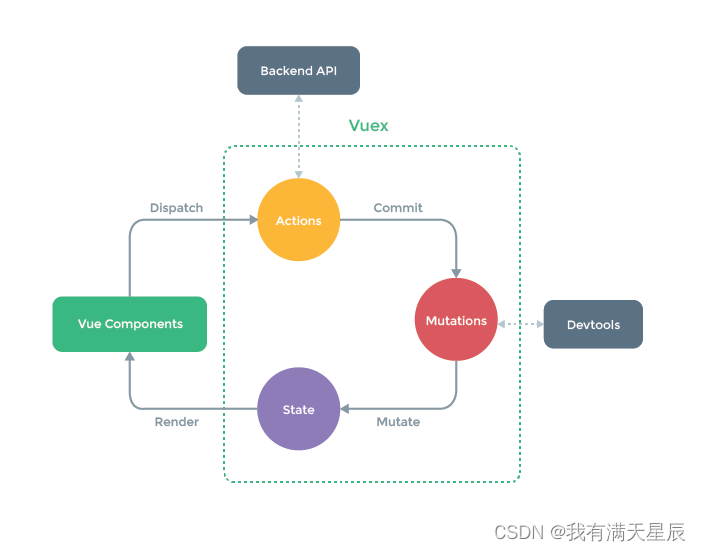
【uni-app教程】八、UniAPP Vuex 状态管理
八、UniAPP Vuex 状态管理 概念 Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式。它采用集中式存储管理应用的所有组件的状态,并以相应的规则保证状态以一种可预测的方式发生变化。 应用场景 Vue多个组件之间需要共享数据或状态。 关键规则 State:…...
)
同花顺测试面经(30min)
大概三十分钟,面试官人还挺好的 1.自我介绍 2.详细问你了自我介绍中的一个实习经历 3.对我们公司有什么了解 !!(高频) 4.对测试有什么看法,为什么选测试 5.黑盒白盒分别是什么 6.对测试左移有什么看法…...

C++-简述#ifdef、#else、#endif和#ifndef的作用
回答如下: #ifdef,#else,#endif和#ifndef都是预处理指令,用于条件编译。#ifdef:这个指令用来判断一个宏是否已经被定义过,如果已经定义过,则执行后面的代码块。#else:这个指令一般与…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
