精品中国货出海wordpress外贸独立站建站模板
旗袍唐装wordpress外贸网站模板
旗袍、唐装、华服wordpress外贸网站模板，适合做衣服生意的外贸公司官网使用。
https://www.jianzhanpress.com/?p=3695
劳动防护wordpress外贸独立站模板
劳动防护wordpress外贸独立站模板，劳动保护、劳动防护用品外贸独立网站模板。
https://www.jianzhanpress.com/?p=3729
数控设备wordpress外贸独立站模板
工业用数制设备wordpress外贸独立站模板，适合做外贸的公司建英文网站使用。
https://www.jianzhanpress.com/?p=3730
仓储设备wordpress外贸独立站模板
仓储、储存、搬运设备wordpress主题，适合做物流仓储企业的wordpress官方网站模板。
https://www.jianzhanpress.com/?p=3721
种子公司wordpress外贸网站模板
农业种子公司wordpress网站模板，适合做农业行业种子公司的企业网站模板。
https://www.jianzhanpress.com/?p=3709
箱包wordpress外贸网站模板
箱包wordpress外贸网站模板，做外贸箱包生产或销售生意的公司官网模板。
https://www.jianzhanpress.com/?p=3716
相关文章：
精品中国货出海wordpress外贸独立站建站模板
旗袍唐装wordpress外贸网站模板 旗袍、唐装、华服wordpress外贸网站模板，适合做衣服生意的外贸公司官网使用。 https://www.jianzhanpress.com/?p3695 劳动防护wordpress外贸独立站模板 劳动防护wordpress外贸独立站模板，劳动保护、劳动防护用品外贸…...
使用Animated.View实现全屏页面可以向下拖动,松开手指页面返回原处的效果
使用Animated.View实现全屏页面可以向下拖动,松开手指页面返回原处的效果 效果示例图代码示例 效果示例图 代码示例 import React, {useRef, useState} from react; import {View,Text,Animated,Easing,PanResponder,StyleSheet, } from react-native;const TestDragCard () …...
【教程】uni-app iOS打包解决profile文件与私钥证书不匹配问题
摘要 当在uni-app中进行iOS打包时，有时会遇到profile文件与私钥证书不匹配的问题。本文将介绍如何解决这一问题，以及相关的技术细节和操作步骤。 引言 在uni-app开发过程中，iOS打包是一个常见的操作。然而，有时会出现profile文…...
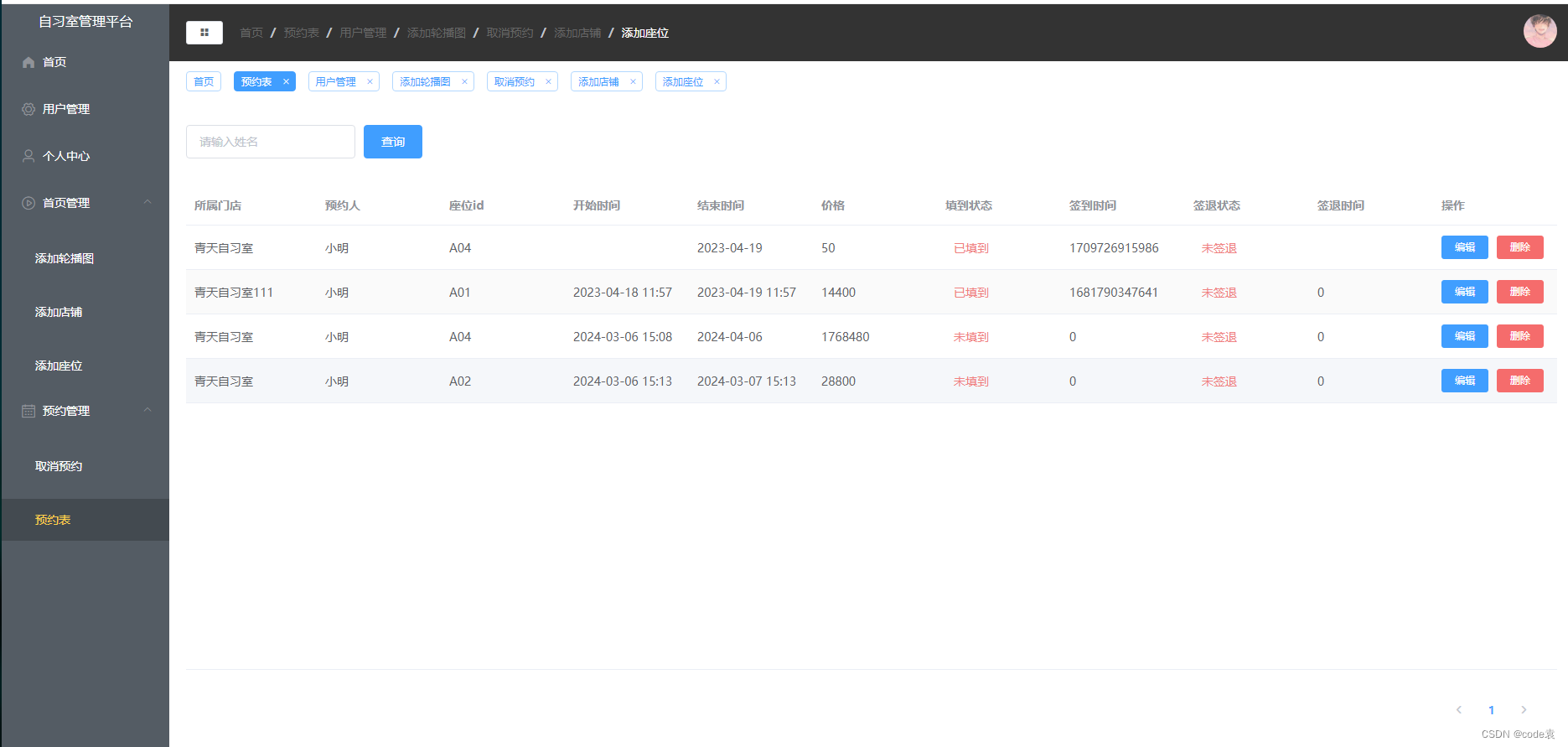
预约自习室
预约自习室 1、技术介绍 自习室预约系统的后端开发语言采用Node，后端开发框架采用Express，数据库采用的Node的最佳搭档MySQL。采用Vue作为前端开发框架，Element-UI作为开发的组件库，微信小程序。期间采用axios实现网页数据获取&a…...
网络安全审计是什么意思？与等保测评有什么区别？
网络安全审计和等保测评在信息安全领域中都是非常重要的环节。但不少人对于这两者是傻傻分不清楚，今天我们就来简单聊聊网络安全审计是什么意思？与等保测评有什么区别？ 网络安全审计是什么意思？ 网络安全审计是通过对网络系统和网…...
HarmonyOS学习——HarmonyOS习题
harmonyOS开发学习课程 HarmonyOS第一课 1.【习题】运行Hello World工程 判断题 1. DevEco Studio是开发HarmonyOS应用的一站式集成开发环境。（√） 2. main_pages.json存放页面page路径配置信息。（√） 单选题 1. 在stage模…...
Python程序怎么让鼠标键盘在后台进行点击，不干扰用户其他鼠标键盘操作
在Python中实现鼠标和键盘在后台点击而不干扰用户的其他操作是一个比较复杂的任务。大多数库，如pyautogui或pynput，都是直接控制鼠标和键盘的，这意味着它们的操作会干扰用户的正常活动。 为了在不干扰用户的情况下实现这一点，你可…...
HTML静态网页成品作业(HTML+CSS)——新年春节介绍网页设计制作(3个页面)
🎉不定期分享源码，关注不丢失哦 文章目录 一、作品介绍二、作品演示1、首页2、子页13、子页2 三、代码目录四、网站代码HTML部分代码CSS部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS，未使用Javacsript代码࿰…...
vue实现base64格式转换为图片
找了很多，但是都不太好用，打算自己总结一个保姆级教学，无需动脑，电脑有电就能实现 在HTML部分，我们需要一个标签来放置图片 <template><div><img :src"imageSrc" alt"未获取到图片&qu…...
【杂言】迟到的 2024 展望
研一下开学已有半月，本来想在家写的新年展望拖到了现在。翻看 2021 年的展望，我发现 flag 基本达成了（除了 12 点睡觉），所以给新的一年立下大方向也是很有必要的。也许等到 60 岁我再回看，也是一件趣事吧。…...
结构体（C语言进阶）（一）
目录 前言 1、结构体声明 1.1 结构体基本概念 1.2 结构体声明 1.3 特殊的结构体声明 1.3.1 匿名结构体声明 1.4 结构体自引用 1.5 结构体变量的定义和初始化 1.6 结构体内存对齐 1.7 修改默认对齐数 1.8 结构体传参 总结 前言 C语言除了有其内置类型，还有…...
【react】对React Router的理解？常用的Router 组件有哪些
1 react-router 是什么 react-router等前端路由的原理大致相同，可以实现无刷新的条件下切换显示不同的页面 路由的本质就是页面的URL发生改变时，页面的显示结果可以根据URL的变化而变化，但是页面不会刷新 因此，可以通过前端路由可…...
生成式 AI
生成式 AI 进入应用爆发期，将极大地推动数字化内容生产与创造。 摘要 生成式 AI （ Generative AI 或 AIGC ） 是利用现有文本、音频文件或图像创建 新内容的技术。过去一年，其技术上的 进展主要来自于三大领域：…...
云计算 3月6号 （crontab-计划任务 日志轮转 免密登录）
一、计划任务 计划任务概念解析 在Linux操作系统中，除了用户即时执行的命令操作以外，还可以配置在指定的时间、指定的日期执行预先计划好的系统管理任务（如定期备份、定期采集监测数据）。RHEL6系统中默认已安装了at、crontab软件…...
Windows Shell命令详解：入门指南
Windows操作系统的Shell命令是执行各种任务和管理系统的关键工具。本文将深入探讨Windows Shell命令的基础知识，介绍常用的命令以及它们的功能和用法，并探讨一些高级技巧，帮助用户更好地利用Shell命令提高工作效率。 1. 什么是Windows Shell命…...
MogDB/openGauss关于PL/SQL匿名块调用测试
MogDB/openGauss 关于 PL/SQL 匿名块调用测试 一、原理介绍 PL/SQL(Procedure Language/Structure Query Language)是标准 SQL 语言添加了过程化功能的一门程序设计语言。 单一的 SQL 语句只能进行数据操作，没有流程控制，无法开发复杂的应用。PL/SQL …...
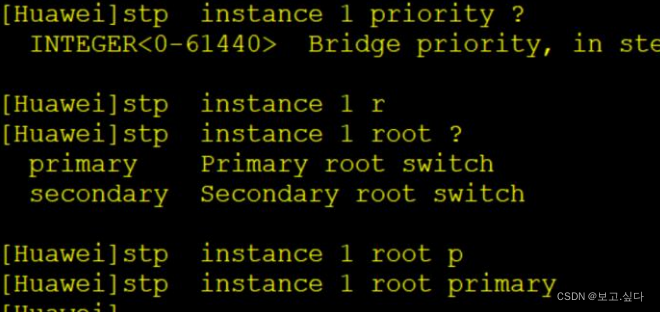
STP---生成树协议
STP的作用 a)Stp通过阻塞端口来消除环路，并能够实现链路备份目的 b)消除了广播风暴 c)物理链路冗余，网络变成了层次化结构的网络 STP操作 选举一个根桥每个非根交换机选举一个根端口每个网段选举一个指定端口阻塞非根，非指定端口 STP--生成树…...
算法D38| 动态规划1 | 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯
理论基础 无论大家之前对动态规划学到什么程度，一定要先看 我讲的 动态规划理论基础。 如果没做过动态规划的题目，看我讲的理论基础，会有感觉 是不是简单题想复杂了？ 其实并没有，我讲的理论基础内容，在动…...
Vue教学13：组件的生命周期：掌握组件的每一个关键时刻
大家好，欢迎回到我们的Vue教学系列博客！在前十二篇博客中，我们学习了Vue.js的基础知识、安装Node.js与npm、使用Vue Devtools进行调试、Vue实例与生命周期钩子、数据绑定（单向与双向）、计算属性与侦听器、条件渲染和列…...
mitmproxy代理
文章目录 mitmproxy1. 网络代理2. 安装3. Https请求3.1 启动mitmproxy3.2 获取证书3.3 配置代理3.4 运行测试 4. 请求4.1 读取请求4.2 修改请求4.3 拦截请求 5. 响应5.1 读取响应5.2 修改响应 6. 案例：共享账号6.1 登录bilibili获取cookies6.2 在代理请求中设置cook…...
【GPU驱动开发】- mesa编译与链接过程详细分析
前言 不必害怕未知，无需恐惧犯错，做一个Creator！ 一、总体框架图 暂时无法在飞书文档外展示此内容 二、Mesa API 处理 OpenGL 函数调用 Mesa API 负责实现 OpenGL 和其他图形 API 的函数接口。Mesa API 表是一个重要的数据结构…...
如何恢复已删除的华为手机图片？5 种方式分享
不幸的现实是，华为的珍贵时刻有时会因为意外删除、软件故障或其他不可预见的情况而在眨眼之间消失。在这种情况下，寻求恢复已删除的图片成为个人迫切关心的问题。 本文旨在为用户提供如何从华为恢复已删除图片的实用解决方案。我们将探索五种可行的方法…...
通过 python 和 wget 批量下载文件（在Linux/Ubuntu/Debian中测试）
首先创建一个文本文件d.txt, 一行一个链接。 你可以使用简单的 Python 脚本逐行读取文件 (d.txt) 中的链接，并使用 wget 下载文件： import subprocess# File containing download links (replace with your file path) file_path d.txt# Function to …...
个人博客系列-后端项目-RBAC角色管理（6）
设计用户表 ## 用户表 class User(models.Model):username models.CharField(max_length255, uniqueTrue, verbose_name"手机号")password models.CharField(max_length255, uniqueFalse, verbose_name"密码")is_vip models.BooleanField(defaultFalse…...
机器学习-启航
文章目录 原理分析机器学习的两种典型任务机器学习分类总结数据机器学习分类解读简单复杂 原理分析 马克思主义哲学-规律篇 规律客观存在，万事万物皆有规律。 机器学习则是多维角度拆解分析复杂事实数据，发现复杂事实背后的规律，然后将规律用…...
驱动调试第014期-变频调速的原理及相关计算公式应用
一、引言 变频调速是一种通过改变电源频率来实现电动机调速的技术。它具有高效、精确、可靠等优点，广泛应用于工业、商业和家用领域。本文将介绍变频调速的基本原理、优点以及应用领域，并通过详细的公式计算过程和图片说明来帮助读者更好地理解。 二、变…...
JavaWeb环境配置 IDE2022版
一、新建一个javaweb文件 文件名可以自己随意改 二、给建立的项目添加框架支持 勾选Web Application,点击确定 建立成功界面，会生成一个新的web文件夹 三、配置tomcat 1、两种打开配置文件方式： 第一种 第二种 2、打开后，点击号…...
Matlab偏微分方程拟合 | 完整源码 | 视频教程
专栏导读 作者简介：工学博士，高级工程师，专注于工业软件算法研究本文已收录于专栏：《复杂函数拟合案例分享》本专栏旨在提供 1.以案例的形式讲解各类复杂函数拟合的程序实现方法，并提供所有案例完整源码；2.…...
什么是yocto基本组件（bitbake,recipes,classes,configuration,layer)
文章目录 1基本组件1.1 bitbake1.2 Recipes1.3 Classes1.4 Configurations2 层的理解2.1 层结构2.2 nxp yocto示例2.3 ti yocto示例1基本组件 1.1 bitbake bitbake，是OpenEmbedded构建系统的核心工具，负责解析元数据，从中生成任务列表，然后执行这些任务。bitbake是一个通…...
electron 程序与安装包图标放大与制作
原因 electron-builder 在打包时需要最小支持到256x256像素的icon图标。原有历史图标都太小了。需要尝试将图标放大。 工具 convertio.co/zh/ico-png/ 在线ico转png网站 https://github.com/upscayl/upscayl 图片放大工具 csdn下载 greenfish-icon-editor-pro.en.softonic.c…...