第十四届蓝桥杯蜗牛
蜗牛 线性dp
目录
蜗牛 线性dp
先求到达竹竿底部的状态转移方程
求蜗牛到达第i根竹竿的传送门入口的最短时间编辑
题目链接:蓝桥杯2023年第十四届省赛真题-蜗牛 - C语言网
关键在于建立数组将竹竿上的每个状态量表示出来,并分析出状态转移方程
int tree [] = new int[n];//记录每根竹竿到原点的距离int portal_exit [] = new int[n];//第i个竹竿上传送门出口高度int portal_entrance [] = new int[n];//第i个竹竿上传送门入口的高度double time_bottom [] = new double[n];//到达第i个竹竿底部的最短时间double time_portal [] = new double[n];//到达第i个竹竿传送门入口的最短时间注意:到达第i个竹竿传送门入口的最短时间也是,蜗牛传送到第i+1根竹竿传送门出口的最短时间
很明显,代码中表示最状态的数组为 time_bottom[i]表示蜗牛从原点到达第i根竹竿的底部用的最短时间
time_portal[i] 表示蜗牛从原点到达第i根竹竿可以传送到第i+1竹竿的传送门入口 a1的最短1时间
我们需要求出time_bottom[i]和time_poratal[i]的状态转移方程
先求到达竹竿底部的状态转移方程
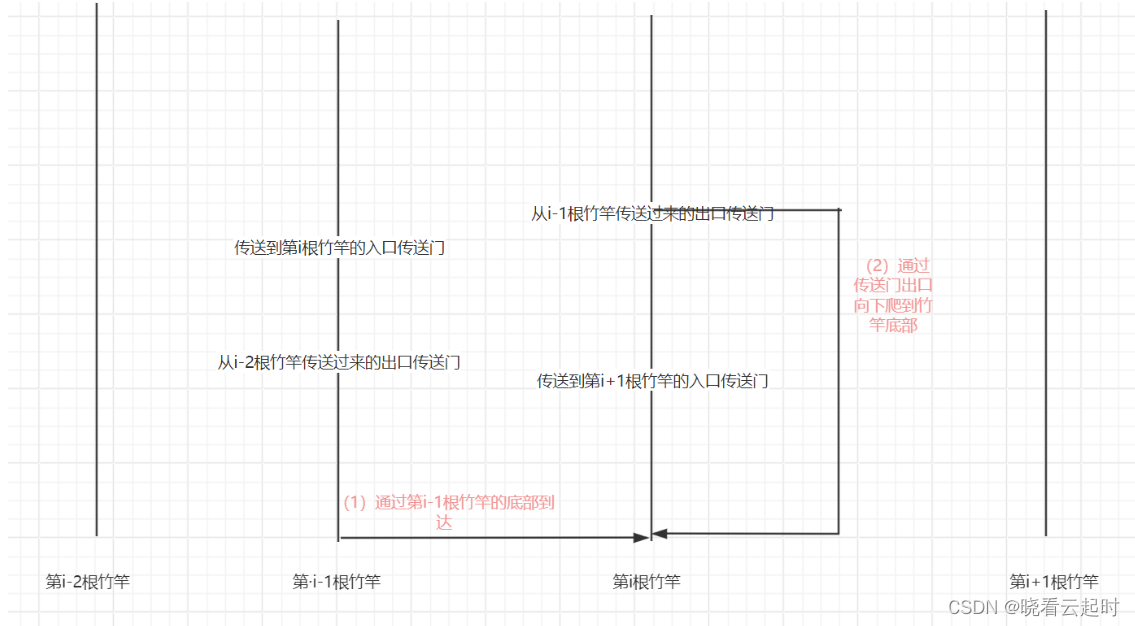
由图可知
到达第i竹竿底部的方法有两种
(1)从前一个竹竿的底部直接爬过来
time_bottom[i]=time_bottom[i-1]+tree[i]-tree[i-1];ps:tree[i]-tree[i-1]为蜗牛从前一个竹竿爬过来用的时间
(2)从当前竹竿的传送门出口爬下来
到达第i根竹竿底部的时间=蜗牛到达第i根竹竿的传送门出口的时间(即到达第i-1竹竿传送门入口的时间:time_portal[i-1])+ 传送门出口到底部距离/下爬速度
time_bottom[i]=time_portal[i-1]+portal_exit[i]/1.3;
综合(1)(2)得time_bottom[i]得状态转移方程
time_bottom[i]=Math.min(time_bottom[i-1]+tree[i]-tree[i-1],time_portal[i-1]+portal_exit[i]/1.3)求蜗牛到达第i根竹竿的传送门入口的最短时间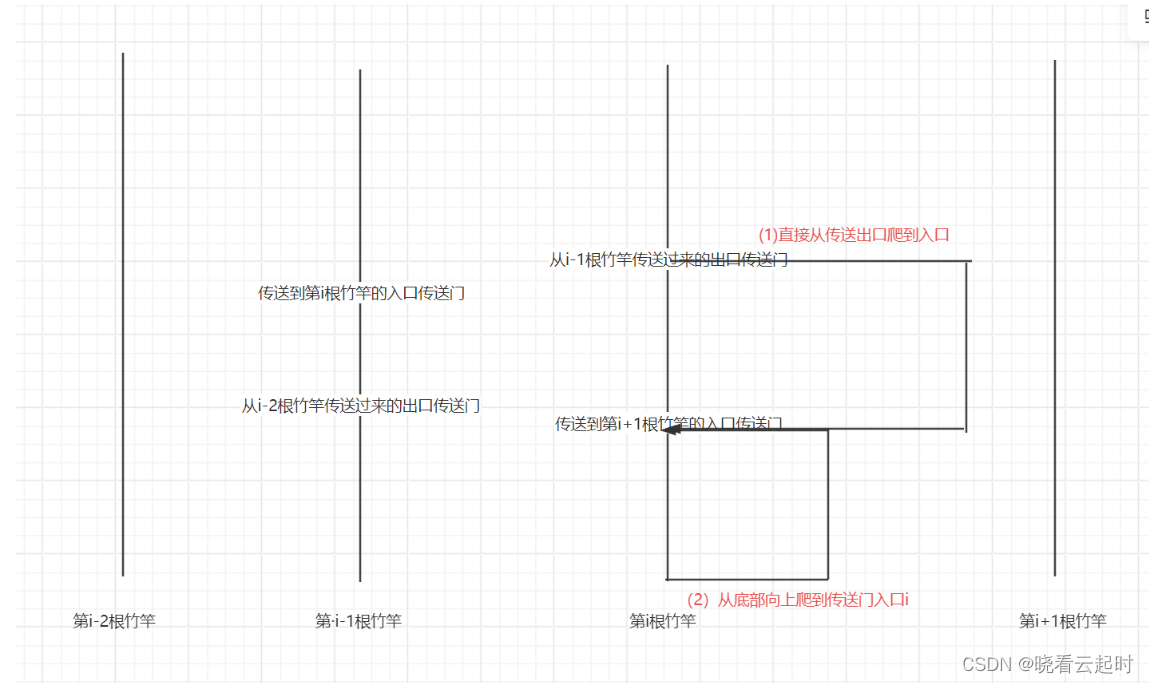
同样有两种方式
(1)从传送门出口爬到传送门入口
如果传送门出口比传送门入口高那么直接向下爬
到达传送门出口的时间+传送门出口-传送门入口的距离/速度
time_portal[i]=time_protal[i-1]+(portal_exit[i]-portal_entrance[i])/1.3;如果传送门出口的高度比入口的低那么就要向上1爬速度为0.7
(2)从底部爬到传送门
time_portal[i]=time_bottom[i]+portal_entrance[i]/0.7;综上time_portal[i]的状态转移方程为:(传送门出口比传送门入口高的情况)
ime_portal[i]=Math.min(time_protal[i-1]+(portal_exit[i]-portal_entrance[i])/1.3,time_bottom[i]+portal_entrance[i]/0.7)最后我们可以给第1根竹竿的状态初始化
//第一根竹竿的底部和传送出口最短时间我们可以算出来
time_bottom[0]=tree[0];//1time_portal[0]=tree[0]+portal_entrance[0】;第n根竹竿我们要特殊判断一下因为最后一根竹竿没有传送门入口
完整代码
import java.util.Scanner;public class Snail {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int tree [] = new int[n];//记录每根竹竿到原点的距离int portal_exit [] = new int[n];//第i个竹竿上传送门出口高度int portal_entrance [] = new int[n];//第i个竹竿上传送门入口的高度double time_bottom [] = new double[n];//到达第i个竹竿底部的最短时间double time_portal [] = new double[n];//到达第i个竹竿传送门入口的最短时间for (int i=0;i<n;i++){tree[i]=sc.nextInt();}for (int i=0;i<n-1;i++){portal_entrance[i]=sc.nextInt();portal_exit[i+1]=sc.nextInt();}
//第一根竹竿的底部和传送出口最短时间我们可以算出来time_bottom[0]=tree[0];//1time_portal[0]=tree[0]+portal_entrance[0]/0.7;//2.4for (int i=1;i<n;i++){
// 给出结束条件if (i==n-1){
// 从上一根竹竿底部直接到第i根竹竿底部double bottom1 = time_bottom[i-1]+tree[i]-tree[i-1];
// 从第i根竹竿的传送门出口向下爬到底部double bottom2 = time_portal[i-1]+portal_exit[i]/1.3;time_bottom[i]=Math.min(bottom1,bottom2);break;}else{// 从上一根竹竿底部直接到第i根竹竿底部double bottom1 = time_bottom[i-1]+tree[i]-tree[i-1];
// 从第i根竹竿的传送门出口向下爬到底部double bottom2 = time_portal[i-1]+portal_exit[i]/1.3;//3.2
// 计算最短到达第i根竹竿底部的距离time_bottom[i]=Math.min(bottom1,bottom2);//3.2
// 计算到达第i根竹竿传送门入口的最短时间
// 到达传送门入口的第一种方式:从底部爬到入口double time_entrance1=time_bottom[i]+portal_entrance[i]/0.7;
// 到达传送门入口的第二种方式:从传送门的出口爬到入口double time_entrance2=0;if (portal_entrance[i]>=portal_exit[i]){//如果入口在出口上面,向上爬time_entrance2=time_portal[i-1]+(portal_entrance[i]-portal_exit[i])/0.7;}else {time_entrance2=time_portal[i-1]+(portal_exit[i]-portal_entrance[i])/1.3;}
// 从两种方式中取最短时间time_portal[i]=Math.min(time_entrance1,time_entrance2);}}System.out.printf("%.2f",time_bottom[n-1]);}
}写下血与泪的教训:时间的数据类型一定要用double不然数据量太大精度不够不能通过。
相关文章:

第十四届蓝桥杯蜗牛
蜗牛 线性dp 目录 蜗牛 线性dp 先求到达竹竿底部的状态转移方程 求蜗牛到达第i根竹竿的传送门入口的最短时间编辑 题目链接:蓝桥杯2023年第十四届省赛真题-蜗牛 - C语言网 关键在于建立数组将竹竿上的每个状态量表示出来,并分析出状态转移方程 in…...
分布式定时任务调度xxl-job
1. xxl-job基本介绍 1.1 Quartz的体系结构 Quartz中最重要的三个对象:Job(作业)、Trigger(触发器)、Scheduler(调度器)。 xxl-job的调度原理:调度线程在一个while循环中不断地获取一定数量的即将触发的Tr…...

自动化运维利器Ansible基础(环境部署)
Ansible 介绍及安装 1. 介绍 Ansible 是⼀个 IT ⾃动化⼯具。它能配置系统、部署软件、编 排更复杂的 IT 任务,如连续部署或零停机时间滚动更新。 Ansible ⽤ Python 编写,尽管市⾯上已经有很多可供选择的 配置管理解决⽅案(例如 Salt、Pupp…...
微服务自动化管理初步认识与使用
目录 一、ETCD 1.1、ETCD简介 对于实施工程师: 1.2、特点 1.3. 使用场景 1.4、 关键字 1.5 工作原理 二、ETCD的安装 2.1、下载路径 2.2、介绍 2.3、具体操作 安装服务端 安装etcd客户端 测试 三、ETCD使用 3.1、前奏具体操作 3.2、 常用操作 一、ET…...

使用Docker管理linux容器
文章目录 一、使用docker管理镜像 二、使用docker管理容器 一、使用docker管理镜像 1、安装操作系统,我安装的是centOS 7 ,因为centos7有着非常丰富的软件仓库,方便后续安装与docker相关的软件。 2、初始化设置, 关闭防火墙 关闭…...
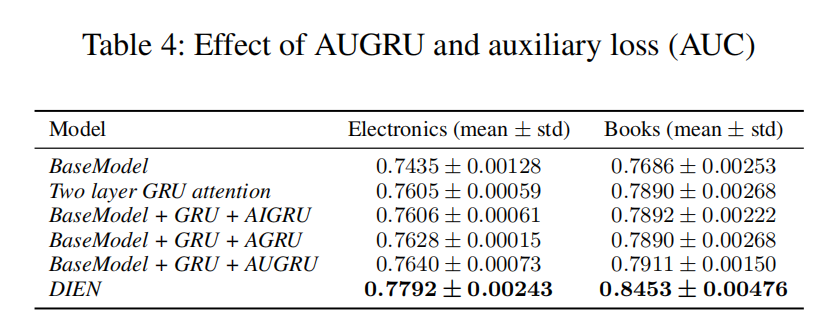
CTR之行为序列建模用户兴趣:DIEN
前言 在上一篇文章中 CTR之行为序列建模用户兴趣:DIN,开启了用户行为序列建模用户兴趣的篇章。DIN引入了Attention机制,对于不同的候选item,可以根据用户的历史行为序列,动态地学习用户的兴趣表征向量。但是ÿ…...
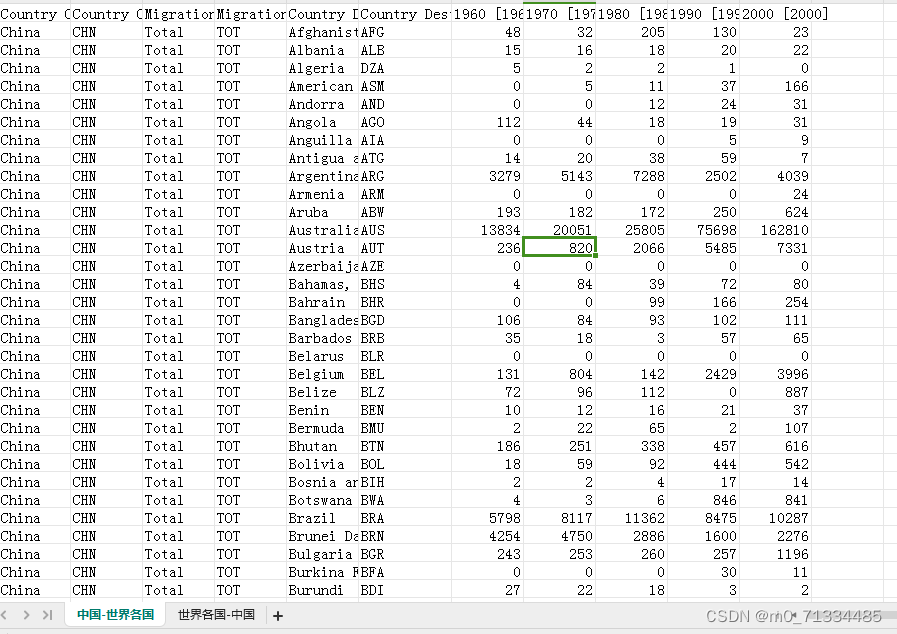
1960-2020年全球双边迁移数据库(Global Bilateral MigrationDatabase)
1960-2020年全球双边迁移数据库(Global Bilateral MigrationDatabase) 1、时间:1960-2000年,每10年一次具体为:1960年、1970年、1980年、1990年、2000年 2、来源:世界银行 3、指标:Country O…...

OpenGL-贴纸方案
OpenGL-贴纸方案 普通贴纸(缩放、Z轴旋转、平移) OpenGL环境说明 OpenGL渲染区域使用正交投影换算,正常OpenGL坐标是vertexData,这样的 Matrix.orthoM 进行换算 //顶点坐标(原点为显示区域中心店)private final float[] vertex…...
【性能测试】移动测试md知识总结第1篇:移动端测试课程介绍【附代码文档】
移动测试完整教程(附代码资料)主要内容讲述:移动端测试课程介绍,移动端测试知识概览,移动端测试环境搭建,ADB常用命令学习主要内容,学习目标,学习目标,1. window安装andorid模拟器,学习目标。主流移动端自动…...
)
Vue2和vue3的区别(前端面试常见问题)
1.Api的变化:vue3使用组合式Api(compostion Api)和Vue2是选项式Api(options Api)。选项式Api具有data ,watch,methods,computed,一个个的模块。如果代码过多可读性会很差…...

openGauss学习笔记-241 openGauss性能调优-SQL调优-审视和修改表定义
文章目录 openGauss学习笔记-241 openGauss性能调优-SQL调优-审视和修改表定义241.1 审视和修改表定义概述241.2 选择存储模型241.3 使用局部聚簇241.4 使用分区表241.5 选择数据类型 openGauss学习笔记-241 openGauss性能调优-SQL调优-审视和修改表定义 241.1 审视和修改表定…...
)
PDFPlumber解析PDF文本报错:AssertionError: (‘Unhandled’, 6)
文章目录 1、问题描述2、问题原因3、问题解决 1、问题描述 今天在使用PDFPlumber模块提取PDF文本时extract_text()方法报错,报错内容如下: Traceback (most recent call last):......File "F:\Python\...\site-packages\pdfminer\pdffont.py"…...

51WORLD正式落地中东,助力沙特伙伴与客户数字化升级!
近日,在被誉为中东“数字达沃斯”的LEAP科技展上,51WORLD首次震撼亮相Digital Twin Riyadh2924k㎡ 全要素城市底座、数字地球平台51Earth,向中东及全球科技从业者展现中国企业技术实力与创新能力。此外,以LEAP为起点,5…...
嵌入式学习38-数据库
数据库软件: 关系型数据库: Mysql (开源) Oracle SqlServer Sqlite (小型数据) 非关系型数据库:(快速查找数据) Redis NoSQ…...

去除PDF论文行号的完美解决方案
去除PDF论文行号的完美解决方案 1. 遇到的问题 我想去除论文的行号,但是使用网上的Adobe Acrobat裁剪保存后 如何去掉pdf的行编号? - 知乎 (zhihu.com) 翻译时依然会出现行号,或者是转成word,这样就大大损失了格式,…...
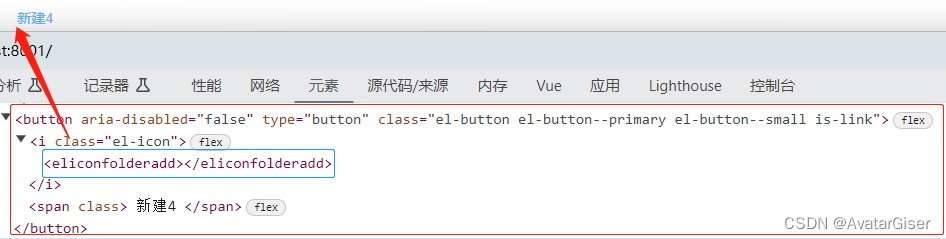
《ElementPlus 与 ElementUI 差异集合》icon 图标使用(包含:el-button,el-input和el-dropdown 差异对比)
安装 注意 ElementPlus 的 Icon 图标 要额外安装插件 element-plus/icons-vue. npm install element-plus/icons-vue注册 全局注册 定义一个文件 element-icon.js ,注意代码第 6 行。加上了前缀 ElIcon ,避免组件命名重复,且易于理解为 e…...

力扣题库第8题:去重后的最长子串
题目: 给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。 示例 2: 输入: s "bbbbb" …...

CSS样式中长度单位含义解析:rpx、px、vw、vh、em、rem、pt
在 CSS 样式中,有几种常见的长度单位,包括 rpx 、 px 、 vw 和 vh 等,含义解析如下: 1 . rpx (响应像素): 是微信小程序中的一种相对长度单位,可以根据屏幕宽度进行自适应缩放。 1rp…...
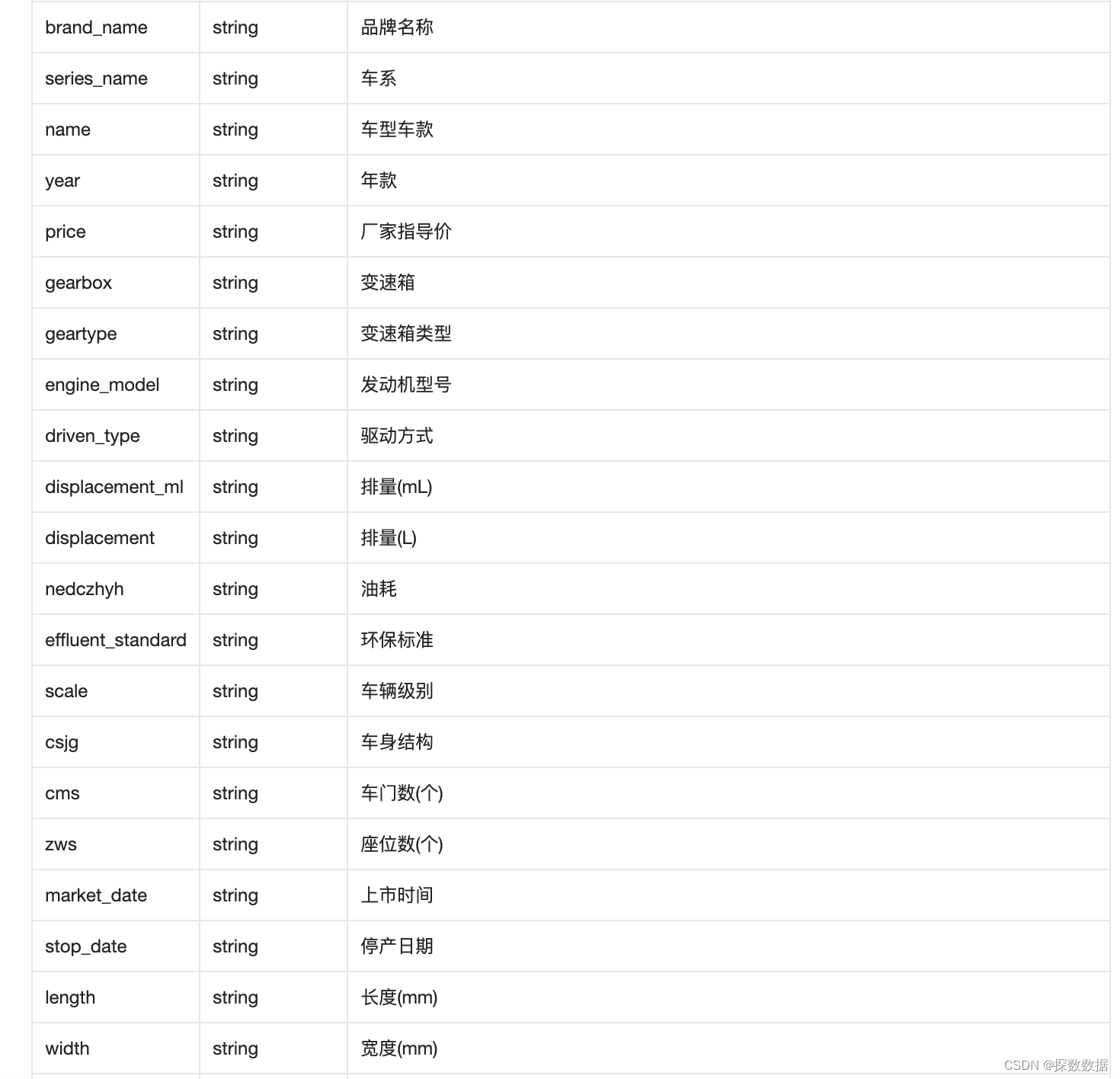
全国车辆识别代码信息API查询接口-VIN深度解析
我们先来介绍下什么是vin码,以及vin码的构成结构解析,汽车VIN码,也叫车辆识别号码,通俗可以理解为汽车的身份证号码。 VIN码一共分四大部分: 1~3位,是世界制造厂识别代号(WMI)&…...

python django 模型中字段设置blank, null属性值用法说明
问题1: ShareUser models.CharField(max_length128, blankTrue) blank设置True和false分别代表什么含义, 有什么区别?chatgpt回答的答案如下: 在 Django 模型字段中,blank 参数用于指定在创建对象时该字段是否可以为空值。它的含义如下: blankTrue:…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
