Chapter 13 Techniques of Design-Oriented Analysis: The Feedback Theorem
Chapter 13 Techniques of Design-Oriented Analysis: The Feedback Theorem
从这一章开始讲负反馈Control系统和小信号建模.
13.2 The Feedback Theorem
首先介绍 Middlebrook’s Feedback Theorem
考虑下面负反馈系统
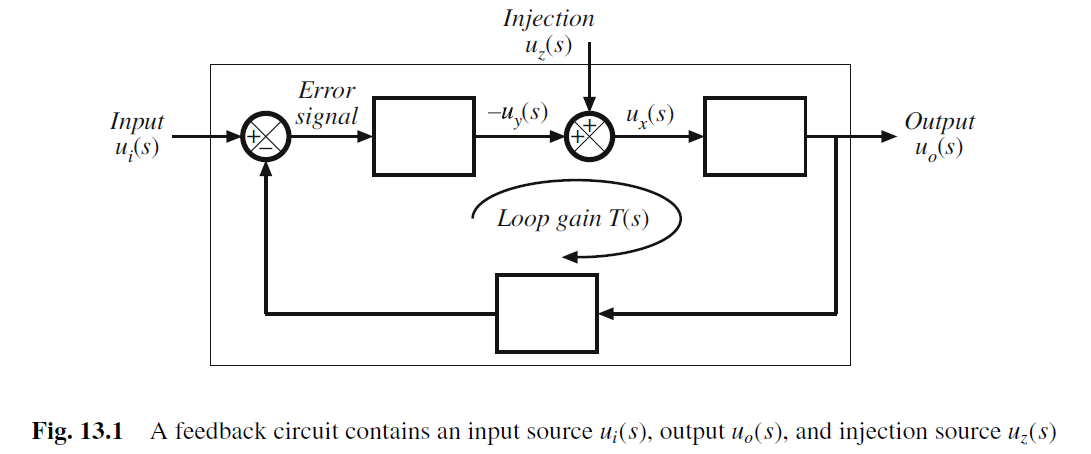
传输函数 G=uo/ui
G ( s ) = u o u i = G ∞ T 1 + T + G 0 1 1 + T G(s)=\frac{u_{o}}{u_{i}}=G_{\infty }\frac{T}{1+T}+G_{0}\frac{1}{1+T} G(s)=uiuo=G∞1+TT+G01+T1
T为Loop Gain 环路的增益
T ( s ) = u y ( s ) u x ( s ) ∣ u i = 0 T(s)=\frac{u_{y}(s)}{u_{x}(s)}\bigg|_{ui=0} T(s)=ux(s)uy(s) ui=0
ideal forward gain 理想正向增益, G_inf为通过uz 消除(null) uy后, ui到uo的传输函数.
G_inf其实就是利用运放虚短和虚断来推导Vout/Vin
G ∞ ( s ) = u o ( s ) u i ( s ) ∣ u y → 0 G_{\infty }(s)=\frac{u_{o}(s)}{u_{i}(s)}\bigg|_{u_y\to 0} G∞(s)=ui(s)uo(s) uy→0
当Loop Gain T-> inf时, G=G_inf
G0为通过uz 消除(null) ux后, ui到uo的传输函数
G 0 ( s ) = u o ( s ) u i ( s ) ∣ u x → 0 G_{0}(s)=\frac{u_{o}(s)}{u_{i}(s)}\bigg|_{u_x\to 0} G0(s)=ui(s)uo(s) ux→0
当Loop Gain T-> 0时, G=G0
Null loop Gain Tn(s): 引入Uz来消除null uo(s)
T n ( s ) = u y ( s ) u x ( s ) ∣ u 0 → 0 T_n(s)=\frac{u_{y}(s)}{u_{x}(s)}\bigg|_{u_0\to 0} Tn(s)=ux(s)uy(s) u0→0
T n ( s ) T ( s ) = G ∞ ( s ) G 0 ( s ) \frac{T_n (s)}{T(s)}=\frac{G_\infty (s)}{G_0(s)} T(s)Tn(s)=G0(s)G∞(s)
13.3 Example: Op Amp PD Compensator Circuit
我们以下面负反馈op-amp为例

假设运放为单极点系统
G o p ( s ) = G o p 0 ( 1 + s ω 1 ) G_{op}(s)=\frac{G_{op0}}{(1+\frac{s}{\omega_1})} Gop(s)=(1+ω1s)Gop0
Voltage injection模型为
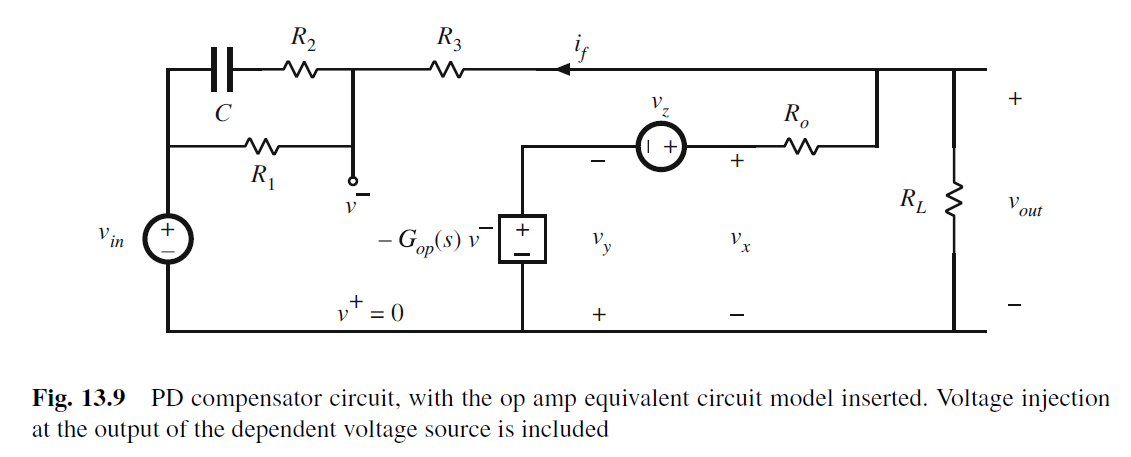
Ideal forward gain: 其实就是利用运放虚短和虚断来推导Vout/Vin, 即G_inf
G ∞ ( s ) = v o u t ( s ) v i n ( s ) ∣ v y → 0 G_{\infty }(s)=\frac{v_{out}(s)}{v_{in}(s)}\bigg|_{v_y\to 0} G∞(s)=vin(s)vout(s) vy→0
vy null to 0, 因此op输入端v-也被null to 0.
我们可以用运放的虚短和虚断特性来推导vout/vin. v- = v+ = 0即virtual ground

Loop Gain, T(s) 环路的增益.
T ( s ) = v o u t v x v − v o u t v y v − T(s)=\frac{v_{out}}{v_{x}}\frac{v{^-}}{v_{out}}\frac{v_y}{v{^-}} T(s)=vxvoutvoutv−v−vy
前两项就是电阻电容的voltage divider传输函数, 第三项为Gop
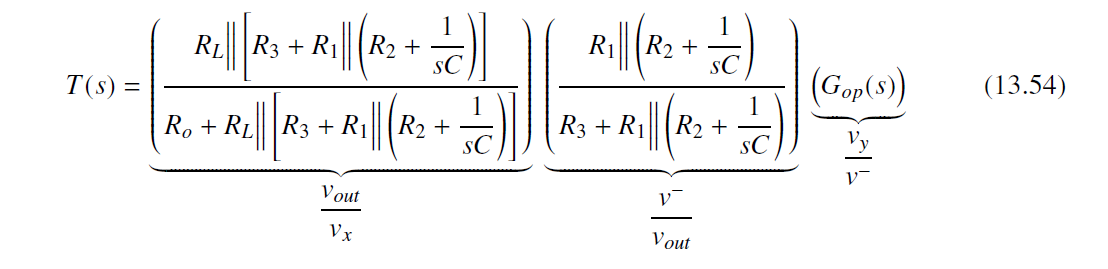
G0为调节Vz, 从而Vx nulled to 0. 即运放输出为0
G 0 ( s ) = v o u t ( s ) v i n ( s ) ∣ v x → 0 G_{0}(s)=\frac{v_{out}(s)}{v_{in}(s)}\bigg|_{v_x\to 0} G0(s)=vin(s)vout(s) vx→0
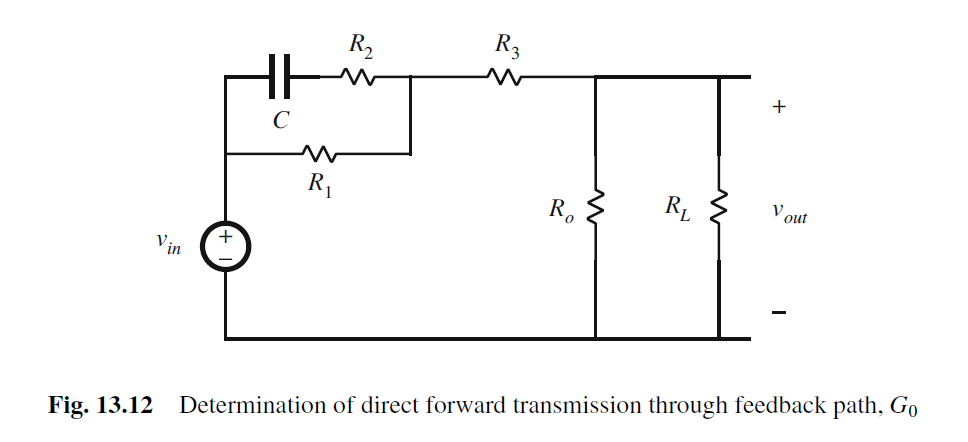
因此G0也是电阻电容的voltage divider传输函数

Tn为null output的loop gain
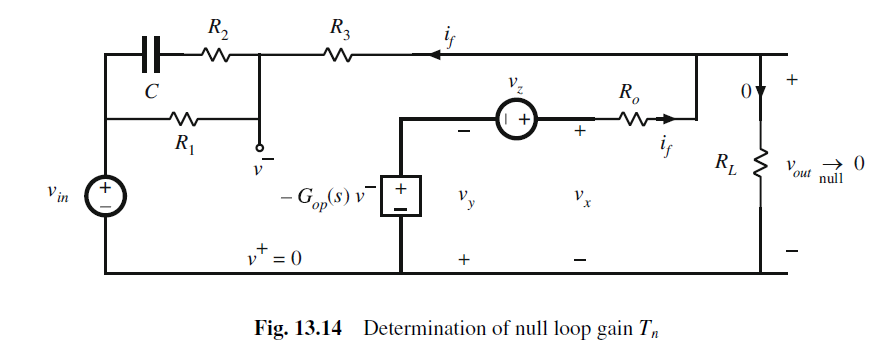
T n ( s ) = v y ( s ) v x ( s ) ∣ v o u t → 0 T_{n }(s)=\frac{v_{y}(s)}{v_{x}(s)}\bigg|_{v_{out}\to 0} Tn(s)=vx(s)vy(s) vout→0
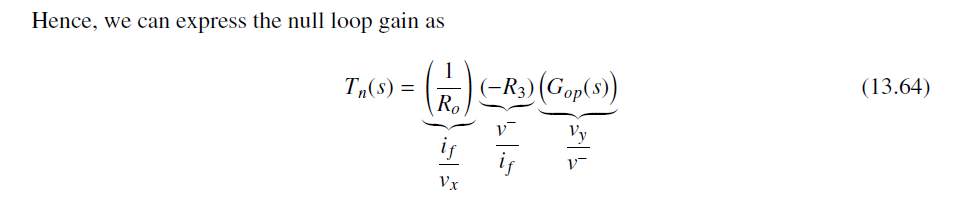
因此Loop Gain可推导为
T ( s ) = G 0 ( s ) T n ( s ) G ∞ ( s ) T(s)=\frac{G_{0}(s)T_{n}(s)}{G_{\infty }(s)} T(s)=G∞(s)G0(s)Tn(s)
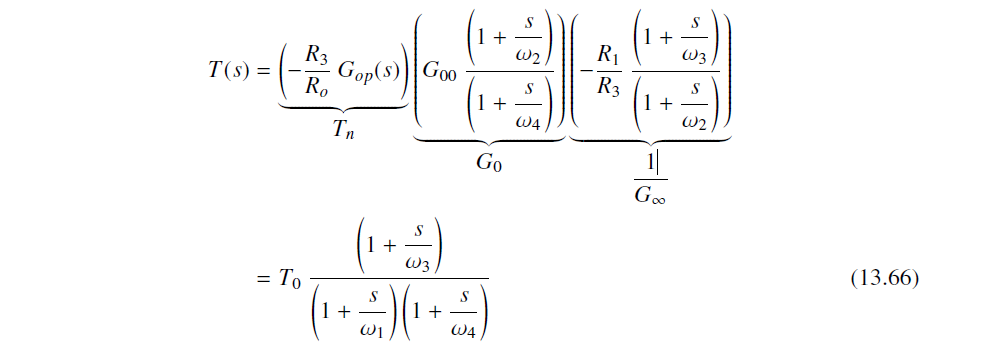
最终Transfer Function, G= Vout/Vin
G ( s ) = v o u t v i n = G ∞ T 1 + T + G 0 1 1 + T G(s)=\frac{v_{out}}{v_{in}}=G_{\infty }\frac{T}{1+T}+G_{0}\frac{1}{1+T} G(s)=vinvout=G∞1+TT+G01+T1

f<30MHz, G0/(1+T)很小,
当f<fc (crossover frequency),G = G_inf
当f>fc (crossover frequency), G和G_inf差异很大
13.4 Example: Closed-Loop Regulator
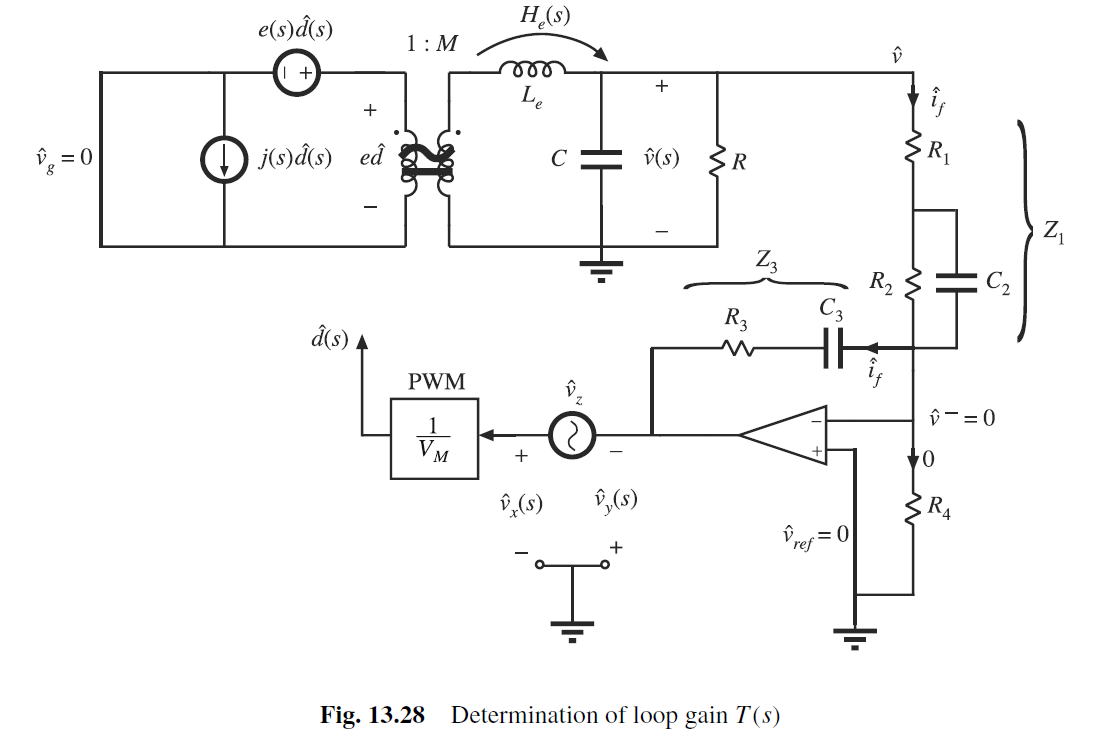
Chapter 14 Circuit Averaging, Averaged Switch Modeling, and Simulation
这一章讲电路的平均化 Circuit averaging.
其核心思想就是把switch+diode替换成理想开关, 然后加上小信号模型
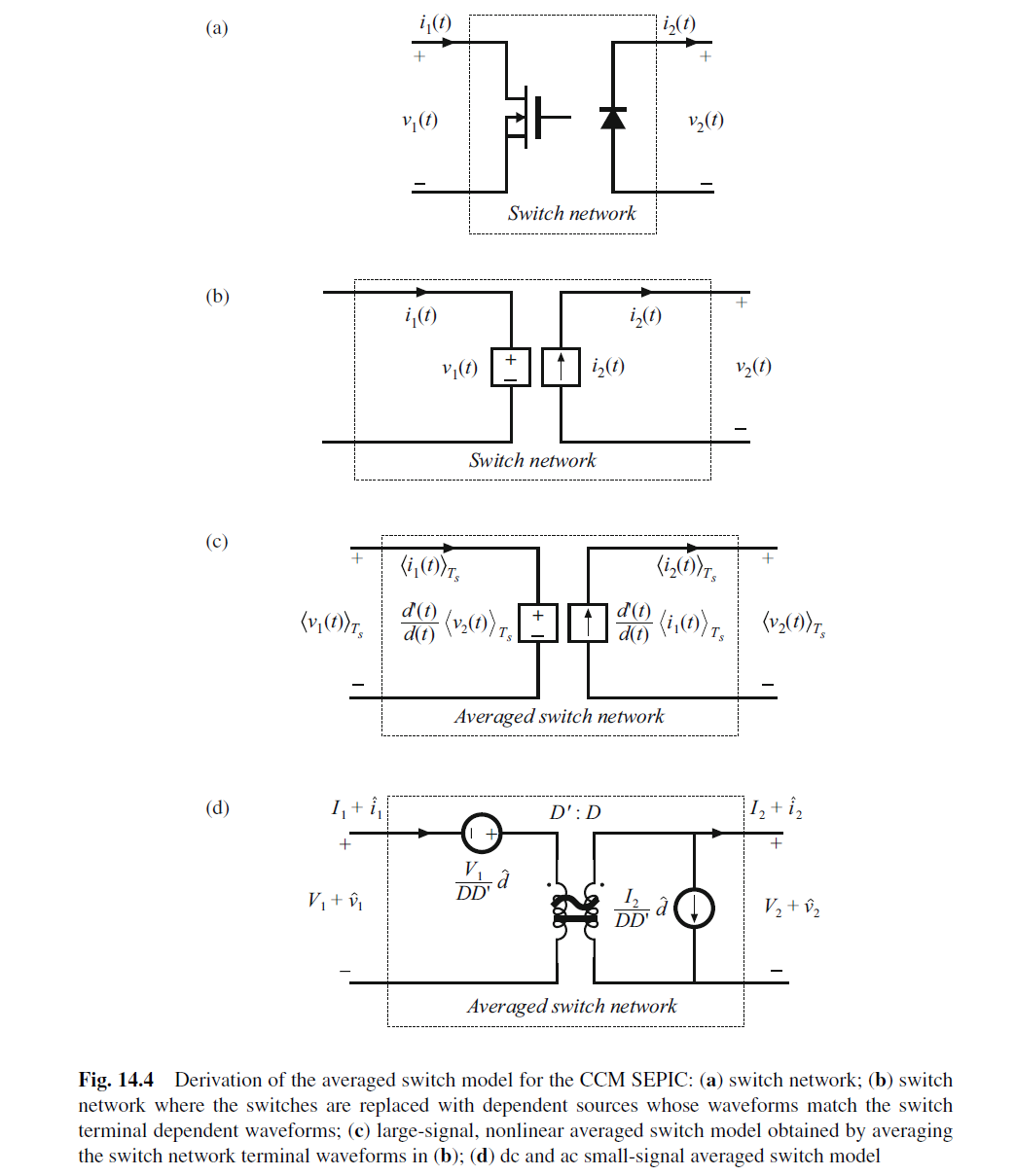
buck, boost, general two-switch的小信号模型如下
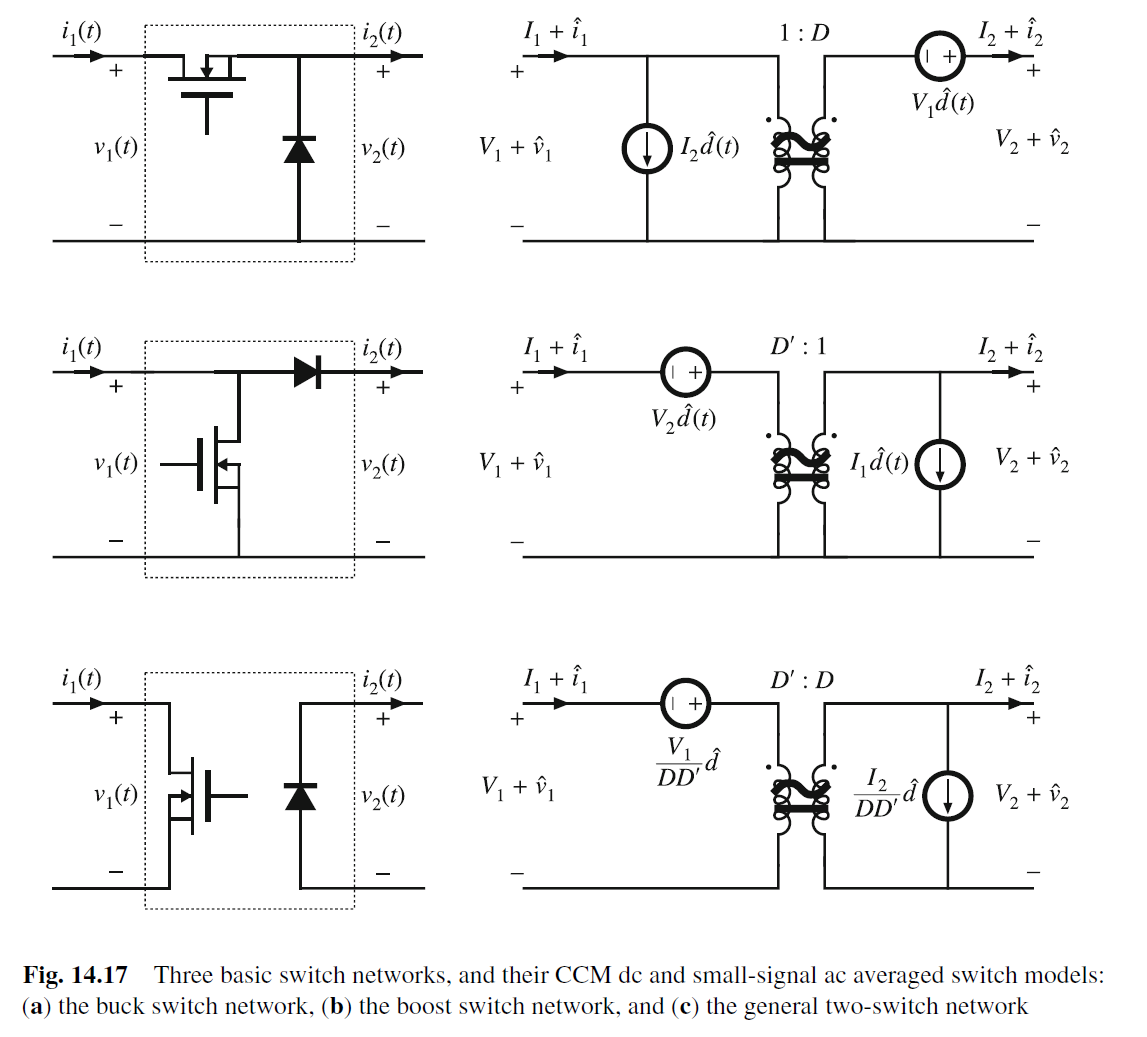
这样就能推导出converter的小信号模型了
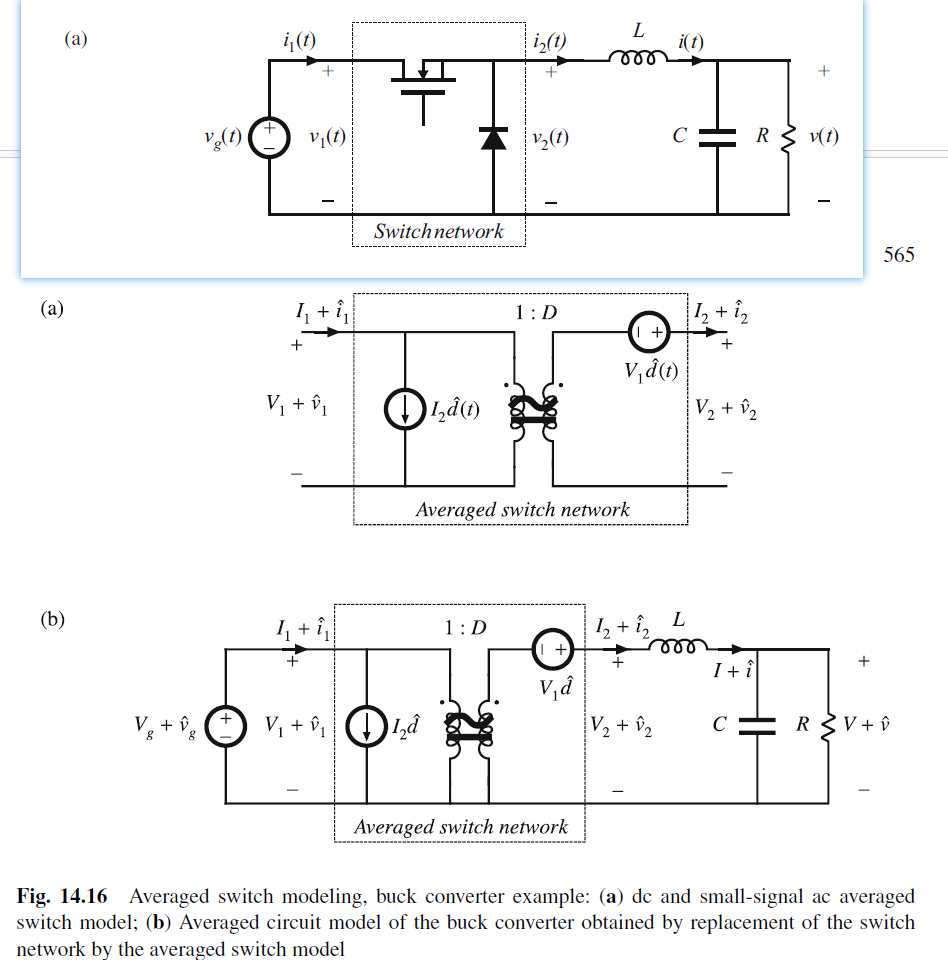
对于电力电子系统的设计和仿真, 分为三种:
- 利用自带的器件库, 采用Cadence, SPICE, LTSpice等工具进行transient仿真. 好处精度高, 坏处费时费力.
- 简化器件模型, MOS换成Ron, 用PLECS and SIMPLIS仿真
- 平均化模型. 研究steady-state下电压,电流波形, 忽略ripple. 研究小信号模型. 可以给设计insight提供指导.
相关文章:

Chapter 13 Techniques of Design-Oriented Analysis: The Feedback Theorem
Chapter 13 Techniques of Design-Oriented Analysis: The Feedback Theorem 从这一章开始讲负反馈Control系统和小信号建模. 13.2 The Feedback Theorem 首先介绍 Middlebrook’s Feedback Theorem 考虑下面负反馈系统 传输函数 Guo/ui G ( s ) u o u i G ∞ T 1 T G…...
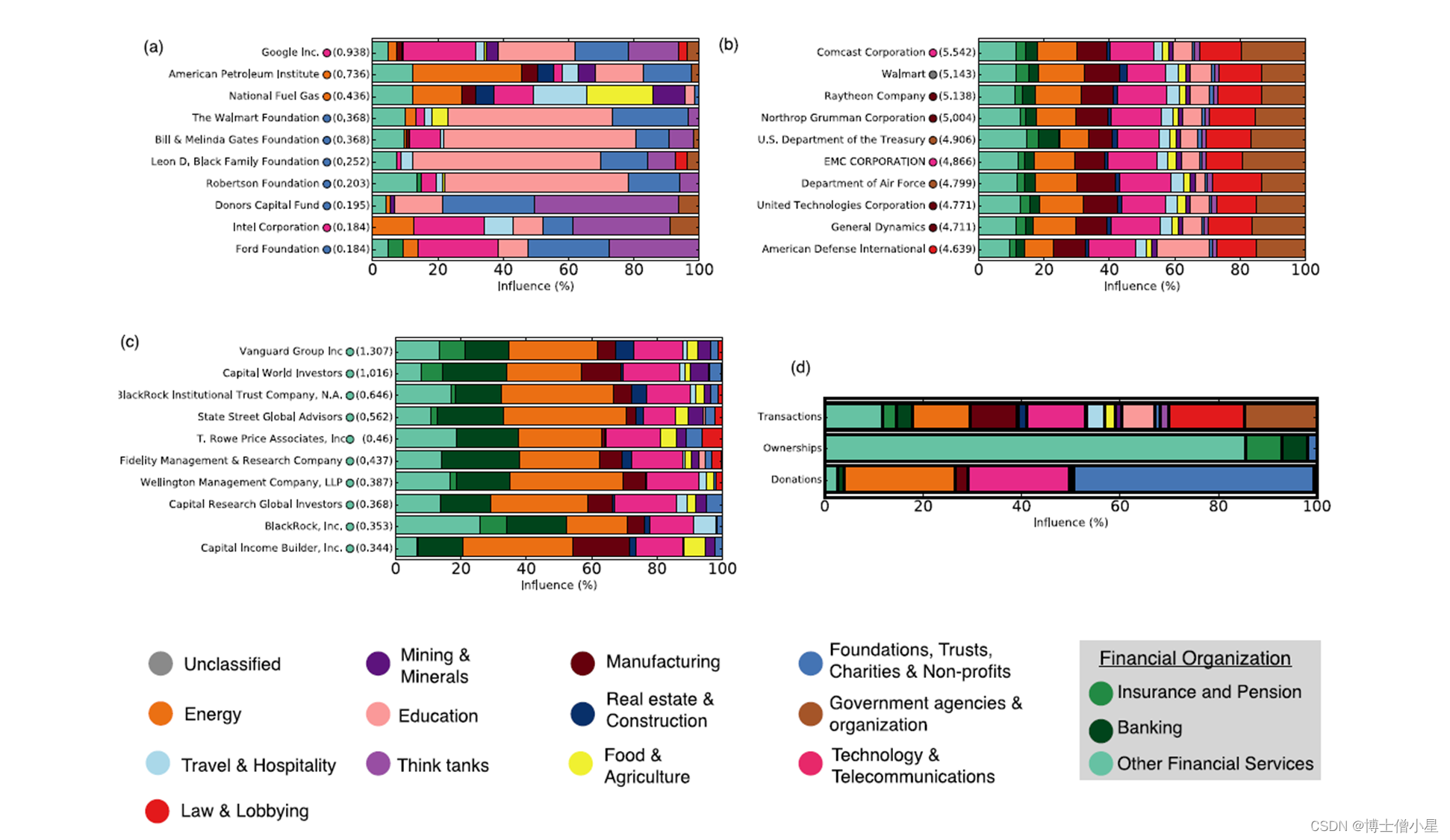
科研学习|论文解读——美国政治经济中的权力:网络分析(JASIST, 2019)
论文原题目 Power in the U.S. political economy: A network analysis 摘要 美国政治经济的许多特征产生于大型政治和经济机构之间的互动,然而我们对它们的互动性质和这些机构之间的权力分配知之甚少。在本文中,对总部设在美国的组织的网络进行了详细的…...

常用的git命令
一、常用的git命令 1. 配置 git config --local user.name "xxx" ---仅对当前Git仓库有效。配置信息将保存在当前Git仓库的 .git/config 文件中 local优先级最高,会覆盖其他范围的相同配置 git config --global user.email "xxx" ---全局…...

【AI】用iOS的ML(机器学习)创建自己的AI App
用iOS的ML(机器学习)创建自己的AI App 目录 用iOS的ML(机器学习)创建自己的AI App机器学习如同迭代过程CoreML 的使用方法?软件要求硬件开始吧!!构建管道:设计和训练网络Keras 转 CoreML将模型集成到 Xcode 中结论推荐超级课程: Docker快速入门到精通Kubernetes入门到…...

远程调用初体验笔记
远程调用初体验笔记 微服务架构通常将系统拆分成多个独立的服务单元,每个服务单元都专注于实现特定的业务功能。当一个服务需要使用另一个服务提供的功能时,就可以通过远程调用来实现。 使用步骤 1.步骤 Spring给我们提供了一个RestTemplate工具&#…...

反无人机电子护栏:原理、算法及简单实现
随着无人机技术的快速发展,其在航拍、农业、物流等领域的应用日益广泛。然而,无人机的不规范使用也带来了安全隐患,如侵犯隐私、干扰航空秩序等。为了有效管理无人机,反无人机电子护栏技术应运而生。 目录 一、反无人机电子护栏…...

Java项目利用Redisson实现真正生产可用高并发秒杀功能 支持分布式高并发秒杀
Java中的高并发秒杀场景下我们可以使用redisson来实现高并发秒杀功能, 以下就是一个可用于生产环境的高并发秒杀示例代码: pom依赖 <!-- https://mavenlibs.com/maven/dependency/org.redisson/redisson --><dependency><groupId>org.redisson</groupId&…...

0104行列式的性质-行列式-线性代数
记 D ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ a n 1 a n 2 ⋯ a n n ∣ D\begin{vmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\cdots&\cdots&&\cdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\en…...
)
k8s HPA 自动伸缩机制 (配置,资源限制,)
目录 一、概念 核心概念 工作原理 HPA 的配置关键参数 关键组件 使用场景 注意事项 如何确保程序稳定和服务连续 二、metrics-server 部署 metrics-server 准备 metrics-server 镜像: 使用 Helm 安装 metrics-server: 配置 metrics-server: 安装 metrics-server: …...

vulhub中GIT-SHELL 沙盒绕过漏洞复现(CVE-2017-8386)
GIT-SHELL 沙盒绕过(CVE-2017-8386)导致任意文件读取、可能的任意命令执行漏洞。 测试环境 为了不和docker母机的ssh端口冲突,将容器的ssh端口设置成3322。本目录下我生成了一个id_rsa,这是ssh的私钥,连接的时候请指…...

SpringBoot+vue3打造企业级一体化SaaS系统
SpringBootvue3打造企业级一体化SaaS系统 简介: 全面提升前后端技术水平,独立完成全栈项目开发能力,快速进击全栈工程师,最终在面试中脱颖而出。整合后端主流技术(Spring Boot、物理数据库隔离、加载动态权限、多…...
探讨TCP的可靠性以及三次握手的奥秘
🌟 欢迎来到 我的博客! 🌈 💡 探索未知, 分享知识 !💫 本文目录 1. TCP的可靠性机制1.2可靠性的基础上,尽可能得提高效率 2. TCP三次握手过程3. 为何不是四次握手? 在互联网的复杂世界中,TCP&am…...

openai常见的两个错误:BadRequestError和OpenAIError
错误1:openai.OpenAIError: The api_key client option must be set either by passing api_key..... 在通过openai创建客户端必须要设置api key,如果你事先已经在本机的环境中设置未起效可以手动设置,注意手动设置时不要用下面的形式 import openai f…...

2核4g服务器够用吗?
2核4G服务器够用吗?够用。阿腾云以2核4G5M服务器搭建网站为例,5M带宽下载速度峰值可达640KB/秒,阿腾云以搭建网站为例,假设优化后平均大小为60KB,则5M带宽可支撑10个用户同时在1秒内打开网站,并发数为10&am…...
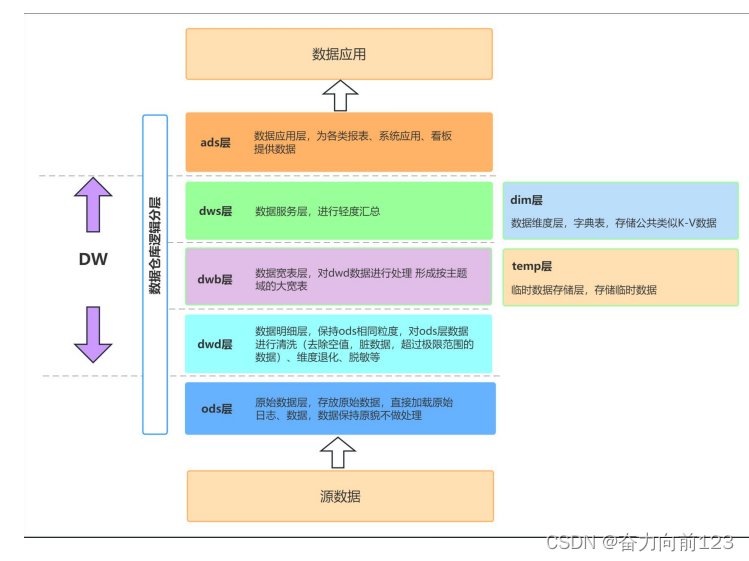
数据仓库数据分层详解
数据仓库中的数据分层是一种重要的数据组织方式,其目的是为了在管理数据时能够对数据有一个更加清晰的掌控。以下是数据仓库中的数据分层详解: 原始数据层(Raw Data Layer):这是数仓中最底层的层级,用于存…...
unity内存优化之AB包篇(微信小游戏)
1.搭建资源服务器使用(HFS软件(https://www.pianshen.com/article/54621708008/)) using System.Collections; using System.Collections.Generic; using UnityEngine;using System;public class Singleton<T> where T : class, new() {private static readonly Lazy<…...
白话模电:3.三极管(考研面试与笔试常考问题)
一、三极管的简单判断 1.判断三极 1)给了图 左边是b,有箭头是e,剩下是c 2)给了电位 b:中间值,e:较近值(离中间值),c:较远值(离中间值) 2.判断流向 bc同向(共同流向“|”或共同流离“|”),e与bc反向 3.判断材料 4.判断类型 5.判断能否构…...

LeetCode 395. 至少有K个重复字符的最长子串
解题思路 一道滑动窗口题型,不过滑动窗口的长度是不同种类元素的个数。 这里需要定义两个变量 cnt,overk。overk表示的是满足大于k的字符数, cnt表示的是该窗口中不同元素的个数且cnt>1&&cnt<26。 相关代码 class Solution {public int longestSub…...
C#重新认识笔记_ FixUpdate + Update
C#重新认识笔记_ FixUpdate Update Update: 刷新频率不一致,非物理对象的移动,简单的刷新可用, FixedUpdate: 刷新频率一致,按照固定频率刷新,一般调用FixedUpdate之后,会立即进入必要的物理计算中,因此,任何影响刚…...
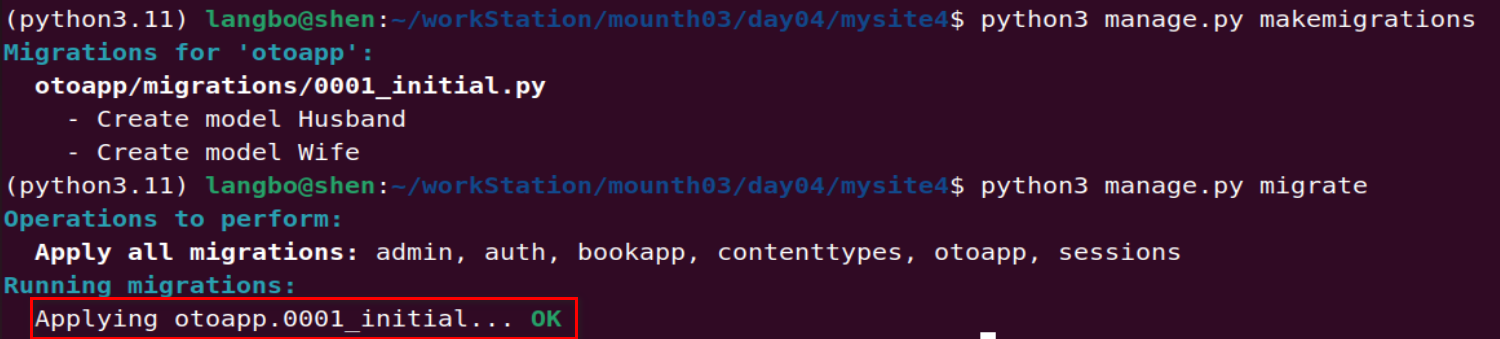
Django 解决新建表删除后无法重新创建等问题
Django 解决新建表删除后无法重新创建等问题 问题发生描述处理办法首先删除了app对应目录migrations下除 __init__.py以外的所有文件:然后,删除migrations中关于你的app的同步数据数据库记录最后,重新执行迁移插入 问题发生描述 Django创建的表…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...
