第 126 场 LeetCode 双周赛题解
A 求出加密整数的和

模拟
class Solution {
public:int sumOfEncryptedInt(vector<int> &nums) {int res = 0;for (auto x: nums) {string s = to_string(x);char ch = *max_element(s.begin(), s.end());for (auto &c: s)c = ch;res += stoi(s);}return res;}
};
B 执行操作标记数组中的元素


模拟:用堆维护元素中的最小元素,用数组记录元素是否被标记过,模拟对数组的操作过程
class Solution {
public:using ll = long long;vector<long long> unmarkedSumArray(vector<int> &nums, vector<vector<int>> &queries) {priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> heap;//最小堆int n = nums.size();for (int i = 0; i < n; i++)heap.emplace(nums[i], i);ll s = accumulate(nums.begin(), nums.end(), 0LL);vector<int> tag(n);vector<ll> res;for (auto &q: queries) {if (!tag[q[0]]) {//未被标记过tag[q[0]] = 1;s -= nums[q[0]];}for (int i = 0; i < q[1] && !heap.empty();) {//尽量标记ki个数组中还没有标记的最小元素auto [v, ind] = heap.top();heap.pop();if (tag[ind])continue;tag[ind] = 1;s -= v;i++;}res.push_back(s);}return res;}
};C 替换字符串中的问号使分数最小


贪心:记录 s s s 中各英文字母的出现次数,然后遍历 s s s ,遇到 ? ? ? 时将当前出现次数最小的英文字母放至该位置,同时该字母出现次数 + 1 +1 +1 ,最后对原字符串中所有 ? ? ? 处的字母进行排序,即得到满足条件的字符串
class Solution {
public:string minimizeStringValue(string s) {vector<int> cnt(26);string res;vector<char> li;vector<int> loc;int j = 0;for (auto c: s)if (c != '?')cnt[c - 'a']++;for (auto c: s) {if (c == '?') {int mn = *min_element(cnt.begin(), cnt.end());for (int i = 0; i < 26; i++)if (cnt[i] == mn) {cnt[i]++;li.push_back('a' + i);loc.push_back(j);break;}}j++;}sort(li.begin(), li.end());for (int i = 0; i < li.size(); i++)s[loc[i]] = li[i];return s;}
};
D 求出所有子序列的能量和


动态规划:设 p [ i + 1 ] [ j ] [ v ] p[i+1][j][v] p[i+1][j][v] 为字符串 n u m s [ 0 , i ] nums[0,i] nums[0,i] 中长度为 j j j 和为 v v v 的自序列的数目,因为 n u m s nums nums 任意一个长为 j j j 的子序列, n u m s nums nums 包含该子序列的子序列数目为 2 n − j 2^{n-j} 2n−j ,所以 n u m s nums nums 中所有子序列的能量和为 ∑ j = 1 n p [ n ] [ j ] [ k ] × 2 n − j \sum_{j=1}^n p[n][j][k]\times 2^{n-j} ∑j=1np[n][j][k]×2n−j
class Solution {
public:using ll = long long;int sumOfPower(vector<int> &nums, int k) {ll mod = 1e9 + 7;int n = nums.size();int p[n + 1][n + 1][k + 1];memset(p, 0, sizeof(p));p[0][0][0] = 1;for (int i = 0; i < n; i++) {p[i + 1][0][0] = 1;for (int j = 1; j <= i + 1; j++)for (int v = 1; v <= k; v++) {if (v - nums[i] >= 0)p[i + 1][j][v] = (p[i + 1][j][v] + p[i][j - 1][v - nums[i]]) % mod;p[i + 1][j][v] = (p[i + 1][j][v] + p[i][j][v]) % mod;}}vector<ll> pow(n);pow[0] = 1;for (int i = 1; i < n; i++)pow[i] = pow[i - 1] * 2 % mod;ll res = 0;for (int j = 1; j <= n; j++)if (p[n][j][k])res = (res + p[n][j][k] * pow[n - j]) % mod;return (res + mod) % mod;}
};
相关文章:

第 126 场 LeetCode 双周赛题解
A 求出加密整数的和 模拟 class Solution { public:int sumOfEncryptedInt(vector<int> &nums) {int res 0;for (auto x: nums) {string s to_string(x);char ch *max_element(s.begin(), s.end());for (auto &c: s)c ch;res stoi(s);}return res;} };B 执行…...
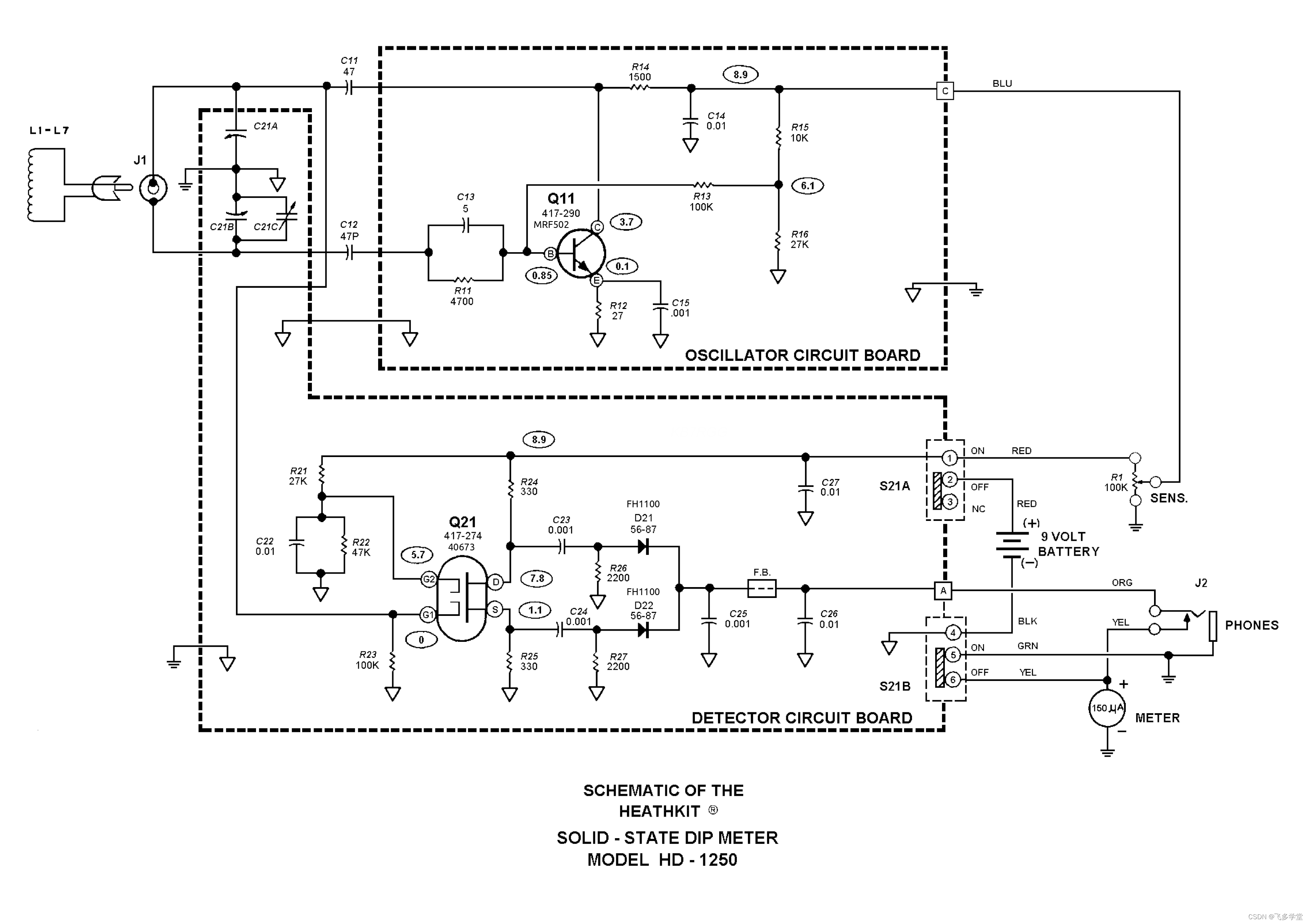
固态浸压计
Solid State Dip Meter(固态浸没仪/固态浸压计) 是真空管栅极浸入式仪表的固态半导体版本。它是一种用于测量 LC 电路谐振频率的仪器。LC 电路是由电感 (L) 和电容 (C) 组成的电路。当电感的感抗与电容的容抗相互抵消时,这些元件可以谐振于特定频率。 固态浸入式仪…...
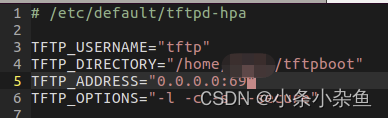
Ubuntu上搭建TFTP服务
Ubuntu上搭建TFTP服务 TFTP服务简介搭建TFTP服务安装TFTP服务修改配置文件 重启服务 TFTP服务简介 TFTP是一个基于UDP协议实现的用于在客户机和服务器之间进行简单文件传输的协议,适用于开销不大、不复杂的应用场合。TFTP协议专门为小文件传输而设计,只…...
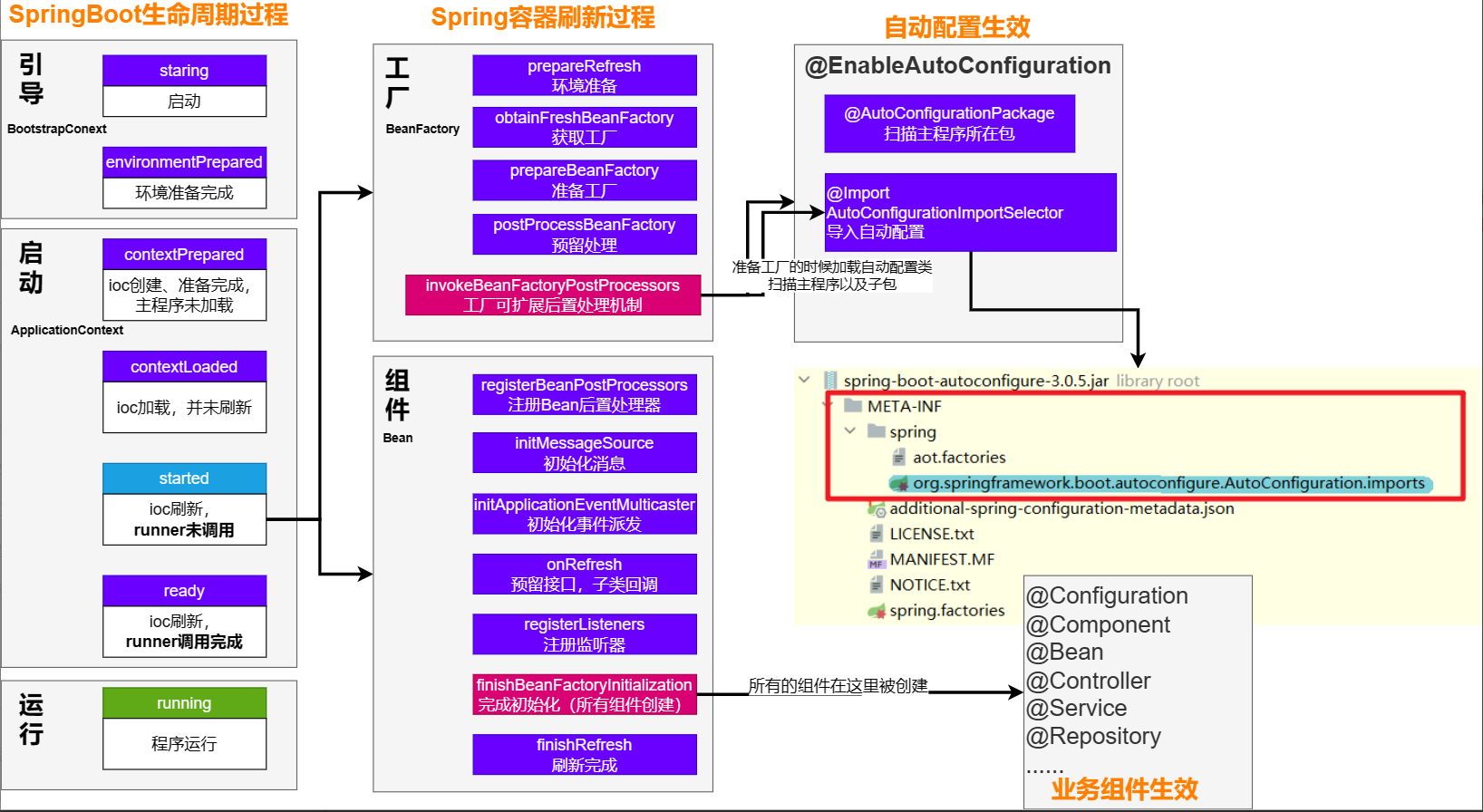
SpringBoot3框架,事件和监听器、SPI
事件和监听器 生命周期监听 自定义监听器的步骤: 编写SpringApplicationRunListener实现类(各个实现方法的功能写在其sout内) public class MyAppListener implements SpringApplicationRunListener {Overridepublic void starting(Configu…...
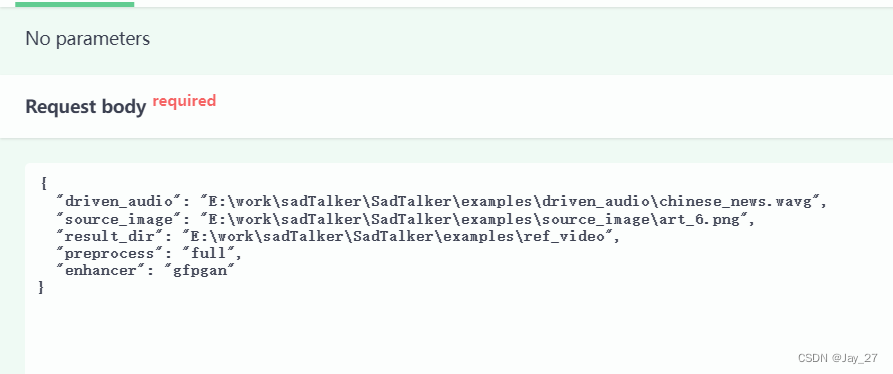
sadtalker-api/
———— 下载sadtalker工程文件,包括844个模型 。。。。。。。。。。。。。。。。 配置环境: pip源,设置: pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple anaconda prompt, 进入命令行 how在 …...

vue+elementUI实现指定列的单元格可编辑
template中的代码如下: <div v-if"(item.label 高压侧 || item.label 低压侧)&&coloumnHeader.label 单柱片数"><div class"editableCell"><div v-if"item.label 高压侧" dblclick"changeValue(sco…...
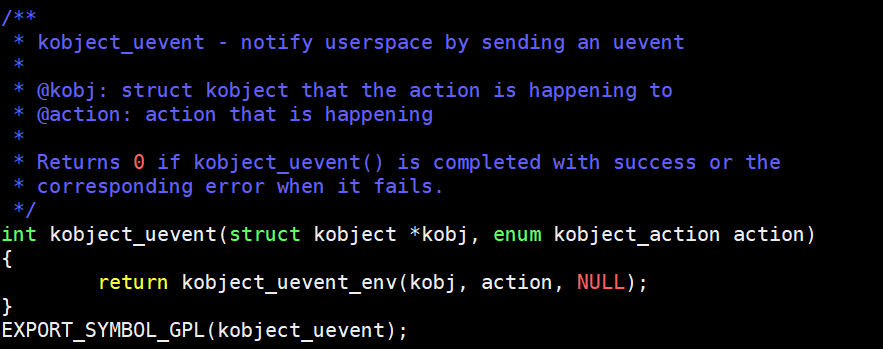
RK3568平台开发系列讲解(基础篇)内核是如何发送事件到用户空间
🚀返回专栏总目录 文章目录 一、相关接口函数二、udevadm 命令三、实验沉淀、分享、成长,让自己和他人都能有所收获!😄 一、相关接口函数 kobject_uevent 是 Linux 内核中的一个函数, 用于生成和发送 uevent 事件。 它是 udev 和其他设备管理工具与内核通信的一种方式。…...
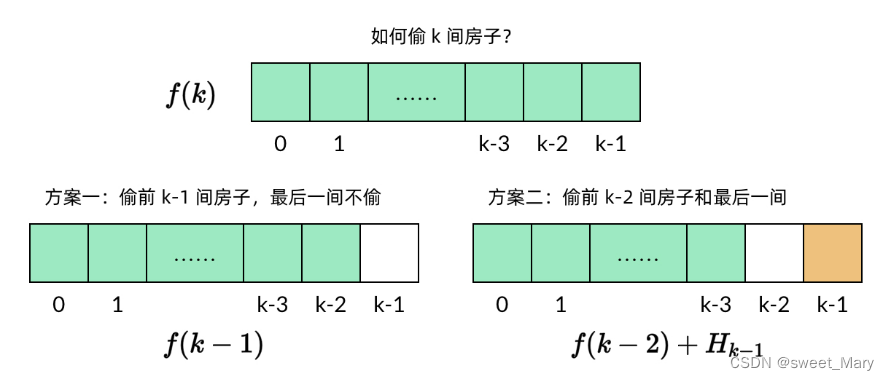
力扣---打家劫舍---动态规划
思路 1: 我将res[i]定义为:一定要取第 i 个房子的前提下,能获取的最大金额。那么直接用cnt从头记录到尾,每个房子的res最大值即是答案。那么递推公式是什么?res[i]max(res[i-2],res[i-1],...,res[0])nums[i]。数组初始…...

mac安装rust环境
mac安装rust环境 老规矩官方文档 1. mac官网使用的是脚本安装, 至于为啥没使用brew也没推荐俺也不太清楚 curl --proto https --tlsv1.2 -sSf https://sh.rustup.rs | sh2. 一般来说中途会遇见有一个选择我这里选择直接回车默认安装(如果以后我研究明白的话会进行更新, 现在是…...
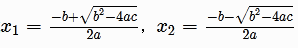
1058:求一元二次方程
【题目描述】 利用公式 求一元二次方程axbxc0的根,其中a不等于0。结果要求精确到小数点后5位。 【输入】 输入一行,包含三个浮点数a,b,c(它们之间以一个空格分开),分别表示方程axbxc0的系数。 【输出】 输出一行&…...

GraphQL入门之一对多关联查询
创建 Node.js 的工程 mkdir myapp cd myapp npm init (一路回车)安装依赖包 npm install apollo/server graphql定义 Schema 创建 schema.graphql 文件,内容如下: type Book {title: String!author: Author! }type Author {name: String!books: [Boo…...

MATLAB和Python数值和符号计算可视化物理学气体动能和粒子速度
要点 Python物理学差分数值和符号计算 热动力学计算:统计力学,分子动力学模型 Python寻找弹性物体的运动,LAMMPS 分子动力学模拟器模拟2D气体分子,Python原子模拟绘图,Python数值计算原子平衡性,Python绘制…...

阿里云-零基础入门NLP【基于机器学习的文本分类】
文章目录 学习过程赛题理解学习目标赛题数据数据标签评测指标解题思路TF-IDF介绍TF-IDF 机器学习分类器TF-IDF LinearSVCTF-IDF LGBMClassifier 学习过程 20年当时自身功底是比较零基础(会写些基础的Python[三个科学计算包]数据分析),一开始看这块其实挺懵的&am…...
蓝桥杯模块综合——高质量讲解AT24C02,BS18B20,BS1302,AD/DA(PCF8591),超声波模块
AT24C02——就是一个存储的东西,可以给他写东西,掉电不丢失。 void EEPROM_Write(unsigned char * EEPROM_String,unsigned char addr , unsigned char num) {IIC_Start();IIC_SendByte(0xA0);IIC_WaitAck();IIC_SendByte(addr);IIC_WaitAck();while(nu…...

前端跨平台开发框架:简化多端开发的利器
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...
cesium.js加载模型后,重新设置旋转角度属性值
// 加载模型var position Cesium.Cartesian3.fromDegrees(longitude, latitude, height);// 计算矩阵var rollAngleDegrees 15; // 设置翻滚角度var rollAngleRadians Cesium.Math.toRadians(rollAngleDegrees); // 将角度转换为弧度var orientation Cesium.Transforms.eas…...
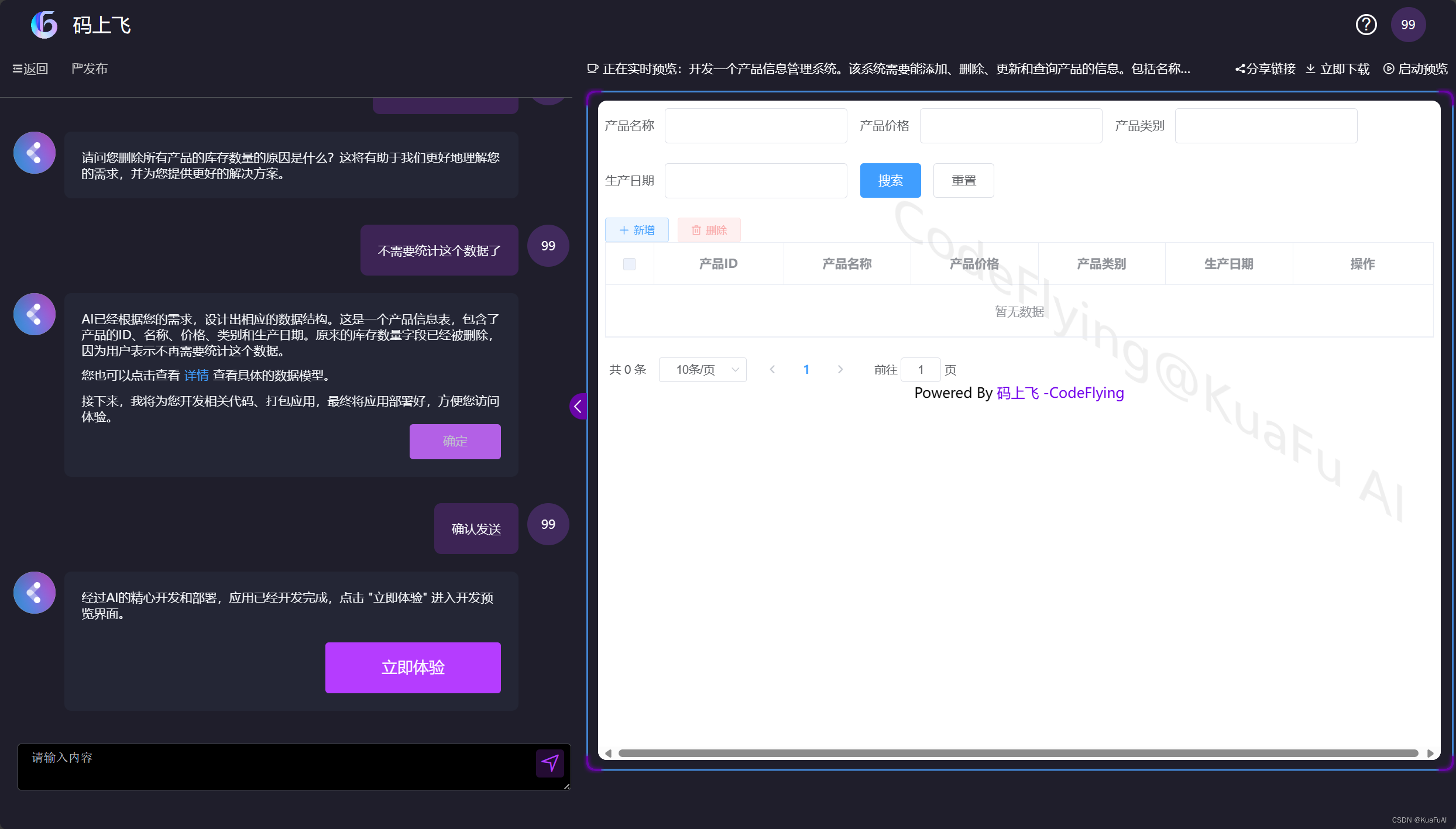
②免费AI软件开发工具测评:通义灵码 VS 码上飞
前言 我又双叒叕来测评了!上次给大家带来的是iFlyCode和CodeFlying两款产品的测评,受到了大家的一致好评~ 今天咱就继续来聊聊,这次我们选的的对象是通义灵码和码上飞,从名字上也能看到出来这两款产品一定是跟软件开发有关系的&…...
幻兽帕鲁游戏搭建(docker)
系列文章目录 第一章: 幻兽帕陆游戏搭建 文章目录 系列文章目录前言一、镜像安装1.创建游戏目录2.拉取镜像3.下载配置文件4.启动游戏 二、自定义配置总结 前言 这段时间一直在写论文还有找工作,也没学啥新技术,所以博客也很长时间没写了&am…...
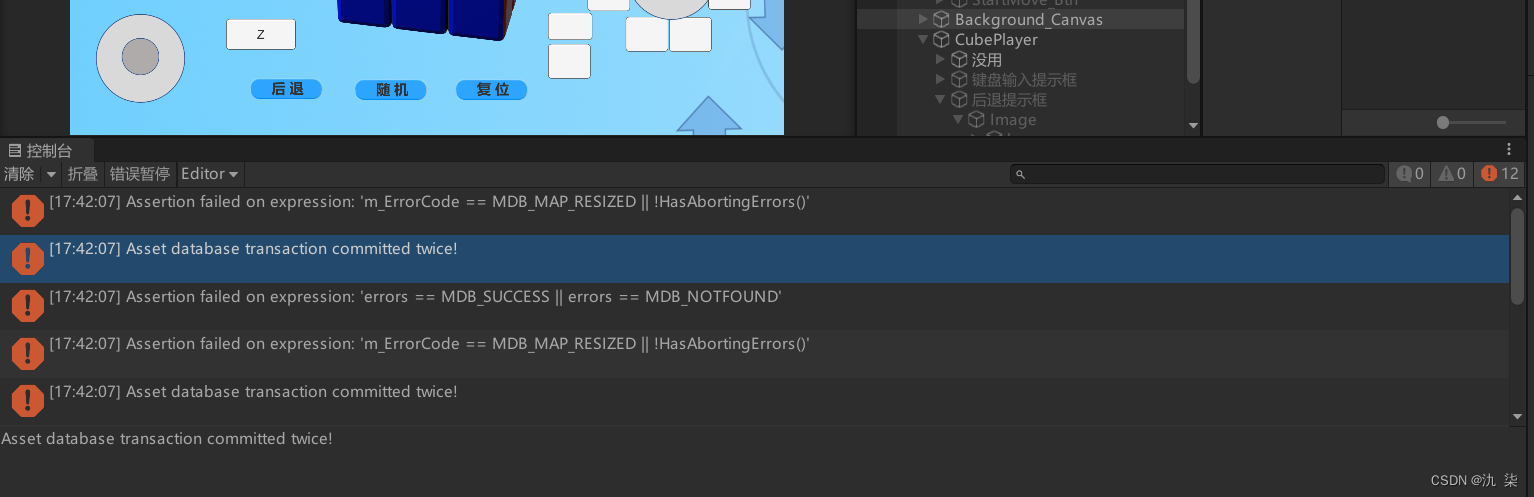
unity报错出现Asset database transaction committed twice!
错误描述: 运行时报错 Assertion failed on expression: ‘m_ErrorCode MDB_MAP_RESIZED || !HasAbortingErrors()’Asset database transaction committed twice!Assertion failed on expression: ‘errors MDB_SUCCESS || errors MDB_NOTFOUND’ 解决办法&…...

去除项目git的控制 端口号的关闭
以下操作都是在windows下。只是记录一下。 find . -name “.git” | xargs rm -rf 查看所有分支 git branch -a 查看当前分支 git branch -a 切换分支 git chenkout develop docker 查看容器的ip docker inspect -f ‘{{.Name}} - {{range .NetworkSettings.Networks}}{{.IP…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
