<Senior High School Math>: inequality question

( 1 ) . o m i t (1). omit (1).omit
( 2 ) . ( a 2 − b 2 ) ( x 2 a 2 − y 2 b 2 ) = ( x 2 + y 2 ) − ( a 2 y 2 b 2 + b 2 x 2 a 2 ) ≤ x 2 + y 2 − 2 x y = ( x − y ) 2 (2). (a^2-b^2)(\frac{x^2}{a^2} - \frac{y^2}{b^2})=(x^2+y^2)-(\frac{a^2y^2}{b^2}+\frac{b^2x^2}{a^2}) \le x^2+y^2-2xy=(x-y)^2 (2).(a2−b2)(a2x2−b2y2)=(x2+y2)−(b2a2y2+a2b2x2)≤x2+y2−2xy=(x−y)2
- when a y b = b x a \frac{ay}{b}=\frac{bx}{a} bay=abx, the equation is satisfied.
( 3 ) . (3). (3). s e t : 3 m − 5 = x , m − 2 = y set: \sqrt{3m-5}=x,\sqrt{m-2}=y set:3m−5=x,m−2=y
t h e n : x 2 − 3 y 2 = 1 then: x^2-3y^2=1 then:x2−3y2=1
h a v e : x 2 1 − y 2 1 3 = 1 , have:\frac{x^2}{1}-\frac{y^2}{\frac{1}{3}}=1, have:1x2−31y2=1, according to the question(2), we get:
( x − y ) 2 ≥ ( 1 − 1 3 ) ( x 2 1 − y 2 1 3 ) = 2 3 (x-y)^2 \ge (1-\frac{1}{3})(\frac{x^2}{1}-\frac{y^2}{\frac{1}{3}})=\frac{2}{3} (x−y)2≥(1−31)(1x2−31y2)=32
- Pay attention to equal conditions!!!
- we can click here to see some more examples about the Cauchy-inequality.
相关文章:

<Senior High School Math>: inequality question
( 1 ) . o m i t (1). omit (1).omit ( 2 ) . ( a 2 − b 2 ) ( x 2 a 2 − y 2 b 2 ) ( x 2 y 2 ) − ( a 2 y 2 b 2 b 2 x 2 a 2 ) ≤ x 2 y 2 − 2 x y ( x − y ) 2 (2). (a^2-b^2)(\frac{x^2}{a^2} - \frac{y^2}{b^2})(x^2y^2)-(\frac{a^2y^2}{b^2}\frac{b^2x^2}{a^…...

详解Python中Pytest和Unittest的区别
昨天在群里面,有两个新手的小伙伴提问:Pytest 和 Unittest是Python中属于最常用的两个测试框架。那么他们有些什么区别呢? Playwright 为什么只给了Pytest的深度支持,而不是Unittest呢? 这是个好问题, 田辛…...
-音频基础)
零基础入门多媒体音频(1)-音频基础
声音的本质是波动,波形图能直观体现声音的特征。我们常用于描述音频的属性有下面这些: 1.采样率:声音中每秒包含的采样点个数。 2.位宽:每个采样点需要多少个bit进行存储。 3.声道数:声音进行回放需要喇叭的个数。 4.频…...

40 道高频 C++ 面试、笔试题及答案
1. 什么是多态? 答案: 多态允许对象在运行时表现出不同的行为,具体取决于其类型。 2. 虚函数和纯虚函数之间的区别是什么? 答案: 虚函数可以被派生类重写,而纯虚函数必须被派生类实现,否则派生…...
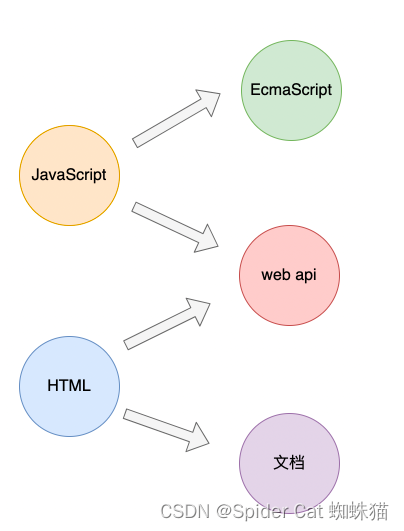
【07】进阶html5
HTML5 包含两个部分的更新,分别是文档和web api 文档 HTML5 元素表 元素语义化 元素语义化是指每个 HTML 元素都代表着某种含义,在开发中应该根据元素含义选择元素 元素语义化的好处: 利于 SEO(搜索引擎优化)利于无障碍访问利于浏览器的插件分析网页新增元素 多媒体…...
)
Linux|centos7|postgresql数据库|yum和编译方式安装总结(全系版本)
一、 yum方式安装postgresql 这个是官方的yum源,包括postgresql的开发包,lib库什么的,很齐全,关键是包括pgbackrest yum install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-7-x86_64/pgdg-redhat-repo-la…...
---STL容器(set/multiset、map/multimap))
C++提高笔记(五)---STL容器(set/multiset、map/multimap)
1、set / multiset容器 1.1set基本概念 简介:所有元素都会在插入时自动被排序 本质:set和multiset属于关联式容器,底层结构是用二叉树实现 set和multiset区别: set不允许容器中有重复的元素 multiset允许容器中有重复的元素 …...
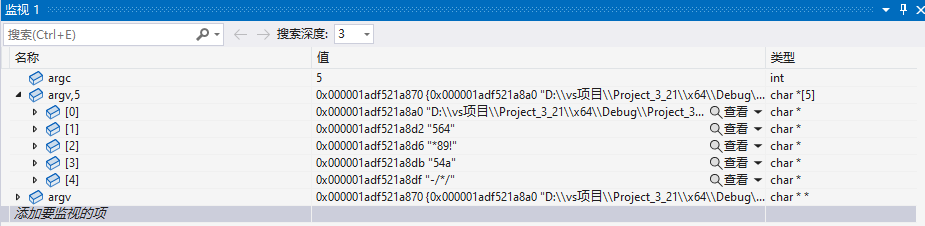
详解main函数参数argc、argv及如何传参
目录 1、main()函数参数 2、main函数如何传参 2.1 环境准备 2.2 通过 Powershell 窗口传参 2.3 通过vs界面传参 3、int main() 和 int main(int argc, char *argv[]) 特点 1、main()函数参数 在C语言中,main函数可以带参数。main函数的原型通常为以下两种形式…...

解释什么是Web组件化开发及其优势
解释什么是Web组件化开发及其优势 Web组件化开发,是一种将Web应用的界面和功能拆分为独立、可复用的组件的开发方法。这种方法的核心思想是将大型、复杂的Web应用拆分为一系列小型、功能单一的组件,每个组件都负责处理特定的业务逻辑或界面表现。通过组…...

那些场景需要额外注意线程安全问题
主要学习那些场景需要额外注意线程安全问题,在这里总结了四中场景。 访问共享变量或资源 第一种场景是访问共享变量或共享资源的时候,典型的场景有访问共享对象的属性,访问static静态变量,访问共享的缓存,等等。因为…...
球球大作战)
(C语言)球球大作战
前言: 这款简易版的球球大作战是一款单人游戏,玩家需要控制一个小球在地图上移动,吞噬其他小球来增大自己的体积。本游戏使用C语言和easyx图形库编写,旨在帮助初学者了解游戏开发的基本概念和技巧。 在开始编写代码之前…...

高级数据结构 <AVL树>
本文已收录至《数据结构(C/C语言)》专栏! 作者:ARMCSKGT 目录 前言正文AVL树的性质AVL树的定义AVL树的插入函数左单旋右单旋右左双旋左右双旋 检验AVL树的合法性关于AVL树 最后 前言 前面我们学习了二叉树,普通的二叉树没有任何特殊性质&…...

在springboot中利用Redis实现延迟队列
文章目录 前言一、基本思路二、springboot实现案例三、测试总结 前言 在开发过程中,有很多场景都需要用到延迟队列来解决。目前支持延迟队列的中间件也不少,特别是基于JMS模式下的消息中间件基本上都支持延迟队列。但是有时我们项目规模可能比较小&…...

UpGrow评论:AI能将我的Instagram粉丝数增加10倍吗?
UpGrow Review: Can AI Grow My Instagram Followers 10X? 概述 UpGrow是一款专注于Instagram增长的AI驱动型社交媒体工具。它通过其庞大的300多人的网络,先进的定位功能,实时分析以及卓越的客户服务,帮助用户有机地增长Instagram关注者。…...

申请软著提交的演示视频有什么要求
申请软件著作权时,演示视频是一个重要的材料,主要用于展示软件的功能和操作流程。演示视频的要求可能会根据不同的申请机构和项目有所不同,但一般来说,以下是几个常见的要求: 内容完整性:演示视频需要展示…...
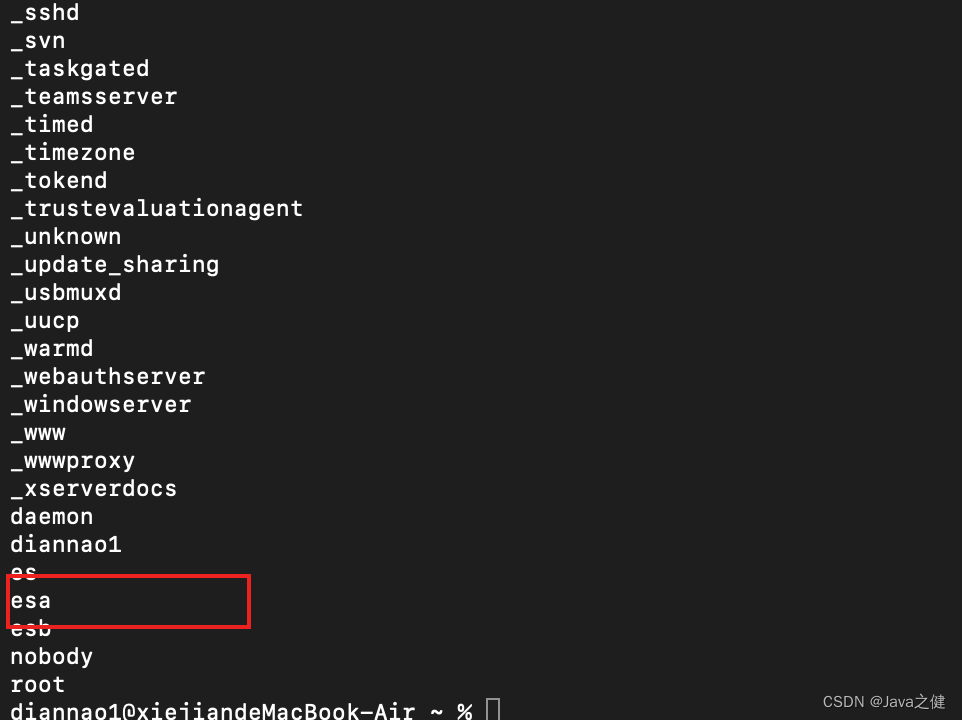
mac【启动elasticsearch报错:can not run elasticsearch as root
mac【启动elasticsearch报错:can not run elasticsearch as root 问题原因 es默认不能用root用户启动,生产环境建议为elasticsearch创建用户。 解决方案 为elaticsearch创建用户并赋予相应权限。 尝试了以下命令创建用户,adduser esh 和u…...
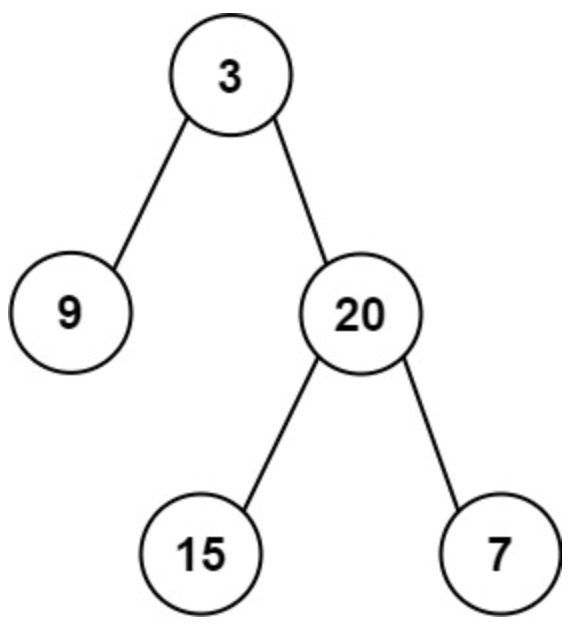
面试算法-65-二叉树的层平均值
题目 给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:[3.00000,14.50000,11.00000] 解释:第 0 层的…...

Linux: boot: latency启动延迟分析
https://elinux.org/images/6/64/Chris-simmonds-boot-time-elce-2017_0.pdf https://www.hcltech.com/sites/default/files/documents/resources/whitepaper/files/an_insight_to_optimize_embedded_linux_boot_time_performance.pdf 无意看到这个启动延迟分析,虽…...

QT界面制作
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);this->setWindowFlag(Qt::FramelessWindowHint);//接收动图QMovie *mv new QMovie(":/pictrue/th.gif…...
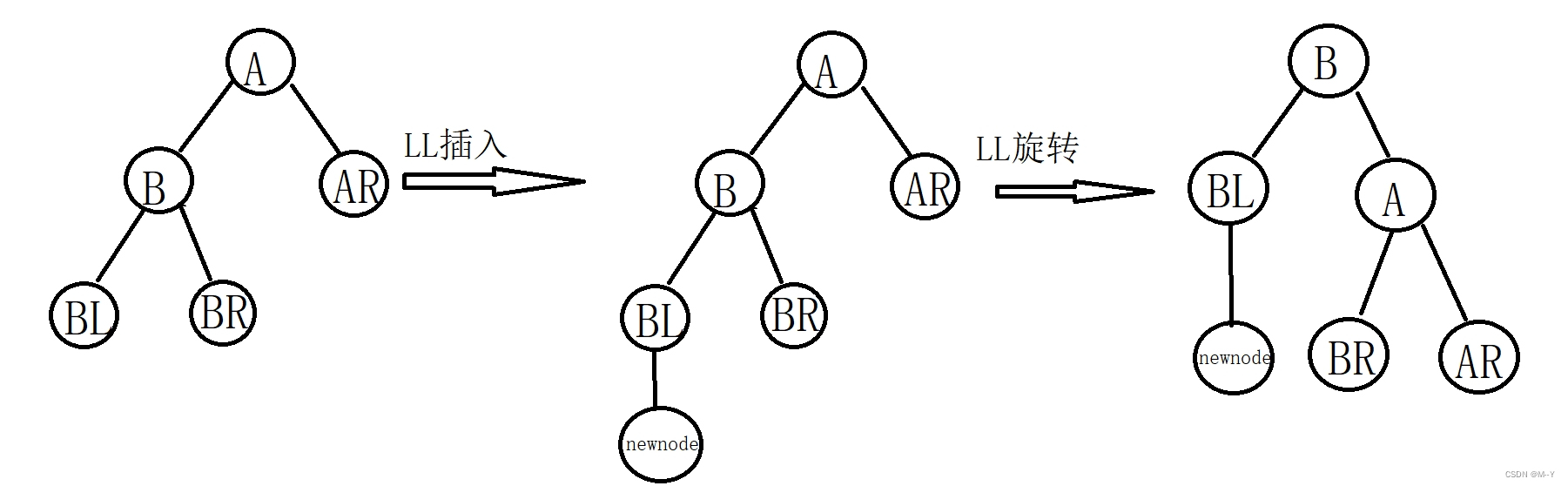
进阶二叉树
目录 二叉树 二叉搜索树 二叉搜索树的定义 二叉搜索树的操作 哈夫曼树 哈夫曼树的定义 哈夫曼树的构造 哈夫曼树的性质 平衡二叉树 平衡二叉树的定义: 平衡二叉树的插入调整 1.LL插入/LL旋转 2.RR插入/RR旋转 3.LR插入/LR旋转 4.RL插入/RL旋转 二叉树…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...
