每日OJ题_子数组子串dp⑥_力扣978. 最长湍流子数组
目录
力扣978. 最长湍流子数组
解析代码
力扣978. 最长湍流子数组
978. 最长湍流子数组
难度 中等
给定一个整数数组 arr ,返回 arr 的 最大湍流子数组的长度 。
如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是 湍流子数组 。
更正式地来说,当 arr 的子数组 A[i], A[i+1], ..., A[j] 满足仅满足下列条件时,我们称其为湍流子数组:
- 若
i <= k < j:- 当
k为奇数时,A[k] > A[k+1],且 - 当
k为偶数时,A[k] < A[k+1];
- 当
- 或 若
i <= k < j:- 当
k为偶数时,A[k] > A[k+1],且 - 当
k为奇数时,A[k] < A[k+1]。
- 当
示例 1:
输入:arr = [9,4,2,10,7,8,8,1,9] 输出:5 解释:arr[1] > arr[2] < arr[3] > arr[4] < arr[5]
示例 2:
输入:arr = [4,8,12,16] 输出:2
示例 3:
输入:arr = [100] 输出:1
提示:
1 <= arr.length <= 4 * 10^40 <= arr[i] <= 10^9
class Solution {
public:int maxTurbulenceSize(vector<int>& arr) {}
};解析代码
题意的湍流数组就是一上一下的意思,只有一个元素时长度为1。
先尝试定义状态表示为:dp[i] 表示以 i 位置为结尾的最长湍流数组的长度。
但是,问题来了,如果状态表示这样定义的话,以 i 位置为结尾的最长湍流数组的长度我们没法从之前的状态推导出来。因为我们不知道前一个最长湍流数组的结尾处是递增的,还是递减的。因此,我们需要状态表示能表示多一点的信息:要能让我们知道这一个最长湍流数组的结尾是递增的还是递减的。
因此需要两个 dp 表:
- f[i] 表示:以i位置元素为结尾的所有子数组中,最后呈现上升状态下的最⻓湍流数组的⻓度。
- g[i] 表示:以i位置元素为结尾的所有子数组中,最后呈现下降状态下的最⻓湍流数组的⻓。
状态转移方程: 对于 i 位置的元素 arr[i] ,有下面两种情况:
- arr[i] > arr[i - 1] :如果 i 位置的元素比 i - 1 位置的元素大,说明接下来 应该去找 i -1 位置结尾,并且 i - 1 位置元素比前⼀个元素小的序列,那就是 g[i - 1] 。更新 f[i] 位置的值: f[i] = g[i - 1] + 1 ;
- arr[i] < arr[i - 1] :如果 i 位置的元素比 i - 1 位置的元素小,说明接下来 应该去找 i - 1 位置结尾,并且 i - 1 位置元素比前⼀个元素大的序列,那就是 f[i - 1] 。更新 g[i] 位置的值: g[i] = f[i - 1] + 1;
- arr[i] == arr[i - 1] :不构成湍流数组。
初始化: 所有的元素单独都能构成一个湍流数组,因此可以将 dp 表内所有元素初始化为 1。 由于用到前面的状态,因此循环的时候从第二个位置开始。
从左往右,两个表一起填,最后返回两个dp表中的最大值即可。
class Solution {
public:int maxTurbulenceSize(vector<int>& arr) {int n = arr.size(), ret = 1;vector<int> f(n, 1), g(n, 1);// 以i位置元素为结尾的所有子数组中,呈现上升/下降状态下的最⻓湍流数组的⻓度for(int i = 1; i < n; ++i){if(arr[i-1] > arr[i]) // 下降的{g[i] = f[i-1] + 1; }else if(arr[i-1] < arr[i]) // 上升的{f[i] = g[i-1] + 1; }ret = max(ret, max(f[i], g[i]));}return ret;}
};相关文章:

每日OJ题_子数组子串dp⑥_力扣978. 最长湍流子数组
目录 力扣978. 最长湍流子数组 解析代码 力扣978. 最长湍流子数组 978. 最长湍流子数组 难度 中等 给定一个整数数组 arr ,返回 arr 的 最大湍流子数组的长度 。 如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是 湍流子数组 。 更正…...

蓝桥练习题总结(一)字母图形、完美的代价、01串、序列求和
目录 一、字母图形 二、完美的代价 三、01字串 四、序列求和 一、字母图形 问题描述 利用字母可以组成一些美丽的图形,下面给出了一个例子: ABCDEFG BABCDEF CBABCDE DCBABCD EDCBABC 这是一个5行7列的图形,请找出这个图形的规律ÿ…...
)
Android 静默安装二(无障碍服务版)
近期开发上线一个常驻app,项目已上线,今天随笔记录一下静默安装相关内容。我分三篇静默安装(root版)、静默安装(无障碍版)、监听系统更新、卸载、安装。 先说说我的项目需求:要求app一直运行&am…...
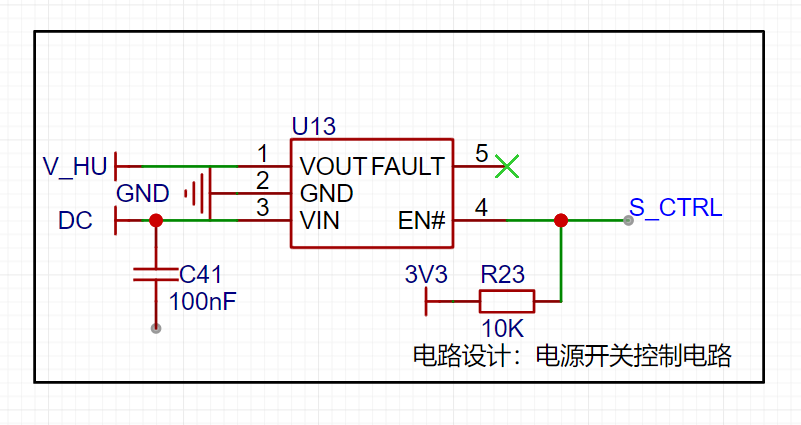
蓝桥杯 EDA 组 2023模拟+真题原理图解析
本文解析了标题内的原理图蓝桥杯EDA组真题,2021-2022 省赛真题/模拟题在上一篇文中。本文中重复或者是简单的电路节约篇幅不在赘述。 其中需要补充和计算原理图的题目解析都放在最下面 一、2023 年第十四届省赛模拟题1 1.1 Type-C 接口电路 通过 CH340N 将数据转化为…...
)
聊聊功率器件(氮化镓,碳化硅)
氮化镓和碳化硅是两种具有独特性质和广泛应用的无机物。下面将尽可能详细地解释它们的定义、应用、研究热点以及对我们的价值。 1,氮化镓 氮化镓(GaN)是一种由氮和镓元素组成的化合物,具有直接能隙的半导体特性。其结构类似于纤…...
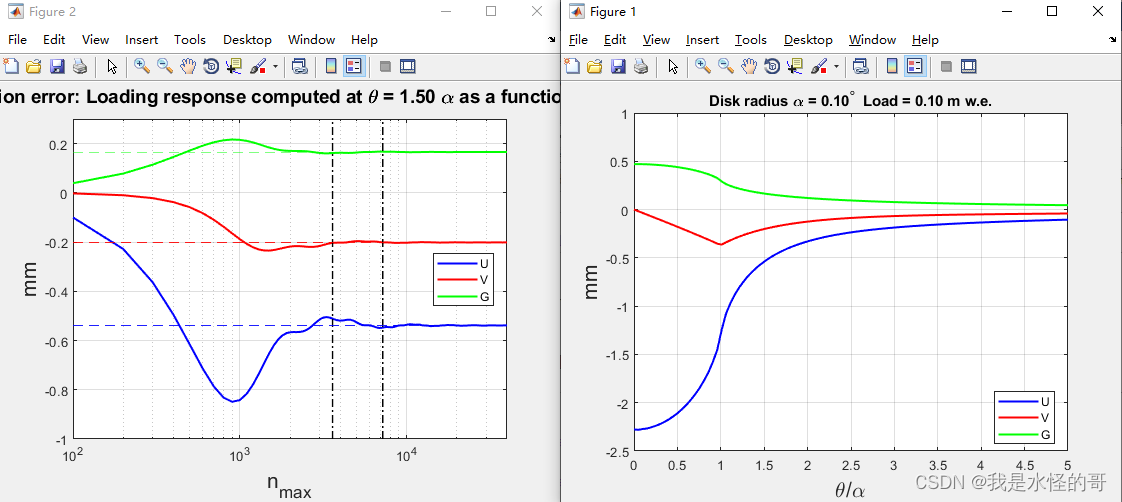
计算地球圆盘负荷产生的位移
1.研究背景 计算受表面载荷影响的弹性体变形问题有着悠久的历史,涉及到许多著名的数学家和物理学家(Boussinesq 1885;Lamb 1901;Love 1911,1929;Shida 1912;Terazawa 1916;Munk &…...

Harbor介绍
1.什么是Harbor Harbor是一个开源的企业级Docker Registry管理项目,由VMware公司开源。 Harbor提供了比Docker官方公共镜像仓库更为丰富和安全的功能,尤其适合企业环境使用。以下是Harbor的一些关键特性: 权限管理(RBAC&#x…...
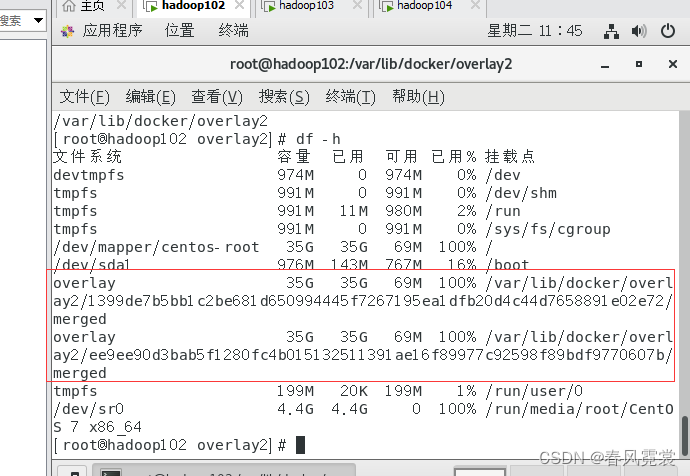
解决jenkins运行磁盘满的问题
参考:https://blog.csdn.net/ouyang_peng/article/details/79225993 分配磁盘空间相关操作: https://cloud.tencent.com/developer/article/2230624 登录jenkins相对应的服务或容器中查看磁盘情况: df -h在102挂载服务器上看到是这两个文件…...

使用echart绘制拓扑图,树类型,自定义tooltip和label样式,可收缩
效果如图: 鼠标移上显示 vue3 - ts文件 “echarts”: “^5.4.3”, import { EChartsOption } from echarts import * as echarts from echarts/core import { TooltipComponent } from echarts/components import { TreeChart } from echarts/charts import { C…...

常用的6个的ChatGPT网站,国内可用!
GPTGod 🌐 链接: GPTGod 🏷️ 标签: GPT-4 免费体验 支持API 支持绘图 付费选项 📝 简介:GPTGod 是一个功能全面的平台,提供GPT-4的强大功能,包括API接入和绘图支持。用户可以选择免…...

Linux课程____Samba文件共享服务
一、 Samba服务基础 SMB协议,服务消息块 CIFS协议,通用互联网文件系统 1.Samba 服务器的主要程序 smbd:提供对服务器中文件、打印资源的共享访问 nmbd:提供基于 NetBlOS 主机名称的解析 2.目录文件 /etc/samba/smb.conf 检查工具:test…...

Java学习day1
打开命令提示符(cmd)窗口: 按下winR键,输入cmd 按回车或点击确定,打开cmd窗口 常用cmd命令 盘符名称冒号(D:):盘符切换,示例表示由C盘切换到D盘 dir:查看当前路径下的内…...

ByteTrack多目标跟踪——YOLOX详解
文章目录 1 before train1.1 dataset1.2 model 2 train2.1 Backbone2.2 PAFPN2.3 Head2.3.1 Decoupled Head2.3.2 anchor-free2.3.3 标签分配① 初步筛选② simOTA 2.3.4 Loss计算 项目地址: ByteTrack ByteTrack使用的检测器是YOLOX,是一个目前非常流行…...
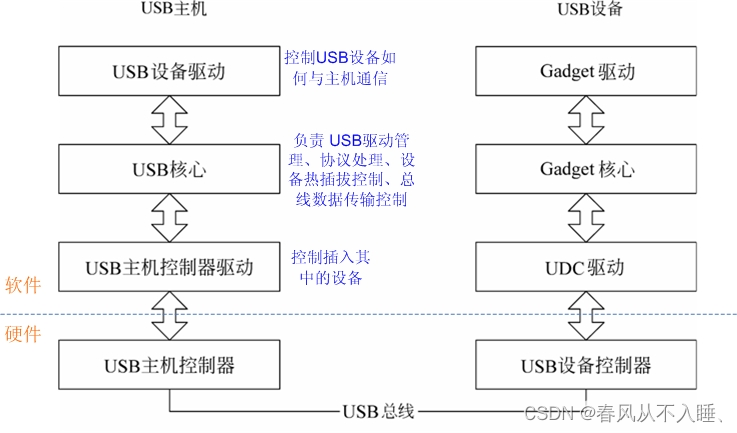
Linux 常见驱动框架
一、V4L2驱动框架 v4l2驱动框架主要对象: (1)video_device:一个字符设备,为用户空间提供设备节点(/dev/videox),提供系统调用的相关操作(open、ioctl…) (2)v4l2_device:…...
)
Oracle函数6—递归查询(start with...connect by、sys_connect_by_path、level)
文章目录 一、准备数据二、基本使用三、level函数四、获取完整的全树路径 一、准备数据 创建表 CREATE TABLE TEST_ORG (ID VARCHAR2(64) NOT NULL PRIMARY KEY,NAME VARCHAR2(200),PARTEN_ID VARCHAR2(64) ); comment on column TEST_ORG.ID is 主键; comment on column TES…...
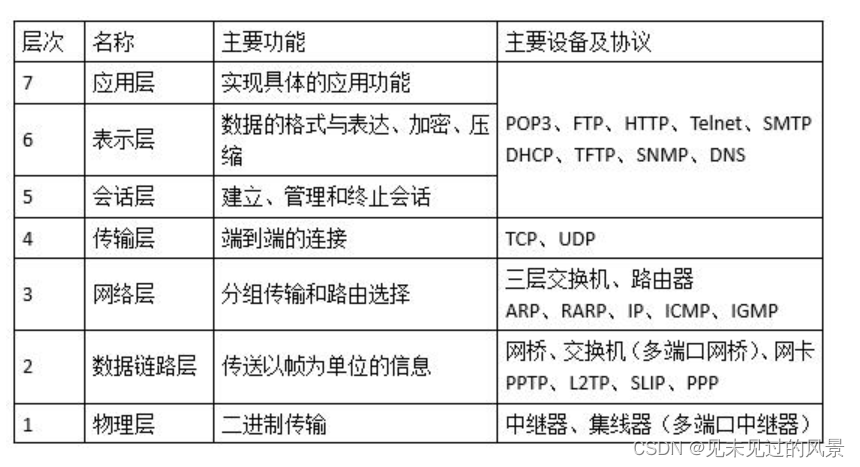
人机交互三原则,网络7层和对应的设备、公钥私钥
人机交互三原则 heo Mandel提出了人机交互的三个黄金原则,它们强调了相似的设计目标,分别是: 简单总结为:控负持面–>空腹吃面 1,用户控制 2,减轻负担 3,保持界面一致 置用户于控制之下&a…...
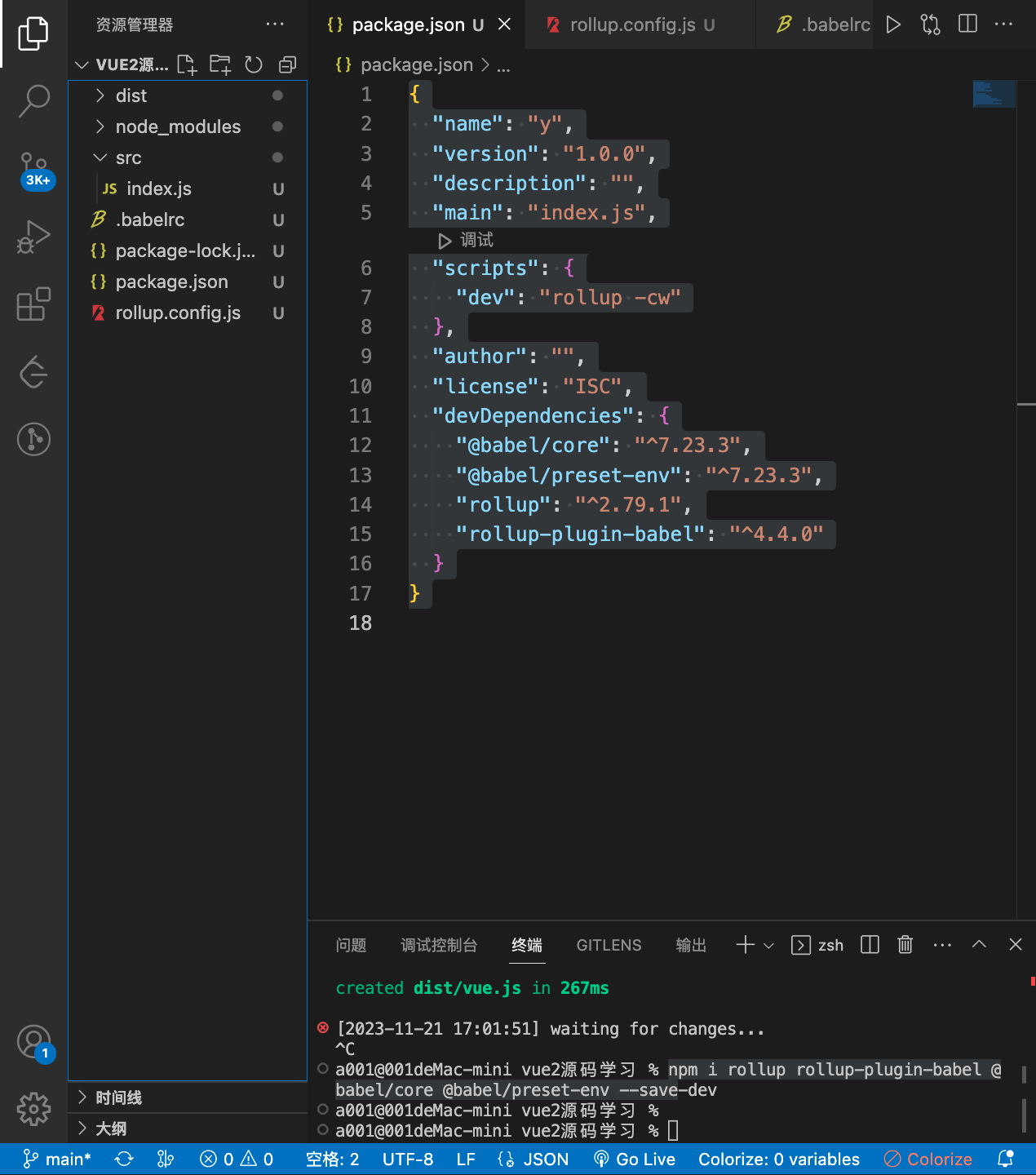
vue2源码学习01配置rollup打包环境
1.下载rollup相关依赖 npm i rollup rollup-plugin-babel babel/core babel/preset-env --save-dev 2.新建rollup.config.js配置打包选项 //rollup可以导出一个对象,作为打包的配置文件 import babel from rollup-plugin-babel export default {input: ./src/ind…...
DP:斐波那契数列模型
创作不易,感谢三连支持 ! 斐波那契数列用于一维探索的单峰函数之中,用于求解最优值的方法。其主要优势为,在第一次迭代的时候求解两个函数值,之后每次迭代只需求解一次 。 一、第N个泰波那契数 . - 力扣(…...
----prmise)
JavaScript高级(十四)----prmise
异步请求的处理方式 回调函数 所谓的回调函数就是函数作为参数的传递,在一个函数内部调用另一个函数,调用的同时可以把内部函数的数据传递出来,他的使用场景就是异步操作,数据需要等待一段时间才能返回的情况下可以使用回调函数…...

28 OpenCV 轮廓周围绘制图形
文章目录 approxPolyDP 轮廓周围绘制矩形boundingRectminAreaRect绘制圆和椭圆示例 approxPolyDP 轮廓周围绘制矩形 approxPolyDP(InputArray curve, OutputArray approxCurve, double epsilon, bool closed)curve:输入点集,二维点向量的集合appro…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
