聚类分析|基于层次的聚类方法及其Python实现
聚类分析|基于层次的聚类方法及其Python实现
- 0. 基于层次的聚类方法
- 1. 簇间距离度量方法
- 1.1 最小距离
- 1.2 最大距离
- 1.3 平均距离
- 1.4 中心法
- 1.5 离差平方和
- 2. 基于层次的聚类算法
- 2.1 凝聚(Agglomerative)
- 2.3 分裂(Divisive)
- 3. 基于层次聚类算法的Python实现
0. 基于层次的聚类方法
层次聚类(Hierarchical Clustering)类似于一个树状结构,对数据集采用某种方法逐层地进行分解或者汇聚,直到分出的最后一层的所有类别数据满足要求为止。
当数据集不知道应该分为多少类时,使用层次聚类比较适合。
无论是凝聚方法还是分裂方法,一个核心问题是度量两个簇之间的距离,其中每个簇是一个数据样本集合。
划分方法(Partitioning Method)是基于距离判断样本相似度,通过不断迭代将含有多个样本的数据集划分成若干个簇,使每个样本都属于且只属于一个簇,同时聚类簇的总数小于样本总数目。如k-means和k-medoids。 该方法需要事先给定聚类数以及初始聚类中心,通过迭代的方式使得样本与各自所属类别的簇中心的距离平方和最小,聚类效果很大程度取决于初始簇中心的选择。
1. 簇间距离度量方法
1.1 最小距离
簇C1和C2的距离取决于两个簇中距离最近的数据样本。
d i s t m i n ( C 1 , C 2 ) = m i n P i ∈ C 1 , P j ∈ C c d i s t ( P i , P j ) dist_{min}(C_1,C_2)=\mathop{min}\limits_{P_i \in C_1,P_j \in C_c}dist(P_i,P_j) distmin(C1,C2)=Pi∈C1,Pj∈Ccmindist(Pi,Pj)
只要两个簇类的间隔不是很小,最小距离算法可以很好的分离非椭圆形状的样本分布,但该算法不能很好的分离簇类间含有噪声的数据集。
1.2 最大距离
簇C1和C2的距离取决于两个簇中距离最远的数据样本。
d i s t m a x ( C 1 , C 2 ) = m a x P i ∈ C 1 , P j ∈ C c d i s t ( P i , P j ) dist_{max}(C_1,C_2)=\mathop{max}\limits_{P_i \in C_1,P_j \in C_c}dist(P_i,P_j) distmax(C1,C2)=Pi∈C1,Pj∈Ccmaxdist(Pi,Pj)
最大距离算法可以很好的分离簇类间含有噪声的数据集,但该算法对球形数据的分离产生偏差。
1.3 平均距离
簇C1和C2的距离等于两个簇类中所有样本对的平均距离。
d i s t a v e r a g e ( C 1 , C 2 ) = 1 ∣ C 1 ∣ . ∣ C 2 ∣ ∑ P i ∈ C 1 , P j ∈ C c d i s t ( P i , P j ) dist_{average}(C_1,C_2)=\frac{1}{|C_1|.|C_2|}\sum\limits_{P_i \in C_1,P_j \in C_c}dist(P_i,P_j) distaverage(C1,C2)=∣C1∣.∣C2∣1Pi∈C1,Pj∈Cc∑dist(Pi,Pj)
1.4 中心法
簇C1和C2的距离等于两个簇中心点的距离。
d i s t m e a n ( C 1 , C 2 ) = d i s t ( M i , M j ) dist_{mean}(C_1,C_2)=dist(M_i,M_j) distmean(C1,C2)=dist(Mi,Mj)
其中M1和M2分别为簇C1和C2的中心点。
1.5 离差平方和
簇类C1和C2的距离等于两个簇类所有样本对距离平方和的平均。
d i s t ( C 1 , C 2 ) = 1 ∣ C 1 ∣ . ∣ C 2 ∣ ∑ P i ∈ C 1 , P j ∈ C c ( d i s t ( P i , P j ) ) 2 dist(C_1,C_2)=\frac{1}{|C_1|.|C_2|}\sum\limits_{P_i \in C_1,P_j \in C_c}(dist(P_i,P_j))^2 dist(C1,C2)=∣C1∣.∣C2∣1Pi∈C1,Pj∈Cc∑(dist(Pi,Pj))2
2. 基于层次的聚类算法
按照分解或者汇聚的原理不同,层次聚类可以分为两种方法:
2.1 凝聚(Agglomerative)
凝聚的方法,也称为自底向上的方法,初始时每个数据样本都被看成是单独的一个簇,然后通过相近的数据样本或簇形成越来越大的簇,直到所有的数据样本都在一个簇中,或者达到某个终止条件为止。
层次凝聚的代表是AGNES(Agglomerative Nesting)算法。
AGNES算法最初将每个数据样本作为一个簇,然后这些簇根据某些准则被一步步地合并。
这是一种单链接方法,其每个簇可以被簇中所有数据样本代表,两个簇间的相似度由这两个不同簇的距离确定(相似度可以定义为距离的倒数)。
算法描述:
输入:数据样本集D,终止条件为簇数目k
输出:达到终止条件规定的k个簇
- 将每个数据样本当成一个初始簇;
- 根据两个簇中距离最近的数据样本找到距离最近的两个簇;
- 合并两个簇,生成新簇的集合;
- 循环step2到step4直到达到定义簇的数目。
2.3 分裂(Divisive)
分裂的方法,也称为自顶向下的方法,它与凝聚层次聚类恰好相反,初始时将所有的数据样本置于一个簇中,然后逐渐细分为更小的簇,直到最终每个数据样本都在单独的一个簇中,或者达到某个终止条件为止。
层次分裂的代表是DIANA(Divisive Analysis)算法。
DIANA算法采用一种自顶向下的策略,首先将所有数据样本置于一个簇中,然后逐渐细分为越来越小的簇,直到每个数据样本自成一簇,或者达到了某个终结条件。
在DIANA方法处理过程中,所有样本初始数据都放在一个簇中。根据一些原则(如簇中最临近数据样本的最大欧式距离),将该簇分裂。簇的分裂过程反复进行,直到最终每个新的簇只包含一个数据样本。
算法描述:
输入:数据样本集D,终止条件为簇数目k
输出:达到终止条件规定的k个簇
- 将所有数据样本整体当成一个初始簇;
- 在所有簇中挑出具有最大直径的簇;
- 找出所挑簇里与其它数据样本平均相异度最大的一个数据样本放入splinter group,剩余的放入old party中;
- 在old party里找出到splinter group中数据样本的最近距离不大于到old party 中数据样本的最近距离的数据样本,并将该数据样本加入splinter group;
- 循环step2到step4直到没有新的old party数据样本分配给splinter group;
- splinter group和old party为被选中的簇分裂成的两个簇,与其他簇一起组成新的簇集合。
3. 基于层次聚类算法的Python实现
AgglomerativeClustering()是scikit-learn提供的层次聚类算法模型,常用形式为:
AgglomerativeClustering(n_clusters=2,affinity='euclidean',memory=None, compute_full_tree='auto', linkage='ward')
参数说明:
- n_clusters:int,指定聚类簇的数量。
- affinity:一个字符串或者可调用对象,用于计算距离。可以为:’euclidean’、’mantattan’、’cosine’、’precomputed’,如果linkage=’ward’,则affinity必须为’euclidean’。
- memory:用于缓存输出的结果,默认为None(不缓存)。
- compute_full_tree:通常当训练到n_clusters后,训练过程就会停止。但是如果compute_full_tree=True,则会继续训练从而生成一颗完整的树。
- linkage:一个字符串,用于指定链接算法。若取值’ward’:单链接single-linkage,采用distmin;若取值’complete’:全链接complete-linkage算法,采用distmax;若取值’average’:均连接average-linkage算法,采用distaverage。
from sklearn import datasets
from sklearn.cluster import AgglomerativeClustering
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
import pandas as pd
iris = datasets.load_iris()
irisdata = iris.data
clustering = AgglomerativeClustering(linkage='ward', n_clusters= 4)
res = clustering.fit(irisdata)
print ("各个簇的样本数目:")
print (pd.Series(clustering.labels_).value_counts())
print ("聚类结果:")
print (confusion_matrix(iris.target, clustering.labels_))
plt.figure()
d0 = irisdata[clustering.labels_ == 0]
plt.plot(d0[:, 0], d0[:, 1], 'r.')
d1 = irisdata[clustering.labels_ == 1]
plt.plot(d1[:, 0], d1[:, 1], 'go')
d2 = irisdata[clustering.labels_ == 2]
plt.plot(d2[:, 0], d2[:, 1], 'b*')
d3 = irisdata[clustering.labels_ == 3]
plt.plot(d3[:, 0], d3[:, 1], 'c.')
plt.xlabel("Sepal.Length")
plt.ylabel("Sepal.Width")
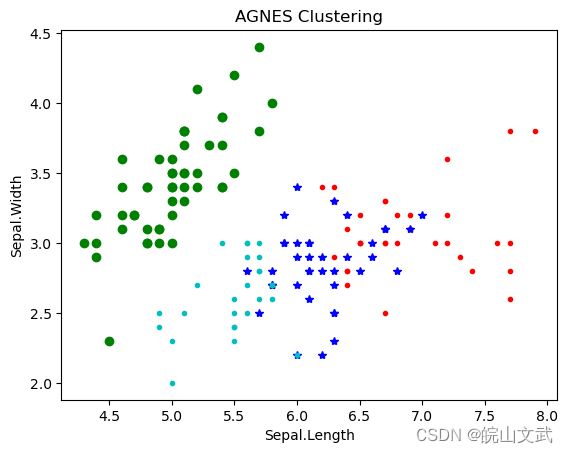
plt.title("AGNES Clustering")
plt.show()各个簇的样本数目:
1 50
2 38
0 36
3 26
dtype: int64
聚类结果:
[[ 0 50 0 0][ 1 0 24 25][35 0 14 1][ 0 0 0 0]]
相关文章:

聚类分析|基于层次的聚类方法及其Python实现
聚类分析|基于层次的聚类方法及其Python实现 0. 基于层次的聚类方法1. 簇间距离度量方法1.1 最小距离1.2 最大距离1.3 平均距离1.4 中心法1.5 离差平方和 2. 基于层次的聚类算法2.1 凝聚(Agglomerative)2.3 分裂(Divisive) 3. 基于…...

前端实现导出xlsx功能
1.安装xlsx插件 npm install xlsx 2.示例 import XLSX from xlsx;// 示例数据 const data [[Name, Age, Country],[Alice, 25, USA],[Bob, 30, Canada],[Charlie, 28, UK] ];// 创建一个 Workbook 对象 const wb XLSX.utils.book_new(); const ws XLSX.utils.aoa_to_sheet…...
算法系列--动态规划--⼦数组、⼦串系列(数组中连续的⼀段)(1)
💕"我们好像在池塘的水底,从一个月亮走向另一个月亮。"💕 作者:Mylvzi 文章主要内容:算法系列–动态规划–⼦数组、⼦串系列(数组中连续的⼀段)(1) 大家好,今天为大家带来的是算法系…...

RESTful架构
RESTful架构中的URI设计与传统的URL设计有一些区别。让我通过具体的例子来解释一下: 传统的URL设计通常将操作和资源混合在一起,例如: 获取所有图书:GET /getBooks获取特定图书:GET /getBookById/{id}创建新图书&…...
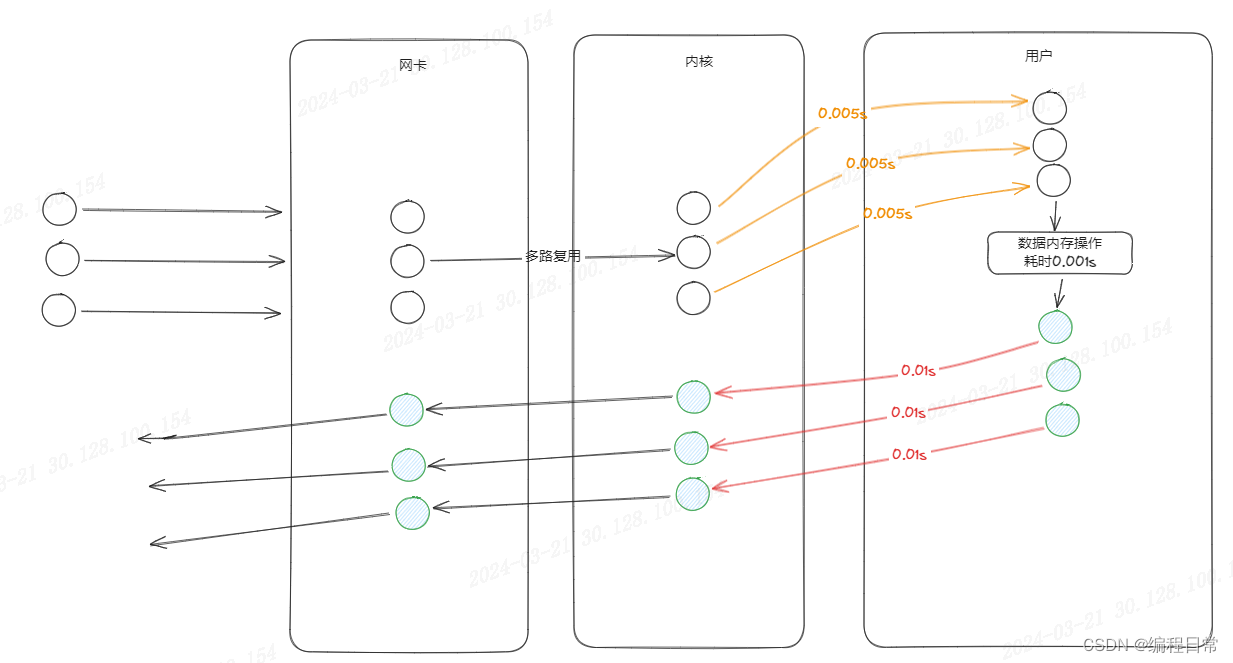
从IO操作与多线程的思考到Redis-6.0
IO操作->线程阻塞->释放CPU资源->多线程技术提升CPU利用率 在没有涉及磁盘操作和网络请求的程序中,通常不会出现线程等待状态。线程等待状态通常是由于线程需要等待某些事件的发生,比如I/O操作完成、网络请求返回等。如果程序只是进行计算或者简…...

MNN介绍、安装和编译
MNN是一个轻量级的深度学习推理框架,由阿里巴巴公司开发。它支持多种硬件平台,包括CPU、GPU和NPU,并提供高效、高性能的深度学习模型推理服务。下面是MNN的安装和编译步骤: 下载MNN源代码 在MNN的GitHub页面(https://g…...

【计算机图形学】AO-Grasp: Articulated Object Grasp Generation
对AO-Grasp: Articulated Object Grasp Generation的简单理解 文章目录 1. 做的事情2. AO-Grasp数据集2.1 抓取参数化和label标准2.2 语义和几何感知的抓取采样 3. AO-Grasp抓取预测3.1 预测抓取点3.2 抓取方向预测 4. 总结 1. 做的事情 引入AO-Grasp,grasp propo…...

「媒体宣传」财经类媒体邀约资源有哪些?-51媒体
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 财经类媒体邀约资源包括但不限于以下几类: 商业杂志和报纸:可以邀请如《财经》、《新财富》、《经济观察报》等主流商业杂志和报纸。这些媒体通常具有较强的品牌影…...

学习资料记录
http://interview.wzcu.com/Golang/%E4%BB%A3%E7%A0%81%E8%80%83%E9%A2%98.html map底层 https://zhuanlan.zhihu.com/p/616979764 go修养 https://www.yuque.com/aceld/golang/ga6pb1#4b19dba5 https://golang.dbwu.tech/performance/map_pre_alloc/ https://juejin.cn/pos…...

数据结构进阶篇 之 【二叉树】详细概念讲解(带你认识何为二叉树及其性质)
有朋自远方来,必先苦其心志,劳其筋骨,饿其体肤,空乏其身,鞭数十,驱之别院 一、二叉树 1、二叉树的概念 1.1 二叉树中组分构成名词概念 1.2 二叉树的结构概念 1.3 特殊的二叉树 2、二叉树的存储结构 …...

vue.js制作学习计划表案例
通俗易懂,完成“学习计划表”用于对学习计划进行管理,包括对学习计划进行添加、删除、修改等操作。 一. 初始页面效果展示 二.添加学习计划页面效果展示 三.修改学习计划完成状态的页面效果展示 四.删除学习计划 当学习计划处于“已完成”状态时&…...

nginx localtion 匹配规则
1、语法规则 语法规则:location[|~|^~*|^~]/uri/{… } 表示精确匹配,这个优先级也是最高的 ^~ 表示 uri 以某个常规字符串开头,理解为匹配 url 路径即可。 nginx 不对 url 做编码,因此请求为 /image/20%/aa,可以被规则^~ /imag…...

Git:分布式版本控制系统
目录 Git的特点和功能常见的功能和对应的命令 Git的特点和功能 Git是一个分布式版本控制系统,用于跟踪和管理项目的代码变更。它是由Linus Torvalds在2005年创建的,旨在管理Linux内核的开发。Git具有以下特点和功能: 分布式版本控制…...

[STL]priority_queue类及反向迭代器的模拟实现
🪐🪐🪐欢迎来到程序员餐厅💫💫💫 今日主菜: priority_queue类及反向迭代器 主厨:邪王真眼 主厨的主页:Chef‘s blog 所属专栏:c大冒险 向着c&…...

vue2 脚手架
安装 文档:https://cli.vuejs.org/zh/ 第一步:全局安装(仅第一次执行) npm install -g vue/cli 或 yarn global add vue/cli 备注:如果出现下载缓慢:请配置npm 淘宝镜像: npm config set regis…...

【OpenStack】OpenStack实战之开篇
目录 那么,OpenStack是什么?云又是什么?关于容器应用程序OpenStack如何适配其中?如何设置它?如何学会使用它?推荐超级课程: Docker快速入门到精通Kubernetes入门到大师通关课AWS云服务快速入门实战我的整个职业生涯到目前为止一直围绕着为离线或隔离网络设计和开发应用程…...

Python实现WebSocket通信
WebSocket是一种在单个TCP连接上进行全双工通信的协议,位于 OSI 模型的应用层。 与传统的HTTP请求-响应模型不同,WebSocket的最大特点就是,服务器可以主动向客户端推送信息,客户端也可以主动向服务器发送信息,实现实时性和互动性…...
MATLAB 自定义生成直线点云(详细介绍) (47)
MATLAB 自定义生成直线点云 (详细介绍)(47) 一、算法介绍二、具体步骤二、算法实现1.代码2.效果一、算法介绍 通过这里的直线生成方法,可以生成模拟直线的点云数据,并通过调整起点、终点、数量和噪声水平等参数来探索不同类型的直线数据。这种方法可以用于测试、验证和开…...
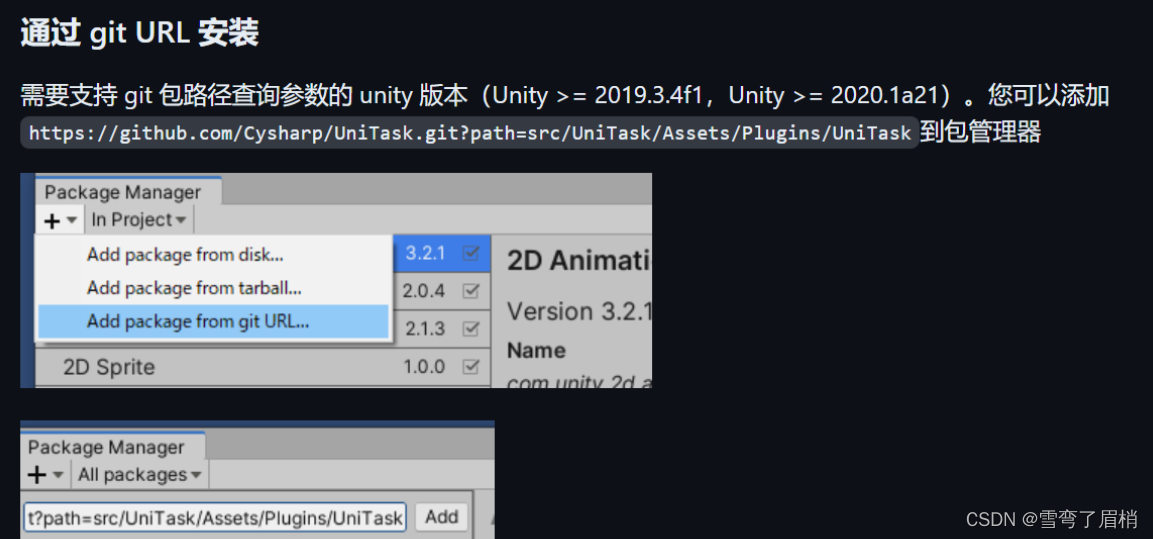
UniTask 异步任务
文章目录 前言一、UniTask是什么?二、使用步骤三、常用的UniTask API和示例1.编写异步方法2.处理异常3.延迟执行4.等待多个UniTask或者一个UniTas完成5.异步加载资源示例6.手动控制UniTask的完成状态7.UniTask.Lazy延迟任务的创建8.后台线程切换Unity主线程9.不要返…...
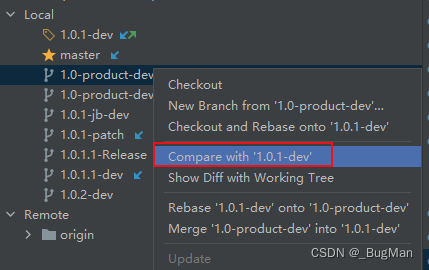
【git分支管理策略】如何高效的管理好代码版本
目录 1.分支管理策略 2.我用的分支管理策略 3.一些常见问题 1.分支管理策略 分支管理策略就是一些经过实践后总结出来的可靠的分支管理的办法,让分支之间能科学合理、高效的进行协作,帮助我们在整个开发流程中合理的管理好代码版本。 目前有两套Git…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
