Laplace变换-3
回忆#常见函数的Laplace变换:
t z − 1 ↦ Γ ( z ) s z t^{z-1} \mapsto \frac{\Gamma(z)}{s^{z}} tz−1↦szΓ(z) (要求 R e ( z ) > 0 \mathrm{Re}(z)>0 Re(z)>0)
e a t ↦ 1 s − a e^{at} \mapsto \frac{1}{s-a} eat↦s−a1
cosh ( a t ) ↦ s s 2 − a 2 \cosh(at) \mapsto \frac{s}{s^2-a^2} cosh(at)↦s2−a2s (要求 s > ∣ R e ( a ) ∣ s > \vert \mathrm{Re}(a) \vert s>∣Re(a)∣) ( cosh ( a t ) = ( 1 / 2 ) ( e a t + e − a t ) \cosh(at)=(1/2)(e^{at}+e^{-at}) cosh(at)=(1/2)(eat+e−at) )
sinh ( a t ) ↦ a s 2 − 2 \sinh(at) \mapsto \frac{a}{s^2-^2} sinh(at)↦s2−2a (要求 s > ∣ I m ( a ) ∣ s > \vert \mathrm{Im}(a) \vert s>∣Im(a)∣) ( sinh ( a t ) = ( 1 / 2 ) ( e a t − e − a t \sinh(at)=(1/2)(e^{at}-e^{-at} sinh(at)=(1/2)(eat−e−at) )
cos ( ω t ) ↦ s s 2 + ω 2 \cos(\omega t) \mapsto \frac{s}{s^2+\omega^2} cos(ωt)↦s2+ω2s (要求 ω ∈ R \omega \in \mathbb{R} ω∈R)
sin ( ω t ) ↦ ω s 2 + ω 2 \sin(\omega t) \mapsto \frac{\omega}{s^2+\omega^2} sin(ωt)↦s2+ω2ω (要求 s > ∣ I m ( ω ) ∣ s > \vert \mathrm{Im}(\omega) \vert s>∣Im(ω)∣) (Euler公式 e i ω = cos ω + i sin ω e^{i\omega}=\cos \omega + i \sin \omega eiω=cosω+isinω)
平移公式:
e a t t z − 1 ↦ Γ ( z ) ( s − a ) z e^{at}t^{z-1} \mapsto \frac{\Gamma(z)}{(s-a)^z} eattz−1↦(s−a)zΓ(z)
e a t cos ω t ↦ s − a ( s − a ) 2 + ω 2 e^{at}\cos \omega t \mapsto \frac{s-a}{(s-a)^2+\omega^2} eatcosωt↦(s−a)2+ω2s−a (要求 ω ∈ R \omega \in \mathbb{R} ω∈R)
e a t sin ω t ↦ ω ( s − a ) 2 + ω 2 e^{at} \sin \omega t \mapsto \frac{\omega}{(s-a)^2+\omega^2} eatsinωt↦(s−a)2+ω2ω (要求 a < s − ∣ I m ( ω ) ∣ a< s - \vert \mathrm{Im}(\omega) \vert a<s−∣Im(ω)∣)
t f ( t ) tf(t) tf(t)的变换公式:
t cos ω t ↦ s 2 − ω 2 ( s 2 + ω 2 ) 2 t \cos \omega t \mapsto \frac{s^2-\omega^2}{(s^2+\omega^2)^2} tcosωt↦(s2+ω2)2s2−ω2 (要求 ω ∈ R \omega \in \mathbb{R} ω∈R)
t sin ω t ↦ 2 s ω ( s 2 + ω 2 ) 2 t\sin \omega t \mapsto \frac{2s\omega}{(s^2+\omega^2)^2} tsinωt↦(s2+ω2)22sω (要求 a < s − ∣ I m ( ω ) ∣ a< s - \vert \mathrm{Im}(\omega) \vert a<s−∣Im(ω)∣)
最后是Heaviside函数的变换公式:
H ( t − t 0 ) ↦ e − t 0 s s H(t-t_0) \mapsto \frac{e^{-t_0s}}{s} H(t−t0)↦se−t0s (要求 t 0 ≥ 0 t_0 \geq 0 t0≥0)
例:解ODE或IVP(初值问题)
- y ′ ′ + 3 y ′ + 2 y = 0 y''+3y'+2y=0 y′′+3y′+2y=0.
- y ′ ′ + 4 y ′ + 4 y = 0 y''+4y'+4y=0 y′′+4y′+4y=0.
- { y ′ ′ − 2 y ′ + 10 y = 0 , y ( 0 ) = 0 , y ′ ( 0 ) = 6. \begin{cases} y''-2y'+10y=0, \\ y(0)=0, y'(0)=6. \end{cases} {y′′−2y′+10y=0,y(0)=0,y′(0)=6.
回忆导函数的变换公式: { [ L y ′ ′ ] ( s ) = s 2 Y ( s ) − s y ( 0 ) − y ′ ( 0 ) , [ L y ′ ] ( s ) = s Y ( s ) − y ( 0 ) . \begin{cases}[Ly''](s)=s^2Y(s)-sy(0)-y'(0), \\ [Ly'](s)=sY(s)-y(0).\end{cases} {[Ly′′](s)=s2Y(s)−sy(0)−y′(0),[Ly′](s)=sY(s)−y(0). 以下写 Y ( s ) = [ L y ] ( s ) Y(s)=[Ly](s) Y(s)=[Ly](s).
-
左边的Laplace变换是 ( s 2 + 3 s + 2 ) Y ( s ) − ( s + 3 ) y ( 0 ) − y ′ ( 0 ) (s^2+3s+2) Y(s) -(s+3)y(0)-y'(0) (s2+3s+2)Y(s)−(s+3)y(0)−y′(0). 特征方程出现了!
解得 Y ( s ) = ( s + 3 ) y ( 0 ) + y ′ ( 0 ) ( s + 1 ) ( s + 2 ) = 2 y ( 0 ) + y ′ ( 0 ) s + 1 − y ( 0 ) + y ′ ( 0 ) s + 2 = C 1 s + 1 + C 2 s + 2 Y(s)= \frac{(s+3)y(0)+y'(0)}{(s+1)(s+2)} = \frac{2y(0)+y'(0)}{s+1} -\frac{y(0)+y'(0)}{s+2} = \frac{C_1}{s+1}+\frac{C_2}{s+2} Y(s)=(s+1)(s+2)(s+3)y(0)+y′(0)=s+12y(0)+y′(0)−s+2y(0)+y′(0)=s+1C1+s+2C2.
查表可知 ( s + a ) − 1 (s+a)^{-1} (s+a)−1是 e − a t e^{-at} e−at的Laplace变换.
所以 y = C 1 e − x + C 2 e − 2 x y=C_1 e^{-x} + C_2 e^{-2x} y=C1e−x+C2e−2x. -
整理得到 ( s 2 + 4 s + 4 ) Y ( s ) = ( s + 4 ) y ( 0 ) + y ′ ( 0 ) (s^2+4s+4)Y(s) = (s+4)y(0)+y'(0) (s2+4s+4)Y(s)=(s+4)y(0)+y′(0). 即 Y ( s ) = ( s + 4 ) y ( 0 ) + y ′ ( 0 ) ( s + 2 ) 2 = y ( 0 ) s + 2 + 2 y ( 0 ) + y ′ ( 0 ) ( s + 2 ) 2 . Y(s) = \frac{(s+4)y(0)+y'(0)}{(s+2)^2} = \frac{y(0)}{s+2}+\frac{2y(0)+y'(0)}{(s+2)^2}. Y(s)=(s+2)2(s+4)y(0)+y′(0)=s+2y(0)+(s+2)22y(0)+y′(0).
查表,知 ( s + 2 ) − 1 , ( s + 2 ) − 2 (s+2)^{-1}, (s+2)^{-2} (s+2)−1,(s+2)−2分别是 e − 2 x , x e − 2 x e^{-2x}, xe^{-2x} e−2x,xe−2x的Laplace变换.
所以 y = C 1 e − 2 x + C 2 x e − 2 x y=C_1 e^{-2x} + C_2xe^{-2x} y=C1e−2x+C2xe−2x. -
求出 Y ( s ) = 2 × 3 ( s − 1 ) 2 + 3 2 Y(s) = \frac{2\times 3}{(s-1)^2+3^2} Y(s)=(s−1)2+322×3, 故 y = 2 e x ⋅ sin ( 3 x ) y=2e^x\cdot \sin(3x) y=2ex⋅sin(3x).
注:如果初值条件不是在 x = 0 x=0 x=0处给出,则用Laplace变换解此种IVP需要更多的技巧.
- 考虑 { y ′ ′ − 2 y ′ + y = ( x − 1 ) e x , y ( 1 ) = y ′ ( 1 ) = 1. \begin{cases} y''-2y'+y=(x-1)e^x, \\ y(1)=y'(1)=1. \end{cases} {y′′−2y′+y=(x−1)ex,y(1)=y′(1)=1.
特解是 y = ( 6 − e 6 e + x 2 ) e x + 1 6 x 3 e x − 1 2 x 2 e x y=(\frac{6-e}{6e}+\frac{x}{2})e^x+\frac{1}{6}x^3e^x-\frac{1}{2}x^2e^x y=(6e6−e+2x)ex+61x3ex−21x2ex.
注意此处的初值条件不是在自变量取0时给出,不能直接两边应用Laplace变换。 这个IVP可以这样求解:
设函数 f ( t ) f(t) f(t)满足 f ( x − 1 ) = y ( x ) f(x-1)=y(x) f(x−1)=y(x). 注意 d n d x n y ( x ) = d n d t n f ( t ) \frac{d^n}{dx^n} y(x) = \frac{d^n}{dt^n} f(t) dxndny(x)=dtndnf(t), 所以原ODE化为 f ′ ′ ( t ) − 2 f ′ ( t ) + f ( t ) = t e t e . (1) f''(t)-2f'(t)+f(t)=te^te. \tag{1} f′′(t)−2f′(t)+f(t)=tete.(1)而初值条件变为 f ( 0 ) = f ′ ( 0 ) = 1 f(0)=f'(0)=1 f(0)=f′(0)=1.
对 ( 1 ) (1) (1)两边应用Laplace变换:写 F ( s ) = [ L f ] ( s ) F(s)=[Lf](s) F(s)=[Lf](s), 应用初值条件,有 ( s − 1 ) 2 F ( s ) − s + 1 = e ( s − 1 ) − 2 . (s-1)^2 F(s) - s+1 = e(s-1)^{-2}. (s−1)2F(s)−s+1=e(s−1)−2.由此可得 F ( s ) = 1 s − 1 + e Γ ( 4 ) Γ ( 4 ) ( s − 1 ) 4 . F(s) = \frac{1}{s-1}+\frac{e}{\Gamma(4)}\frac{\Gamma(4)}{(s-1)^4}. F(s)=s−11+Γ(4)e(s−1)4Γ(4).
查表可知 f ( t ) = ( e / 6 ) t 3 e t + e t f(t)=(e/6)t^3e^t + e^t f(t)=(e/6)t3et+et. 所以原IVP的特解是 y ( x ) = f ( x − 1 ) = ( x − 1 ) 3 6 e x + e x − 1 . y(x)=f(x-1)= \frac{(x-1)^3}{6}e^x+e^{x-1}. y(x)=f(x−1)=6(x−1)3ex+ex−1.
这与一开始给出的特解相同。
注意:上述求解过程虽然给出了答案,但如果严格论证,需要用到平移性质2, 此处从略。
注:如果取 s = 2 π i ω ( ω s=2\pi i \omega (\omega s=2πiω(ω是圆频率 ) ) ), 则Laplace变换变成经典的Fourier变换: f ( t ) ↦ f ^ ( ω ) = ∫ 0 ∞ e − 2 π i ω ⋅ t f ( t ) d t . f(t) \mapsto \hat{f}(\omega) = \int_0^\infty e^{-2\pi i \omega \cdot t}f(t) dt. f(t)↦f^(ω)=∫0∞e−2πiω⋅tf(t)dt.
特别,Laplace变换与Fourier变换,都能够把函数的卷积,变换成乘法:函数 f , g f, g f,g的卷积(convolution)定义为 ( f ∗ g ) ( t ) = ∫ − ∞ ∞ f ( τ ) g ( t − τ ) d τ . (f*g)(t)=\int_{-\infty}^{\infty} f(\tau)g(t-\tau)d\tau. (f∗g)(t)=∫−∞∞f(τ)g(t−τ)dτ.
不难证明 f ∗ g = g ∗ f f*g = g*f f∗g=g∗f. 而 [ L ( f ∗ g ) ( t ) ] ( s ) = [ L f ] ( s ) ⋅ [ L g ] ( s ) , ( f ∗ g ) ( t ) ^ = f ^ ( ω ) ⋅ g ^ ( ω ) . [L(f*g)(t)](s)=[Lf](s)\cdot [Lg](s), \quad (f*g)(t)\hat{} = \hat{f}(\omega)\cdot \hat{g}(\omega). [L(f∗g)(t)](s)=[Lf](s)⋅[Lg](s),(f∗g)(t)^=f^(ω)⋅g^(ω).
相关文章:

Laplace变换-3
回忆#常见函数的Laplace变换: t z − 1 ↦ Γ ( z ) s z t^{z-1} \mapsto \frac{\Gamma(z)}{s^{z}} tz−1↦szΓ(z) (要求 R e ( z ) > 0 \mathrm{Re}(z)>0 Re(z)>0) e a t ↦ 1 s − a e^{at} \mapsto \frac{1}{s-a} eat↦s−a1…...
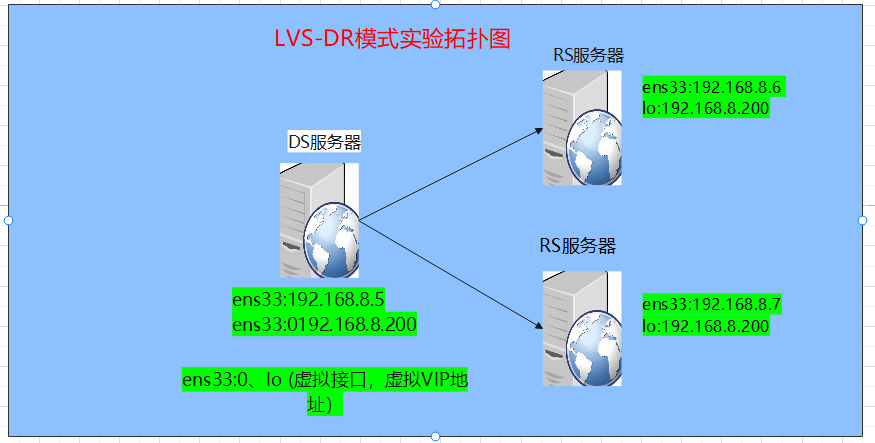
LVS负载均衡-DR模式配置
LVS:Linux virtual server ,即Linux虚拟服务器 LVS自身是一个负载均衡器(Director),不直接处理请求,而是将请求转发至位于它后端的真实服务器real server上。 LVS是四层(传输层 tcp/udp)负载均衡…...
【unity】如何汉化unity Hub
相信大家下载安装unity后看着满操作栏的英文,英文不好的小伙伴们会一头雾水。但是没关系你要记住你要怎么高速运转的机器进入中国,请记住我给出的原理,不懂不代表不会用啊。现在我们就来把编译器给进行汉化。 第一步:我们打开Uni…...

【算法】KMP-快速文本匹配
文章目录 一、KMP算法说明二、详细实现1. next数组定义2. 使用next加速匹配3. next数组如何快速生成4. 时间复杂度O(mn)的证明a) next生成的时间复杂度b) 匹配过程时间复杂度 三、例题1. [leetcode#572](https://leetcode.cn/problems/subtree-of-another-tree/description/)2.…...

多维数组和交错数组笔记
1.) 关于数据的几个概念: Rank,即数组的维数,其值是数组类型的方括号之间逗号个数加上1。 Demo:利用一维数组显示斐波那契数列F(n) F(n-1) F(n-2) (n >2 ),每行显示5项,20项. static void Main(string[] args){int[] F n…...

Python(django)之单一接口展示功能前端开发
1、代码 建立apis_manage.html 代码如下: <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><title>测试平台</title> </head> <body role"document"> <nav c…...

【大模型】非常好用的大语言模型推理框架 bigdl-llm,现改名为 ipex-llm
非常好用的大语言模型推理框架 bigdl-llm,现改名为 ipex-llm bigdl-llmgithub地址环境安装依赖下载测试模型加载和优化预训练模型使用优化后的模型构建一个聊天应用 bigdl-llm IPEX-LLM is a PyTorch library for running LLM on Intel CPU and GPU (e.g., local P…...

Kubernetes示例yaml:3. service-statefulset.yaml
service-statefulset.yaml 示例 apiVersion: apps/v1 kind: statefulset metadata:...... spec:......volumeMounts:- name: pvcmountPath: /var/lib/arangodb3VolumeClaimTemplates:- metadata:name: pvcspec:accessModes: [ "ReadWriteOnce" ]storangeClassName: …...

Windows平台cmake编译QT源码库,使用VScode开发QT
不愿意安装庞大的QT开发IDE,可以编译QT源码库。 下载源码可以用国内镜像,如清华大学的:Index of /qt/archive/qt/ | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 我用的是 6.5.3,进去之后,不要下载整个源…...

腾讯云轻量8核16G18M服务器多少钱一年?
腾讯云轻量8核16G18M服务器多少钱一年?优惠价格4224元15个月,买一年送3个月。配置为轻量应用服务器、16核32G28M、28M带宽、6000GB月流量、上海/广州/北京、380GB SSD云硬盘。 腾讯云服务器有两个活动,一个是官方的主会场入口,还…...
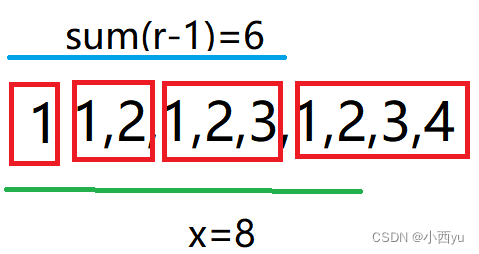
二分练习题——123
123 二分等差数列求和前缀和数组 题目分析 连续一段的和我们想到了前缀和,但是这里的l和r的范围为1e12,明显不能用O(n)的时间复杂度去求前缀和。那么我们开始观察序列的特点,可以按照等差数列对序列进行分块。如上图,在求前10个…...
淘宝详情数据采集(商品上货,数据分析,属性详情,价格监控),海量数据值得get
淘宝详情数据采集涉及多个环节,包括商品上货、数据分析、属性详情以及价格监控等。在采集这些数据时,尤其是面对海量数据时,需要采取有效的方法和技术来确保数据的准确性和完整性。以下是一些关于淘宝详情数据采集的建议: 请求示…...
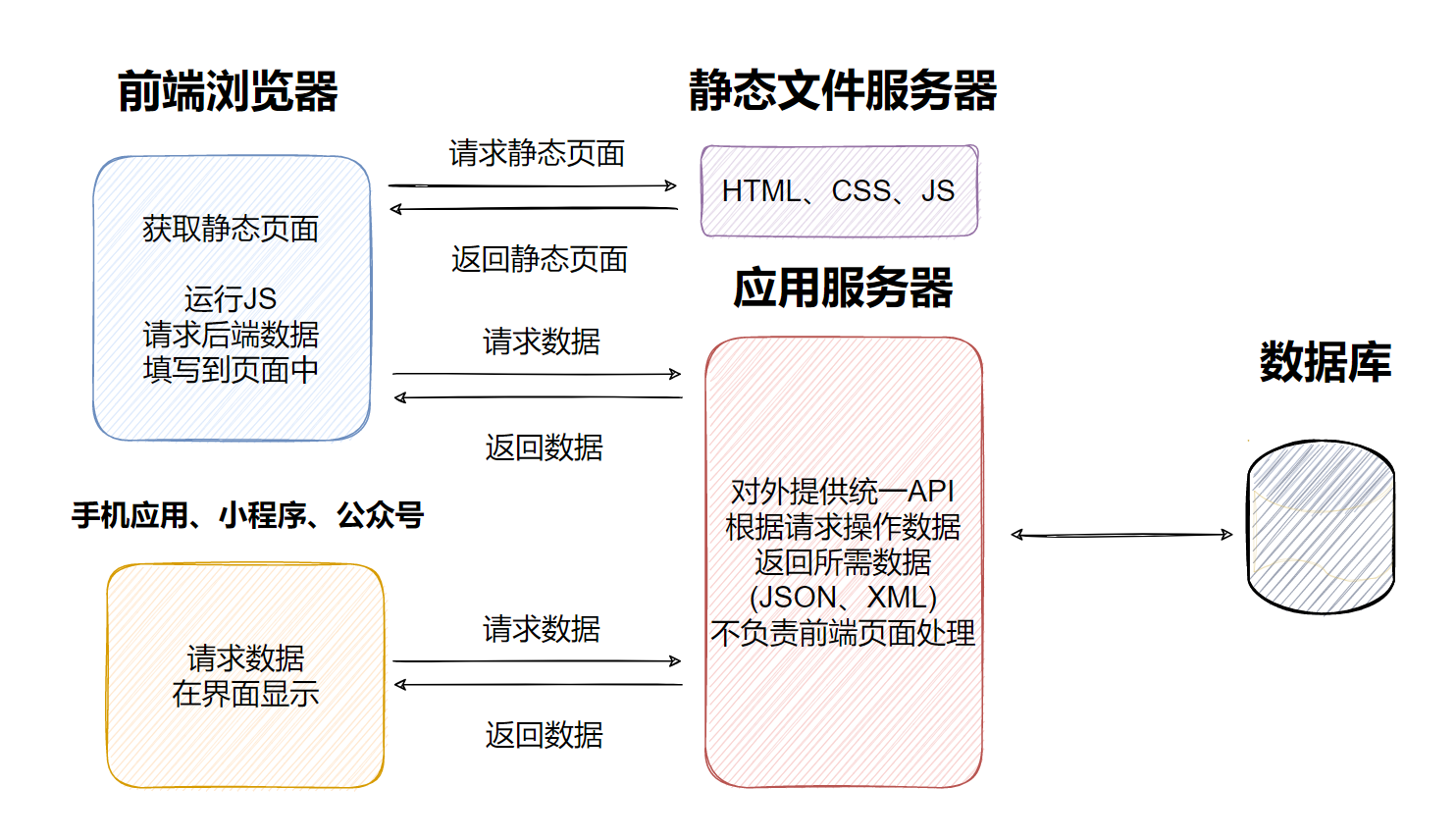
Django之Web应用架构模式
一、Web应用架构模式 在开发Web应用中,有两种模式 1.1、前后端不分离 在前后端不分离的应用模式中,前端页面看到的效果都是由后端控制,由后端渲染页面或重定向,也就是后端需要控制前端的展示。前端与后端的耦合度很高 1.2、前后端分离 在前后端分离的应用模式中,后端仅返…...

GPT提示词分享 —— 口播脚本
可用于撰写视频、直播、播客、分镜头和其他口语内容的脚本。 提示词👇 请以人的口吻,采用缩略语、成语、过渡短语、感叹词、悬垂修饰语和口语化语言,避免重复短语和不自然的句子结构,撰写一篇关于 [主题] 的文章。 GPT3.5&#…...
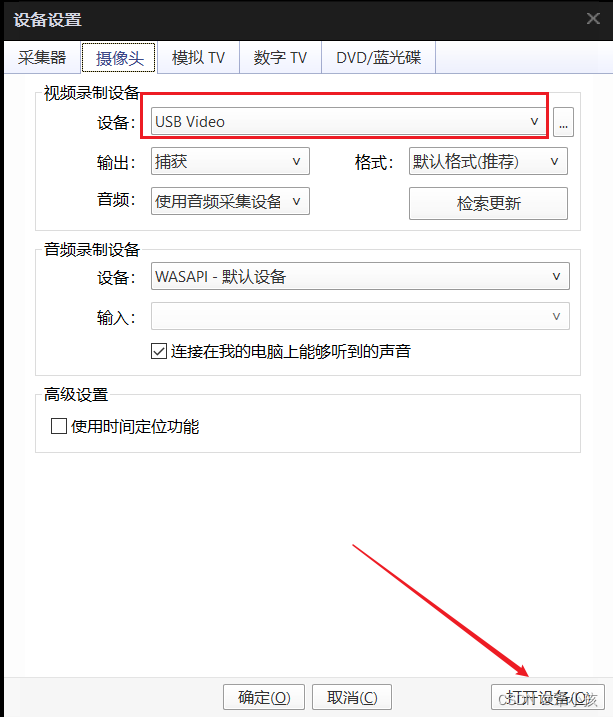
笔记本作为其他主机显示屏(HDMI采集器)
前言: 我打算打笔记本作为显示屏来用,连上工控机,这不是贼方便吗 操作: 一、必需品 HDMI采集器一个 可以去绿联买一个,便宜的就行,我的大概就长这样 win10下载 PotPlayer 软件 下载链接:h…...
02.percona Toolkit工具pt-archiver命令实践
1.命令作用 Percona Toolkit有的32个命令,可以分为7大类 工具类别 工具命令 工具作用 备注 开发类 pt-duplicate-key-checker 列出并删除重复的索引和外键 pt-online-schema-change 在线修改表结构 pt-query-advisor 分析查询语句,并给出建议&#x…...

【天狼启航者】研究计划
“造车”,预计在4月中旬展开(嵌入式蓝桥杯比赛结束后),这里先计划一下,不断更新。 基本要求: 使用STM32F407系列芯片,使用FreeRTOS系统。 驱动程序必须要有强大的可移植性、模块化、低耦合、简…...
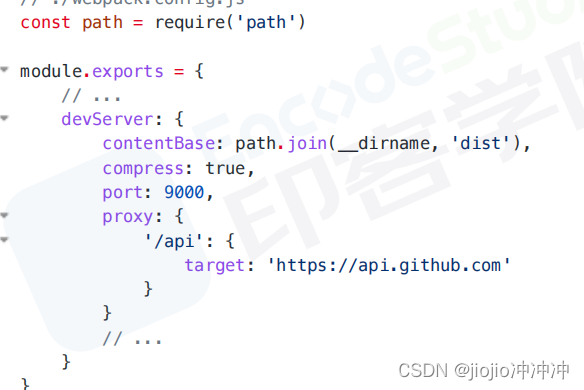
面试题 之 webpack
1.说说你对webpack理解?解决什么问题? Webpack 是实现前端项目的模块化,用于现代 JavaScript 应用程序的静态模块打包工具,被webpack 直接引用的资源打包进 bunde.js的资源,当webpack 处理应用程序时,它会在内部构建一…...

【机器学习之旅】概念启程、步骤前行、分类掌握与实践落地
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...
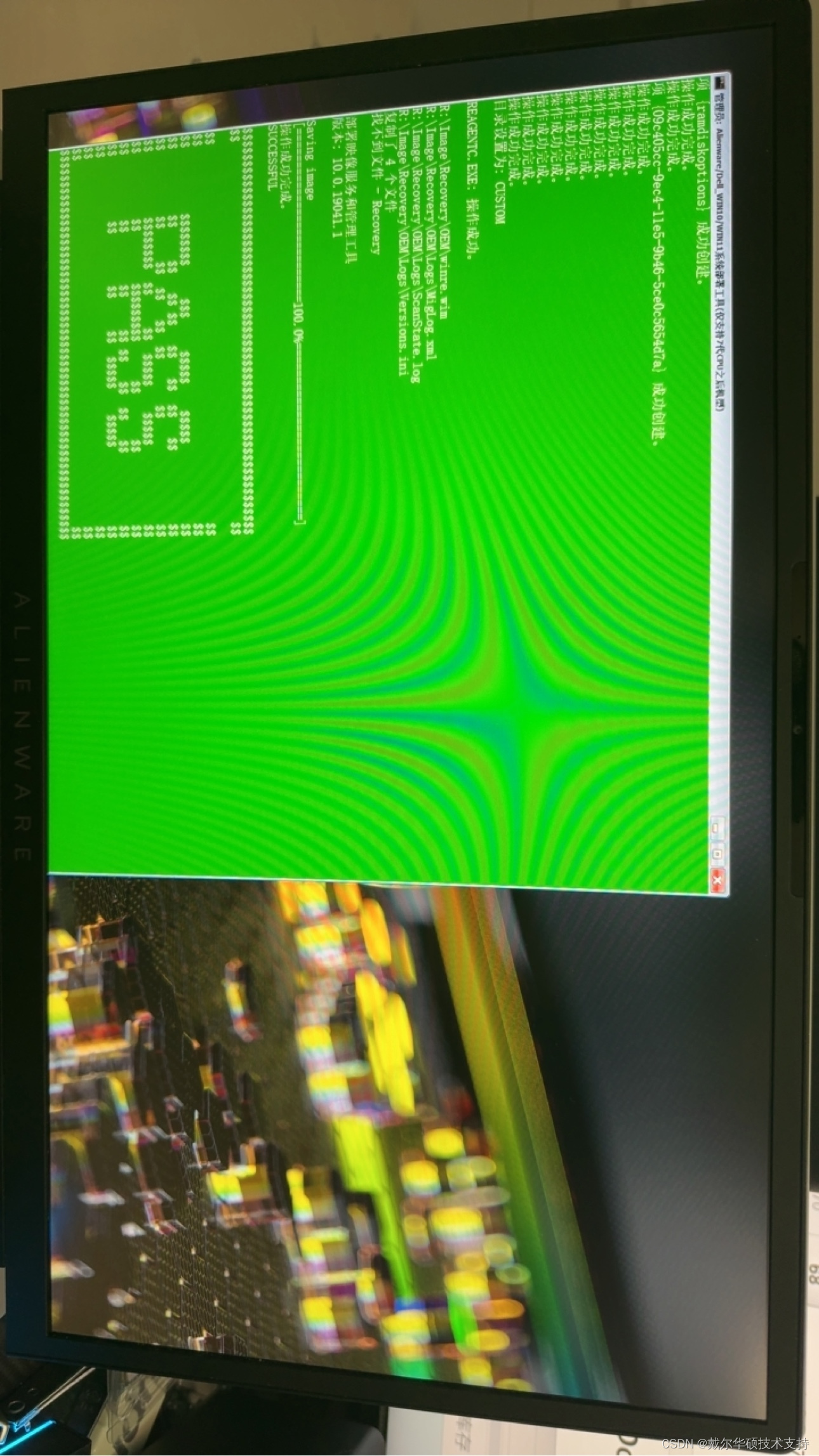
外星人m18R2国行中文版原厂预装23H2原装Win11系统恢复带F12恢复重置
戴尔外星人m18R2国行中文版原厂预装23H2系统恢复安装 远程恢复安装:https://pan.baidu.com/s/166gtt2okmMmuPUL1Fo3Gpg?pwdm64f 提取码:m64f 1.自带原厂预装系统各驱动,主题,Logo,Office带所有Alienware主题壁纸、Alienware软件驱动 2.带…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
