基于ATX自动化测试解决方案
在整车开发中,诊断功能实现后需要进行测试验证。测试验证主要分为两个方面:诊断协议层测试和诊断功能测试。诊断协议层测试:需要对服务层服务定义、传输层相关时间参数进行测试验证;诊断功能测试:需要对各诊断功能项,如DID具体数值校验、Coding配置检查等进行功能验证。而这样的测试验证在前期开发中是一项非常耗费人力和时间周期的工作。针对测试管理,ASAM制定了ATX(Automotive Test Exchange Format)标准,用于在不同的测试系统之间交换测试数据。

一 Softing Q-Automation 软件
Softing Q-Automation软件,基于ATX标准,支持以上测试需求。它结合了ODX诊断数据库以及OTX测试序列,并且可以实现协议层全自动生成测试序列和诊断功能测试,以及Excel测试表格的填写,从而实现了半自动化测试需求。此外,它还可缩短用户的测试周期,让原本数月的工作量在几周内完成。同时,因为ODX/OTX标准化工具支持多种测试硬件,所以通过使用它,用户还可以大大避免测试软件的兼容性问题。
二 Q-Automation 功能模块介绍
| Test Specification 测试规范
测试规范:主要用于定义测试序列中的测试变量、判定机制和测试操作等。
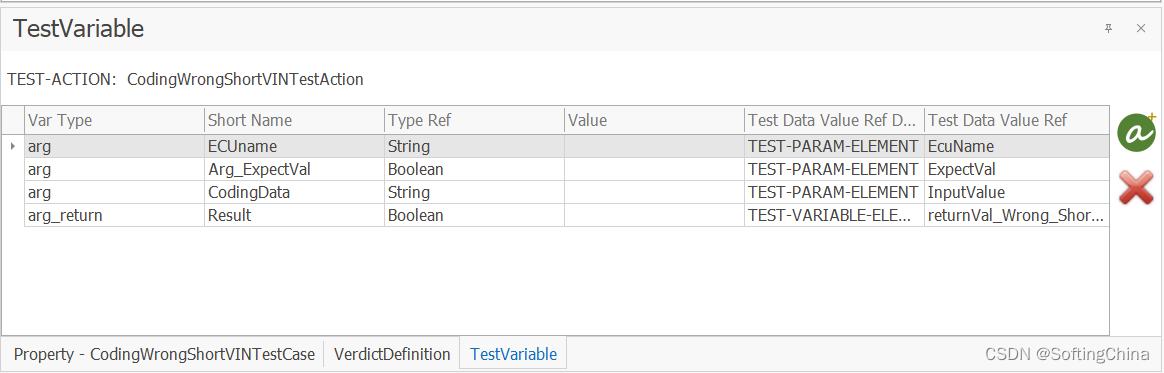
| Test Preparation 测试准备
测试准备:用于定义测试数据和加载测试执行脚本。Q-Automation支持加载Excel测试模板,关联测试用脚本(OTX/Python/.NET等)和关联测试用ODX数据库等功能。
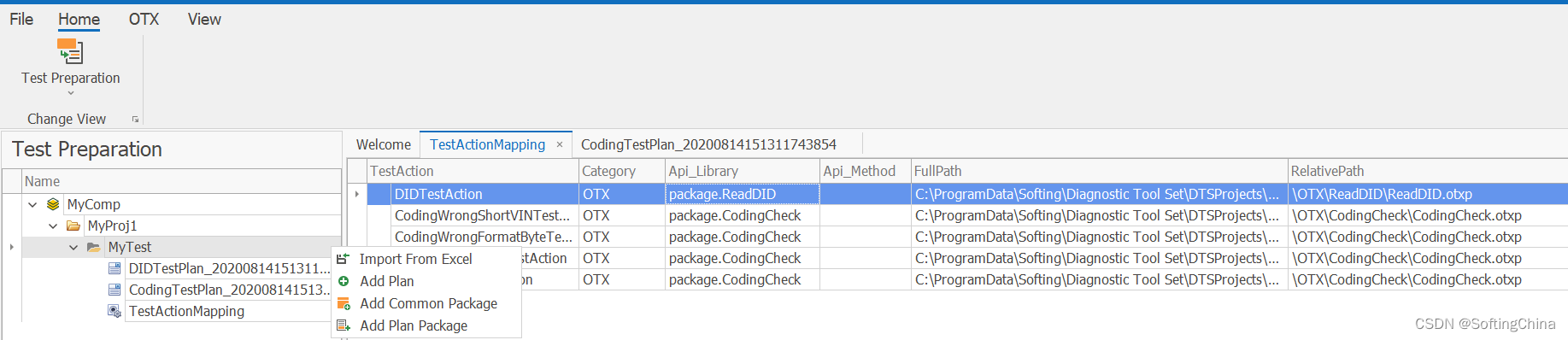
| Test Execution 测试执行
测试执行:测试用例执行模块。在外部测试设备连接无误情况下,一键进行用例测试。执行结果与测试Log实时显示。

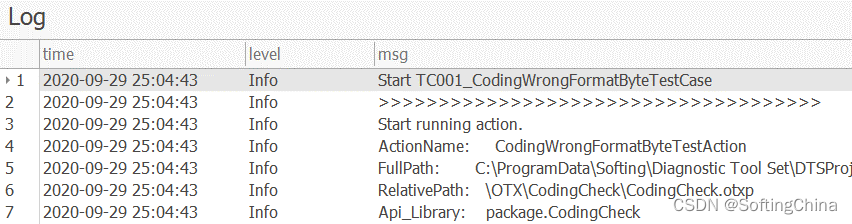
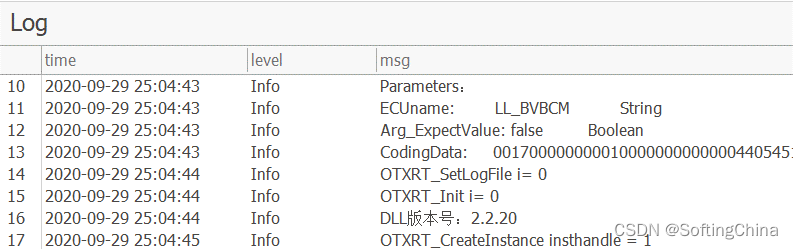
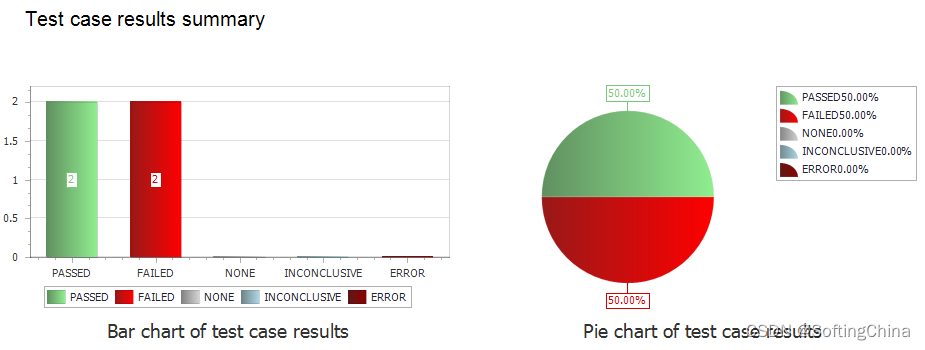
| Test Report 测试报告
测试报告:测试结果自动生成测试报告,支持对测试结果进行预览,同时也可针对具体测试项进行测试情况具体校验。测试报告支持以PDF/HTML格式导出。

三 Q-Automation 功能优势
| 协议测试全自动
Q-Automation基于ASAM协议标准开发,并无缝衔接ODX/OTX标准。Q-Automation可支持从ODX数据库中直接获取诊断数据,例如通讯参数、时序、填充字节、服务列表和正负响应等。它还可自动生成OTX测试用例并对协议进行测试,从而保证了协议测试用例的完整性。

| 功能测试半自动
因为各功能项和测试流程的差异,所以在以往的测试工作中,诊断功能测试是一项繁琐且耗时的工作。对此,Q-Automation通过制定Excel测试模板的形式,简化了用户的工作......
请点击此处,查看剩余30%精彩内容!
| 往期回顾
▶ 基于ODX/OTX诊断的整车扫描
▶ 基于OBD系统的量产车评估测试(PVE)

相关文章:

基于ATX自动化测试解决方案
在整车开发中,诊断功能实现后需要进行测试验证。测试验证主要分为两个方面:诊断协议层测试和诊断功能测试。诊断协议层测试:需要对服务层服务定义、传输层相关时间参数进行测试验证;诊断功能测试:需要对各诊断功能项&a…...
Qt学习5-Qt Creator文件操作(哔站视频学习记录)
实现文件编辑器代码 目录 一、代码要点 二、重点函数 1、conncet 2、getOpenFileName 3、getSaveFileName 4、读取文件到textEdit 5、textEdit保存到文件 三、全部代码 mainwindow.h mainwindow.cpp 一、代码要点 MainWindow的菜单栏实现;connect函数连接…...

LeetCode15三数之和 容易理解版本
题目: 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三…...

Spring Boot 3.0系列【11】核心特性篇之国际化
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot版本3.0.3 源码地址:https://gitee.com/pearl-organization/study-spring-boot3 文章目录 前言基础知识国际化简介浏览器语言LocaleMessageSourceMessageSourcePropertiesLocaleResolver案例演示案例一:后台消息国…...

每日学术速递3.7
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.Dropout Reduces Underfitting 标题:Dropout 减少欠拟合 作者:Zhuang Liu, Zhiqiu Xu, Joseph Jin, Zhiqiang Shen, Trevor Darrel 文章链接:h…...
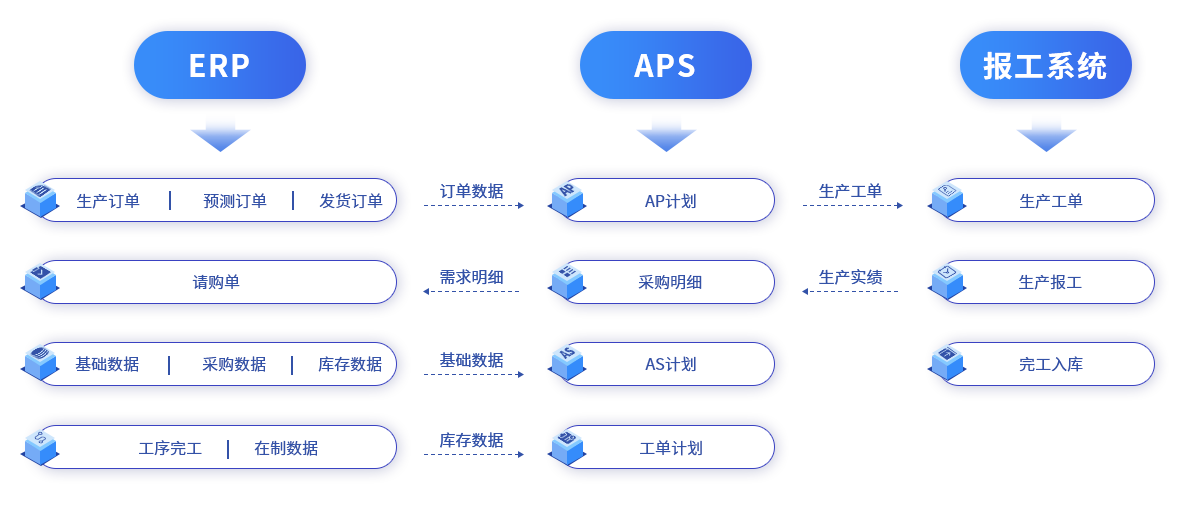
灯具照明行业MES系统,助力企业实现数字化转型
灯具照明行业在制造领域,是典型的高科技离散生产制造模式,大部分企业都设置:电源组件、光源组件、或光电一体组件 ,工艺以SMT、DIP等。 灯罩主要采用吸塑工艺及模具加工;其它金属的面盖、灯体、灯盒基本都是采用压铸、…...

超实用!JavaScript修改CSS变量,达到动态修改样式的目的
在网页开发中,我们通常使用CSS来设置网页的样式。但是,在开发过程中,有时候我们需要根据不同的条件来动态修改样式,这时候就需要使用JavaScript来实现。 在CSS中,有一种变量的概念,可以使用变量来定义颜色…...
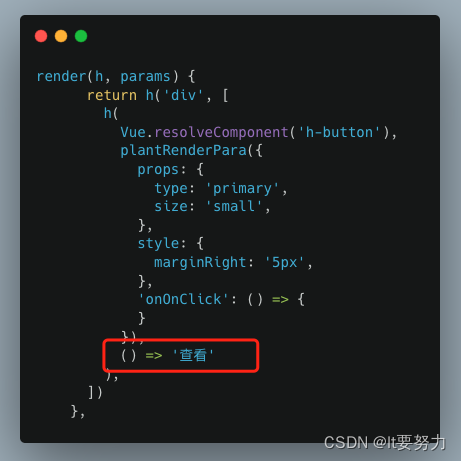
解决Vue3 默认槽的非函数值 - Non-function value encountered for default slot 的警告
解决警告⚠️:[Vue warn]: Non-function value encountered for default slot. Prefer function slots for better performance. h函数的第三个参数加上箭头函数 原因分析: 一般 第三个参数如果不是默认插槽的话 就是当作children传下去,…...
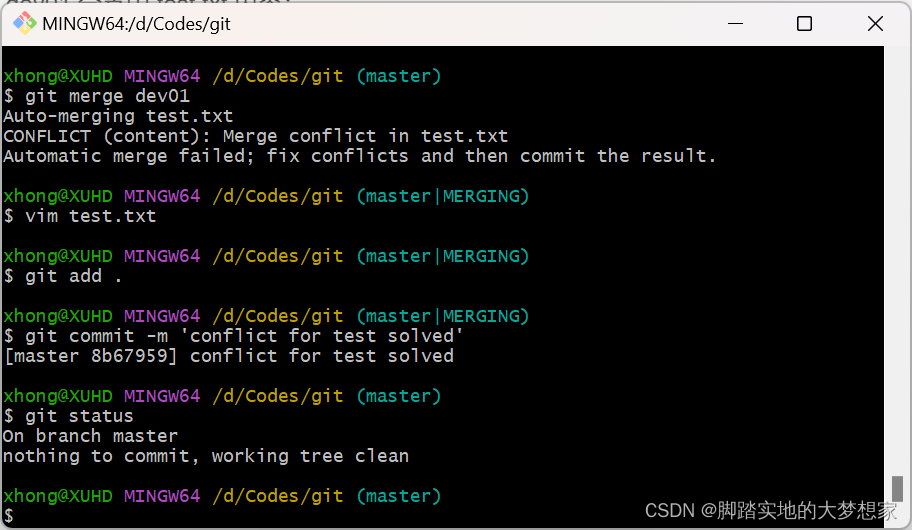
【Git】P2 分支(创建分支,合并分支,分支冲突,分支分类)
分支分支的概念2077 与 分支git - 分支分支语句查看与创建分支切换与删除分支合并分支分支冲突分支分类分支的概念 什么是分支? 2077 与 分支 我最喜欢的游戏就是 赛博朋克2077,美国末日 和 GTA,下图是2077的存档。 存档非常多的原因是因为…...

2023年全国最新交安安全员精选真题及答案14
百分百题库提供交安安全员考试试题、交安安全员考试预测题、交安安全员考试真题、交安安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 41.事故隐患泛指生产系统中可导致事故发生的() A.人的不…...

Air101|Air103|Air105|Air780E|ESP32C3|ESP32S3|Air32F103开发板:概述及PinOut
内容均引自合宙官方wiki,详细内容请参考: :LuatOS 文档 。 1、合宙Air101(芯片及开发板) 合宙Air101是一款QFN32 封装,4mm x 4mm 大小的mcu。通用串口波特率,设置波特率为921600。 固件编译可…...

【代码随想录训练营】【Day35】第八章|贪心算法|860.柠檬水找零|406.根据身高重建队列|452. 用最少数量的箭引爆气球
柠檬水找零 题目详细:LeetCode.860 一道非常简单的模拟题,根据题目要求编写程序即可: Java解法(模拟): class Solution {public boolean lemonadeChange(int[] bills) {int money_5 0, money_10 0;fo…...
)
嵌入式C基础知识(23)
常用C/C代码规范头文件的保护所有的头文件都应该使用#define来避免多次引用,符号格式为:<PROJECT>_<PATH>_<FILE>_H_例如头文件:foo/src/bar/baz.h#ifndef FOO_BAR_BAZ_H_#define FOO_BAR_BAZ_H_...#endif // FOO_BAR_BAZ_…...

一文掌握组织项目等级划分维度,标准和实例
当你遇到多项目怎么管?遇到项目之间的冲突怎么解决?很多公司没有项目优先级的划分,会对企业造成很多严重的问题。首先,会造成不合理的资源分配:缺少项目优先级的情况下,很难确定哪些项目是最重要的…...
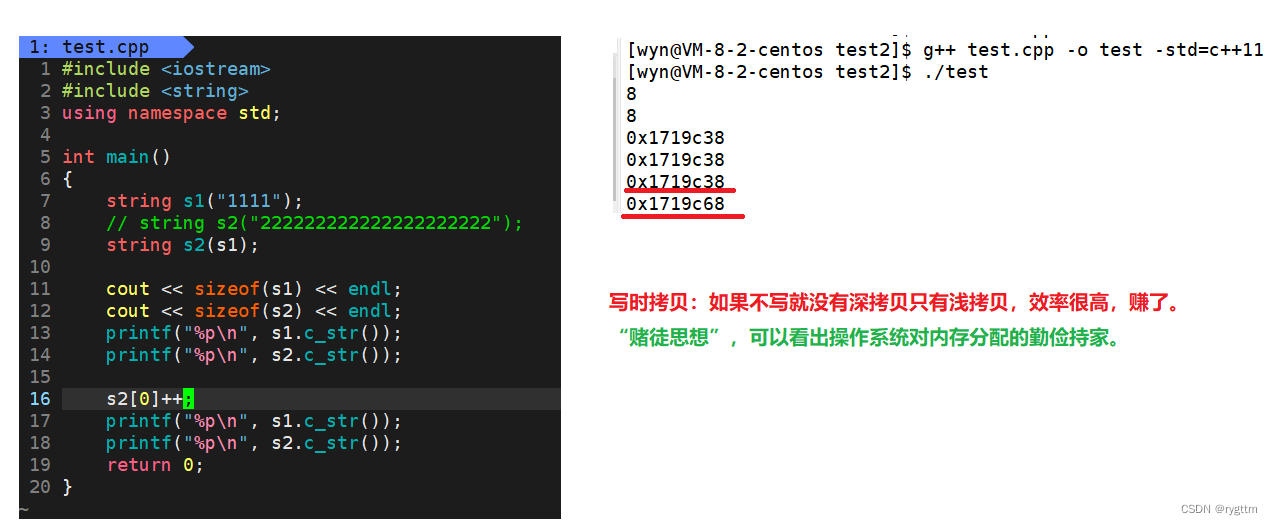
【C++】list的使用和基本迭代器框架的实现 vs和g++下string结构的说明
真正的成熟应该并不是追求完美,而是直面自己的缺憾,这才是生活的本质。 文章目录一、初见list1.list的迭代器失效和基本使用2.list的operations操作接口(看起来挺不错的接口,但可惜不怎么实用)3.vector和list的排序性能…...
基于深度学习的轴承寿命预测实践,开发CNN、融合LSTM/GRU/ATTENTION
关于轴承相关的项目之前做的大都是故障识别诊断类型的,少有涉及回归预测的,周末的时候宅家发现一个轴承寿命加速实验的数据集就想着拿来做一下寿命预测。首先看下数据集如下:直接百度即可搜到,这里就不再赘述了。Learning_set为训…...
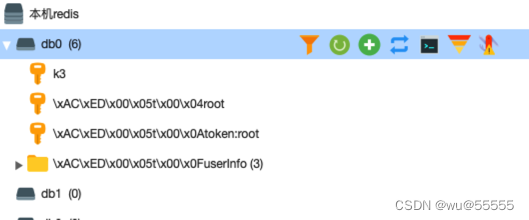
redis进阶:mysql,redis双写一致性,数据库更新后再删除缓存就够了吗?
0. 引言 最近线上的一个状态修改功能出现了问题,一开始是运营找了过来,运营告知某条数据的状态已经开启了的,但是实际使用起来还是没有生效,于是拿到这个问题后,首先就去数据库查了这条数据,发现确实如他所…...
RTOS中互斥量的原理以及应用
互斥量的原理 RTOS中的互斥量是一种同步机制,用于保护共享资源,防止多个任务同时访问该资源,从而避免数据竞争和不一致性。 互斥量的原理是通过对共享资源进行加锁和解锁操作来实现的。 在RTOS中,互斥量通常是一个数据结构&…...
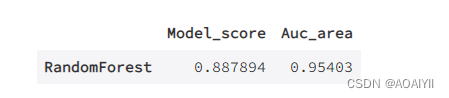
数据分析:基于随机森林(RFC)对酒店预订分析预测
数据分析:基于随机森林(RFC)对酒店预订分析预测 作者:AOAIYI 作者简介:Python领域新星作者、多项比赛获奖者:AOAIYI首页 😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞…...
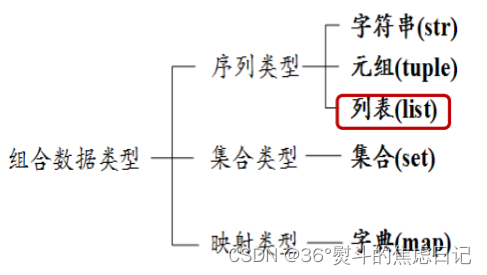
【python】序列(列表、元组)、字典、集合的初步认识
一、序列 序列类型(sequence):一组有序的数据集,特点是数据之间存在先后关系,通过序号访问 序列包含以下三种类型: 1.字符串(str)不可修改 2.列表(list)可修改 3.元组(t…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...
