leetcode热题100.跳跃游戏2
Problem: 45. 跳跃游戏 II
文章目录
- 题目
- 思路
- 复杂度
- Code
题目
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
$0 <= j <= nums[i] $
i + j < n i + j < n i+j<n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
思路
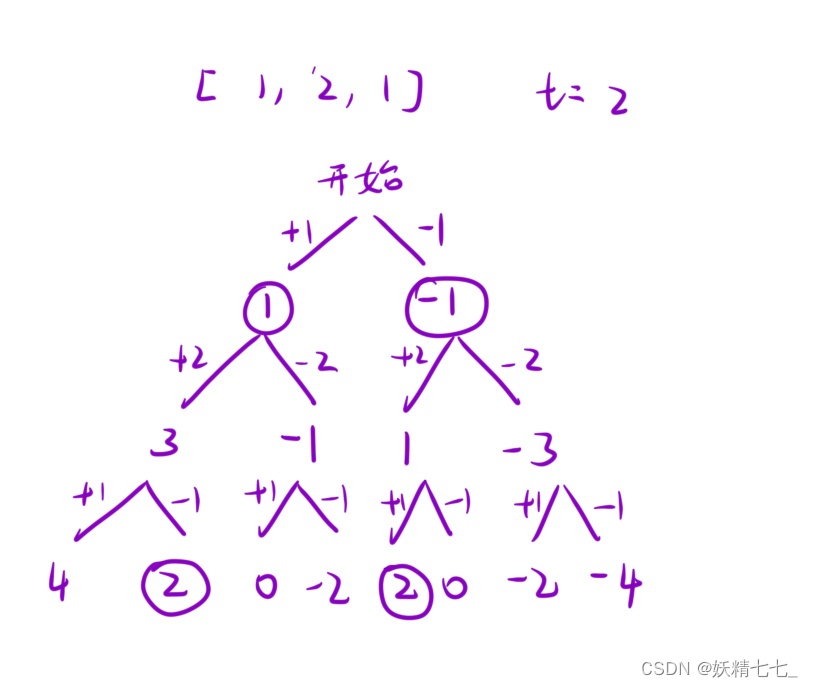
我们思考一种朴素的解法,就是从后往前遍历遍历所有点x,在这层循环中再从左往右遍历所有点,看看哪个点最先能到达x,这个点就是我们的下一个要达到的点,然后我们再从左往右寻找能到达这个点的点就ok
class Solution {public int jump(int[] nums) {int position = nums.length - 1;int steps = 0;while (position > 0) {for (int i = 0; i < position; i++) {if (i + nums[i] >= position) {position = i;steps++;break;}}}return steps;}
}
我们观察下每次跳跃的规律,就拿 [ 2 , 3 , 1 , 2 , 4 , 2 , 3 ] [2,3,1,2,4,2,3] [2,3,1,2,4,2,3] 来说,
- 对于位置0而言,他可以跳到位置1,2上;
- 对于位置1而言,他可以跳到2,3,4这些位置上;
- 对于位置2而言,他可以跳到位置4上;
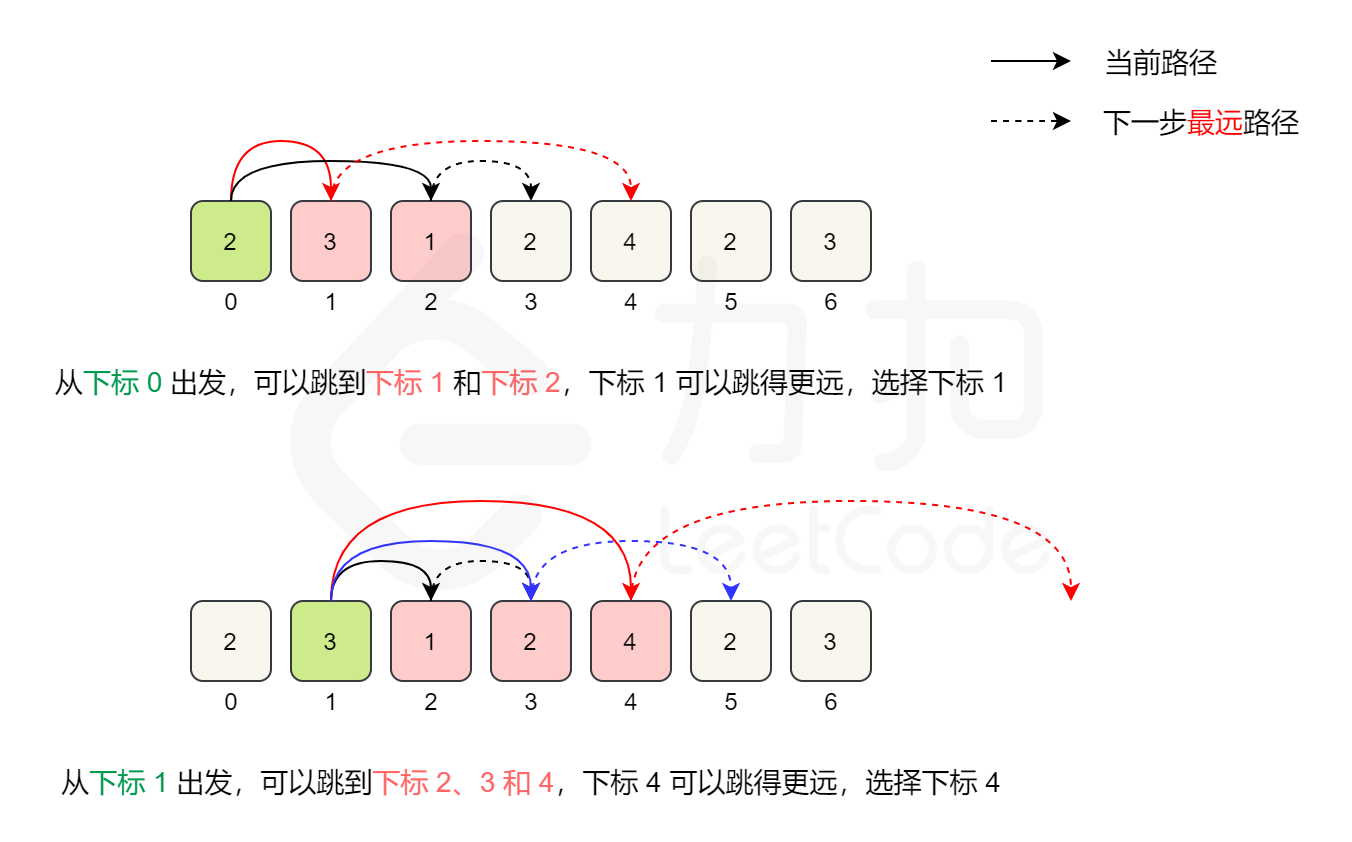
此时我们发现一件事,当我们遍历数组到位置2,即 [1] 的时候,此时跳跃者肯定会从 [3,1] 这个子数组中跳跃到更远的地方;我们记录这个更远的地方为end,当我们遍历到end的时候,跳跃者肯定会从 [ 上一次跳跃的位置, e n d ] [上一次跳跃的位置,end] [上一次跳跃的位置,end] 中一个地方往前跳,哪个点跳的远就从哪个点跳
不难发现,我们每次到达end点,其实之前或者此刻都跳了一次,我们记录这次跳跃。
在程序一开始的时候,只遍历的第一个点,所以只能从第一个点开始跳;
当遍历结束的时候,如果我们遍历第n个点,而此刻end又恰好是第n个点,因为end是上一次跳跃更新的,所以上一次跳跃我们就到达了n点,所以我们不遍历n点,以免多计算一次
复杂度
时间复杂度:
O ( n ) O(n) O(n)
空间复杂度:
O ( 1 ) O(1) O(1)
Code
class Solution:def jump(self, nums: List[int]) -> int:right = 0end = 0n = len(nums)cnt = 0for i in range(n-1):if right < i+nums[i]:right = i+nums[i]if end == i:cnt += 1end = rightreturn cnt
相关文章:

leetcode热题100.跳跃游戏2
Problem: 45. 跳跃游戏 II 文章目录 题目思路复杂度Code 题目 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: …...

【前端】CSS(引入方式+选择器+常用元素属性+盒模型+弹性布局)
文章目录 CSS一、什么是CSS二、语法规范三、引入方式1.内部样式表2.行内样式表3.外部样式 四、选择器1.选择器的种类1.基础选择器:单个选择器构成的1.标签选择器2.类选择器3.id 选择器4.通配符选择器 2.复合选择器1.后代选择器2.子选择器3.并集选择器4.伪类选择器 五…...

迷茫下是自我提升
长夜漫漫,无心睡眠。心中所想,心中所感,忧愁当前,就执笔而下,写下这篇文章。 回忆过往 回想当初为啥学前端,走前端这条路,学校要求嘛,兴趣爱好嘛,还是为了钱。 时间带着…...
用vscode仿制小米官网
html内容: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><link rel&quo…...
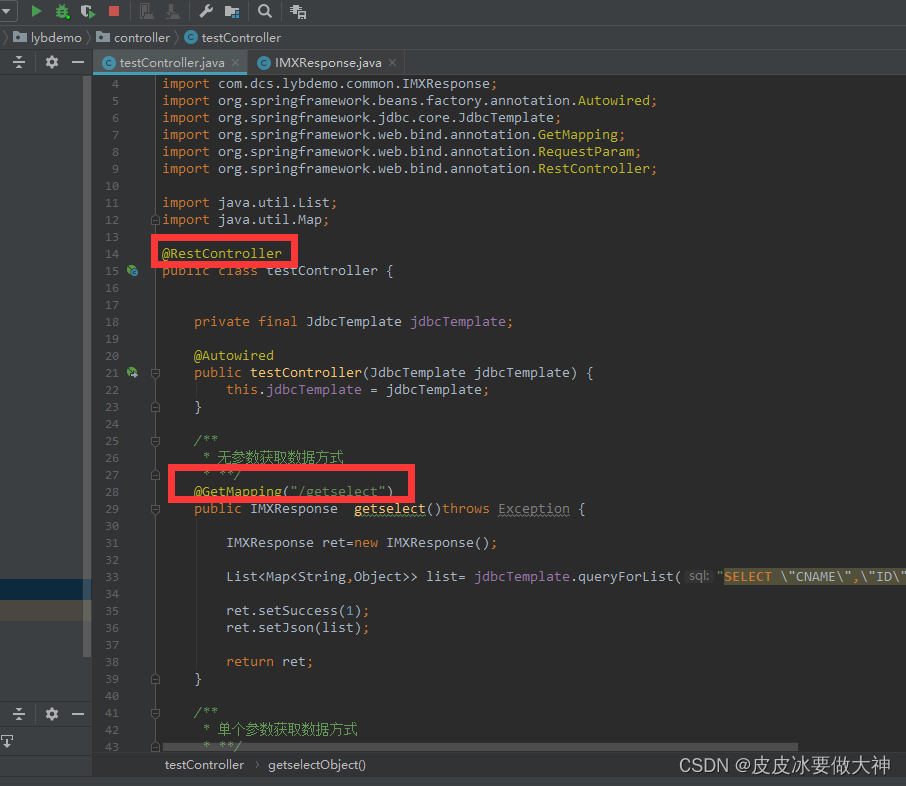
【Java+Springboot】------ 通过JDBC+GetMapping方法进行数据select查询、多种方式传参、最简单的基本示例!
一、JDBC如何使用、PostGresql数据库 1、在pom.xml 先引用jdbc组件。 <!--jdbc--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-jdbc</artifactId></dependency> 2、在pom.xml 再引用p…...

基于单片机光伏太阳能跟踪系统设计
**单片机设计介绍,基于单片机光伏太阳能跟踪系统设计 文章目录 一 概要二、功能设计三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于单片机光伏太阳能跟踪系统的设计,旨在通过单片机技术实现对光伏太阳能设备的自动跟踪,以提高太阳…...
Stable Diffusion 本地化部署
一、前言 最近在家背八股文背诵得快吐了,烦闷的时候,看到使用 AI 进行作图,可以使用本地话部署。刚好自己家里的电脑,之前买来玩暗黑4,配置相对来说来可以,就拿来试试。 此篇是按照 Github 上的 stable-d…...

C++ Algorithm 常用算法
C <algorithm> 头文件是标准库中提供的一系列算法,用于操作范围(range)内的元素。这些算法可以用于数组、容器如vector和list,以及其他满足相应迭代器要求的数据结构。以下是一些常用的C <algorithm> 中的算法及其使用…...

线程安全--深入探究线程等待机制和死锁问题
꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如需转…...

量子计算获重大突破!微软和Quantinuum将量子计算错误率降低800倍,网友:AI算力的希望
量子计算迎来新突破。 近日,微软和量子计算公司Quantinuum宣布:发现了一种新的量子计算系统,可以将传统量子计算的错误率下降800倍,这让高性能量子计算机走进现实更近了一步。 自生成式AI爆发以来,算力是AI发展面临的…...
WordPress 6.5 “里贾纳”已经发布
WordPress 6.5 “里贾纳”已经发布,其灵感来自著名爵士小提琴家Regina Carter的多才多艺。雷吉娜是一位屡获殊荣的艺术家和著名的爵士乐教育家,以超越流派而闻名,她在古典音乐方面的技术基础和对爵士乐的深刻理解为她赢得了大胆超越小提琴所能…...
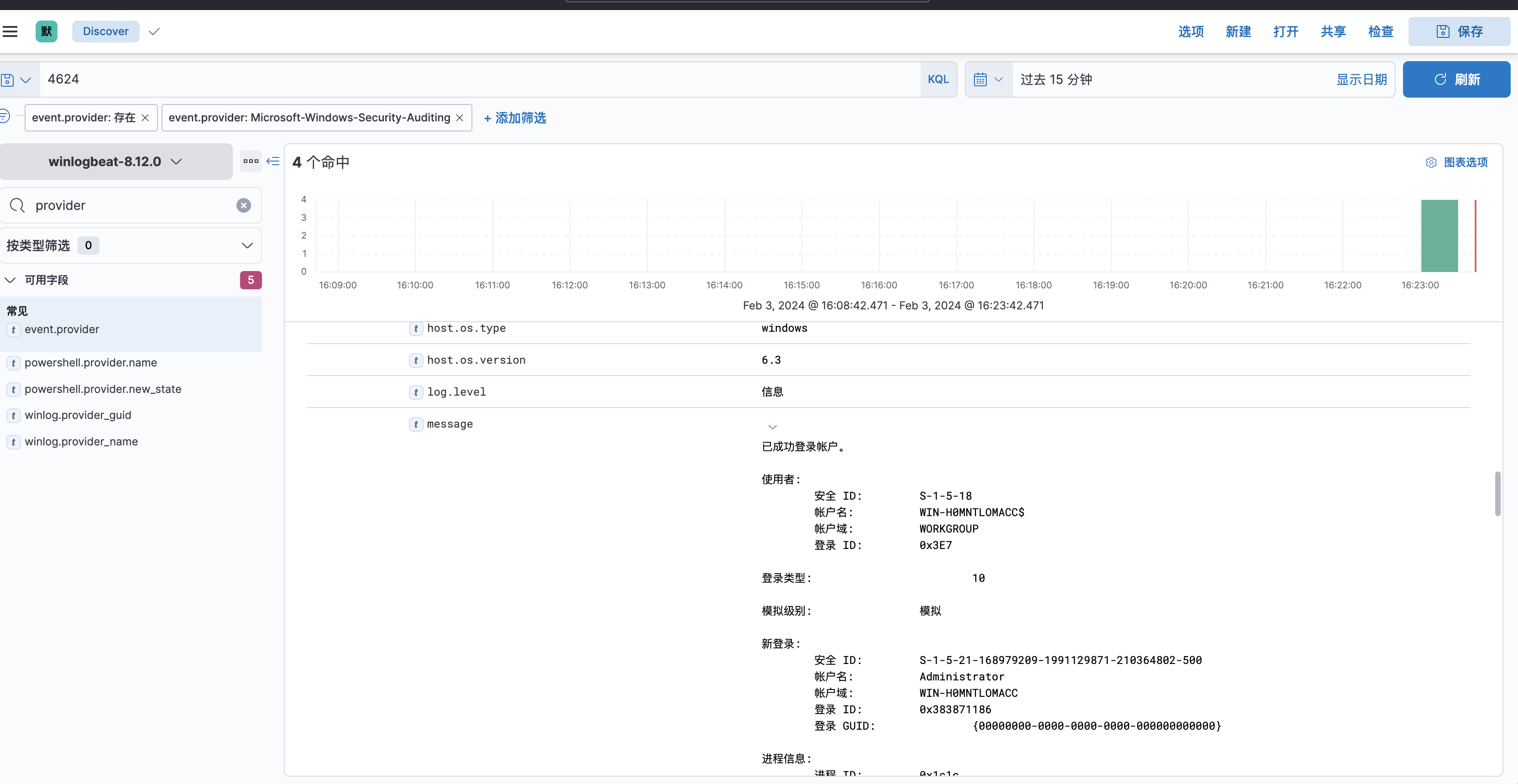
甲方安全建设之日志采集实操干货
前言 没有永远的安全,如何在被攻击的情况下,快速响应和快速溯源分析攻击动作是个重要的话题。想要分析攻击者做了什么、怎么攻击进来的、还攻击了谁,那么日志是必不可少的一项,因此我们需要尽可能采集多的日志来进行分析攻击者的…...
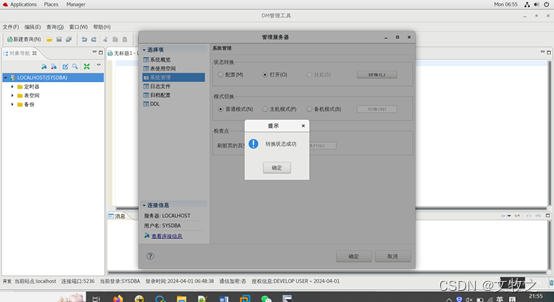
dm8 开启归档模式
dm8 开启归档模式 1 命令行 [dmdbatest1 dm8]$ disql sysdba/Dameng123localhost:5237服务器[localhost:5237]:处于普通打开状态 登录使用时间 : 3.198(ms) disql V8 SQL> select name,status$,arch_mode from v$database;行号 NAME STATUS$ ARCH_MODE ----------…...

“AI复活”背后的数字永生:被期待成为下一个电商,培育市场认知和用户心智还需时间
“AI复活”背后的数字永生:被期待成为下一个电商,培育市场认知和用户心智还需时间© 由 九派新闻 提供 数字永生,还是电子宠物?过去一个月,因包小柏用AI技术让爱女在数字世界“复活”一事,《流浪地球2…...

基于单片机钢琴电子节拍器系统设计
**单片机设计介绍,基于单片机钢琴电子节拍器系统设计 文章目录 一 概要二、功能设计三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于单片机钢琴电子节拍器系统设计是一个综合性的项目,它结合了单片机编程、音频处理、用户界面设计等多个领域的…...

我的创作纪念日(year Ⅱ)
大家好,我是Kamen Black 君,今天我与大家简单分享一下我两年来在CSDN的创作历程。 print("祝大家每天快乐,love and peace!") 机缘 当初写博客是为了记录一些自己大学中做比赛的心得,没想到自己能走到这一步…...
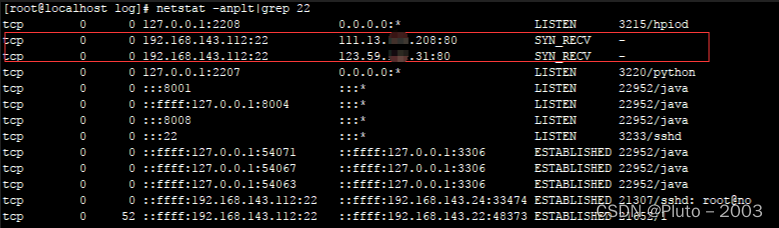
应急响应实战笔记05Linux实战篇(1)
第1篇:SSH暴力破解 0x00 前言 SSH 是目前较可靠,专为远程登录会话和其他网络服务提供安全性的协议,主要用于给远程登录会话数据进行加密,保证数据传输的安全。SSH口令长度太短或者复杂度不够,如仅包含数字&#x…...
重装系统之后,电脑连网卡都没反应怎么办?
前言 有些电脑比较奇葩,安装完成之后会出现网卡连驱动都没有,这时候要安装电脑驱动可是真的烦躁。怎么下手呢? 如果确定电脑的网卡型号还好,直接找个电脑下载个对应的网卡驱动,用U盘复制过去就能安装。 但如果不知道…...
【三十五】【算法分析与设计】综合练习(2),22。 括号生成,77。 组合,494。 目标和,模拟树递归,临时变量自动维护树定义,递归回溯,非树结构模拟树
22. 括号生成 数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 示例 1: 输入:n 3 输出:["((())࿰…...

QT智能指针
一.概述 Qt智能指针是一种能够在不需要手动管理内存的情况下,自动释放资源的指针。它们是C11的std::shared_ptr的一种扩展,可以用于管理Qt对象,尤其是那些不是QObject的对象。 使用智能指针可以避免内存泄露和悬垂指针等问题,同时…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...
