Linux的信号栈的实现(1)
作者
pengdonglin137@163.com
环境
Linux 6.5 + ARM64
概述
在前一篇文章中介绍了Linux系统中的几种栈以及它们之间的切换,进程在用户态和内核态会使用不同的栈,在用户态的主线程和其他线程都有各自的栈,此外进程在执行信号处理程序时也需要栈,那么这个栈来自哪呢?
正文
我们还是以一个多线程的用户态可执行程序为例,先看现象,然后再结合Linux内核源码分析实现。
测试程序
介绍一下这个测试程序multi_thread_signal.c,在主线程里给SIGUSR1注册了处理函数,函数的实现很简单,主要就是打印当前的调用栈。然后主线程又创建了两个从线程,此时存在3个线程,这3个线程分别调用各自的func1、func2和func3,最后在func3中进入sleep,目的是方便我们观察调用栈。
#include <pthread.h>
相关文章:
)
Linux的信号栈的实现(1)
作者 pengdonglin137@163.com 环境 Linux 6.5 + ARM64 概述 在前一篇文章中介绍了Linux系统中的几种栈以及它们之间的切换,进程在用户态和内核态会使用不同的栈,在用户态的主线程和其他线程都有各自的栈,此外进程在执行信号处理程序时也需要栈,那么这个栈来自哪呢? …...
Python学习笔记——heapq
堆排序 思路 堆排序思路是: 将数组以二叉树的形式分析,令根节点索引值为0,索引值为index的节点,子节点索引值分别为index*21、index*22;对二叉树进行维护,使得每个非叶子节点的值,都大于或者…...
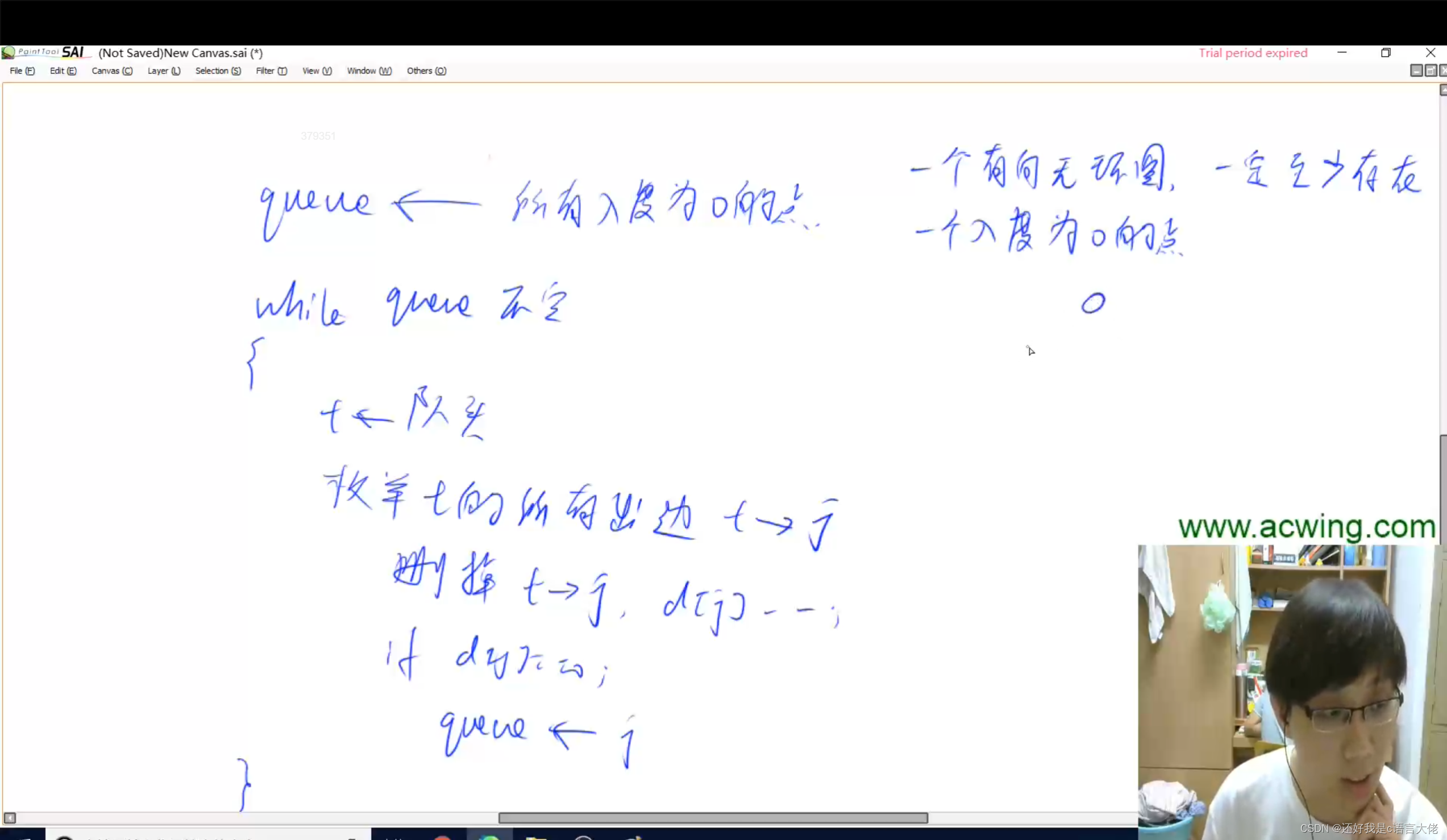
搜索与图论——拓扑排序
有向图的拓扑排序就是图的宽度优先遍历的一个应用 有向无环图一定存在拓扑序列(有向无环图又被称为拓扑图),有向有环图一定不存在拓扑序列。无向图没有拓扑序列。 拓扑序列:将一个图排成拓扑序后,所有的边都是从前指…...

linux CentOS7配置docker的yum源并安装
[TOC](这里写目录标题 配置yum源Docker的自动化安装一些其他启动相关的命令: 配置yum源 使用以下命令下载CentOS官方的yum源文件 wget -O /etc/yum.repos.d/CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-7.repo 清除yum缓存 yum clean all 更新yum缓存…...
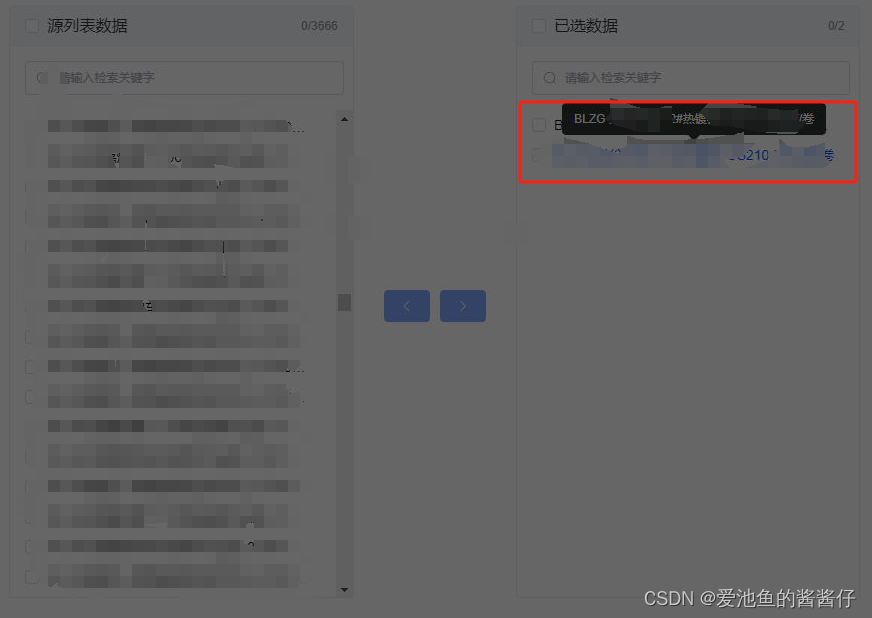
vue结合Elempent-Plus/UI穿梭框更改宽度以及悬浮文本显示
由于分辨率不同会导致文本内容显示不全,如下所示: 因此需要 1、悬浮到对应行上出现悬浮信息 实现代码如下所示: 这里只演示Vue3版本代码,Vue2版本不再演示 区别就在插槽使用上Vue3使用:#default“”;Vu…...

汇川PLC学习Day4:电机参数和气缸控制参数
汇川PLC学习Day4:伺服电机参数和气缸控制参数 一、伺服电机参数二、气缸参数1. 输入IO映射(1)输入IO映射(2) 输入IO触摸屏标签显示映射 2. 输出IO映射(1)输出IO映射(2) …...
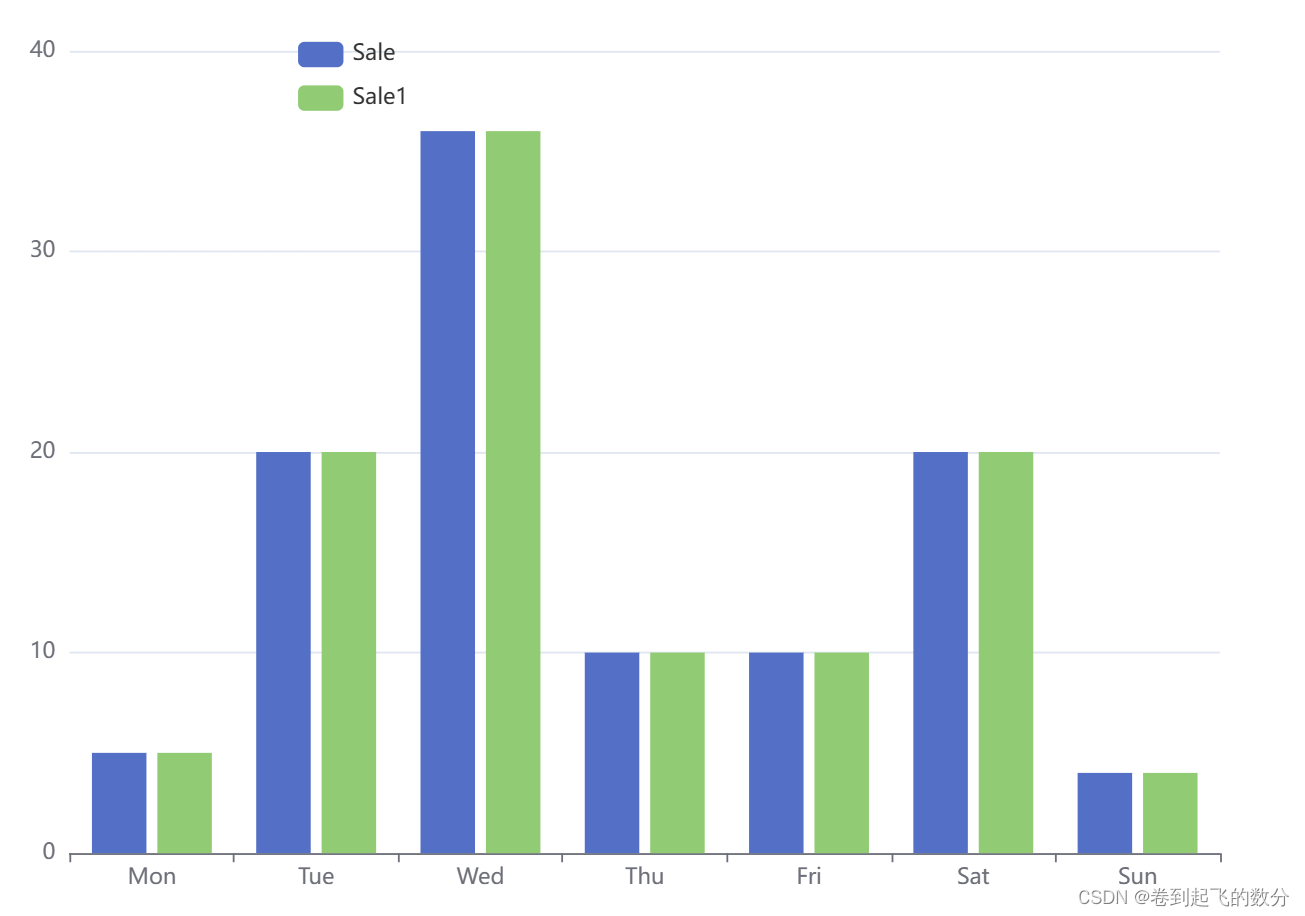
数据可视化高级技术Echarts(快速上手柱状图进阶操作)
目录 1.Echarts的配置 2.程序的编码 3.柱状图的实现(入门实现) 相关属性介绍(进阶): 1.标记最大值/最小值 2.标记平均值 3.柱的宽度 4. 横向柱状图 5.colorBy series系列(需要构造多组数据才能实现…...

【数据结构与算法】力扣 206. 反转链表
题目描述 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 示例 1: 输入: head [1,2,3,4,5] 输出: [5,4,3,2,1]示例 2: 输入: head [1,2] 输出: [2,1]示例 3&#…...

【随笔】Git 高级篇 -- 本地栈式提交 rebase | cherry-pick(十七)
💌 所属专栏:【Git】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! 💖 欢迎大…...

数据结构-- 基于顺序表的通讯录代码讲解
我们了解顺序表之后来一个比较简单的小项目来巩固一下. 每一个函数我都进行了详细的补充, 各位可以仔细阅读。我将整个项目分为了Contact.h 、Contact.c和test.c三个文件中,其中Contact.h用于函数声明和结构体创建,Contact.c用于函数的实现,t…...
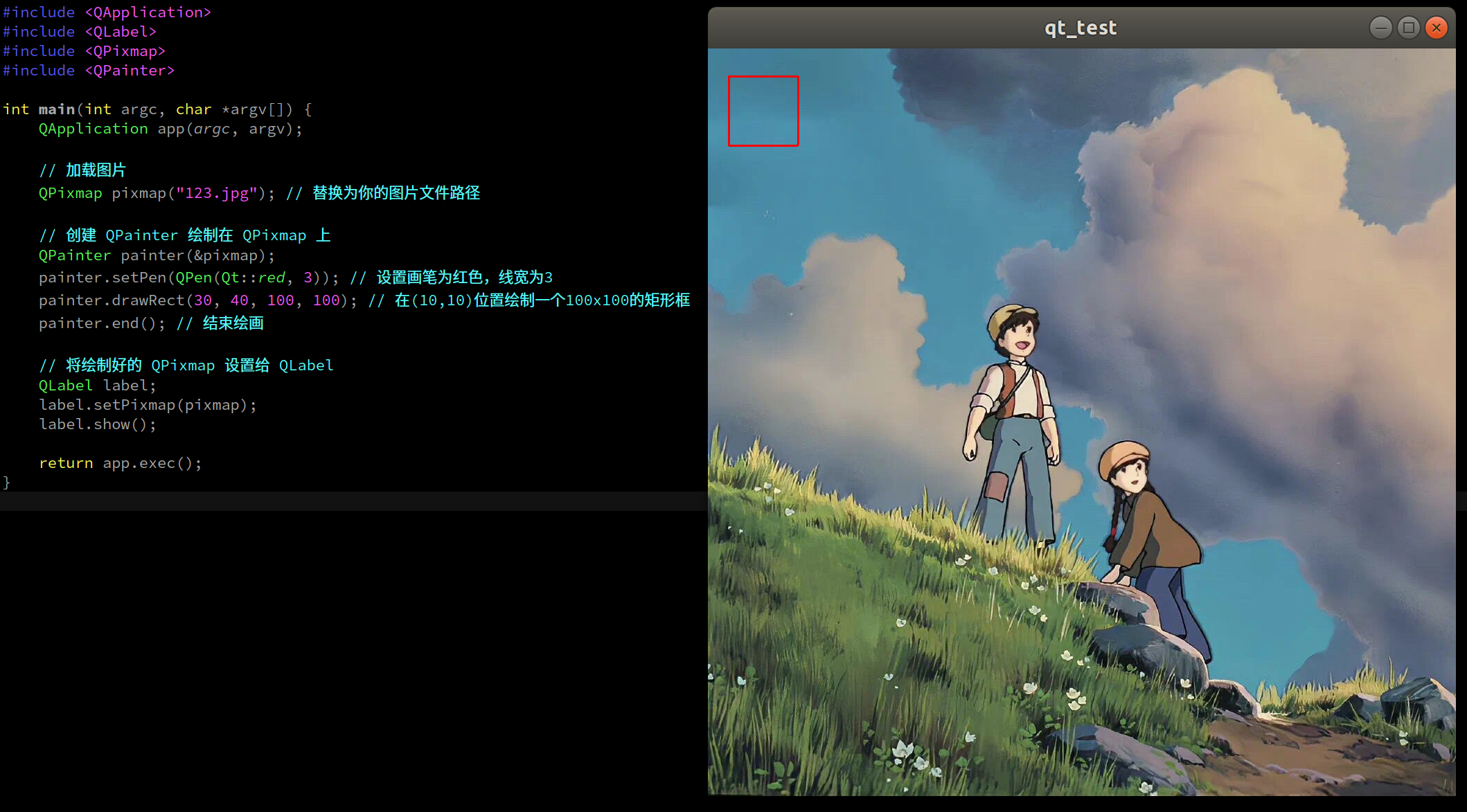
qt-C++笔记之QLabel加载图片
qt-C笔记之QLabel加载图片 —— 2024-04-06 夜 code review! 文章目录 qt-C笔记之QLabel加载图片0.文件结构1.方法一:把图片放在项目路径下,在 .pro 文件中使用 DISTFILES添加图片文件1.1.运行1.2.qt_test.pro1.3.main.cpp 2.方法二:不在 .pr…...
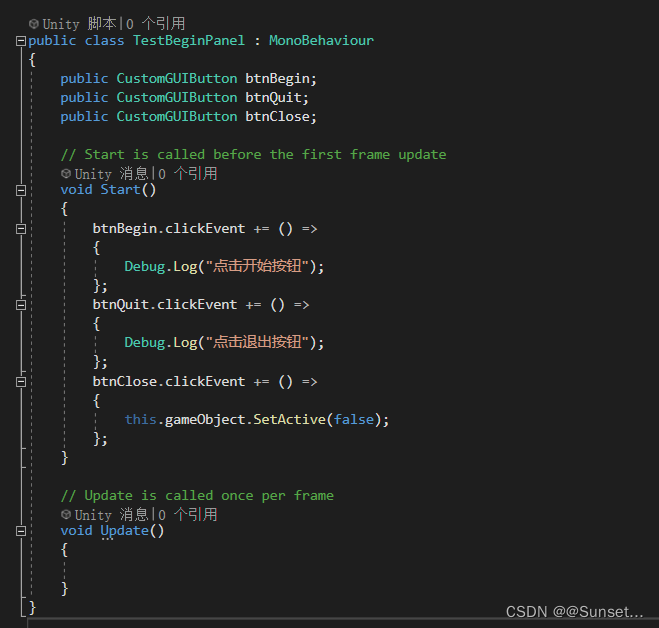
Unity中UI系统1——GUI
介绍 工作原理和主要作用 基本控件 a.文本和按钮控件 练习: b.多选框和单选框 练习: 用的是第三种方法 c.输入框和拖动框 练习: 练习二: e.图片绘制和框 练习: 复合控件 a.工具栏和选择网格 练习: b.滚动视…...

GIt 删除某个特定commit
目的 多次commit,想删掉中间的一个/一些commit 操作方法 一句话说明:利用rebase命令的d表示移除commit的功能,来移除特定的commit # 压缩这3次commit,head~3表示从最近1次commit开始,前3个commit git rebase -i head~3rebase…...

Django --静态文件
静态文件 除了由服务器生成的HTML文件外,WEB应用一般需要提供一些其它的必要文件,比如图片文件、JavaScript脚本和CSS样式表等等,用来为用户呈现出一个完整的网页。在Django中,我们将这些文件统称为“静态文件”,因为…...
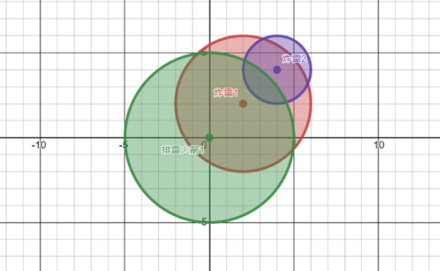
蓝桥杯第十三届省赛C++B组(未完)
目录 刷题统计 修剪灌木 X进制减法 【前缀和双指针】统计子矩阵 【DP】积木画 【图DFS】扫雷 李白打酒加强版 DFS (通过64%,ACwing 3/11); DFS(AC) DP(AC) 砍竹子(X) 刷题统计 题目描述 小明决定从下周一开始努力刷题准…...

编程生活day7--明明的随机数、6翻了、吃火锅
明明的随机数 题目描述 明明想在学校中请一些同学一起做一项问卷调查,为了实验的客观性,他先用计算机生成了N个1到1000之间的随机整数(N≤100),对于其中重复的数字,只保留一个,把其余相同的数…...
css酷炫边框
边框一 .leftClass {background: #000;/* -webkit-animation: twinkling 1s infinite ease-in-out; 1秒钟的开始结束都慢的无限次动画 */ } .leftClass::before {content: "";width: 104%;height: 102%;border-radius: 8px;background-image: linear-gradient(var(…...
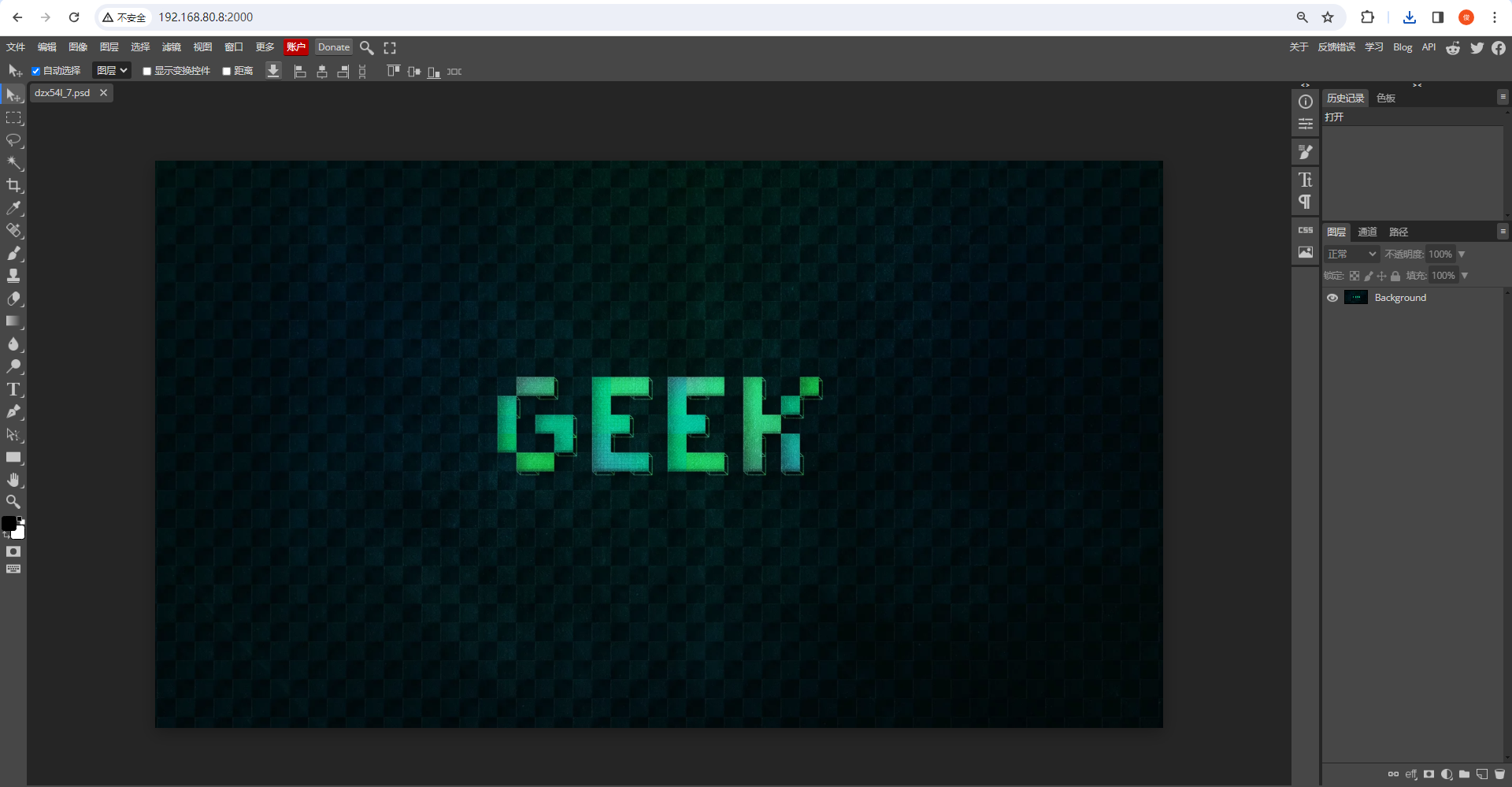
使用 Docker 部署 Photopea 在线 PS 工具
1)Photopea 介绍 GitHub:https://github.com/photopea/photopea 官方手册:https://www.photopea.com/learn/ Adobe 出品的「PhotoShop」想必大家都很熟悉啦,但是「PhotoShop」现在对电脑配置要求越来越高,体积越来越大…...

回溯法(一)——全排列 全组合 子集问题
全排列问题 数字序列 [ l , r ] [l,r] [l,r]区间内元素的全排列问题 extern int ans[],l,r,num;//num:方案数 extern bool flag[]; void dfs(int cl){//cl:current left,即为当前递归轮的首元素if(cl r 1){//数组已越界,本轮递归结束for…...
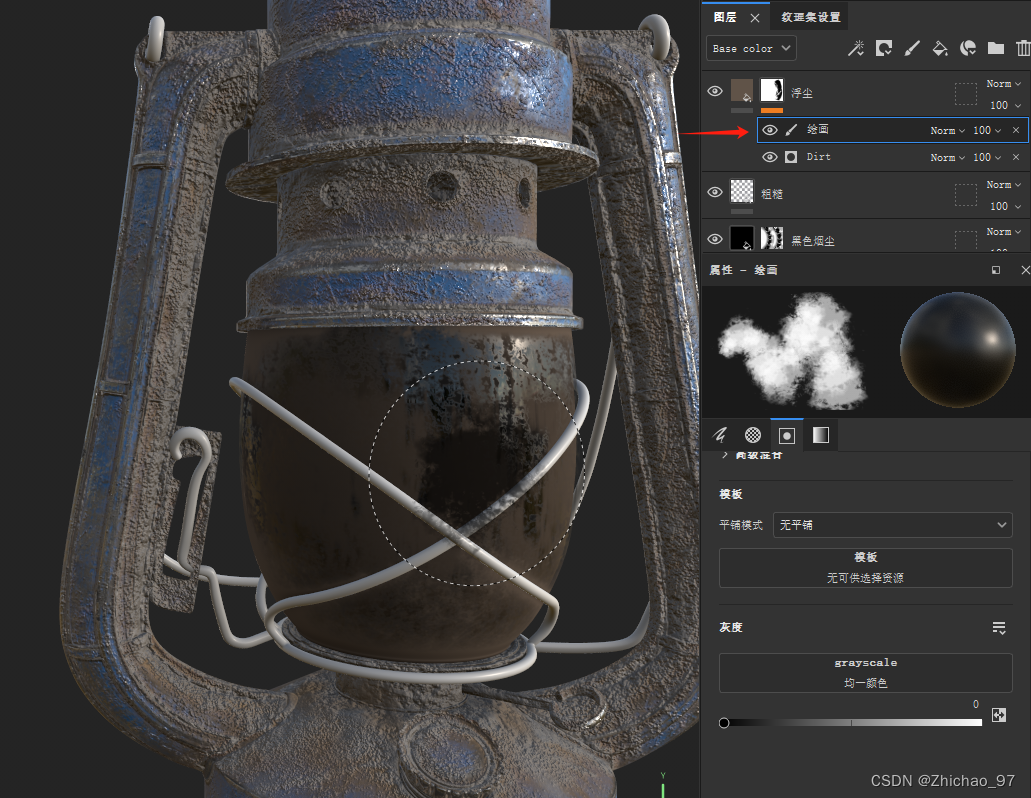
【Pt】马灯贴图绘制过程 04-玻璃脏迹
目录 效果 步骤 一、透明玻璃 二、烟熏痕迹 三、粗糙 四、浮尘 效果 步骤 一、透明玻璃 1. 打开纹理集设置,着色器链接选择“新的着色器链接” 在着色器设置中可以看到此时名称为“Main shader (Copy)” 这里修改名称为“玻璃” 在…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
