【数据结构】数组(稀疏矩阵、特殊矩阵压缩、矩阵存储、稀疏矩阵的快速转置、十字链表)
稀疏矩阵、矩阵压缩、稀疏矩阵的快速转置、十字链表
目录
- 稀疏矩阵、矩阵压缩、稀疏矩阵的快速转置、十字链表
- 1.数组
- 2.数组的顺序表示和实现
- 3.特殊矩阵的压缩存储
- (1). 上三角矩阵—列为主序压缩存储
- (2). 下三角矩阵—**行为主序压缩存储**
- (3). 对称矩阵
- (4). 对角矩阵
- 4. 稀疏矩阵
- 5. 稀疏矩阵的压缩
- (1). 三元组顺序表
- (2). 行逻辑联接的顺序表
- (3). 十字链表
- 6. 稀疏矩阵的转置(普通转置 和 快速转置)
- 方法一(普通转置)复杂度为O(T.mu×T.nu)
- 方法二:快速转置 复杂度O(S.nu+S.tu)
前几期期链接:
- 【数据结构】栈与队列的概念和基本操作代码实现
- 【数据结构】树与二叉树的概念与基本操作代码实现
1.数组
k维数组的定义:
k 维数组 D = { a j 1 , j 2 , . . . , j k } k维数组D=\{ a_{j_1, j_2, ..., j_k} \} k维数组D={aj1,j2,...,jk}
k > 0 称为数组的维数, b i 是数组第 i 维的长度, j i 是数组元素第 i 维的下标 k>0称为数组的维数,b_i是数组第i维的长度,j_i是数组元素第 i维的下标 k>0称为数组的维数,bi是数组第i维的长度,ji是数组元素第i维的下标
a j 1 , j 2 , . . . , j k 属于 E l e m S e t ( 元素的性质相同 ) , Y i = 0 , . . . , b i − 1 ( i = 1 , 2 , … , k ) a_{j_1, j_2, ..., j_k}属于ElemSet(元素的性质相同),Y_{i}=0, ..., b_i -1 ( i=1, 2, …, k) aj1,j2,...,jk属于ElemSet(元素的性质相同),Yi=0,...,bi−1(i=1,2,…,k)
-
数组可以看作是一种特殊的线性表,即线性表数据元素本身又是一个线性表

-
数组特点
数组结构固定,每一维的大小不可变
数据元素同构(元素性质相同) -
数组运算
给定一组下标,存取、修改相应的数据元素,一般不做插入、删除操作。
2.数组的顺序表示和实现
二维数组有两种顺序映象的方式
-
以行序为主序:从数组的第一行开始依次存放每一行的数组元素;存放第i行时,从第一列开始顺次存放
特点:有地址计算公式,可以随机访问
二维数组任意元素的存储地址:
L o c ( a i j ) = L o c ( a 11 ) + [ ( i − 1 ) n + ( j − 1 ) ] ∗ L Loc( a_{ij})=Loc(a_{11})+[(i-1)n+(j-1)]*L Loc(aij)=Loc(a11)+[(i−1)n+(j−1)]∗L
L o c ( a 11 ) 称为基地址或基址 Loc(a_{11})称为基地址或基址 Loc(a11)称为基地址或基址

-
以列序为主序:
二维数组任意元素的存储地址:
L o c ( a i j ) = L o c ( a 11 ) + [ ( j − 1 ) m + ( i − 1 ) ] ∗ L Loc( a_{ij})=Loc(a_{11})+[(j-1)m+(i-1)]*L Loc(aij)=Loc(a11)+[(j−1)m+(i−1)]∗L
L o c ( a 11 ) 称为基地址或基址 Loc(a_{11})称为基地址或基址 Loc(a11)称为基地址或基址
可将二维数组的行为主序和列为主序的存储方式推广到一般情况,可得到 n 维数组数据元素存储位置的映象关系
3.特殊矩阵的压缩存储
宗旨:为值相同的矩阵元素只分配一个空间,对零元不分配存储空间.
(1) 特殊矩阵:非零元在矩阵中的分布有一定规则
- 上(下)三角矩阵
- 对称矩阵
- 对角矩阵
(2.)稀疏阵:零元多,分布无规律
(1). 上三角矩阵—列为主序压缩存储

存储方式:列为主序压缩存储和行为主序压缩存储,存储空间是一维的,将二维数组以一维方式存储。
特点:均可以随机访问数组元素。
上三角矩阵—列为主序压缩存储–数组sa[M]
(1)下三角为0时:
当i≤j时,aij为非0元,存放地址Loc(aij)的计算公式:
L o c ( a i j ) = L o c ( a 11 ) + ( ( j − 1 ) ⋅ j 2 + i − 1 ) ⋅ L , ( c o n d i t i o n : i ≤ j ) Loc(a_{ij})= Loc(a_{11})+(\frac{(j-1)\cdot j}{2}+i-1)\cdot L , (condition:i≤j ) Loc(aij)=Loc(a11)+(2(j−1)⋅j+i−1)⋅L,(condition:i≤j)
一维存储空间用一维数组sa[M]表示, Loc(aij)计算公式(a11存于sa[0],地址为0 ):
L o c ( a i j ) = 0 + ( ( j − 1 ) ⋅ j 2 + i − 1 ) ⋅ 1 , ( c o n d i t i o n : i ≤ j ) Loc(a_{ij})= 0+(\frac{(j-1)\cdot j}{2}+i-1)\cdot 1, (condition:i≤j ) Loc(aij)=0+(2(j−1)⋅j+i−1)⋅1,(condition:i≤j)
数组sa的大小: M = ( n + 1 ) ⋅ n 2 M=\frac{(n+1)\cdot n}{2} M=2(n+1)⋅n

aij(i≤j)存于下标为k的一维数组元素中:
L o c ( a i j ) = k = ( j − 1 ) ⋅ j 2 + i − 1 Loc(aij)=k=\frac{(j-1)\cdot j}{2}+i-1 Loc(aij)=k=2(j−1)⋅j+i−1
(2)下三角为常数时:
常数的存放的位置为: ( n + 1 ) ⋅ n 2 \frac{(n+1)\cdot n}{2} 2(n+1)⋅n
数组sa的大小: M = ( n + 1 ) ⋅ n 2 + 1 M=\frac{(n+1)\cdot n}{2}+1 M=2(n+1)⋅n+1

(2). 下三角矩阵—行为主序压缩存储

存储方式:列为主序压缩存储和行为主序压缩存储,存储空间是一维的,将二维数组以一维方式存储。
行为主序压缩存储:从第一行开始依次存放每一行的“非0(C)元”
特点:均可以随机访问数组元素。
下三角矩阵—行为主序压缩存储–数组sa[M]
(1)上三角为0时:
当 j≤i时,aij为非0元,存放地址Loc(aij)的计算公式:
L o c ( a i j ) = L o c ( a 11 ) + ( ( i − 1 ) ⋅ i 2 + j − 1 ) ⋅ L , ( c o n d i t i o n : j ≤ i ) Loc(a_{ij})= Loc(a_{11})+(\frac{(i-1)\cdot i}{2}+j-1)\cdot L , (condition:j≤i ) Loc(aij)=Loc(a11)+(2(i−1)⋅i+j−1)⋅L,(condition:j≤i)
一维存储空间用一维数组sa[M]表示, Loc(aij)计算公式(a11存于sa[0],地址为0 ):
L o c ( a i j ) = 0 + ( ( i − 1 ) ⋅ i 2 + j − 1 ) ⋅ 1 , ( c o n d i t i o n : j ≤ i ) Loc(a_{ij})= 0+(\frac{(i-1)\cdot i}{2}+j-1)\cdot 1, (condition:j≤i ) Loc(aij)=0+(2(i−1)⋅i+j−1)⋅1,(condition:j≤i)
数组sa的大小: M = ( n + 1 ) ⋅ n 2 M=\frac{(n+1)\cdot n}{2} M=2(n+1)⋅n

aij(i≤j)存于下标为k的一维数组元素中:
L o c ( a i j ) = k = ( i − 1 ) ⋅ i 2 + j − 1 Loc(aij)=k=\frac{(i-1)\cdot i}{2}+j-1 Loc(aij)=k=2(i−1)⋅i+j−1
上三角为常数时:
常数的存放的位置为: ( n + 1 ) ⋅ n 2 \frac{(n+1)\cdot n}{2} 2(n+1)⋅n
数组sa的大小: M = ( n + 1 ) ⋅ n 2 + 1 M=\frac{(n+1)\cdot n}{2}+1 M=2(n+1)⋅n+1

(3). 对称矩阵
存放方式:只存上三角阵或只存下三角阵都可以

地址计算公式 : 参考上三角和下三角矩阵的地址计算公式
(4). 对角矩阵
对角矩阵 –2d+1对角阵:主对角线和主对角线上面d条对角线、主对角线下面d条对角线上的数据元素分布不规律,非0(C).

2d+1 对角阵特点:**第一行和最后一行每行有d+1个数据元素**,余下每行**最多**2d+1个数据元素
压缩存储方法:第一行和最后一行每行存 d+1 个数据元素,余下每行存 2d+1 个数据元素

2d+1-对角阵行为主序压缩存储地址计算公式:
矩阵元素下标从0开始的地址计算公式:
L o c ( a i j ) = L o c ( a 00 ) + ( 2 d + 1 ) ∗ i − d + j − ( i − d ) = L o c ( a 00 ) + ( 2 d + 1 ) ∗ i + j − i Loc(a_{ij})=Loc(a_{00})+(2d+1)*i-d+j-(i-d) =Loc(a_{00})+(2d+1)*i+j-i Loc(aij)=Loc(a00)+(2d+1)∗i−d+j−(i−d)=Loc(a00)+(2d+1)∗i+j−i
0 ≤ i , j < n , ∣ i − j ∣ ≤ d 0≤i,j<n, |i-j|≤d 0≤i,j<n,∣i−j∣≤d
§矩阵元素下标从1开始的地址计算公式:
L o c ( a i j ) = L o c ( a 11 ) + ( 2 d + 1 ) ∗ ( i − 1 ) − d + j − i + d = L o c ( a 11 ) + ( 2 d + 1 ) ∗ ( i − 1 ) + j − i Loc(a_{ij})=Loc(a_{11})+(2d+1)*(i-1)-d+j-i+d= Loc(a_{11})+(2d+1)*(i-1)+j-i Loc(aij)=Loc(a11)+(2d+1)∗(i−1)−d+j−i+d=Loc(a11)+(2d+1)∗(i−1)+j−i
1 ≤ i , j ≤ n , ∣ i − j ∣ ≤ d 1≤i,j≤n, |i-j|≤d 1≤i,j≤n,∣i−j∣≤d
4. 稀疏矩阵
稀疏矩阵: 矩阵元素零元多,在矩阵中随机出现
假设 m行 n列的矩阵含 t个非零元素,则稀疏因子: δ = t m ⋅ n δ =\frac{t}{m\cdot n} δ=m⋅nt
通常认为 δ ≤ 0.05 的矩阵为稀疏矩阵。
压缩存储原则:只存储每个非零元的行、列下标及其值和矩阵的行列维数

常规存储方法缺点:
(1) 零值元素占了很大空间;
(2) 计算中进行了很多和零值的运算,遇除法,还需判别除数是否为零。
解决问题的原则:
(1) 尽可能少存或不存零值元素;
(2) 尽可能减少没有实际意义的运算;
(3) 操作方便。 即:尽可能快地找到与下标值(i,j)对应的元素,尽可能快地找到同一行或同一列的非零值元。
5. 稀疏矩阵的压缩
稀疏矩阵的压缩存储方法:
1. 三元组顺序表
2. 行逻辑联接的顺序表
3. 十字链表
(1). 三元组顺序表
三元表结构:

//三元表结构:
typedef struct{ int i, j; //非零元的行、列下标 int e; //非零元的值
} Triple;//稀疏矩阵的结构
#define MAXSIZE 100 //非零元最大个数
typedef struct{ Triple data[MAXSIZE + 1]; //三元组表,data[0]未用int mu, nu, tu; //矩阵行、列数、非零元个数
} TSMatrix;特点:
有序的双下标法行序有序存储
便于进行依行顺序处理的矩阵运算
若需存取某一行中的非零元,需**从头开始查找**。
压缩存储后,元素aij的存储位置与其下标无关,而取决于之前的非零元个数
非零元以行为主序顺序存放
(2). 行逻辑联接的顺序表
#define MAXRC 500
//行逻辑联接的顺序表
typedef struct {Triple data[MAXSIZE + 1];int rpos[MAXRC + 1]; // 每一行非0元存放的起始位置int mu, nu, tu;
} RLSMatrix; // 行逻辑链接顺序表类型
(3). 十字链表
用三元组表存储稀疏矩阵,在单纯的存储和做类似转置之类的运算时可以节约存储空间,且运算速度较快;
但当进行矩阵相加等运算时,稀疏矩阵的非零元位置和个数都会发生变化。使用三元组表必然会引起数组元素的大量移动。
- 采用链表存放稀疏矩阵的非0元
- 将稀疏矩阵每行的非0元按照列升序的顺序放在一个单链表中
- 将稀疏矩阵每列的非0元按照行升序的顺序放在一个单链表中
即:
稀疏矩阵的每个非0元即位于一个行单链表,也同时位于一个列单链表
用一维数组保存每行非0元的单链表的头指针
用一维数组保存每列非0元的单链表的头指针
十字链表 :每个非零元用含有五个域的结点表示(非零元的所在行、列、值,及同行、同列的下一个非零元)

//十字链表
typedef struct OLNode{ int row, col; //非零元所在行、列int val; //非零元的值struct OLNode*right, *down;//同行、同列的下一个非零元
}OLNode,* OLink;typedef struct{ OLink rhead[M],chead[N]; //行、列指针数组int mu, nu, tu; //行、列数及非零元个数
}CrossList;
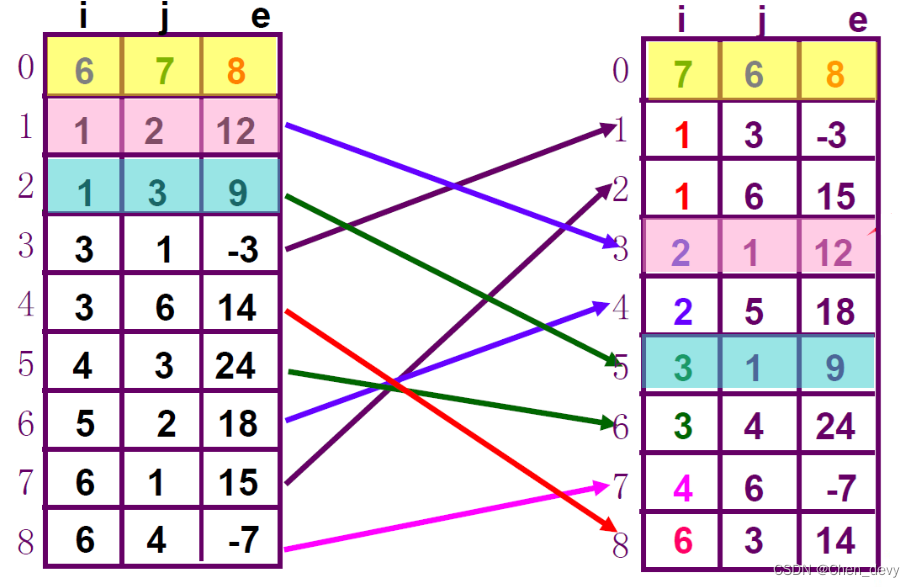
6. 稀疏矩阵的转置(普通转置 和 快速转置)
解决思路:
- 将矩阵行、列维数互换,非零元个数不变
- 将每个三元组中的i和j相互调换,非零元值不变
- 重排次序,使T.data中元素以T的行(M的列)为主序
方法一(普通转置)复杂度为O(T.mu×T.nu)
按矩阵T中三元组表T.data的次序依次在矩阵M的三元组表M.data中找到相应三元组进行转置
为找到M.data中第i列所有非零元素,需对M.data扫描一遍
由于M.data以M行序为主序,所以得到的恰是T.data中应有的顺序
//复杂度为O(T.mu×T.nu)
Status TransposeSMatrix(TSMatrix M, TSMatrix &T){ int col, p, k;T.mu=M.nu; T.nu=M.mu; T.tu=M.tu; if(T.tu){ //有非零元,转置k=1;//k为T.data表下标for(col=1;col<=M.nu;col++)//查找M每一列的非零元for( p=1;p<=M.tu;p++)//扫描M的所有非零元if( M.data[p].j==col ){ T.data[k].i=M.data[p].j;T.data[k].j=M.data[p].i;T.data[k].e=M.data[p].e; k++;}return OK;}return ERROR;
}//T(n)=O(M.nu×M.tu)
//若M.tu与M.mu×M.nu同数量级则 T(n)=O(M.mu×M.nu^2)方法二:快速转置 复杂度O(S.nu+S.tu)
//复杂度O(S.nu+S.tu)
//若S.tu与S.mu×S.nu同数量级则 T(n)=O(S.mu×S.nu)
void TransPose_F(TSMatrix S,TSMatrix &Transpose_S){//S为原来矩阵//Transpose_S为转置后矩阵Transpose_S.mu=S.nu;Transpose_S.nu=S.mu;Transpose_S.tu=S.tu;if(S.tu){//判断是否为空int col;//列int num[MAXSIZE]={0};// 记录原三元组中列号为 col 的项的数目。 辅助数组int cpot[MAXSIZE]={0};// 记录原三元组中列号为 col 的项在新三元组中的首位置。 辅助数组//扫描第一次 记录元素矩阵S中列数为j的个数for(int i=1;i<=S.tu;i++){//记录元素矩阵S中列数为j的个数num[S.data[i].j]++;}cpot[1]=1;//初始化第一个元素的地址//扫描第二次 记录原三元组中列号为 col 的项在新三元组中的首位置for(col=2;col<=S.nu;col++){//列号为 col 的项在新三元组中的首位置cpot[col]=cpot[col-1]+num[col-1];}//扫描第三次 转置for(int t=1;t<=S.tu;t++){col=S.data[t].j;//列数int s=cpot[col];//地址 下标Transpose_S.data[s].e=S.data[t].e;Transpose_S.data[s].i=S.data[t].j;Transpose_S.data[s].j=S.data[t].i;cpot[col]++;//下标 后移}}
}感谢阅读!
前几期期链接:
- 【数据结构】栈与队列的概念和基本操作代码实现
- 【数据结构】树与二叉树的概念与基本操作代码实现
相关文章:
【数据结构】数组(稀疏矩阵、特殊矩阵压缩、矩阵存储、稀疏矩阵的快速转置、十字链表)
稀疏矩阵、矩阵压缩、稀疏矩阵的快速转置、十字链表 目录 稀疏矩阵、矩阵压缩、稀疏矩阵的快速转置、十字链表1.数组2.数组的顺序表示和实现3.特殊矩阵的压缩存储(1). 上三角矩阵—列为主序压缩存储(2). 下三角矩阵—**行为主序压…...
nginx 配置访问地址和解决跨域问题(反向代理)
1、配置访问地址(通过ip访问) //配置ip访问地址 location ^~/auditApp{alias /usr/local/front-apps/cbd/auditApp;index index.html;if (!-e $request_filename) {rewrite ^/(.*) /auditApp/index.html last;break;}} 2、解决跨域问题&…...
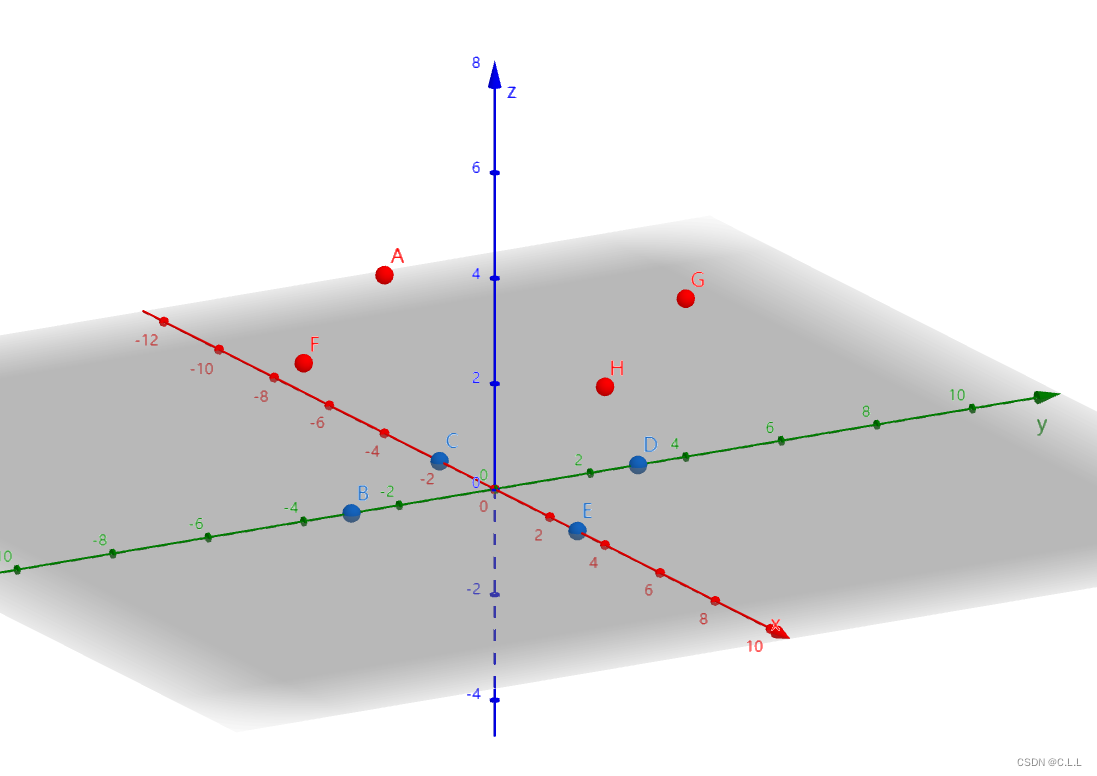
支持向量机(SVM)白话之个人理解(学习记录)
本文仅有文字理解部分,没有相应的数学公式推导过程,便于新手理解。 一、什么是支持向量机 首先我们看下面这张图,在图中圆形和三角形分别代表不同的数据类型,如何画出一条直线使两者能够显著地区分开来呢? 答案可以多…...
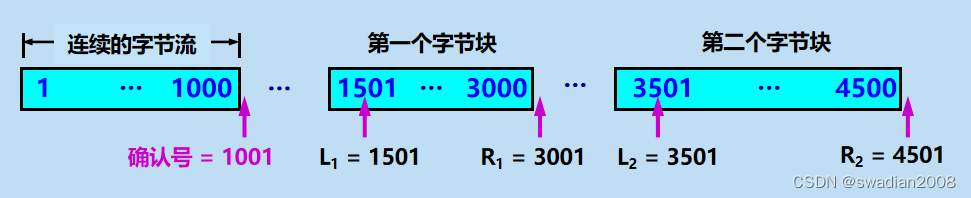
【运输层】TCP 的可靠传输是如何实现的?
目录 1、发送和接收窗口(滑动窗口) (1)滑动窗口的工作流程 (2)滑动窗口和缓存的关系 (3)滑动窗口的注意事项 2、如何选择超时重传时间 (1)加权平均往返…...
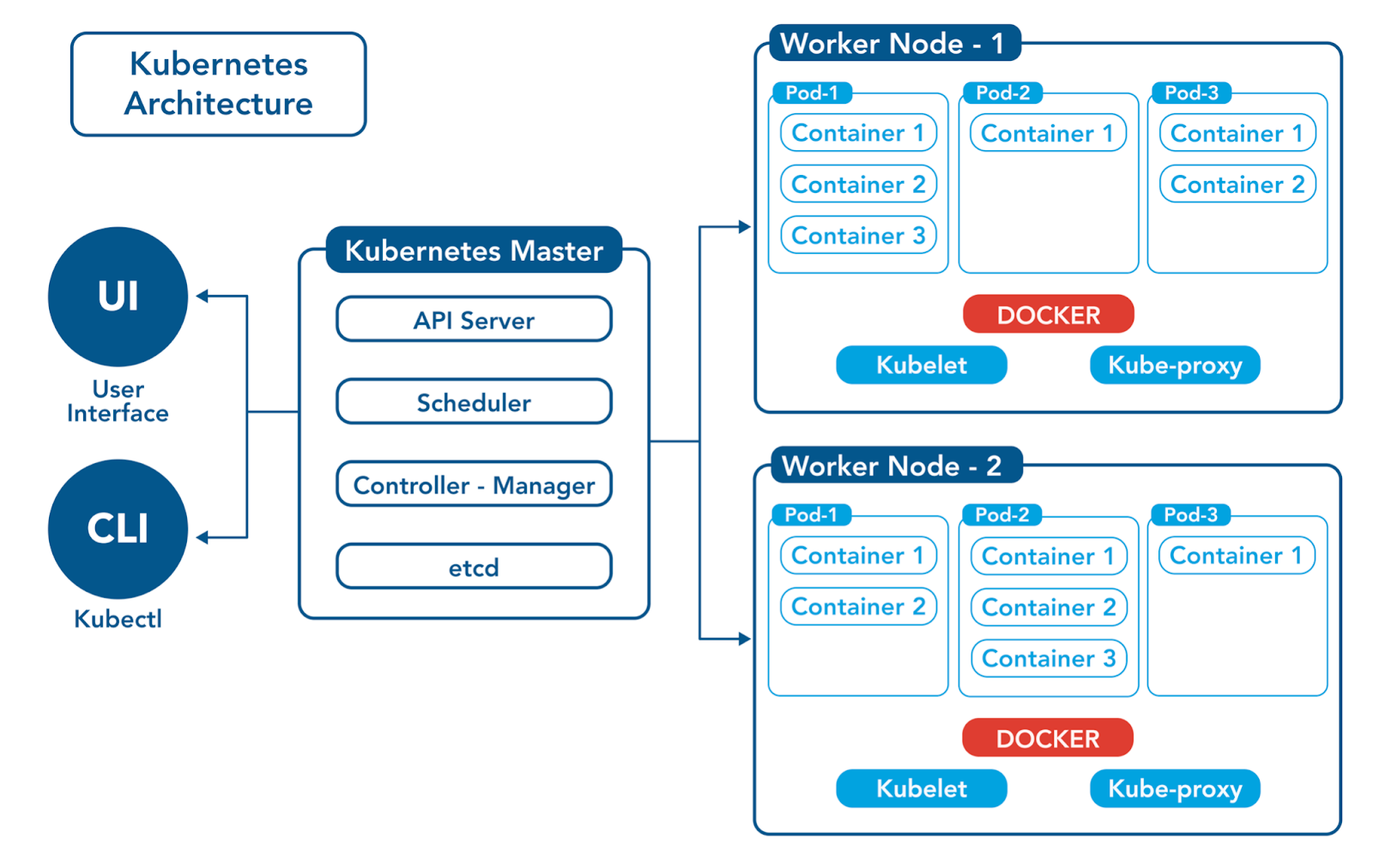
K8s技术全景:架构、应用与优化
一、介绍 Kubernetes的历史和演进 Kubernetes(简称K8s)是一个开源的容器编排系统,用于自动化应用程序的部署、扩展和管理。它最初是由Google内部的Borg系统启发并设计的,于2014年作为开源项目首次亮相。 初始阶段 Kubernetes的诞生…...

Java的异常机制
异常机制 三种类型 检查型异常:程序员无法预见的运行时异常:在编译时会被忽略错误ERROR:错误在代码中被忽略,在编译时检查不到 异常处理机制 抛出异常捕获异常异常处理的五个关键字:try,catchÿ…...
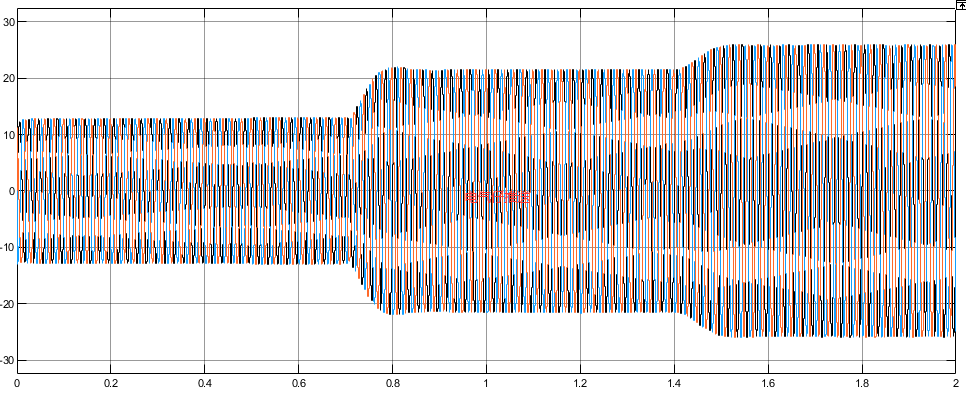
考虑预同步的虚拟同步机T型三电平逆变器并离网MATLAB仿真模型
微❤关注“电气仔推送”获得资料(专享优惠) 模型简介 三相 T 型三电平逆变器电路如图所示,逆变器主回路由三个单相 T 型逆变器组成。 直流侧输入电压为 UPV,直流侧中点电位 O 设为零电位,交流侧输出侧是三相三线制连…...

记一次k8s取证检材过期的恢复
复盘盘古石k8s的时候碰到了证书过期的问题,在此记录解决方法 报错信息:192.168.91.171:6443 was refused - did you specify the right host or port? 查看证书是否过期 kubeadm alpha certs check-expiration或 openssl x509 -in /etc/kubernetes/…...
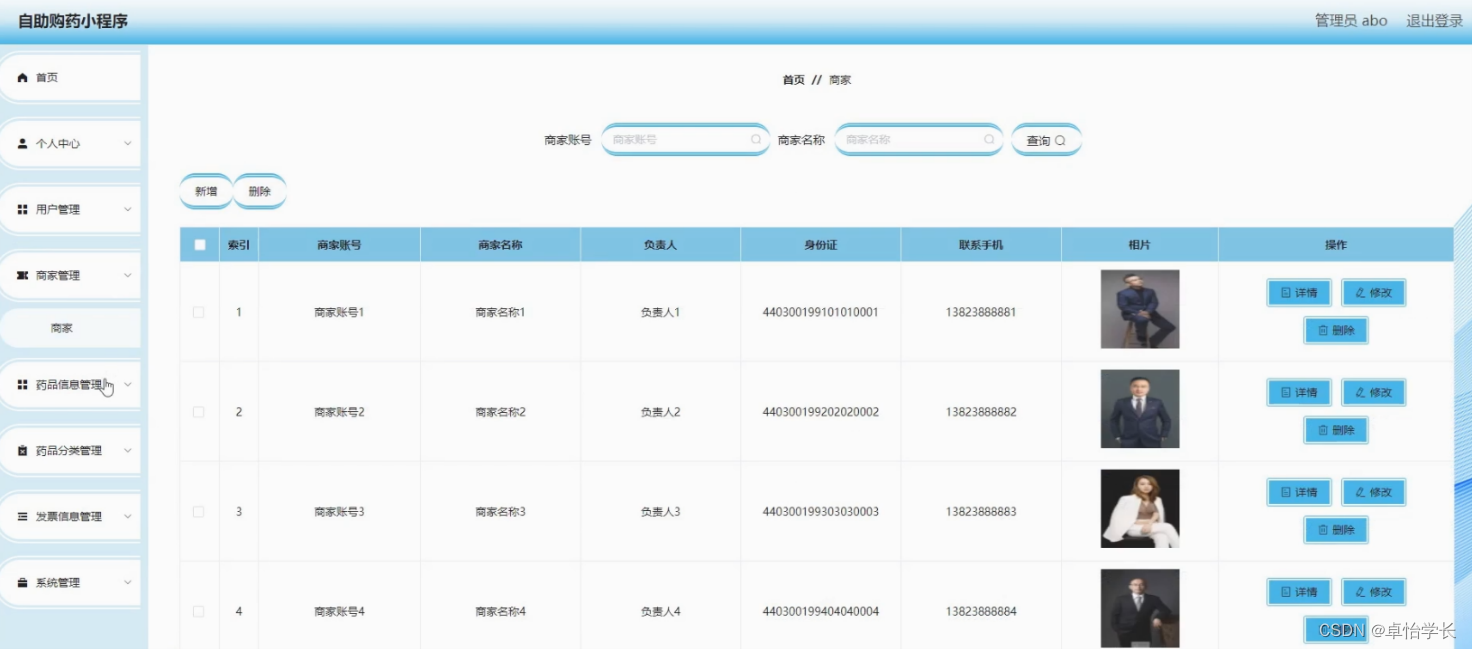
【网站项目】自助购药小程序
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

Ubuntu22.04修改默认窗口系统为X11
Ubuntu22.04安装默认窗口系统为Wayland(通过设置->关于可以看到)。 一、用Ubuntu on Xorg会话登录 用户登录时,点“未列出”,输入用户名后,在登录界面底部的齿轮图标中,选择 "Ubuntu on Xorg&quo…...

延时队列实现实战:如何利用 RabbitMQ 实现延时队列,以满足特定延迟处理需求
实现延时队列,可以通过RabbitMQ的死信队列(Dead-letter queue)特性,“死信队列”是当消息过期,或者队列达到最大长度时,未消费的消息会被加入到死信队列。然后,我们可以对死信队列中的消息进行消…...

关于在Ubuntu上配置mysql踩的一些坑
最近准备换工作了,回顾了下学校时期做的那个webserver,又在linux下mysql踩了一些坑,特此记录下来 程序编译错误mysql.h: No such file or directory 云服务器缺少mysql必要的运行组件,安装: sudo apt-get install l…...
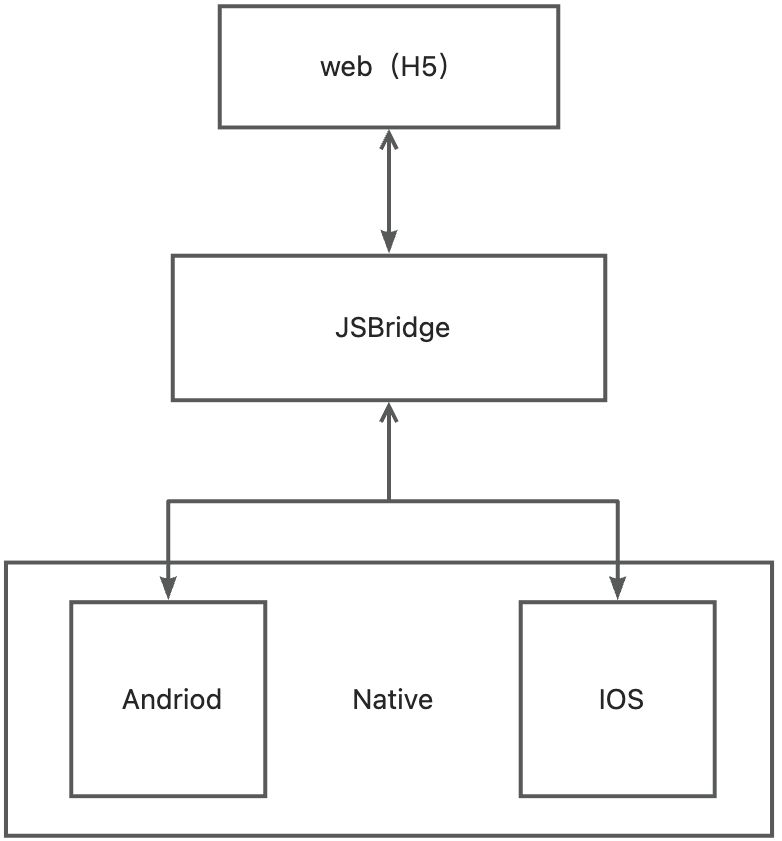
JSBridge原理 - 前端H5与客户端Native交互
1. 概述: 在混合应用开发中,一种常见且成熟的技术方案是将原生应用与 WebView 结合,使得复杂的业务逻辑可以通过网页技术实现。实现这种类型的混合应用时,就需要解决H5与Native之间的双向通信。JSBridge 是一种在混合应用中实现 …...

【Java EE】Spring请求如何传递参数详解
文章目录 🎍传递单个参数🌴传递多个参数🍀传递对象🎄后端参数重命名(后端参数映射)🌲传递数组🎍传递集合🌴传递JSON数据🌸JSON概念🌸JSON的语法&a…...

菜鸟笔记-Numpy常用函数用法汇总
NumPy(Numerical Python的简称)是Python中用于处理数组和矩阵的库,提供了大量的数学函数来操作这些数组。通过前面的学习,慢慢也能发现一些规律,以下是NumPy的一些常用函数及其用法汇总: 数组创建 numpy.a…...
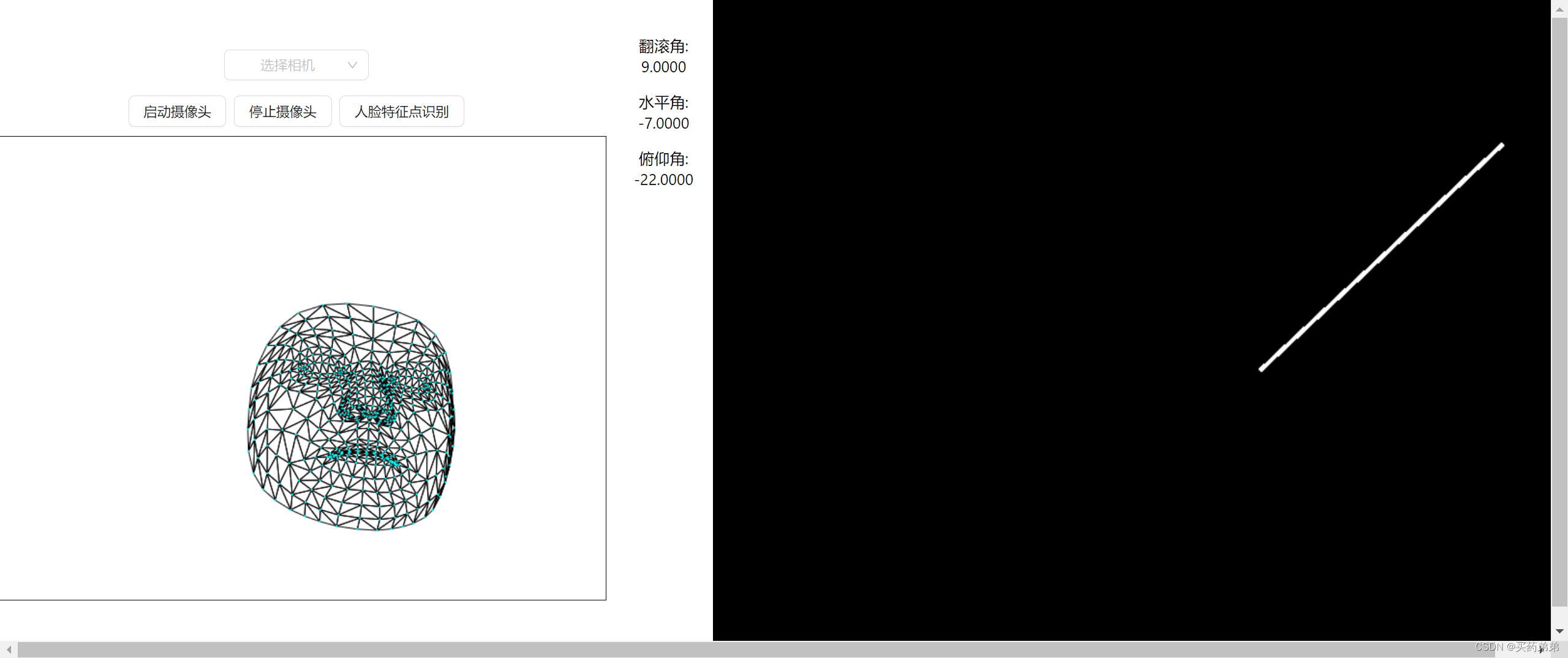
tensorflow.js 如何使用opencv.js通过面部特征点估算脸部姿态并绘制示意图
文章目录 前言一、实现步骤1. 获取所需特征点的索引2. 使用opencv.js 计算俯仰角、水平角和翻滚角cv.solvePnP介绍cv.solvePnP原理运行代码查看效果 3.绘制姿态示意直线添加canvas元素计算姿态直线坐标并绘制 总结 前言 在计算机视觉领域,估算脸部姿态是一项具有挑…...
)
Linux命令-dpkg-divert命令(Debian Linux中创建并管理一个转向列表)
说明 dpkg-divert命令 是Debian Linux中创建并管理一个转向(diversion)列表,其使得安装文件的默认位置失效的工具。 语法 dpkg-divert(选项)(参数)选项 --add:添加一个转移文件; --remove:删除一个转移…...

flex: 1 是哪些属性的缩写?
flex:1是哪些属性的缩写? flex:1 是 flex-grow: 1, flex-shrink: 1,flex-basis: 0% 的缩写; 解释下flex-grow flex-grow是将剩余的空间,根据flex-grow的值平分,然后加到flex-basis上 <!doctype html> <htm…...

python基于opencv实现数籽粒
千粒重是一个重要的农艺性状,通过对其的测量和研究,我们可以更好地理解作物的生长状况,优化农业生产,提高作物产量和品质。但数籽粒数目是一个很繁琐和痛苦的过程,我们现在用一个简单的python程序来数水稻籽粒。代码的…...

OpenCV图像处理——基于OpenCV的ORB算法实现目标追踪
概述 ORB(Oriented FAST and Rotated BRIEF)算法是高效的关键点检测和描述方法。它结合了FAST(Features from Accelerated Segment Test)算法的快速关键点检测能力和BRIEF(Binary Robust Independent Elementary Feat…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...
