最大花之能量(蓝桥杯)
文章目录
- 最大花之能量
- 问题描述
- 动态规划
最大花之能量
问题描述
在一个神奇的王国里,有一个美丽的花园,里面生长着各种奇妙的花朵。这些花朵都有一个特殊的能力,它们能够释放出一种叫做「花之能量」的神秘力量。每朵花的花之能量都不同,它们的能量值用整数表示。
花园里住着四个好朋友:小兰、坤坤、妮妮和依依。他们都非常喜欢花园里的花朵,尤其是那些能量值特别高的花朵。他们认为,只要他们能够找到一种特殊的方法,就可以从花园里的花朵中获得最大的花之能量。
给定花园中的花朵能量序列 (a1,a2 ,…,aN),你需要帮助他们找到一种方法,使得他们能够获得最大的花之能量。这种方法是这样的:从序列中选择一些花朵,组成一个新的序列(ai1 ,ai2 ,…,aiK),其中 1≤i1 <i2<…<iK ≤N,并且这个新序列是一个严格递增序列。
他们的目标是求出这种方法中能够获得的最大花之能量的总和。
你需要编写一个程序,根据给定的花朵能量序列,计算出他们能够获得的最大花之能量的总和。
输入格式
输入的第一行是序列的长度 N。
第二行给出序列中的 N 个整数 a1 ,a2 ,a3 ⋯an ,表示花朵的能量值。
数据范围保证:1≤N≤103,1≤ai ≤104。
输出格式
输出一个整数,表示他们能够获得的最大花之能量的总和。
样例输入
7
8 3 5 9 4 6 7
样例输出
21
动态规划
#include<bits/stdc++.h> // 引入常用的头文件,包含STL库等
using namespace std; // 使用标准命名空间int a[1010],dp[1010]; // 声明两个数组a和dp,大小为1010,a存储花之能量,dp存储状态转移过程中的最大和int main() // 程序的主函数
{int n; // 声明整数变量n,用于保存花朵的总数cin >> n; // 从标准输入读取花朵总数int res = 0; // 声明整数变量res并初始化为0,用于记录最大花之能量的总和// 输入花之能量序列for(int i = 1; i <= n; i++) // 从1遍历到n,读取每朵花的能量cin >> a[i]; // 从标准输入读取每朵花的花之能量并存储在数组a中// 计算最大花之能量的和for(int i = 1; i <= n; i++) // 主循环,从1遍历到n,以计算到第i朵花为止的最大花之能量和{dp[i] = a[i]; // 初始化dp[i]为a[i],表示最小的上升子序列可以只包含自己for(int j = 1; j < i; j++) // 从1遍历到i-1,寻找所有可能的子序列的前一个花朵{if(a[j] < a[i]) // 如果a[j]的能量值小于a[i]的能量值,说明可以形成一个上升子序列dp[i] = max(dp[i], dp[j] + a[i]); // 更新dp[i]为dp[j]+a[i]和dp[i]中较大的值,实现状态转移}res = max(res, dp[i]); // 更新res为res和dp[i]中较大的值,即到目前为止的最大花之能量}cout << res; // 输出最终的最大花之能量return 0; // 主函数返回0,正常结束程序
}
这段代码实现了一个经典的动态规划问题,用于求解最长递增子序列的和。
dp[i]存储了以a[i]为结尾的最长递增子序列的和。- 外部循环用于遍历所有花朵。
- 内部循环用于找到所有小于当前花朵能量值的花朵,并尝试更新
dp[i]。 res变量用于在每次迭代之后保存到目前为止找到的最大和,最后输出该值。
相关文章:
)
最大花之能量(蓝桥杯)
文章目录 最大花之能量问题描述动态规划 最大花之能量 问题描述 在一个神奇的王国里,有一个美丽的花园,里面生长着各种奇妙的花朵。这些花朵都有一个特殊的能力,它们能够释放出一种叫做「花之能量」的神秘力量。每朵花的花之能量都不同&…...
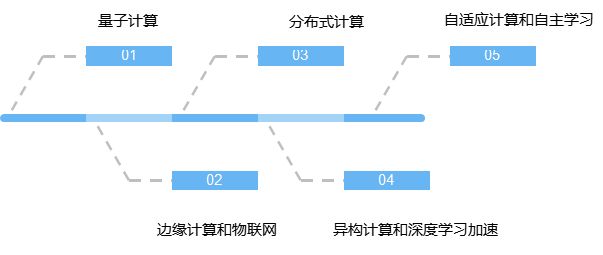
探索算力(云计算、人工智能、边缘计算等):数字时代的引擎
引言 在数字时代,算力是一种至关重要的资源,它是推动科技创新、驱动经济发展的关键引擎之一。简而言之,算力即计算能力,是计算机系统在单位时间内完成的计算任务数量或计算复杂度的度量。随着科技的不断发展和应用范围的不断扩大…...
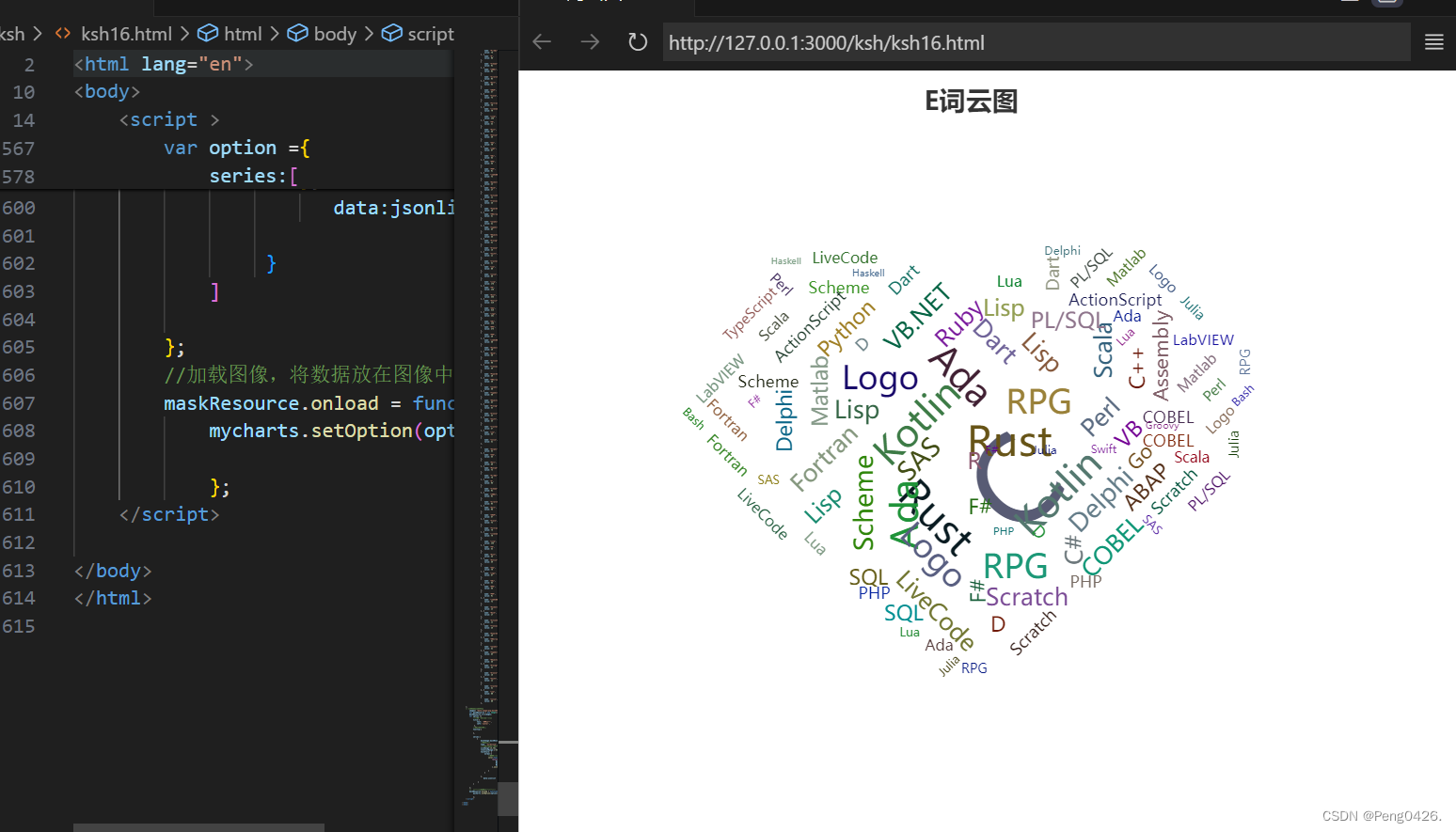
数据可视化-ECharts Html项目实战(10)
在之前的文章中,我们学习了如何在ECharts中编写雷达图,实现特殊效果的插入运用,函数的插入,以及多图表雷达图。想了解的朋友可以查看这篇文章。同时,希望我的文章能帮助到你,如果觉得我的文章写的不错&…...
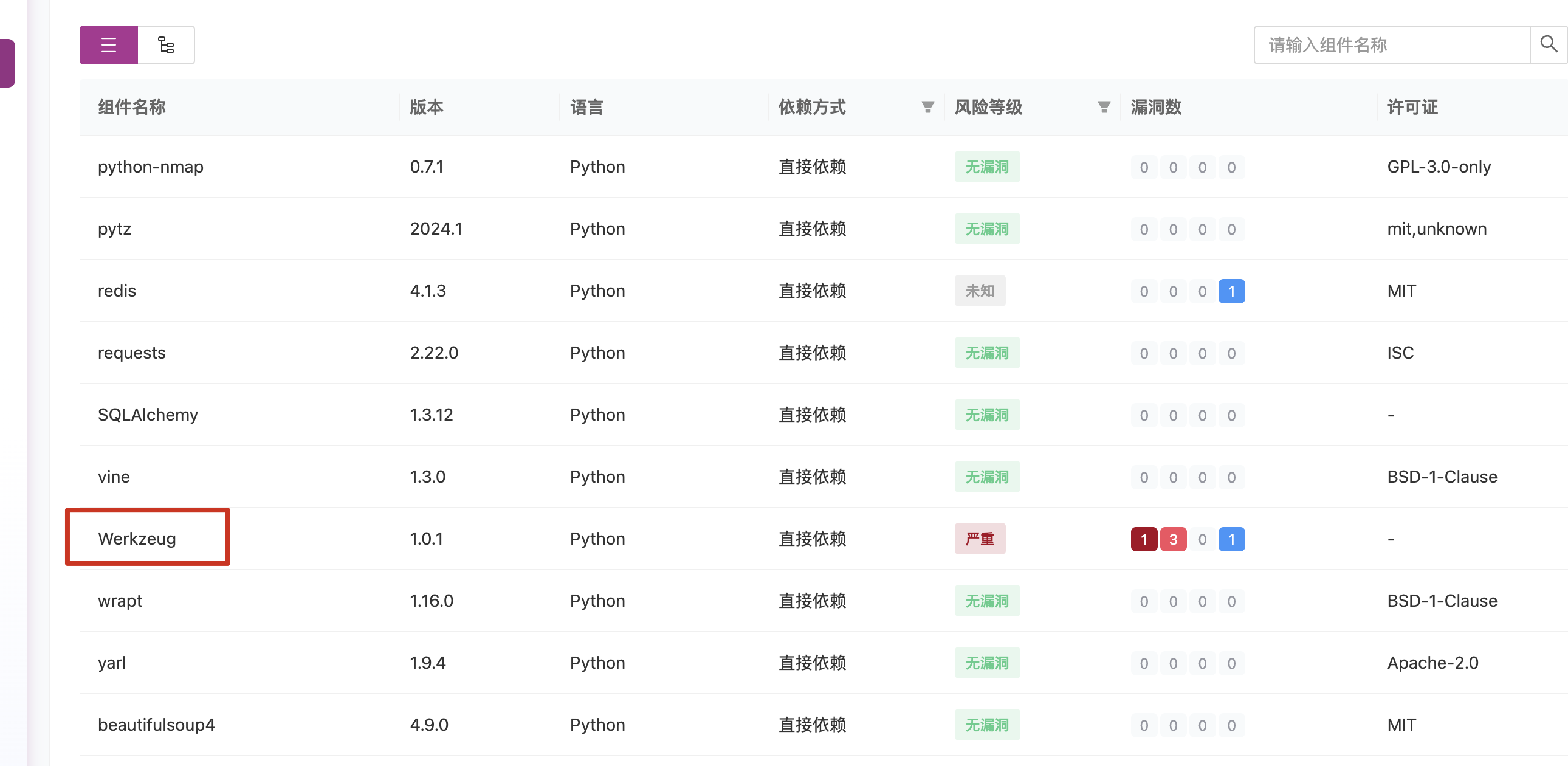
甲方安全建设之研发安全-SCA
前言 大多数企业或多或少的会去采购第三方软件,或者研发同学在开发代码时,可能会去使用一些好用的软件包或者依赖包,但是如果这些包中存在恶意代码,又或者在安装包时不小心打错了字母安装了错误的软件包,则可能出现供…...

[html]网页结构以及常见标签用法
哎,我服了,明明之前学了html的,但时间一长我就忘记了,本来flask学到视图了,但涉及到了html我觉得还是需要重新回顾一下,,,,,, web开发技术栈一共有3门语言。分别是: HTML:译作超文本标记语言&am…...

【C语言】if语句选择题
前言 题目一: 题目二: 题目三: 题目四: 题目五: 题目六: 题目七: 题目八: 前言 关于if语句相关的选择题 题目一: 关于if语句说法正确是:( ) A .if语…...

ZLMediaKit ubantu 下编译
1、获取代码 #国内用户推荐从同步镜像网站gitee下载 git clone --depth 1 https://gitee.com/xia-chu/ZLMediaKit cd ZLMediaKit #千万不要忘记执行这句命令 git submodule update --init二、依赖库 Debian系(包括ubuntu)系统下安装依赖的方法: #除了…...

什么是stable diffusion
机器学习中的稳定扩散 在机器学习中,特别是在深度学习中,稳定扩散可能指的是通过特定的算法,例如深度学习模型,来稳定地生成数据或样本的过程。例如,一些生成模型能够稳定地从高斯分布中采样,以生成高质量的…...

C++ list链表模拟实现
目录 前言: 模拟实现: 迭代器的实现: list类功能函数实现: 初始化成空函数(empty_init): 构造函数: 拷贝构造函数: 尾插(push_back): 插入…...

LangChain - PromptTemplate
文章目录 关于 Prompt关于 PromptTemplate基本创建无变量输入1个变量多变量使用 from_template 自动推断 input_variables 聊天模板使用 from_template 方法构建使用 PromptTemplate 构建 MessagePromptTemplate使用一或多个 MessagePromptTemplates 构建一个 ChatPromptTempla…...
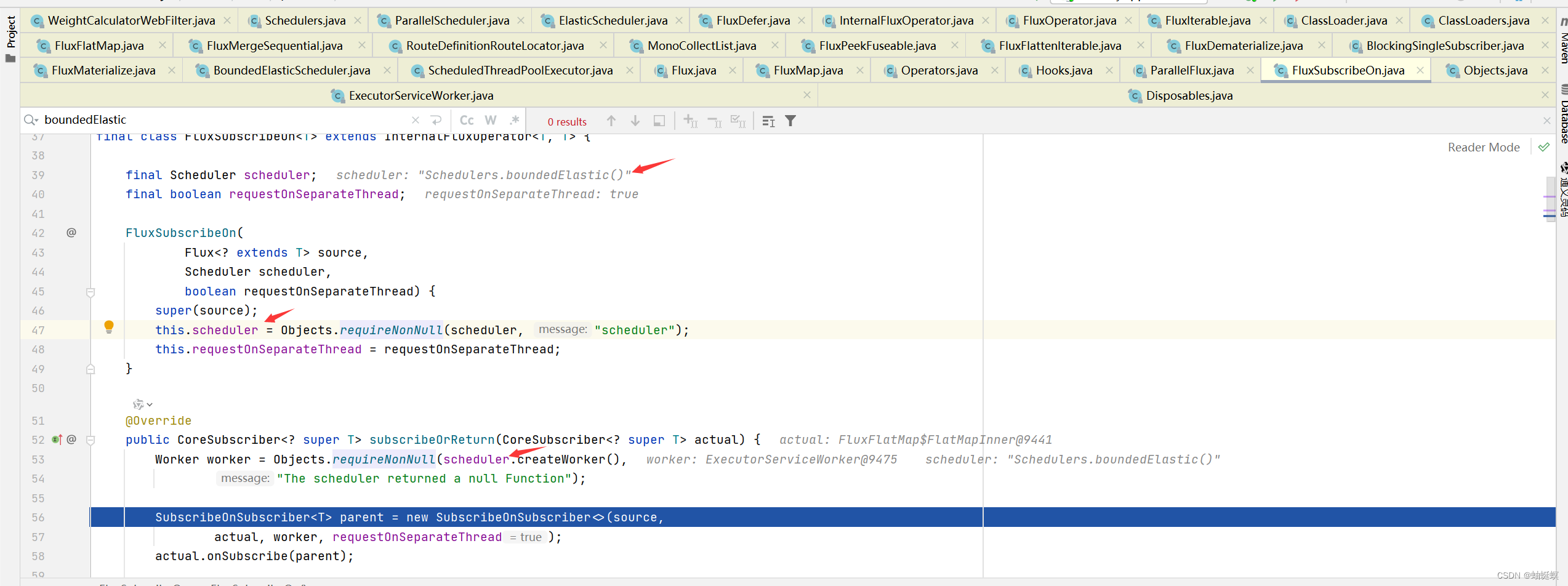
spring cloud gateway openfeign 联合使用产生死锁问题
spring cloud gateway openfeign 联合使用产生死锁问题,应用启动的时候阻塞卡住。 spring.cloud 版本如下 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-dependencies</artifactId><vers…...

【WPF应用37】WPF基本控件-DatePicker的详解与示例
WPF(Windows Presentation Foundation)是微软推出的一个用于构建桌面应用程序的图形子系统。在WPF中,DatePicker控件是一个常用的控件,用于用户选择日期。DatePicker控件提供了一个简洁直观的界面,使用户能够轻松选择日…...
GitHub教程:最新如何从GitHub上下载文件(下载单个文件或者下载整个项目文件)之详细步骤讲解(图文教程)
🐯 GitHub教程:最新如何从GitHub上下载文件(下载单个文件或者下载整个项目文件)之详细步骤讲解(图文教程) 📁 文章目录 🐯 GitHub教程:最新如何从GitHub上下载文件(下载单个文件或者下载整个项目文件)之详细步骤讲解(图…...

编译Nginx配置QUIC/HTTP3.0
1. 安装BoringSSL sudo apt update sudo apt install -y build-essential ca-certificates zlib1g-dev libpcre3 \ libpcre3-dev tar unzip libssl-dev wget curl git cmake ninja-build mercurial \ libunwind-dev pkg-configgit clone --depth1 https://github.com/google/b…...
【JavaWeb】Day38.MySQL概述——数据库设计-DQL
数据库设计——DQL 介绍 DQL英文全称是Data Query Language(数据查询语言),用来查询数据库表中的记录。 查询关键字:SELECT 查询操作是所有SQL语句当中最为常见,也是最为重要的操作。在一个正常的业务系统中,查询操作的使用频次…...

如何使用Java和RabbitMQ实现延迟队列(方式二)?
前言 昨天写了一篇关于Java和RabbitMQ使用插件实现延迟队列功能的文章,今天来讲下另外一种方式,不需要RabbitMQ的插件。 前期准备,需要安装好docker、docker-compose的运行环境。 需要安装RabbitMQ的可以看下面这篇文章。 如何使用PHP和R…...
 将各种数据类型的值转换为它们的字符串)
String.valueOf() 将各种数据类型的值转换为它们的字符串
String.valueOf() 是 Java 中 String 类的一个静态方法,用于将各种数据类型的值转换为它们的字符串表示形式。这个方法在多种情况下都非常有用,特别是当你需要将非字符串类型的值转换为字符串时。 方法签名 String.valueOf() 方法有多个重载版本&#…...

2024-04-08 NO.6 Quest3 自定义交互事件
文章目录 1 交互事件——更改 Cube 颜色2 交互事件——创建 Cube2.1 非代码方式2.2 代码方式 在开始操作前,我们导入上次操作的场景,相关介绍在 《2024-04-08 NO.5 Quest3 手势追踪进行 UI 交互-CSDN博客》 文章中。 1 交互事件——更改 Cube 颜色 …...

素描进阶:深入探索如何表现石膏像的质感
素描进阶:深入探索如何表现石膏像的质感 素描,作为一种古老而经典的绘画方式,历来都被视为是艺术家们探索世界、理解形式与质感的重要工具。而在素描的过程中,如何精准地捕捉并表现物体的质感,是每位艺术家都需要深…...

flutter组件_AlertDialog
官方说明:A Material Design alert dialog. 翻译:一个材料设计警告对话框。 作者释义:显示弹窗,类似于element ui中的Dialog组件。 AlertDialog的定义 const AlertDialog({super.key,this.icon,this.iconPadding,this.iconColor,t…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
