算法学习17:背包问题(动态规划)
算法学习17:背包问题(动态规划)
文章目录
- 算法学习17:背包问题(动态规划)
- 前言
- 一、01背包问题:
- 1.朴素版:(二维)
- 2.优化版:(一维)
- 二、完全背包
- 1.朴素版:(3重for)
- 2.稍微优化版:(二维)
- 3.完全背包问题模版:(最终优化版)
- 三、多重背包
- 1.朴素版:()
- 2.多重背包问题的“二进制优化”:
- 四、分组背包
- 在这里插入图片描述
- 总结
前言

提示:以下是本篇文章正文内容:
一、01背包问题:
1.朴素版:(二维)
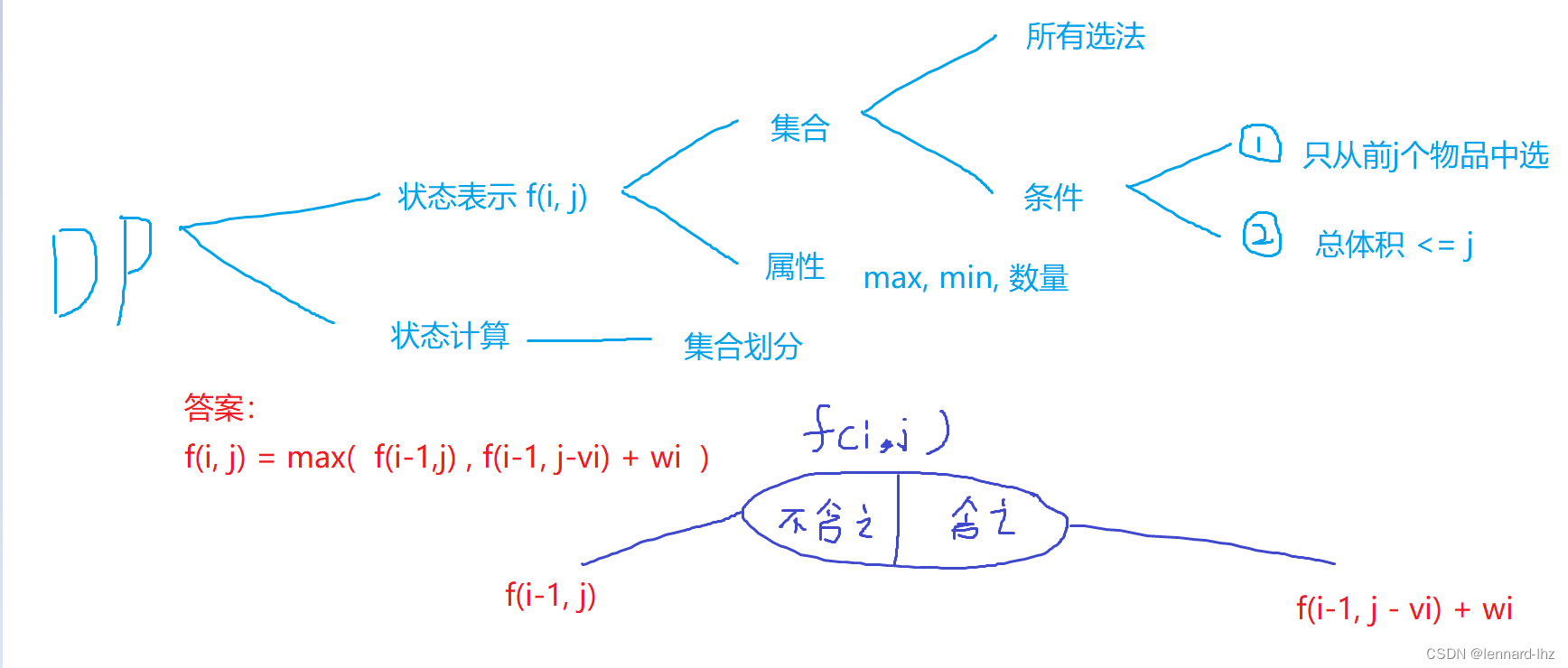

// 例题:有n件物品,和一个容量是m的背包,每件物品只能使用一次。
// 第i件物品的体积是vi,价值是wi,
// 求将哪些物品装入背包,可以使总价值最大。
#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;int n, m;
int v[N], w[N];// v:体积, w:价值
int f[N][N];// 从前i件物品中取,放到容量为j的背包中,最大的价值。 int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i ++)for(int j = 0; j <= m; j ++){f[i][j] = f[i - 1][j];// 不取 if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);// 取 }cout << f[n][m] << endl;return 0;}
2.优化版:(一维)
// 优化版:
#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;int n, m;
int v[N], w[N];// v:体积, w:价值
int f[N];// 从i件物品中去,放到容量为j的背包,最大的价值。
// 注意要执行i轮循环 int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i ++)// 注意1:如果这里不是倒着遍历,那么可能存在,在前面的时候,i物品已经被放进背包了 // 从大到小,保证前面的“状态”,还没有更新过。 for(int j = m; j >= v[i]; j --)// 不取 和 取 f[j] = max(f[j], f[j - v[i]] + w[i]);cout << f[m] << endl;return 0;}
二、完全背包
1.朴素版:(3重for)
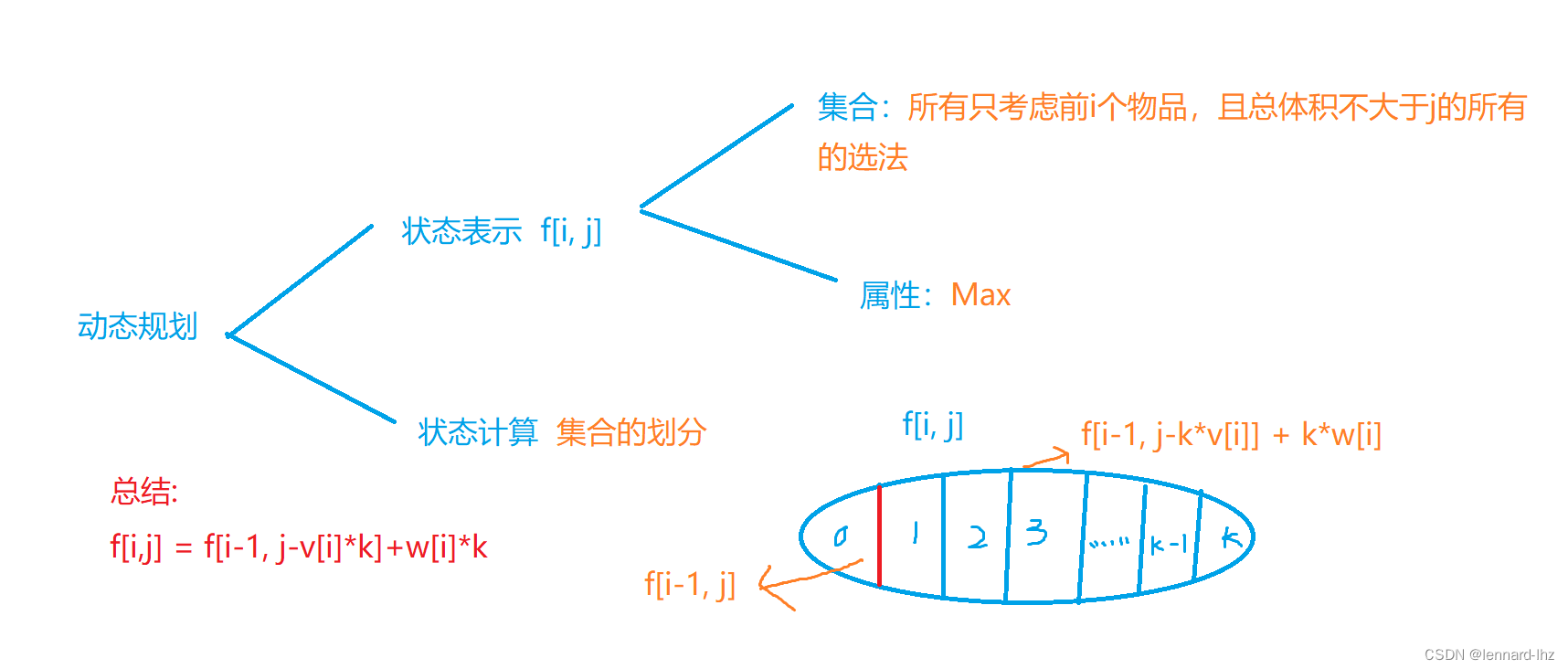
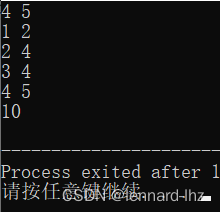
// 例题:有n种物品,容量为m的背包,“每种物品都有无限件可用”。
// 第i件物品的体积是vi,价值是wi,
// 求将哪些物品装入背包,可以使总价值最大,输出最大价值。
#include <iostream>
#include <algorithm>using namespace std; const int N = 1010;int n, m;
int v[N], w[N];
int f[N][N];int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];// 3重for循环: for(int i = 1; i <= n; i ++) for(int j = 0; j <= m; j ++)for(int k = 0; k * v[i] <= j; k ++)f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);cout << f[n][m] << endl;return 0;
}
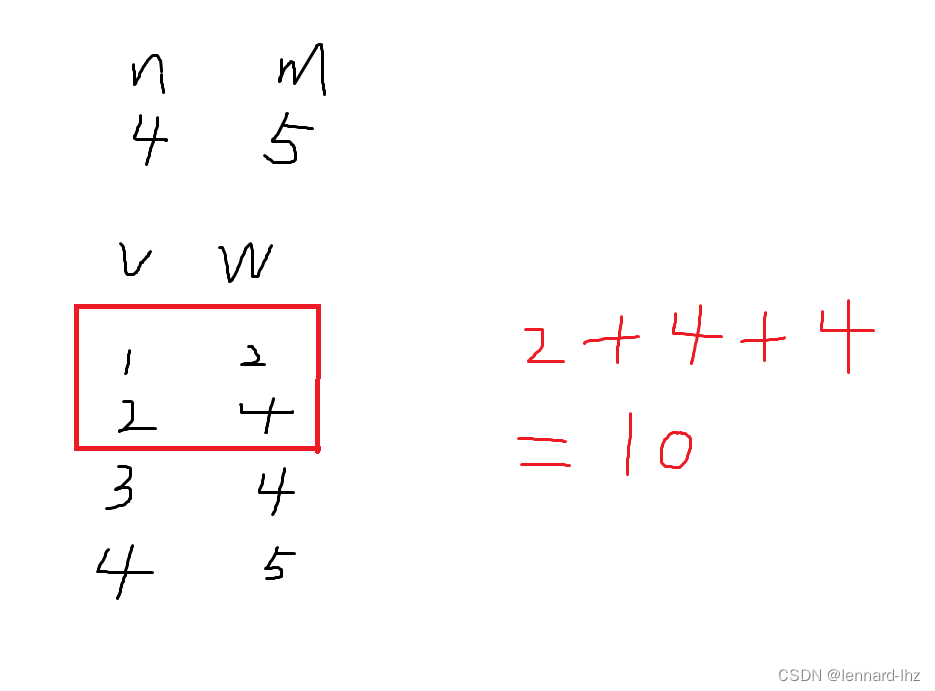
2.稍微优化版:(二维)

#include <iostream>
#include <algorithm>using namespace std; const int N = 1010;int n, m;
int v[N], w[N];
int f[N][N];int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i ++) for(int j = 0; j <= m; j ++){// 这样就和01背包问题有点像了 // 不同的是:f[i - 1][j - v[i]] + w[i] f[i][j] = f[i - 1][j]; // 注意1:要加一个判断条件 (否者越界) if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);}cout << f[n][m] << endl;return 0;
}
3.完全背包问题模版:(最终优化版)
#include <iostream>
#include <algorithm>using namespace std; const int N = 1010;int n, m;
int v[N], w[N];
int f[N];int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];for(int i = 1; i <= n; i ++) // 为什么是从前往后遍历,因为每件物品可以使用无限次,不存在重复问题 for(int j = v[i]; j <= m; j ++)f[j] = max(f[j], f[j - v[i]] + w[i]);cout << f[m]<< endl;return 0;
}
三、多重背包
1.朴素版:()
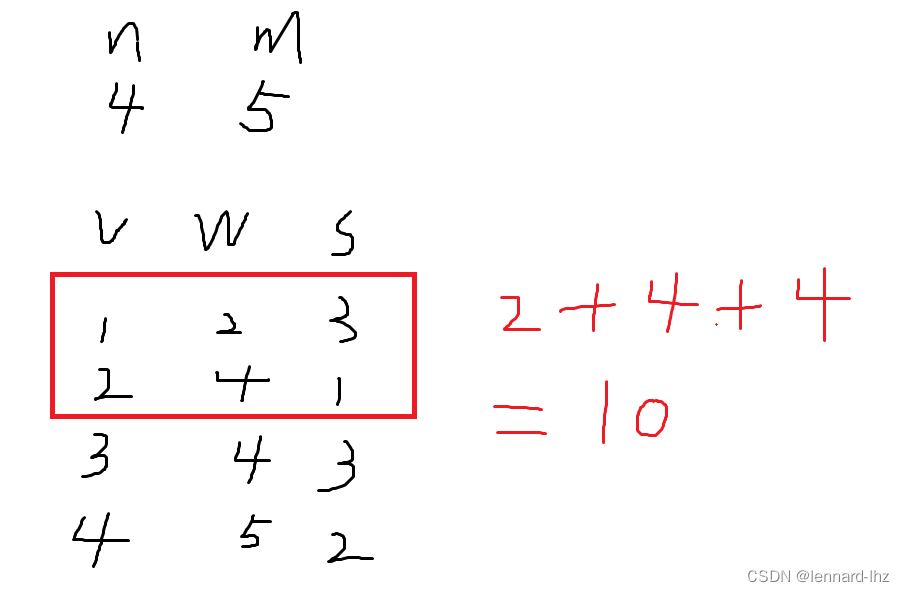
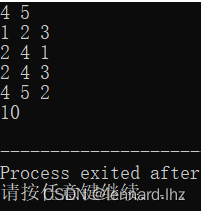
2.多重背包问题的“二进制优化”:

/*
多重背包问题的“二进制优化”:
请先记住:二进制数的组合可以表示一个0~s范围内的十进制数
那么我们将总数量为s的一个“大包裹”转换为“1 2 4 8 16 32 64 .......”这样的小包裹然后对于:这些小包裹,我们选择“取或者不取”,这样就把“多重背包问题”转换为“01背包问题”
*/
/*
注意:为什么要优化?
第一种也可以使用,但是当数据范围大的时候就是出现Time Limit Exceed问题。
(1)0< n, m <100 0< vi, wi, si <100
(2)0 < n <1000 0 < m < 2000 0 < vi, wi, si <2000
const int N = 25000 是如何得到的?1000 * log2(2000) = 1000 * 11 = 22000
*/
#include <iostream>
#include <algorithm>using namespace std;const int N = 25000, M = 2010;int n, m;
int v[N], w[N];
int f[N];int main()
{cin >> n >> m;int cnt = 0;// 标记 :作为打包后的总数量 for(int i = 1; i <= n; i ++){int a, b, s;// 体积,容量,数量 cin >> a >> b >> s;int k = 1;while(k <= s){cnt ++;v[cnt] = a * k;// 打包后的体积 w[cnt] = b * k;// 打包后的容量 s -= k;// 剩余的总数量 k *= 2;// 打包的件数 }if(s > 0)// 多了 {cnt ++;v[cnt] = a * s;w[cnt] = b * s;}}n = cnt;// 打包后的所有包裹的数量// 此时,又相当于01背包问题 for(int i = 1; i <= n; i ++)for(int j = m; j >= v[i]; j --)f[j] = max(f[j], f[j - v[i]] + w[i]); cout << f[m] << endl; return 0;}
四、分组背包
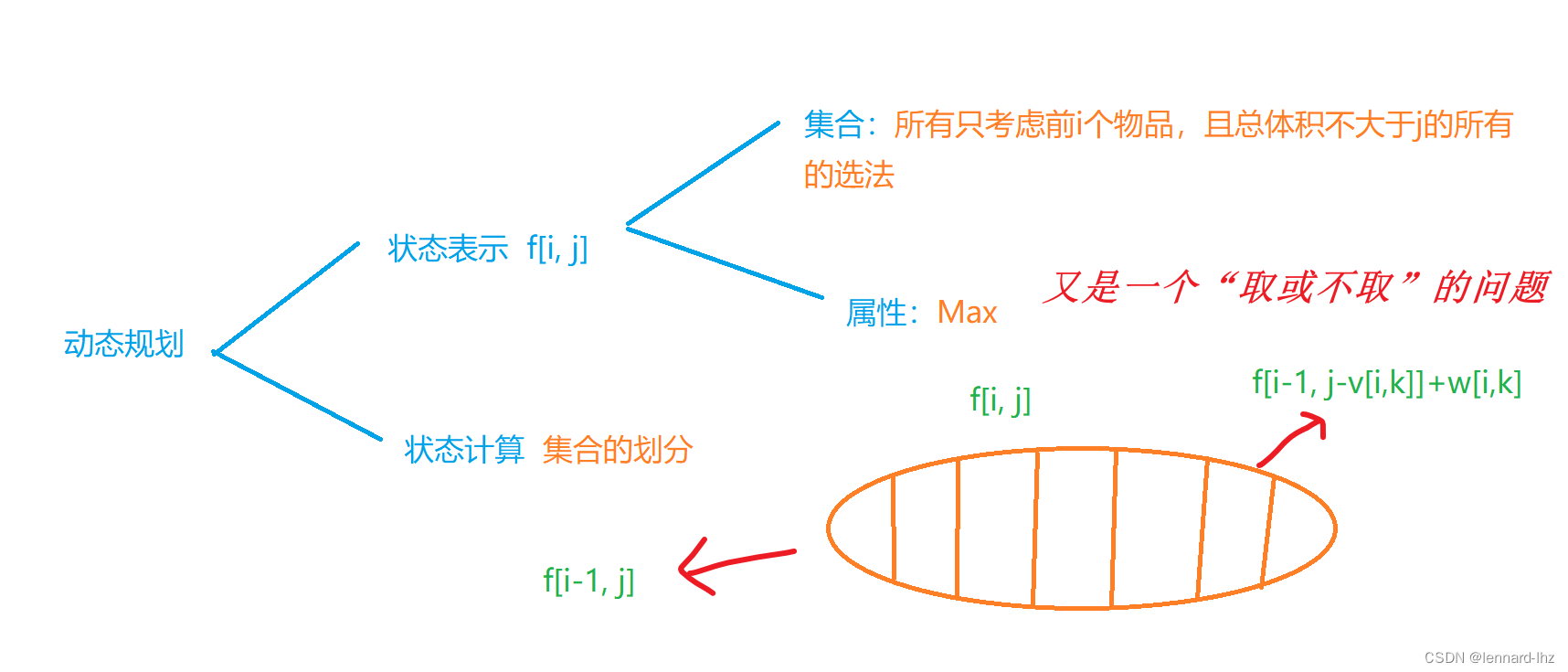

// 有n组物品,容量为m的背包,
// 每组物品有若干个,同一组内的物品最多只能选一个
// 每件物品的体积是vij,价值是wij,其中i是组号,j是组内编号
// 求将哪些物品装入背包,可以使总价值最大,输出最大价值。/*
输入:n,m
接下来n组数据:
第一行:s表示这一组物品的数量
接下来s行:v,w
*/#include <iostream>
#include <algorithm>using namespace std;const int N = 110;int n, m;
int v[N][N], w[N][N], s[N];
int f[N]; int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++){cin >> s[i];for(int j = 0; j <s[i]; j ++)cin >> v[i][j] >> w[i][j];}for(int i = 1; i <= n; i ++)// 像01背包:“取或不取”,只有一件,不可以重复,那么就倒着遍历,保证前面是未更新的 for(int j = m; j >= 0; j --)for(int k = 0; k < s[i]; k ++)if(v[i][k] <= j)f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);cout << f[m] << endl;return 0;}
总结
提示:这里对文章进行总结:
💕💕💕
相关文章:
算法学习17:背包问题(动态规划)
算法学习17:背包问题(动态规划) 文章目录 算法学习17:背包问题(动态规划)前言一、01背包问题:1.朴素版:(二维)2.优化版:(一维…...

axios-mock-adapter使用
文章目录 1. 安装 axios-mock-adapter2. 引入所需的库3. 创建一个模拟适配器实例4. 定义模拟响应5. 在你的代码中使用 axios6. 在测试或开发完成后清理模拟 axios-mock-adapter 是一个用于模拟 axios HTTP 请求的库。它允许你在测试或开发过程中,为 axios 实例提供…...

基于单片机的家用无线火灾报警系统设计
摘 要:针对普通家庭的火灾防范需求,设计一种基于单片机的家用无线智能火灾报警系统。该系统主要由传感器、单片机、无线通信模块、GSM 模块、输入显示模块、声光报警电路和GSM 报警电路组成。系统工作时,检测部分单片机判断是否发生火灾,并将信息通过无线通信模块传…...
--基础知识)
LangChain:索引(Indexes)--基础知识
引言 在当今信息爆炸的时代,如何高效地获取、处理和利用信息成为了关键。LangChain,作为一种先进的语言模型框架,提供了强大的索引功能,帮助用户更好地管理和应用文本数据。本文将详细介绍LangChain索引中的几个核心组件…...
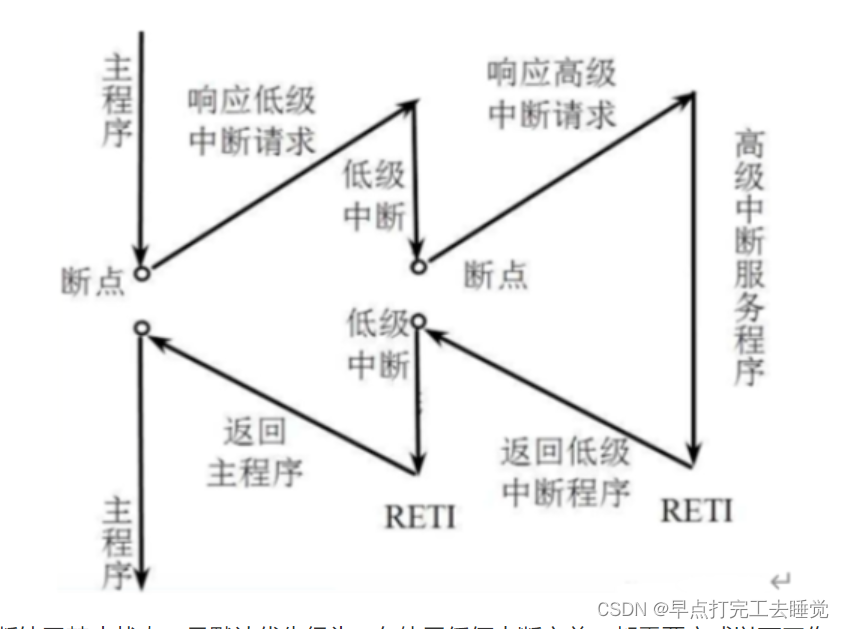
Cortex-M4架构
第一章 嵌入式系统概论 1.1 嵌入式系统概念 用于控制、监视或者辅助操作机器和设备的装置,是一种专用计算机系统。 更宽泛的定义:是在产品内部,具有特定功能的计算机系统。 1.2 嵌入式系统组成 硬件 ①处理器:CPU ②存储器…...
)
对称排序(蓝桥杯)
文章目录 对称排序问题描述模拟 对称排序 问题描述 小蓝是一名软件工程师,他正在研究一种基于交换的排序算法,以提高排序的效率。 给定一个长度为 N 的数组 A,小蓝希望通过交换对称元素的方式对该数组进行排序。 具体来说,小蓝…...

React - 你使用过高阶组件吗
难度级别:初级及以上 提问概率:55% 高阶组件并不能单纯的说它是一个函数,或是一个组件,在React中,函数也可以做为一种组件。而高阶组件就是将一个组件做为入参,被传入一个函数或者组件中,经过一定的加工处理,最终再返回一个组件的组合…...
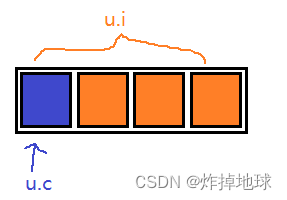
【C语言】结构体、枚举、联合(自定义类型)
文章目录 前言一、结构体1.结构体的声明2.结构体的自引用3.结构体变量的定义和初始化4.结构体成员的访问5.结构体内存对齐(重点)6.#pragma修改默认对齐数7.结构体传参 二、位段1.位段的声明2.位段的内存分配3.位段的跨平台问题 三、枚举四、联合 &#x…...
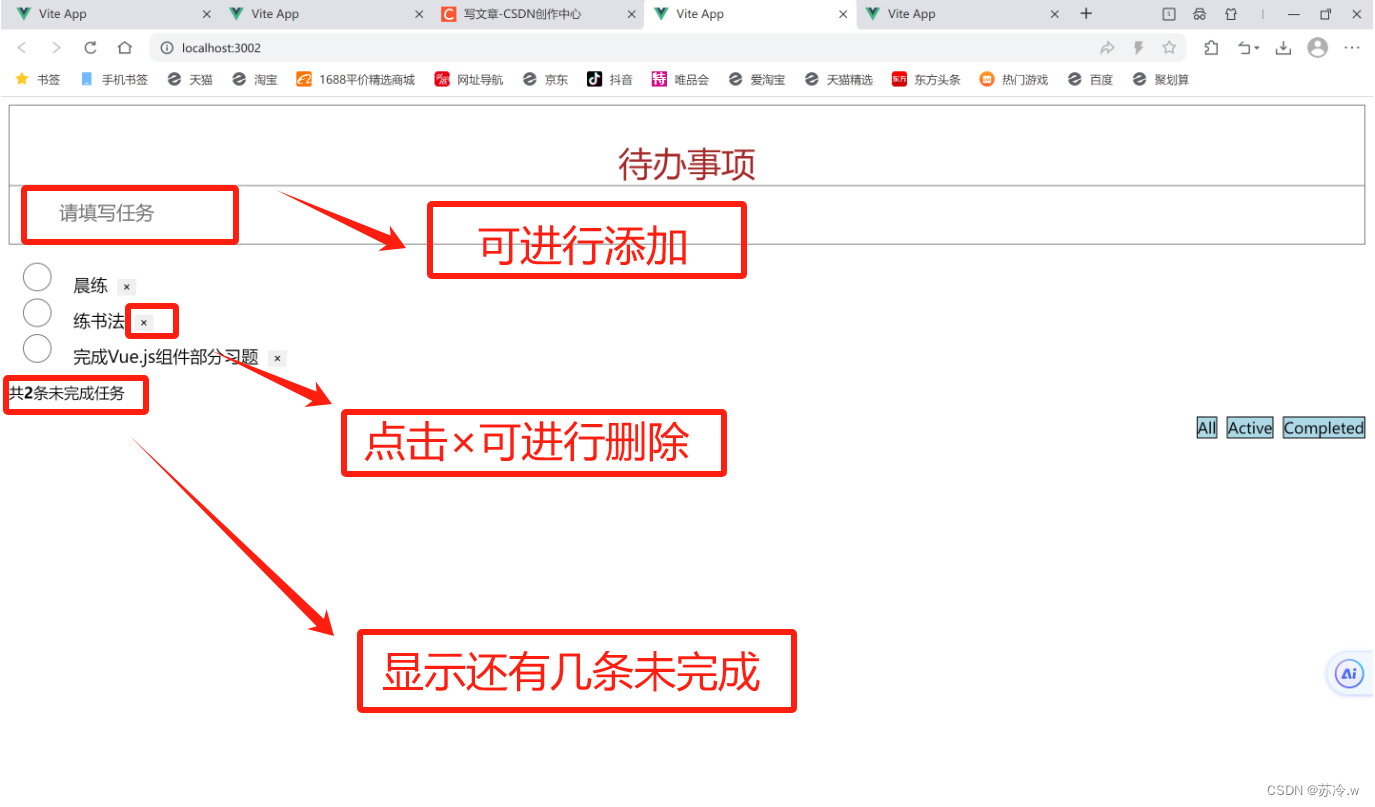
用vue.js写案例——ToDoList待办事项 (步骤和全码解析)
目录 一.准备工作 二.编写各个组件的页面结构 三.实现初始任务列表的渲染 四.新增任务 五.删除任务 六.展示未完成条数 七.切换状态-筛选数据 八.待办事项(全)代码 一.准备工作 在开发“ToDoList”案例之前,需要先完成一些准备工作&a…...
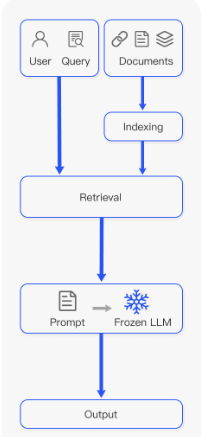
提高大型语言模型 (LLM) 性能的四种数据清理技术
原文地址:four-data-cleaning-techniques-to-improve-large-language-model-llm-performance 2024 年 4 月 2 日 检索增强生成(RAG)过程因其增强对大语言模型(LLM)的理解、为它们提供上下文并帮助防止幻觉的潜力而受…...

Rust 练手小项目:猜数游戏
好久没写 Rust 了,参考《Rust 程序设计语言》写了一下猜数游戏。差不多 40 行,感觉写起来真舒服。 use rand::Rng; use std::{cmp::Ordering, io};fn main() {let secret_number rand::thread_rng().gen_range(0..100);println!("[*] Guess the n…...

蓝桥杯物联网竞赛_STM32L071_16_EEPROM
仍然是没有考过的知识点 朴素的讲就是板子中一块不会因为断电重启而导致数值初始化的一片地址 要注意的是有时候容易把板子什么写错导致板子什么地址写坏了导致程序无法烧录,这个时候记得一直按flash键烧录,烧录时会报错,点击确定࿰…...

复习知识点整理
零碎语法 1.导入某个文件夹的index文件,index可以省略(这里导入的是router和store文件下的index.js文件) 2.路由懒加载 this 1.在vue文件中使用router\store对象时 this:普通函数的this指向vue实例对象(在没有明确指向的时候…...

7款公司电脑监控软件
7款公司电脑监控软件 研究证明,人们在家办公的效率比在办公室办公的效率低一半,其中原因是缺少监督,即便在公司办公,还存在员工偷闲的时刻,比如聊天、浏览无关网站、看剧、炒股等,企业想提高员工的工作效率…...
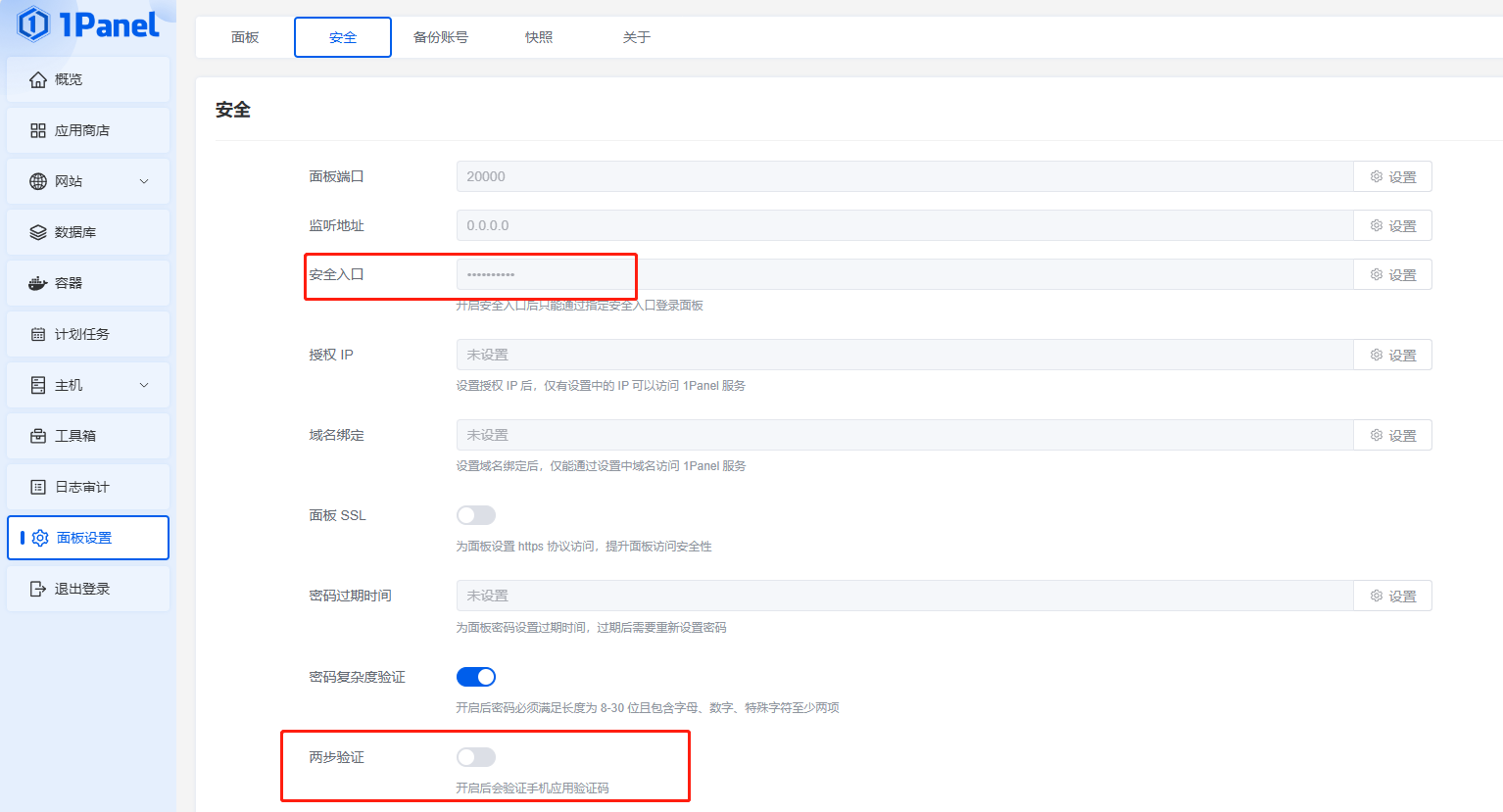
服务器 安装1Panel服务器运维管理面板
服务器 安装1Panel服务器运维管理面板 SSH链接服务器安装1Panel 出现此提示时输入目标路径,须以“/”开头,默认:/opt,本例:/www。 出现此提示时输入目标端口,须未被使用的端口,默认࿱…...
)
最大花之能量(蓝桥杯)
文章目录 最大花之能量问题描述动态规划 最大花之能量 问题描述 在一个神奇的王国里,有一个美丽的花园,里面生长着各种奇妙的花朵。这些花朵都有一个特殊的能力,它们能够释放出一种叫做「花之能量」的神秘力量。每朵花的花之能量都不同&…...
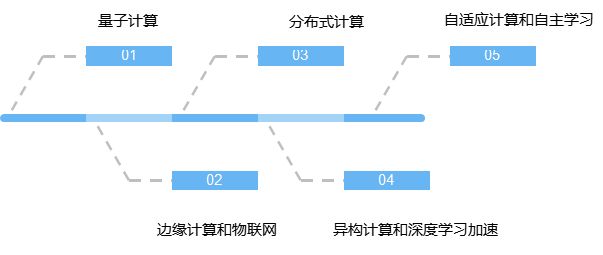
探索算力(云计算、人工智能、边缘计算等):数字时代的引擎
引言 在数字时代,算力是一种至关重要的资源,它是推动科技创新、驱动经济发展的关键引擎之一。简而言之,算力即计算能力,是计算机系统在单位时间内完成的计算任务数量或计算复杂度的度量。随着科技的不断发展和应用范围的不断扩大…...
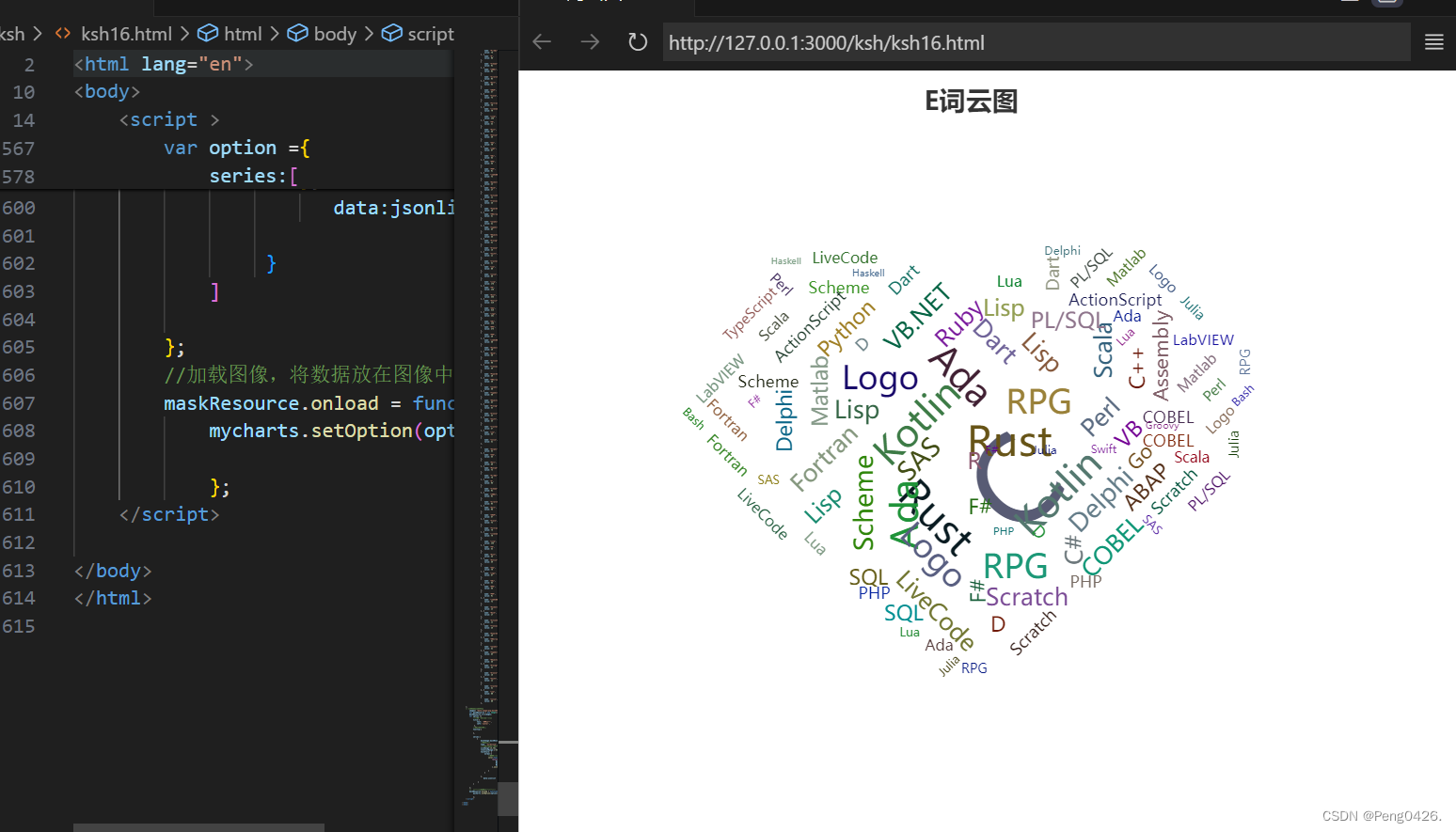
数据可视化-ECharts Html项目实战(10)
在之前的文章中,我们学习了如何在ECharts中编写雷达图,实现特殊效果的插入运用,函数的插入,以及多图表雷达图。想了解的朋友可以查看这篇文章。同时,希望我的文章能帮助到你,如果觉得我的文章写的不错&…...
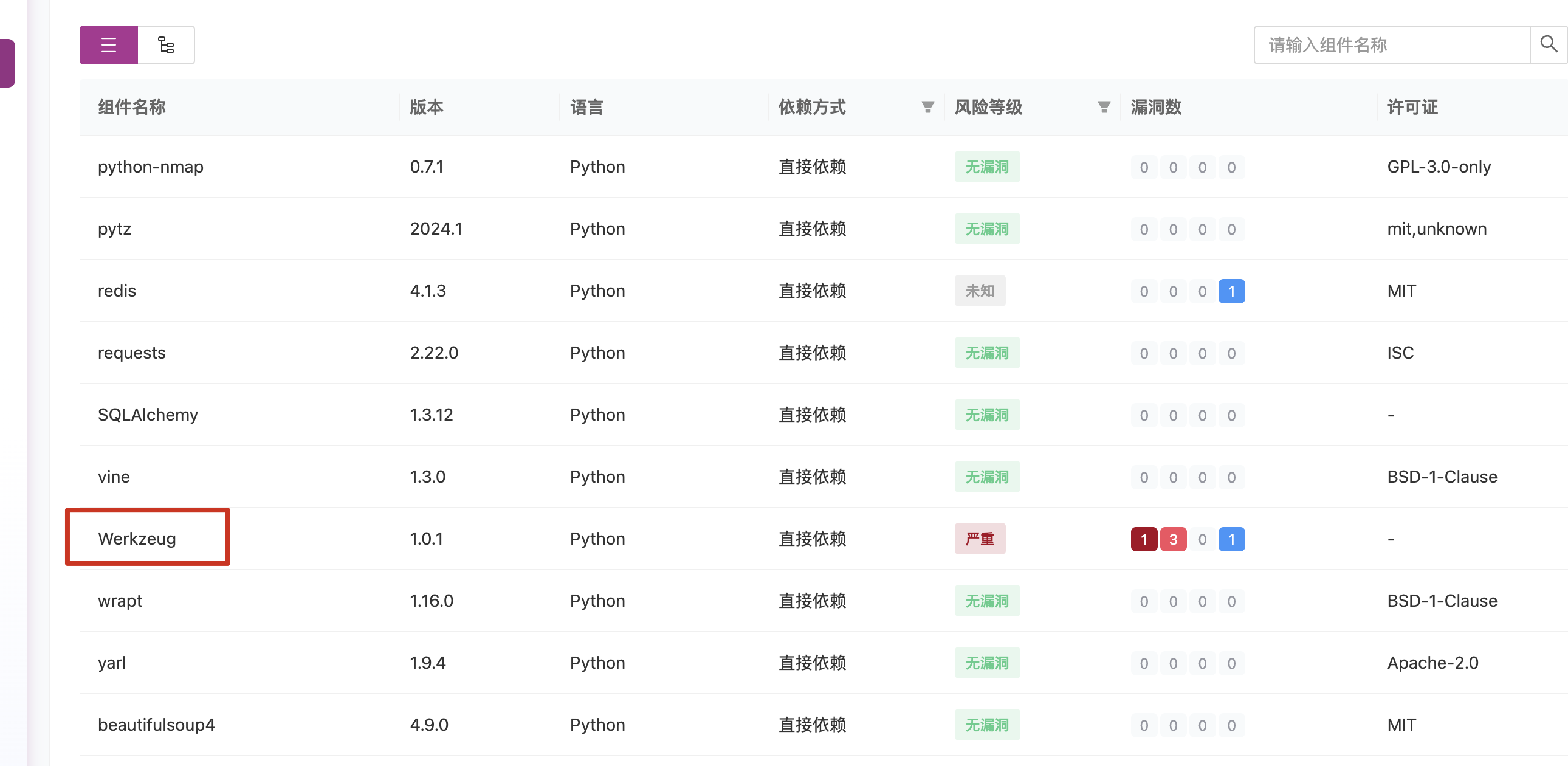
甲方安全建设之研发安全-SCA
前言 大多数企业或多或少的会去采购第三方软件,或者研发同学在开发代码时,可能会去使用一些好用的软件包或者依赖包,但是如果这些包中存在恶意代码,又或者在安装包时不小心打错了字母安装了错误的软件包,则可能出现供…...

[html]网页结构以及常见标签用法
哎,我服了,明明之前学了html的,但时间一长我就忘记了,本来flask学到视图了,但涉及到了html我觉得还是需要重新回顾一下,,,,,, web开发技术栈一共有3门语言。分别是: HTML:译作超文本标记语言&am…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
