重温数据结构与算法之深度优先搜索
文章目录
- 前言
- 一、实现
- 1.1 递归实现
- 1.2 栈实现
- 1.3 两者区别
- 二、LeetCode 实战
- 2.1 二叉树的前序遍历
- 2.2 岛屿数量
- 2.3 统计封闭岛屿的数目
- 2.4 从先序遍历还原二叉树
- 参考
前言
深度优先搜索(Depth First Search,DFS)是一种遍历或搜索树或图数据结构的算法。该算法从根节点开始(在图的情况下,选择一些任意的节点作为根节点),并在回溯之前尽可能地沿着每个分支进行探索。需要额外的内存,通常是一个堆栈,来跟踪到目前为止沿着指定分支发现的节点,这有助于回溯。
深度优先搜索算法的特点:
- 从一个起始节点开始,沿着一条路径不断访问邻接节点,直到没有未访问的邻接节点为止,然后回溯到上一个节点,继续访问其他邻接节点。
- 利用栈或递归来实现。
- 可以产生目标图的相应拓扑排序表。
深度优先搜索算法的优点:
- 简单易实现。
- 占用空间少。
- 可以找到从起始节点到任意可达节点的路径。
深度优先搜索算法的缺点:
- 不一定能找到最短路径或最优解。
- 可能会陷入死循环或无限递归。
深度优先搜索算法的应用场景:
- 拓扑排序 (课程安排、工程进度、依赖关系)
- 模拟游戏(如象棋、迷宫等)
- 连通性检测(如判断图中是否有环等)
- 旅行商问题(如求解最短路径等)
- 括号匹配(如检查表达式中的括号是否匹配等)
- 二叉树、线段树、红黑树、图等数据结构的遍历
在本文中,我们将介绍深度优先搜索算法的基本原理和实现方法,并通过一些例题来展示其应用。
一、实现
1.1 递归实现
从一个起始节点开始,沿着一条路径不断访问邻接节点,直到没有未访问的邻接节点为止,然后回溯到上一个节点,继续访问其他邻接节点,直到所有节点都被访问过为止。
示例代码如下:
public void dfs(int start) {visited[start] = true; //将起始节点标记为已访问for (int i = 0; i < n; i++) { //遍历邻接矩阵中start所在行if (matrix[start][i] == 1 && !visited[i]) { //如果存在边且未被访问过dfs(i); //递归调用dfs方法,以该节点为新起点进行遍历}}
}
1.2 栈实现
从一个起始节点开始,将其压入栈中,然后重复以下步骤:弹出栈顶元素,并将其标记为已访问;将该元素的所有未访问的邻接节点压入栈中。直到栈为空为止
示例代码如下:
public void dfs(int start) {Stack<Integer> stack = new Stack<>(); //创建栈对象stack.push(start); //起始节点入栈Set<Integer> visited = new HashSet<>(); //创建集合对象visited.add(start); //起始节点加入集合while (!stack.isEmpty()) { //只要栈不为空就继续循环int cur = stack.peek(); //获取栈顶元素但不出栈boolean flag = false; //设置标志位,表示是否有未访问过的邻接节点for (int i = 0; i < n; i++) { //遍历邻接矩阵中cur所在行if (matrix[cur][i] == 1 && !visited.contains(i)) { //如果存在边且未被访问过stack.push(i); //将该节点入栈visited.add(i); //将该节点加入集合System.out.print(i + " "); //打印该节点flag = true; //修改标志位为true,表示有未访问过的邻接节点break; //跳出循环,以该节点为新起点进行遍历}}if (!flag) { //如果没有未访问过的邻接节点,则说明已经到达最深处,需要回溯上一层继续遍历其他分支路径。stack.pop(); //将栈顶元素出栈 }}
}
下面是一个dfs搜索的动图
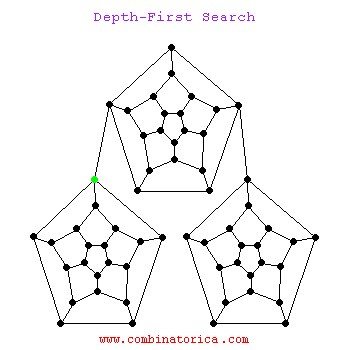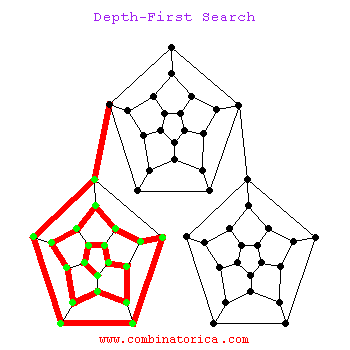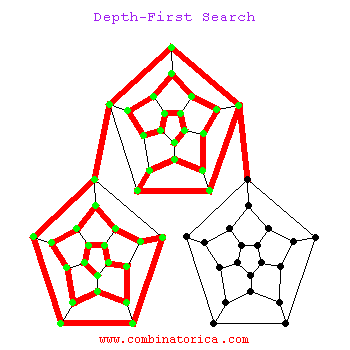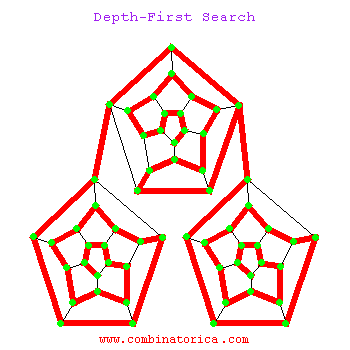
1.3 两者区别
- 递归实现是利用系统栈来保存当前节点的状态,当遇到死路时,自动回溯到上一个节点继续搜索。而栈实现是利用自定义的栈来保存当前节点的状态,当遇到死路时,手动弹出栈顶元素回溯到上一个节点继续搜索。
- 递归实现比较简洁易懂,但是效率不高,而且对于规模较大的图可能会导致栈溢出。而栈实现比较复杂一些,但是效率更高,而且可以避免栈溢出的问题。
- 递归实现和栈实现都需要一个标志数组来记录哪些节点已经被访问过,以防止重复访问或者陷入环路。
二、LeetCode 实战
2.1 二叉树的前序遍历
94. 二叉树的前序遍历
给你二叉树的根节点
root,返回它节点值的 前序 遍历。
List<Integer> ans = new ArrayList(); //定义一个整数列表,用来存储前序遍历的结果
public List<Integer> preorderTraversal(TreeNode root) {if (root != null) { //如果当前节点不为空,才进行以下操作ans.add(root.val); //把当前节点的值加入列表preorderTraversal(root.left); //递归地对左子树进行前序遍历preorderTraversal(root.right); //递归地对右子树进行前序遍历}return ans; //返回前序遍历的结果
}
2.2 岛屿数量
200. 岛屿数量
给你一个由
'1'(陆地)和'0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
// 定义一个二维数组pos,表示四个方向
int[][] pos = { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };
// 定义一个变量ans,表示岛屿的数量
int ans = 0;// 定义一个方法numIslands,接受一个二维字符数组grid作为参数,返回岛屿的数量
public int numIslands(char[][] grid) {// 获取grid的行数和列数int m = grid.length, n = grid[0].length;// 定义一个二维布尔数组visited,表示每个位置是否被访问过boolean[][] visited = new boolean[m][n];// 遍历grid中的每个位置for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {// 如果当前位置是'1'且没有被访问过,则从该位置开始深度优先搜索,并将ans加一if (grid[i][j] == '1' && !visited[i][j]) {dfs(grid, visited, i, j);ans++;}}}// 返回ans作为结果return ans;
}// 定义一个方法dfs,接受一个二维字符数组grid、一个二维布尔数组visited、两个整数i和j作为参数,无返回值
public void dfs(char[][] grid, boolean[][] visited, int i, int j) {// 如果i或j越界或者当前位置是'0'或者已经被访问过,则直接返回if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == '0'|| visited[i][j]) {return;}// 将当前位置标记为已访问visited[i][j] = true;// 遍历四个方向,并递归调用dfs方法for (int[] p : pos) {dfs(grid, visited, i + p[0], j + p[1]);}}
2.3 统计封闭岛屿的数目
1254. 统计封闭岛屿的数目
二维矩阵
grid由0(土地)和1(水)组成。岛是由最大的4个方向连通的0组成的群,封闭岛是一个完全由1包围(左、上、右、下)的岛。请返回 封闭岛屿 的数目。
// 定义一个二维数组pos来存储上下左右四个方向的偏移量
int[][] pos = { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };
// 定义一个变量ans来记录封闭岛屿的个数
int ans = 0;public int closedIsland(int[][] grid) {// 判断矩阵是否为空,如果为空,直接返回0if (grid == null || grid.length == 0 || grid[0].length == 0) {return 0;}// 获取矩阵的行数和列数int m = grid.length, n = grid[0].length;// 遍历矩阵中的每一个元素for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {// 如果当前元素是岛屿(0),则调用dfs函数来检查它是否被水域(1)完全包围if (grid[i][j] == 0 && dfs(grid, i, j)) {// 如果dfs函数返回true,说明当前岛屿是封闭的,ans加一ans++;}}}// 返回ans作为最终答案return ans;
}
public boolean dfs(int [][] grid, int i, int j) {// 如果当前坐标超出了矩阵的边界,说明当前岛屿不是封闭的,返回falseif (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length) {return false;}// 如果当前元素是水域(1),说明没有遇到边界,返回trueif (grid[i][j] == 1) {return true;}// 将当前元素标记为水域(1),避免重复访问grid[i][j] = 1;// 使用一个for循环来遍历上下左右四个方向,并将结果进行逻辑与运算boolean res = true;for (int [] p: pos) {res &= dfs(grid, i + p[0], j + p[1]);}// 返回res作为dfs函数的结果return res;
}
2.4 从先序遍历还原二叉树
1028. 从先序遍历还原二叉树
我们从二叉树的根节点
root开始进行深度优先搜索。在遍历中的每个节点处,我们输出
D条短划线(其中D是该节点的深度),然后输出该节点的值。(如果节点的深度为D,则其直接子节点的深度为D + 1。根节点的深度为0)。如果节点只有一个子节点,那么保证该子节点为左子节点。
给出遍历输出
S,还原树并返回其根节点root。
int index = 0; // 定义全局变量indexpublic TreeNode recoverFromPreorder(String traversal) {int[] deep = Arrays.stream(traversal.split("[0-9]{1,10}")).mapToInt(String::length).toArray(); // 将输入字符串按照数字分割成数组deepint[] number = Arrays.stream(traversal.split("-{1,100}")).mapToInt(Integer::parseInt).toArray(); // 将输入字符串按照连字符分割成数组numberif (deep.length == 0) deep = new int[]{0}; // 如果deep为空,则赋值为[0]return dfs(deep, number); // 调用dfs函数并返回结果
}public TreeNode dfs(int [] deep, int [] number) {TreeNode treeNode = new TreeNode(number[index]); // 创建新的TreeNode对象并赋值int curHeight = deep[index]; // 获取当前节点的深度if (index + 1 < deep.length && curHeight == deep[index + 1] - 1) { // 判断是否有左子节点index++; // 将index加1treeNode.left = dfs(deep, number); // 递归调用dfs并赋值给左子节点}if (index + 1 < deep.length && curHeight == deep[index + 1] - 1) { // 判断是否有右子节点index++; // 将index加1treeNode.right = dfs(deep, number); // 递归调用dfs并赋值给右子节点}return treeNode; // 返回当前节点
}
参考
- https://en.wikipedia.org/wiki/Depth-first_search
- https://zh.wikipedia.org/wiki/深度优先搜索
- 深度优先搜索 —— 新手上路的一道坎
相关文章:

重温数据结构与算法之深度优先搜索
文章目录前言一、实现1.1 递归实现1.2 栈实现1.3 两者区别二、LeetCode 实战2.1 二叉树的前序遍历2.2 岛屿数量2.3 统计封闭岛屿的数目2.4 从先序遍历还原二叉树参考前言 深度优先搜索(Depth First Search,DFS)是一种遍历或搜索树或图数据结…...

STM32F103驱动LD3320语音识别模块
STM32F103驱动LD3320语音识别模块LD3320语音识别模块简介模块引脚定义STM32F103ZET6开发板与模块接线测试代码实验结果LD3320语音识别模块简介 基于 LD3320,可以在任何的电子产品中,甚至包括最简单的 51 作为主控芯片的系统中,轻松实现语音识…...

2023 最新可用Google镜像地址 长期更新
Google镜像说明 由于种种原因,国家还未开放Google搜索的使用。虽然可以通过某些技术手段实现访问,但是还是有一些同学需要借助Google搜索镜像才可以达到访问的目的;笔者特意搜集了一些2022年最新的Google搜索镜像供有需求的童鞋使用…...
及其算法变种(附matlab和python代码实现))
MATLAB算法实战应用案例精讲-【优化算法】蝗虫优化算法(GOA)及其算法变种(附matlab和python代码实现)
目录 前言 算法原理 算法思想 GOA 算法的数学模型 迭代模型 算法流程...

数据结构与算法 顺序表、链表总结
文章目录顺序表1、顺序表的基本概念链表1 简介链表概念链表特点链表与数组的对比2 链表的类型分类链表循环单向链表1 简介概念2 数据存储和实现数据存储数据实现3 操作基本操作实现线性表(List):零个或多个数据元素的有限序列。在较复杂的线性…...

Nginx集群搭建-三台
1.使用root用户登录Linux服务器 2.创建用户 输入 adduser test 后回车 #test 为创建的用户 3.为创建的用户设置密码 输入 passwd test 后回车 输入两次密码 4.出现 passwd:所有的身份验证令牌已经成功更新。证明Linux新用户和密码创建成功 5.使用新用户test登录Linu…...

【算法】图的存储和遍历
作者:指针不指南吗 专栏:算法篇 🐾或许会很慢,但是不可以停下🐾 文章目录1. 图的存储1.1 邻接矩阵1.2 邻接表2. 图的遍历2.1 dfs 遍历2.2 bfs 遍历1. 图的存储 引入 一般来说,树和图有两种存储方式&#…...
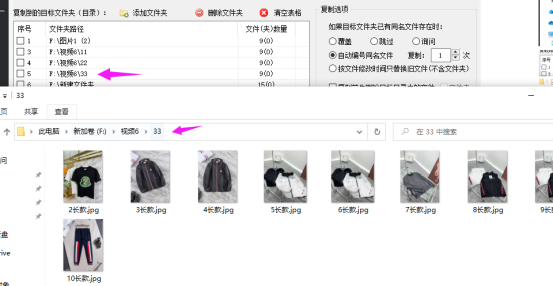
文件如何批量复制保存在多个文件夹中
在日常工作中经常需要整理文件,比如像文件或文件夹重命名或文件批量归类,文件批量复制到指定某个或多个文件来中保存备份起来。一般都家最常用方便是手动一个一个去重命名或复制到粘贴到某个文件夹中保存,有没有简单好用的办法呢,…...

16N60-ASEMI高压MOS管16N60
编辑-Z 16N60在TO-220封装里的静态漏极源导通电阻(RDS(ON))为0.2Ω,是一款N沟道高压MOS管。16N60的最大脉冲正向电流ISM为48A,零栅极电压漏极电流(IDSS)为10uA,其工作时耐温度范围为-55~150摄氏度。16N60功耗…...
)
Open3D 多个点云配准(C++版本)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 多路配准(多个点云配准)是指在全局空间中对齐多个几何块的过程。输入的数据可以是点云或深度图像 P i P_i P...

java实现Hbase 增删改查
目录 一、新建一个maven工程 二、代码实现 2.1、配置hbase信息,连接hbase数据库 2.2、创建命名空间 2.3、创建表 2.4、删除表,删除之前要设置为禁用状态 2.5、添加数据 2.6、获取命令表空间 / tables列表 2.7、get方法查看表的内容 2.8、scan方法…...

1109. 航班预订统计 差分数组
1109. 航班预订统计 差分数组技巧适⽤于频繁对数组区间进⾏增减的场景 1.由数组a生成差分数组b{b[0]0,i0(或者b[0]a[0],i0)b[i]a[i]−a[i−1],i>01.由数组a生成差分数组b\left\{\begin{array}{l}b[0]0,i0(或者b[0]a[0],i0)\\ b[i]a[i]-a[i-1],i>0\end{array}\right. 1.由…...

图床搭建,使用typora上传
1. 准备gitee作为图床的仓库 新建仓库 准备仓库的私人令牌,后面配合使用 点击个人设置——》私人令牌 注意私人令牌,复制保存好,后面不能再看了 2. 准备PicGO,并进行相关配置 PicGo官方下载链接 下载安装好node.js,下载网址 安…...
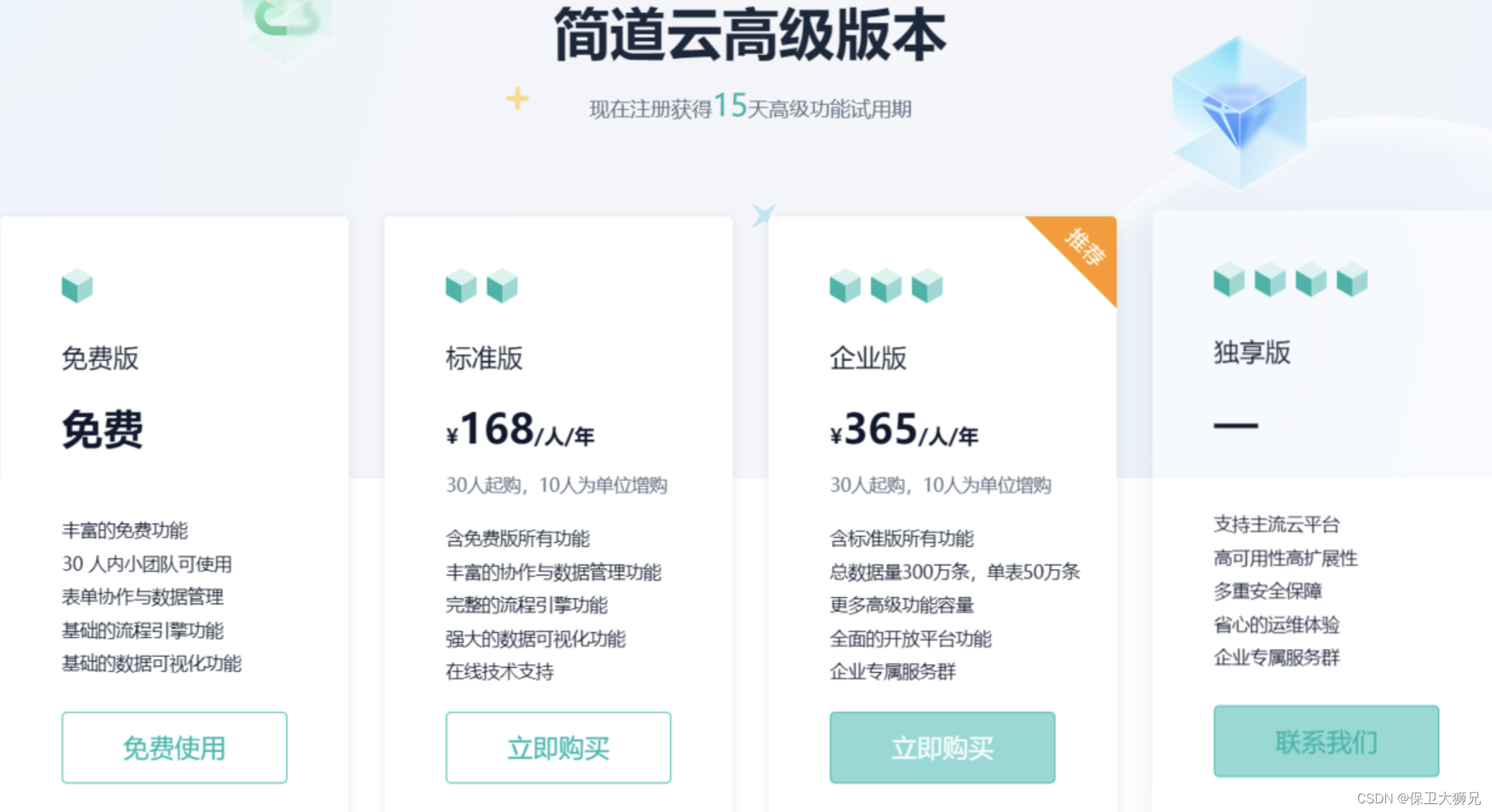
低代码开发的优势是什么?
低代码开发的优势是什么?低代码开发这个概念这两年来经常出现在人们的视野中,市场对于低代码的需求也越来越庞大。 Gartner预测,到2025年,75%的大型企业将使用至少四种低代码/无代码开发工具,用于IT应用开发和公民开发计划。 可…...

Ip2Resion线上部署报数据越界及错误处理
上篇在本地测试调用Ip2Resigon解析行政区划 Ip2Region的Java本地实现运行正常,但部署到测试环境,抛出数组越界(java.lang.ArrayIndexOutOfBoundsException)异常。 环境信息 ip2Resion是2.7版本,对应文件后缀为 xdb。 …...

致敬我的C++启蒙老师,跟着他学计算机编程就对了 (文末赠书5本)
致敬我的C启蒙老师,跟着他学计算机编程就对了 摘要 讲述了一个故事,介绍了一位良师,一段因C而续写的回忆,希望对各位看官有所帮助和启发。 文章目录1 写在前面2 我的C启蒙老师3 谈谈老师给我的启发4 友情推荐5 文末福利1 写在前面…...

CSS中的伪元素和伪类
一直被伪类和伪元素所迷惑,以为是同一个属性名称,根据CSS动画,索性开始研究a:hover:after,a.hover:after的用法。 伪元素 是HTML中并不存在的元素,用于将特殊的效果添加到某些选择器。 对伪元素的描述 伪元素有两…...

逻辑优化基础-rewrite
简介 逻辑综合中的rewrite算法是一种常见的优化算法,其主要作用是通过对逻辑电路的布尔函数进行等效变换,从而达到优化电路面积、时序和功耗等目的。本文将对rewrite算法进行详细介绍,并附带Verilog代码示例。 一、算法原理 rewrite算法的…...
案例27-单表从9个更新语句调整为2个
目录 一:背景介绍 二:思路&方案 三:过程 1.项目结构 2.准备一个普通的maven项目,部署好mysql数据库 3.在项目中引入pom依赖 5.编写MyBitis配置文件 6.编写Mysql配置类 7.编写通用Update语句 8.项目启动类 四:总…...

Wordpress paid-memberships-pro plugins CVE-2023-23488未授权SQLi漏洞分析
目录 1.漏洞概述 2.漏洞等级 3.调试环境 4.漏洞代码 5 POC 1.漏洞概述 WordPress插件paid-memberships-pro版本<2.9.8中,容易受到REST路由“/pmpro/v1/order”的“code”参数中未验证的SQL注入漏洞的影响。攻击者可进行SQLi盲注,从而获取数据库权限。 CVE:...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
