LeetCode-1766. 互质树【树 深度优先搜索 广度优先搜索 数组 数学 数论】
LeetCode-1766. 互质树【树 深度优先搜索 广度优先搜索 数组 数学 数论】
- 题目描述:
- 解题思路一:DFS 中记录节点值的深度和编号,回溯写法。关键点是1 <= nums[i] <= 50
- 解题思路二:0
- 解题思路三:0
题目描述:
给你一个 n 个节点的树(也就是一个无环连通无向图),节点编号从 0 到 n - 1 ,且恰好有 n - 1 条边,每个节点有一个值。树的 根节点 为 0 号点。
给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i] 表示第 i 个点的值,edges[j] = [uj, vj] 表示节点 uj 和节点 vj 在树中有一条边。
当 gcd(x, y) == 1 ,我们称两个数 x 和 y 是 互质的 ,其中 gcd(x, y) 是 x 和 y 的 最大公约数 。
从节点 i 到 根 最短路径上的点都是节点 i 的祖先节点。一个节点 不是 它自己的祖先节点。
请你返回一个大小为 n 的数组 ans ,其中 ans[i]是离节点 i 最近的祖先节点且满足 nums[i] 和 nums[ans[i]] 是 互质的 ,如果不存在这样的祖先节点,ans[i] 为 -1 。
示例 1:
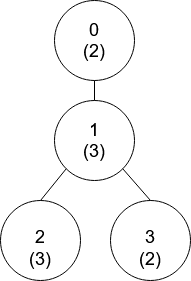
输入:nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
输出:[-1,0,0,1]
解释:上图中,每个节点的值在括号中表示。
- 节点 0 没有互质祖先。
- 节点 1 只有一个祖先节点 0 。它们的值是互质的(gcd(2,3) == 1)。
- 节点 2 有两个祖先节点,分别是节点 1 和节点 0 。节点 1 的值与它的值不是互质的(gcd(3,3) == 3)但节点 0 的值是互质的(gcd(2,3) == 1),所以节点 0 是最近的符合要求的祖先节点。
- 节点 3 有两个祖先节点,分别是节点 1 和节点 0 。它与节点 1 互质(gcd(3,2) == 1),所以节点 1 是离它最近的符合要求的祖先节点。
示例 2:
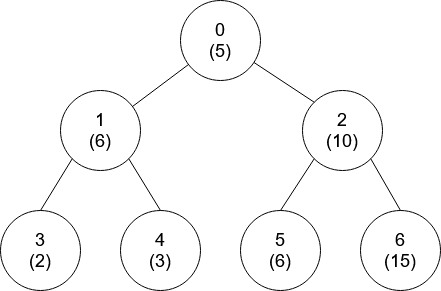
输入:nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
输出:[-1,0,-1,0,0,0,-1]
提示:
nums.length == n
1 <= nums[i] <= 50
1 <= n <= 105
edges.length == n - 1
edges[j].length == 2
0 <= uj, vj < n
uj != vj
解题思路一:DFS 中记录节点值的深度和编号,回溯写法。关键点是1 <= nums[i] <= 50
对于节点 x,我们需要计算节点值与 nums[x] 互质的最近祖先节点是哪个。
最暴力的做法是,枚举 x 的所有祖先节点。但如果这棵树是一条链,枚举 x 的所有祖先节点需要 O(n) 的时间,每个点都这样枚举的话,总共需要 O(n2) 的时间,太慢了。
注意到,所有节点的节点值都不超过 50,我们可以枚举 [1,50] 中与 nums[x] 互质的数。由于要计算的是「最近」祖先,对于节点值相同的祖先,只需枚举深度最大的。因此,对于节点 x,我们至多枚举它的 50 个祖先。这样总共只需要 O(nU) 的时间,其中 U=50。
具体来说,我们需要在递归这棵树的同时,维护两组信息:
- valDepth 数组。其中 valDepth[j] 保存节点值等于 j 的最近祖先的深度。
- valNodeId 数组。其中 valNodeId[j] 保存节点值等于 j 的最近祖先的节点编号。
设当前节点值为 val=nums[x],我们枚举 [1,50] 中与 val互质的数字 j,计算出 valDepth[j] 的最大值,及其对应的节点编号,即为答案 ans[x]。
代码实现时,可以预处理 [1,50]中有哪些数对是互质的。
# 预处理:coprime[i] 保存 [1, MX) 中与 i 互质的所有元素
MX = 51
coprime = [[j for j in range(1, MX) if gcd(i, j) == 1]for i in range(MX)]
class Solution:def getCoprimes(self, nums: List[int], edges: List[List[int]]) -> List[int]:n = len(nums)g = [[] for _ in range(n)]for x, y in edges:g[x].append(y)g[y].append(x)ans = [0] * nval_depth_id = [(-1, -1)] * MX # 包含深度和节点编号def dfs(x: int, fa: int, depth: int) -> None:val = nums[x] # x 的节点值# 计算与 val 互质的祖先节点值中,节点深度最大的节点编号ans[x] = max(val_depth_id[j] for j in coprime[val])[1]tmp = val_depth_id[val] # 用于恢复现场val_depth_id[val] = (depth, x) # 保存 val 对应的节点深度和节点编号for y in g[x]:if y != fa:dfs(y, x, depth + 1)val_depth_id[val] = tmp # 恢复现场dfs(0, -1, 0)return ans
时间复杂度:O(n)
空间复杂度:O(n)
解题思路二:0
时间复杂度:O(n)
空间复杂度:O(n)
解题思路三:0
时间复杂度:O(n)
空间复杂度:O(n)
相关文章:

LeetCode-1766. 互质树【树 深度优先搜索 广度优先搜索 数组 数学 数论】
LeetCode-1766. 互质树【树 深度优先搜索 广度优先搜索 数组 数学 数论】 题目描述:解题思路一:DFS 中记录节点值的深度和编号,回溯写法。关键点是1 < nums[i] < 50解题思路二:0解题思路三:0 题目描述࿱…...

“数据安全服务能力”评定资格认证!不容错过
数据安全服务能力评定是指对数据安全服务提供商从事数据安全服务综合能力的评定,包括技术能力、服务能力、质量保证能力、人员构成与素质、经营业绩、资产状况等要素。 一、能力评定类型与等级 数据安全服务能力分为二个类型:数据安全评估、数据安全建…...

【MATLAB 分类算法教程】_3麻雀搜索算法优化支持向量机SVM分类 - 教程和对应MATLAB代码
分类代码案例3:麻雀搜索算法优化支持向量机SVM分类 - MATLAB完全代码教程 1. 初始化代码2.读取数据代码3.数据预处理代码4.利用麻雀搜索算法SSA求解最佳的SVM参数c和g代码5.根据最佳的参数进行SVM模型训练代码6.SVM模型预测代码7.准确率分析以及分类结果对比作图代码本文以红酒…...

利用机器学习库做动态定价策略的例子
动态定价是一个复杂的问题,涉及到市场需求、库存、竞争对手行为、季节性因素等多个变量。在实际应用中,动态定价通常需要复杂的模型和大量的数据分析。我选择使用Python(Golearn库)进行机器学习模型的训练和部署,而将G…...
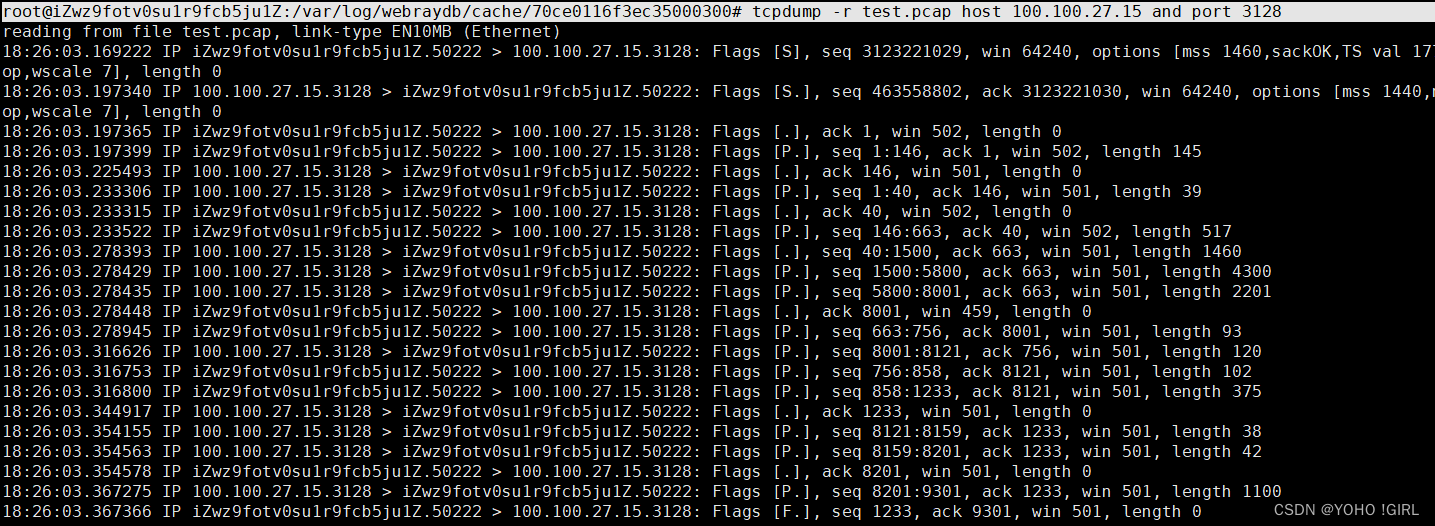
Tcpdump -r 解析pcap文件
当我们使用命令抓包后,想在命令行直接读取筛选怎么办?-r参数就支持了这个 当你使用 tcpdump 的 -r 选项读取一个之前捕获的数据包文件,并想要筛选指定 IP 地址和端口的包时,你可以在命令中直接加入过滤表达式。这些过滤表达式可以…...
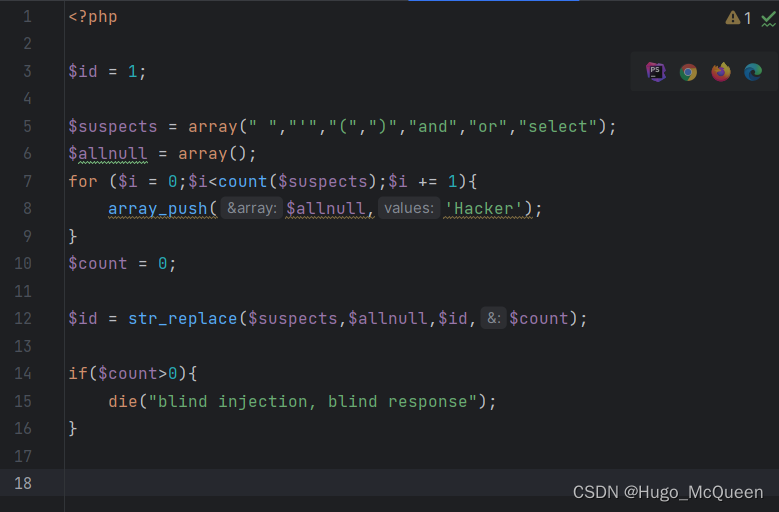
[dvwa] sql injection(Blind)
blind 0x01 low 1’ and length(version()) 6 # syntax: substr(string , from<start from 1>, cut length) 1’ and substr(version(),1,1) ‘5’ # 1’ and substr(version(),2,1) ‘.’ # 1’ and substr(version(),3,1) ‘7’ # 1’ and substr(version(),4,…...
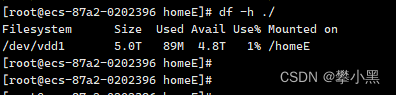
linux 挂载云盘 NT只能挂载2T,使用parted挂载超过2T云盘
一、删除原来挂载好的云盘和分区 1、查看挂载号的云盘 fdisk -l 发现我们有5千多G但是只挂载了2T,心里非常的慌张!十分的不爽! 好,我们把它干掉,重新分区! 2、解除挂载 umount /homeE 没保存跳转到&…...
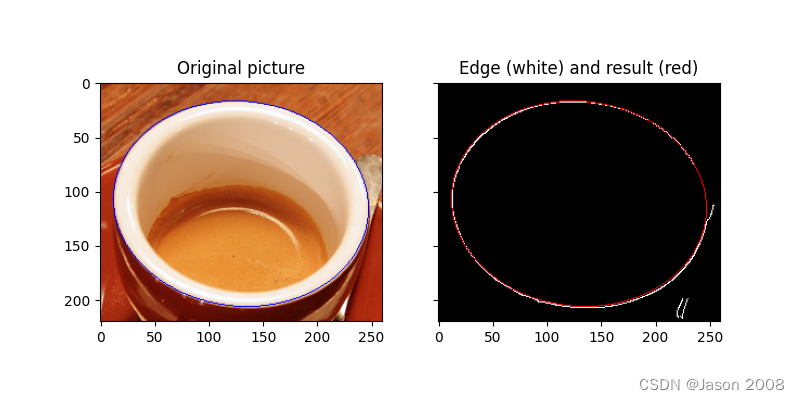
用Skimage学习数字图像处理(021):图像特征提取之线检测(下)
本节是特征提取之线检测的下篇,讨论基于Hough变换的线检测方法。首先简要介绍Hough变换的基本原理,然后重点介绍Skimage中含有的基于Hough变换的直线和圆形检测到实现。 目录 10.4 Hough变换 10.4.1 原理 10.4.2 实现 10.4 Hough变换 Hough变换&…...

ArduPilot飞控之Gazebo + SITL + MP的Jetson Orin环境搭建
ArduPilot飞控之Gazebo SITL MP的Jetson Orin环境搭建 1. 源由2. Linux环境整理3. 安装Gazebo环境3.1 安装Gazebo3.2 安装插件3.3 配置插件3.4 测试Gazebo 4. 安装Arudpilot-SITL环境4.1 克隆工程4.2 编译准备4.3 环境配置4.4 配置编译4.5 测试运行 5. 测试运行6. 参考资料 1…...

前端错误监控的方法有哪些
前端错误监控是指通过各种手段收集、分析和处理前端应用运行中发生的错误 常用的前端错误监控的方法有 使用 try catch 方法 捕获特定代码块中的错误多用于处理特定函数或代码段可能抛出的异常,尤其是异步代码网络请求错误监控 promise.catchtry catch全局错误处理…...

✌粤嵌—2024/3/11—跳跃游戏
代码实现: 方法一:递归记忆化 int path; int used[10000];bool dfs(int *nums, int numsSize) {if (path numsSize - 1) {return true;}for (int i 1; i < nums[path]; i) {if (used[path i]) {continue;}path i;used[path] 1;if (dfs(nums, num…...
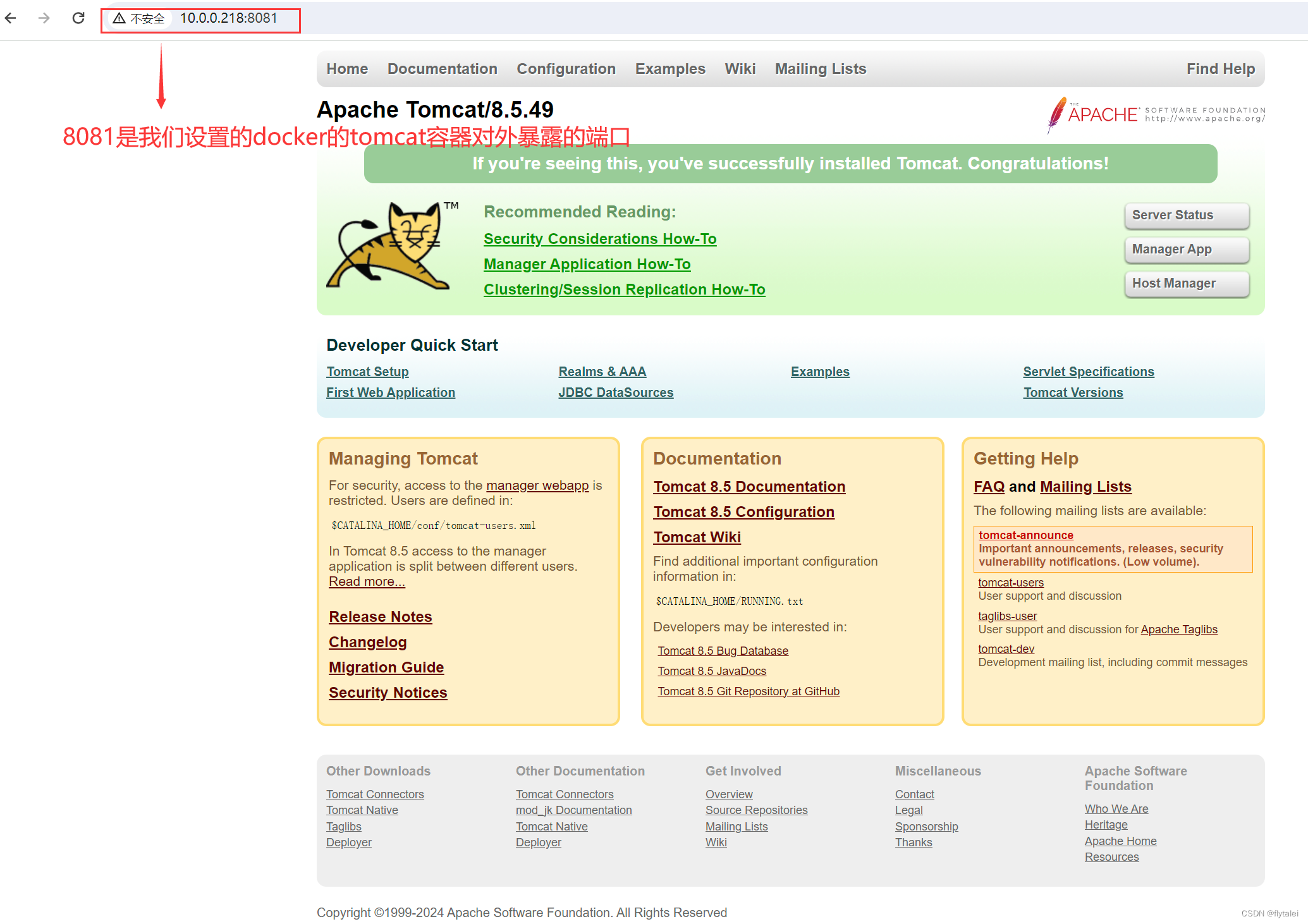
Docker入门实战教程
文章目录 Docker引擎的安装Docker比vm虚拟机快 Docker常用命令帮助启动类命令镜像命令docker imagesdocker searchdocker pulldocker system dfdocker rmi 容器命令redis前台交互式启动redis后台守护式启动Nginx容器运行ubuntu交互式运行tomcat交互式运行对外暴露访问端口 Dock…...

数据结构初阶:二叉树(一)
树概念及结构 树的概念 树是一种 非线性 的数据结构,它是由 n ( n>0 )个有限结点组成一个具有层次关系的集合。 把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 。 有一个特殊的结点&a…...
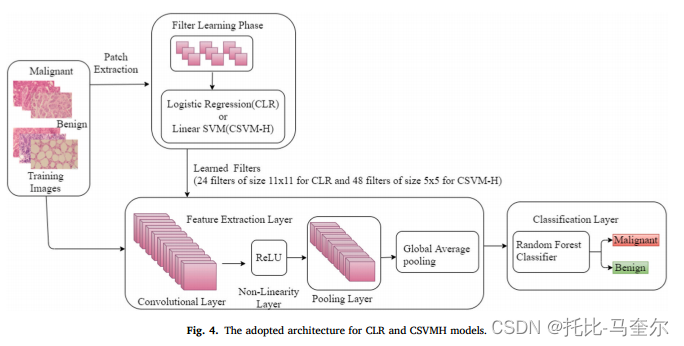
基于逻辑回归和支持向量机的前馈网络进行乳腺癌组织病理学图像分类
CNN(卷积神经网络)通过使用反向传播方法来学习特征,这种方法需要大量的训练数据,并且存在梯度消失问题,从而恶化了特征学习。 CNN卷积神经网络 CNN由一个多层神经网络组成,该网络从标记的训练数据集中学习…...

35-4 fastjson漏洞复现
环境准备:35-2 fastjson反序列化漏洞介绍 及漏洞环境搭建-CSDN博客 fastjson_tool.jar下载:fastjson_rce_tool: fastjson命令执行自动化利用工具, remote code execute,JNDI服务利用工具 RMI/LDAP (gitee.com) 一、攻击机kali开启nc监听6666端口(或其他端口也行,只要不…...

Qt-控件篇
QPushbutton 1、设置按钮文本 pushButton->setText("按钮"); 2、获取按钮文本 pushButton->text(); 3、设置按钮的大小为特定值(宽度和高度) pushButton->setFixedSize(width,height); 4、设置按钮悬停时的工具提示文本。 pushButto…...

实现 Table 的增加和删除,不依赖后端数据回显
需求 删除前 删除后 分析 首先写一个 Table <a-card style"width:100%"><template#extra><a-button type"text" click"addSelectItem" style"margin-right: 5px">添加</a-button><a-button type&quo…...
——三系统后端nodejs+express)
个人网站开发记录(七)——三系统后端nodejs+express
前言 这种已经完全工程化了的()后端其实已经没啥好说的了,因为就是单纯的写接口然后调用接口就完事了! 正文 唯一值得一提的大概是我在写这个系统的时候搞了https的链接,具体来说就是先申请一个ssl证书,…...

C#入门理解设计模式的6大原则
**设计模式的原则是指导设计模式创建和应用的基本原则,这些原则有助于创建灵活、可维护且可扩展的软件系统。**1. 单一职责原则(Single Responsibility Principle, SRP) 单一职责原则指出一个类应该只有一个引起它变化的原因。换句话说&…...

Linux如何切换root用户
Linux如何切换root用户 sudosudo -i想一直使用root权限,可以使用su命令 sudo 执行命令后,输入用户密码可以短暂的获取root权限 sudo -i 通过此命令直接输入当前管理员用户的密码就可以进入root用户了 想一直使用root权限,可以使用su命令 …...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...

第14节 Node.js 全局对象
JavaScript 中有一个特殊的对象,称为全局对象(Global Object),它及其所有属性都可以在程序的任何地方访问,即全局变量。 在浏览器 JavaScript 中,通常 window 是全局对象, 而 Node.js 中的全局…...

宠物车载安全座椅市场报告:解读行业趋势与投资前景
一、什么是宠物车载安全座椅? 宠物车载安全座椅是一种专为宠物设计的车内固定装置,旨在保障宠物在乘车过程中的安全性与舒适性。它通常由高强度材料制成,具备良好的缓冲性能,并可通过安全带或ISOFIX接口固定于车内。 近年来&…...
