C语言每日一练(12、水仙花数)
在编程的领域中,我们常常会遇到一些有趣而富有挑战性的问题。今天,让我们一起来探讨一个经典的编程题目——打印出所有的“水仙花数”。
所谓“水仙花数”,是指一个三位数,其各位数字的立方和等于该数本身。例如,153 就是一个典型的“水仙花数”,因为 153 等于 1 的三次方加上 5 的三次方再加上 3 的三次方。
以下是用 C 语言实现找出所有“水仙花数”的代码及详细注释:
#include <stdio.h>main()
{int i,j,k,n; // 定义变量,i 表示百位,j 表示十位,k 表示个位,n 用于遍历 100 到 999 的数printf("'water flower'number is:");for(n=100;n<1000;n++) // 从 100 开始到 999 进行循环{i=n/100; /* 利用除法运算分解出百位 */j=n/10%10; /* 先除以 10 得到百位和十位,再取余 10 得到十位 */k=n%10; /* 利用取模运算分解出个位 */if(i*100+j*10+k==i*i*i+j*j*j+k*k*k) // 判断是否满足水仙花数的条件{printf("%-5d",n); // 打印出满足条件的水仙花数}}printf("\n");
}以下是一种快速判断一个数是否为水仙花数的方法步骤:
- 将这个数转换为字符串,以便获取各个数位上的数字。
- 提取出每个数位上的数字。
- 将这些数字进行立方计算。
- 将立方后的结果相加。
- 判断相加的结果是否等于原数,如果等于则是水仙花数,否则不是。
例如,对于数字 153,先转换为字符串"153",然后提取出 1、5、3,计算 1³、5³、3³ 并相加得到 153,与原数相等,所以 153 是水仙花数。
通过这段代码,我们可以清晰地看到如何通过逐步分析每个三位数的各个数位,并进行条件判断,从而找出那些神奇的“水仙花数”。这不仅是对编程技巧的一种锻炼,也是对数学与计算机科学奇妙结合的一次体验。希望大家在这个过程中也能感受到编程带来的乐趣和挑战!
让我们一起在编程的海洋中继续探索更多的精彩吧!
相关文章:
)
C语言每日一练(12、水仙花数)
在编程的领域中,我们常常会遇到一些有趣而富有挑战性的问题。今天,让我们一起来探讨一个经典的编程题目——打印出所有的“水仙花数”。 所谓“水仙花数”,是指一个三位数,其各位数字的立方和等于该数本身。例如,153 …...

HTML5实现酷炫个人产品推广、工具推广、信息推广、个人主页、个人介绍、酷炫官网、门户网站模板源码
文章目录 1.设计来源1.1 主界面1.2 我的产品界面1.3 关于我们界面1.4 照片墙界面1.5 发展历程界面1.6 优秀人才界面1.7 热门产品界面1.8 联系我们界面 2.灵活调整模块3.效果和源码3.1 动态效果3.2 源代码 源码下载 作者:xcLeigh 文章地址:https://blog.c…...

系统如何做好安全加固?
一、Windows系统 Windows系统出厂时,微软为了兼容性,默认并未对系统安全做严格的限制,因此还需要做一些基本的安全加固,方可防止黑客入侵。 1、系统补丁更新 为什么要更新系统补丁?很多人感觉漏洞更新没必要&#x…...

对NI系统和PLC系统的应用比较
以下是对这两种系统的基本比较: 1. 设计和功能性 NI系统: 通常基于LabVIEW等软件平台,提供强大的数据采集、信号处理和图形界面开发能力。高度模块化和可扩展,支持各种传感器和信号类型。适合进行复杂的数据分析和高级控制算法的…...
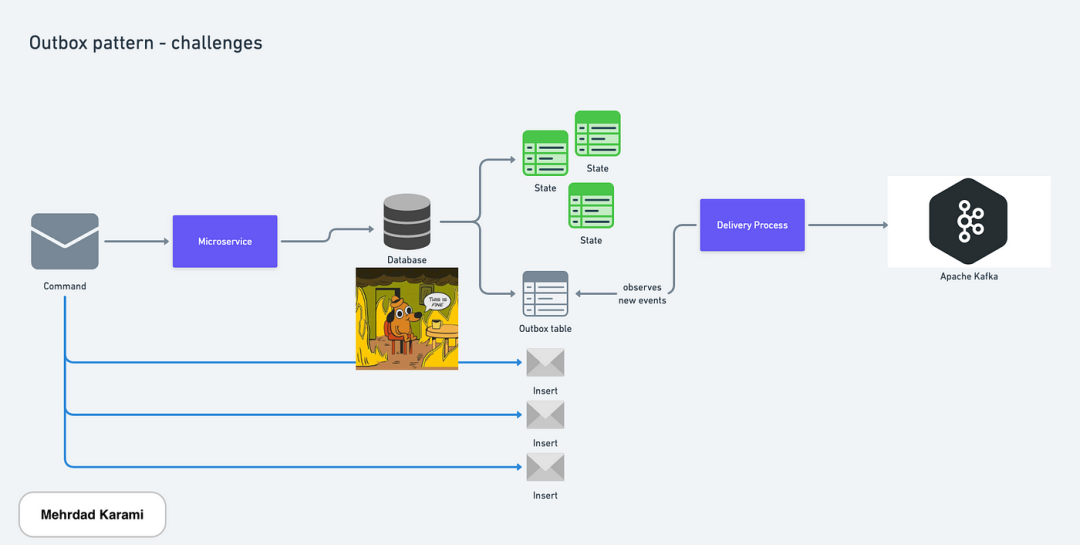
微服务架构中的挑战及应对方式:Outbox 模式
使用 Outbox 模式保持微服务数据一致性 在一个由许多小型服务组成的系统中保持数据一致性是困难的,因为它们分散在各处。以下是一些常见问题以及如何处理它们的方法:当服务发送消息时,同时更新数据库和发送消息是棘手的问题。 在微服务中发出…...

使用Docker安装MySQL5.7.36
拉取镜像并查看 docker pull mysql:5.7.36拉取成功后查看(非必须) docker images创建并设置宿主机 mysql 配置文件目录和数据文件目录 创建相关文件夹将容器中的mysql数据保存到本地,这样即使容器被删除,数据也不会丢失。 mkd…...
)
【PyTorch】6-可视化(网络结构可视化、CNN可视化、TensorBoard、wandb)
PyTorch:6-可视化 注:所有资料来源且归属于thorough-pytorch(https://datawhalechina.github.io/thorough-pytorch/),下文仅为学习记录 6.1:可视化网络结构 Keras中可以调用model.summary()的API进行模型参数可视化 torchinfo…...

C++容器——map和pair对组
pair(对组) 是一种模板类,允许将两个不同类型的值组合在一起。它由两个数据成员first和second组成,分别用来保存这两个值。 头文件 加头文件 #include<utility> 对于 C11 及以上标准,pair 类型可以在不包含头…...
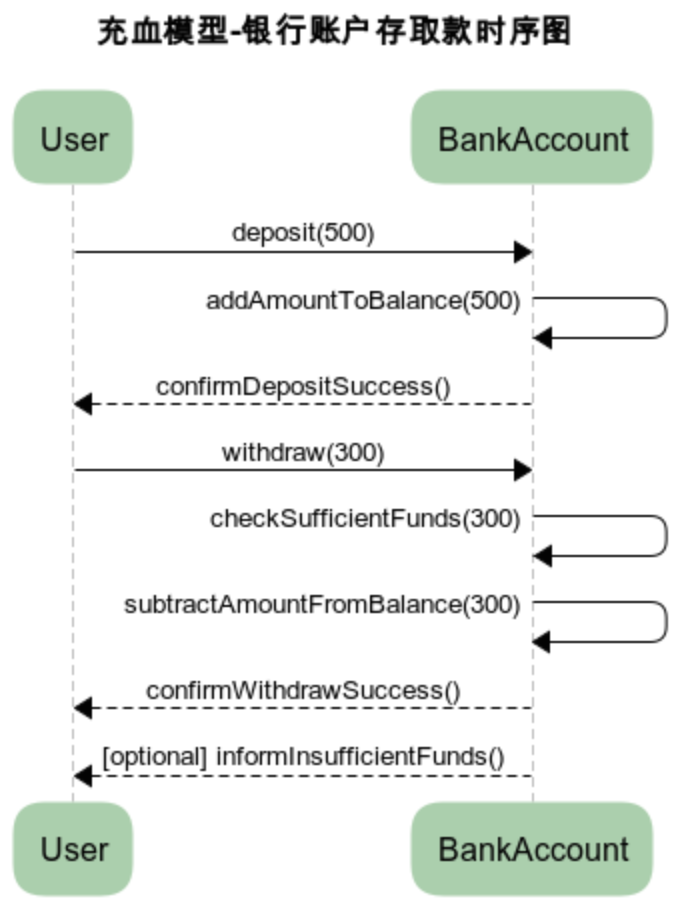
MVC和DDD的贫血和充血模型对比
文章目录 架构区别MVC三层架构DDD四层架构 贫血模型代码示例 充血模型代码示例 架构区别 MVC三层架构 MVC三层架构是软件工程中的一种设计模式,它将软件系统分为 模型(Model)、视图(View)和控制器(Contro…...

如何利用AI提高内容生产效率?
如何利用AI提高内容生产效率? 简介:探讨如何通过AI技术提升内容生产的效率和质量。 方向一:自动化内容生成 自动化内容生成是一种利用人工智能技术来自动创建文本、图像、音频等内容的方法。 以下是一些常见的自动化内容生成方式: 基于…...

C++ stack、queue以及deque
1、stack和queue常用接口 严格来说栈和队列的实现是容器适配器 1、常用接口: 栈:top、push、pop、size、emptystack - C Reference (cplusplus.com) 队列:top、push、pop、swap、size、emptyqueue - C Reference (cplusplus.com) 2、deque&a…...

科沃斯,「扫地茅」荣光恐难再现
作者 | 辰纹 来源 | 洞见新研社 科沃斯恐怕已经很难再回到被市场誉为“扫地茅”时的荣光了。 不久前,科沃斯发布2023年财报,报告期内营业收入155亿,同比仅增长1.16%,归母净利润6.12亿元,同比下降63.96%,直…...

双向BFS算法学习
双向BFS算法学习 推荐练习题 力扣“127”题:单词接龙 “752”题:打开轮盘锁 这里推荐一篇力扣题解 双向BFS 这里使用打开轮盘锁的题干进行举例: 你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: ‘0’, ‘1’, ‘2’,…...
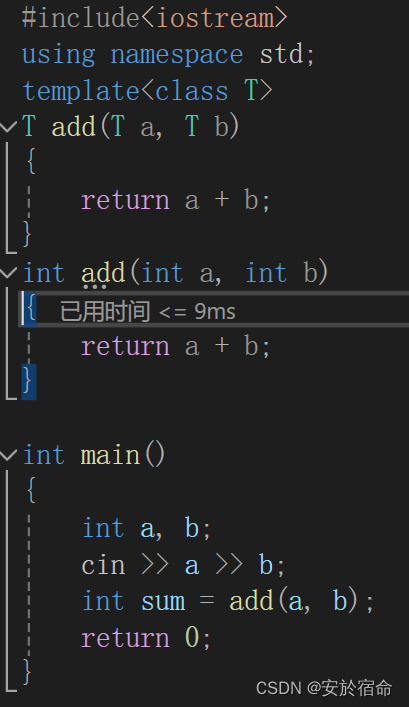
C++从入门到精通---模版
文章目录 泛型编程函数模版模版参数的匹配原则类模版类模版的定义格式类模版的实例化 总结 泛型编程 泛型编程是一种编程范式,旨在实现通用性和灵活性。它允许在编写代码时使用参数化类型,而不是具体的类型,从而使代码更加灵活和可重用。 在…...
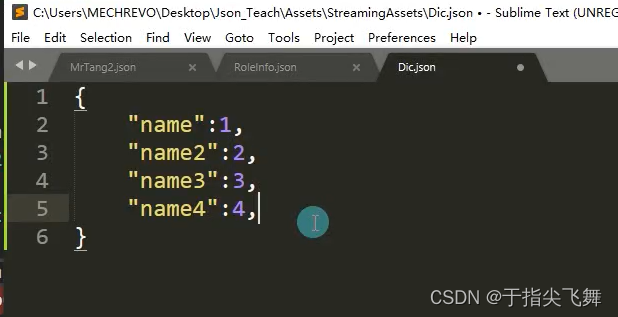
Unity数据持久化之Json
Json概述 Json是什么? 全称:JavaScript对象简谱(JavaScript Object Notation) Json是国际通用的一种轻量级的数据交换格式 主要在网络通讯中用于传输数据,或本地数据存储和读取 易于人阅读和编写,同时也易于机器解析和生成,并有效地提升网络传输效率 我们一般使用Json文件来…...

LeetCode 35.搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 示例 1: 输入: nums [1,3,5,6], target 5 输出: 2 示例 2: 输入…...
速来get!多微信聚合聊天功能大揭秘!
随着网络时代的发展,微信成为了职场中不可或缺的沟通工具,很多人都有着多个微信号,而要想高效管理这些账号,那就少不了工具的帮忙。 通过微信管理系统,可以轻松实现多个微信号聚合聊天,提高沟通效率。 1、…...
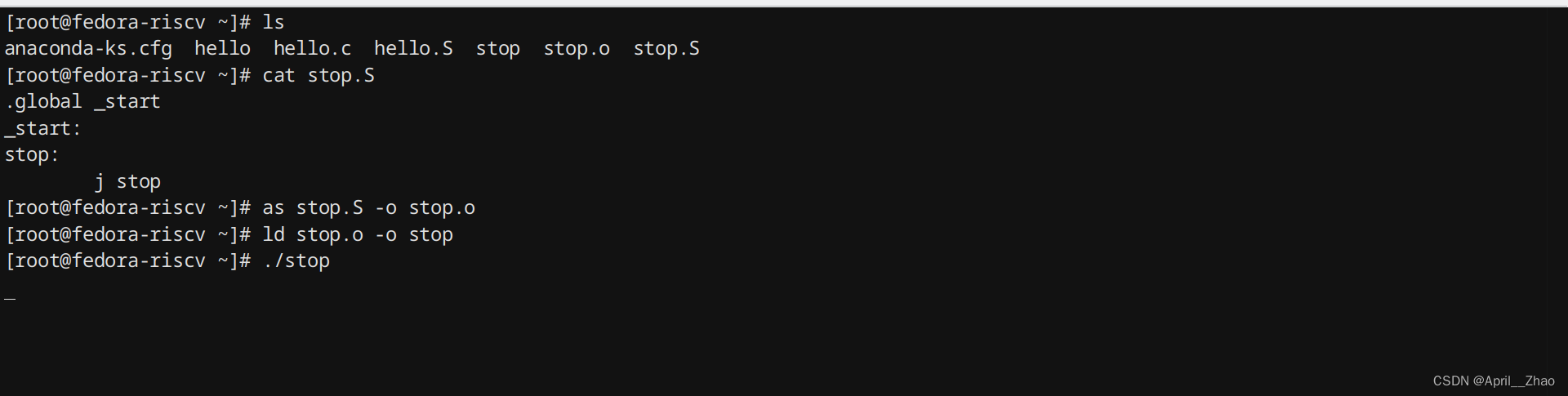
【跟我学RISC-V】(一)认识RISC-V指令集并搭建实验环境
目录 写在前面 一、RISC-V指令集简介 1、什么是ISA 2、有哪些ISA 3、CISC和RISC 4、什么是RISC-V 1. RISC 的起源 2. RISC-I 和 RISC-II 3. RISC 发展和商业化 4. RISC-V 的诞生 5、RISC-V生态的特点 6、RISC-V指令集的特点 1. 开源 2. 社区化 3. 设计简洁 4. 模…...

如何使用google.protobuf.Struct?
google.golang.org/protobuf/types/known/structpb 包提供了一种方式来创建和操作 google.protobuf.Struct 类型的数据。google.protobuf.Struct 是一种灵活的数据类型,可以表示任何结构化数据。 以下是如何使用 structpb 包的一些示例: 创建 Struct&a…...

Vue3 + TS + Element-Plus 封装的 Dialog 弹窗组件
弹窗组件中自定义了header 增加了全屏,svg-icon 没有的话可能会报错,换成自己的图标就可以 <template><el-dialog:dialogHeight"dialogHeight":title"dialogTitle"class"dialog min-w-70"v-model"dialogVi…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...

Linux入门(十五)安装java安装tomcat安装dotnet安装mysql
安装java yum install java-17-openjdk-devel查找安装地址 update-alternatives --config java设置环境变量 vi /etc/profile #在文档后面追加 JAVA_HOME"通过查找安装地址命令显示的路径" #注意一定要加$PATH不然路径就只剩下新加的路径了,系统很多命…...

Android Framework预装traceroute执行文件到system/bin下
文章目录 Android SDK中寻找traceroute代码内置traceroute到SDK中traceroute参数说明-I 参数(使用 ICMP Echo 请求)-T 参数(使用 TCP SYN 包) 相关文章 Android SDK中寻找traceroute代码 设备使用的是Android 11,在/s…...

若依项目部署--传统架构--未完待续
若依项目介绍 项目源码获取 #Git工具下载 dnf -y install git #若依项目获取 git clone https://gitee.com/y_project/RuoYi-Vue.git项目背景 随着企业信息化需求的增加,传统开发模式存在效率低,重复劳动多等问题。若依项目通过整合主流技术框架&…...
