卷积神经网络(CNN)
大家好,这里是七七,今天来更新关于CNN相关的内容同了。本文是针对CNN原理的说明,但对于小白不是非常友好,建议先掌握神经网络相应知识再进行阅读哦。
一、卷积与互相关
卷积
卷积运算是对两个函数进行的一种数学运算,结果是一个新的函数,如果第一个函数为f(x),第二个为g(x),那么其卷积运算被定义为
对于这种运算,如果用手算的话,我们一般先画出f(t),再画出g(t),然后再对g(t)沿y轴翻过去变为g(-t),然后根据偏移量x来进行平移,最后再相乘,就可以得到对应点的卷积值了
值得一提的是,卷积运算满足交换律
互相关
互相关运算与卷积运算极为相似,其公式是这样的
计算过程同上,不再赘述。
值得一提的是,互相关运算不满足交换律
二、卷积核与特征映射图
在图像处理领域中,我们经常使用卷积神经网络(CNN)来进行处理。一般来说,用卷积操作或互相关操作,两者的作用是完全相同的。但出于算法简便性考虑,一般用互相关运算。其实很多神经网络平台提供的库函数中所使用的就是互相关而非卷积,但习惯地称之为卷积。
再用CNN处理图像时,待处理的图像称之为输入,并表示为一个二元离散函数f(m,n)。为了从图片中提取出来特征,我们还需要另一个函数与图像进行卷积,从而提取出相应的特征,而对应的函数就是卷积核,或核函数g(n,m)。卷积的结果是一个新的二元离散函数,被称为特征映射图。这一过程被称为特征提取。
三、CNN的一般结构
- 在第二部介绍过特征提取物过程,就是用核函数与原始数据进行卷积,从而提取出特征。
- 下一步就是用激活函数对特征映射图进行非线性处理,如把小于0的数据都变为0。
- 接着就是采用池化函数分别对特征图进行池化,原理就是使用图像中某个位置及其周边相邻位置的总体统计特征来代替该位置的取值。可以采用最大池化、平均池化等一系列方法。池化的目的是亚索图像的尺寸,凸显特征。
- 最后呢,就是需要将池化后的数据展开为1维的数据,然后投入MLP中进行训练。
在这一过程中,也有一些术语,这里简要介绍一下
- 卷积级:将原始图像与核函数进行卷积这一过程
- 探测级:用激活函数对特征映射图进行非线性处理
- 池化级:池化这一过程
- 卷积层:卷积级、探测级、池化级合起来
因此呢,框架也就基本确定了,CNN的一般架构在大的层面上可分为卷积层+MLP层。其中卷积层权值不变,MLP层权值会改变。
当然,也可以设立很多个卷积层1、卷积层2......;卷积层中也可能存在某些带训练的参数(如偏移量)。
三、边界策略和池化
边界策略
一般来说,输入图像的尺寸远大于核函数的尺寸,而特征图的尺寸不仅取决于原始尺寸和核函数,与边界策略也有关系。
所幸的是,边界策略一般不是那么重要,因为一般来说,图像的特征更多会集中在中心,与边界关系不大
池化
这里比较重要的是步幅,就是每次池化窗口移动的距离。最为常见的情况是等于池化窗口边长-1。
池化还有一个很重要的特征,就是对局部微小位移的不变性。也就是说,被池化的图像中所有像素或部分像素发生了微小位移后,池化的结果并不会发生改变。
相关文章:
卷积神经网络(CNN)
大家好,这里是七七,今天来更新关于CNN相关的内容同了。本文是针对CNN原理的说明,但对于小白不是非常友好,建议先掌握神经网络相应知识再进行阅读哦。 一、卷积与互相关 卷积 卷积运算是对两个函数进行的一种数学运算,…...

Linux入门攻坚——22、通信安全基础知识及openssl、CA证书
Linux系统常用的加解密工具:OpenSSL,gpg(是pgp的实现) 加密算法和协议: 对称加密:加解密使用同一个秘钥; DES:Data Encryption Standard,数据加密标准&…...

无障碍Web开发:遵循WCAG标准构建包容性用户体验
无障碍Web开发旨在确保所有用户,无论其身体条件或能力如何,都能轻松、有效地访问和使用Web内容。遵循Web Content Accessibility Guidelines (WCAG) 标准是实现这一目标的关键。以下是一些基于WCAG标准的无障碍Web开发实践,以构建更具包容性的…...
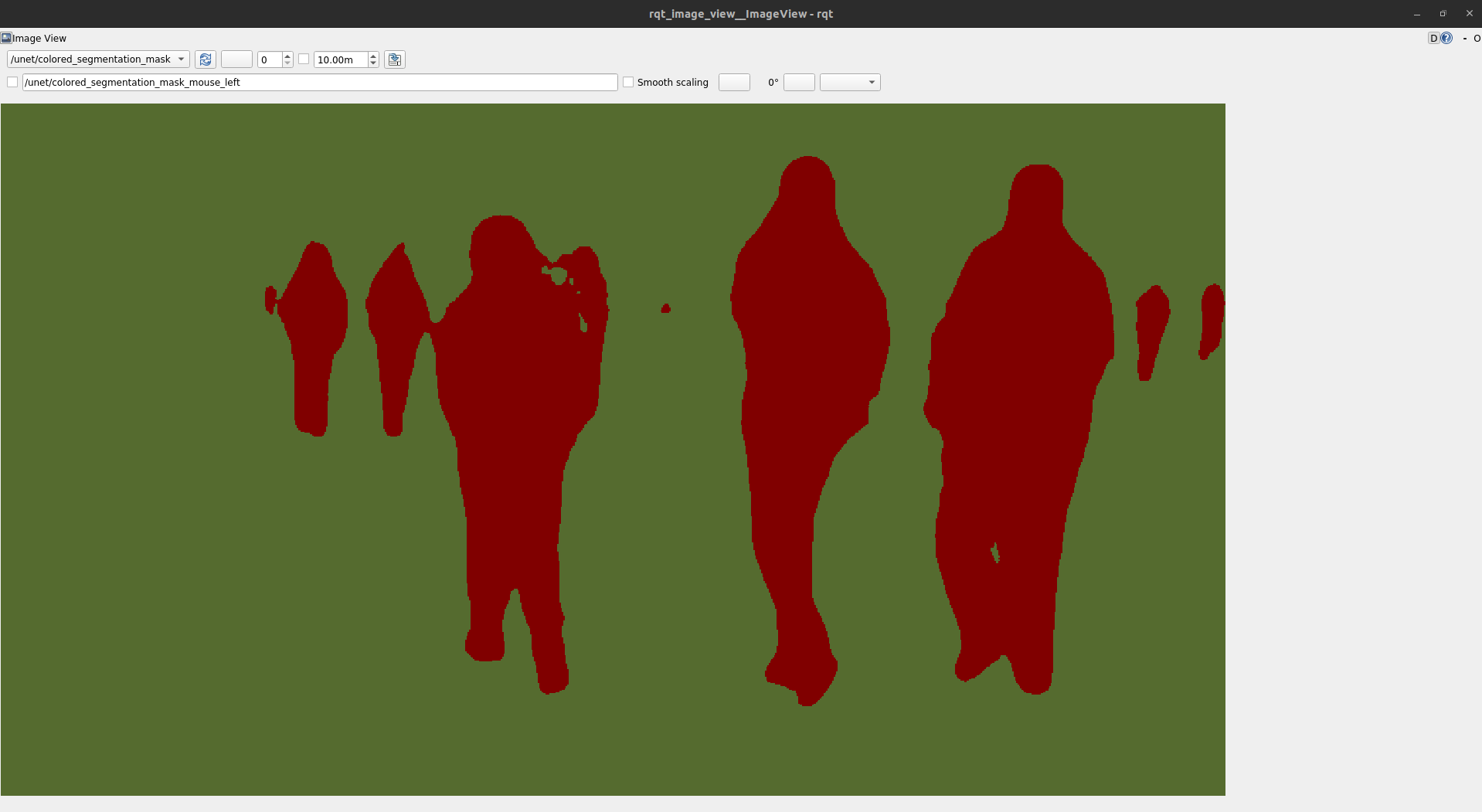
Isaac Sim 3(学习笔记5.8)
Isaac Sim 利用深度学习获取mask掩码图 参考内容 Kubernetes官网 在 Linux 系统中安装并设置 kubectl | Kubernetes准备开始 kubectl 版本和集群版本之间的差异必须在一个小版本号内。 例如:v1.30 版本的客户端能与 v1.29、 v1.30 和 v1.31 版本的控制面通信。 用…...

对象定义成final类型还能改变吗
如果一个Java对象被定义为final类型,那么它的引用不能被改变,但是对象本身的状态仍然可以被修改。这意味着你可以改变final对象的属性,但是不能将其引用指向另一个对象。 例如,下面的代码中,虽然person对象被声明为fi…...

Vue Router 路由hash和history模式
文章目录 hash和history模式区别Hash 模式History 模式 在 Vue 中,路由的两种主要模式是 hash 和 history,默认的路由模式是hash模式。。这两种模式决定了 URL 的外观以及浏览器如何处理 URL 的变化。 hash和history模式区别 特性Hash 模式History 模…...

【xrframe】优化ar相机中加载模型效果
方法一:定义渲染width和height //组件生命周期:在视图层布局完成后执行ready() {const info wx.getSystemInfoSync();//在小程序中同步获取系统信息const width info.windowWidth;//获取屏幕的宽度(单位为物理像素)const heigh…...
解决 SyntaxError: Unexpected token ‘.‘ 报错问题
这个报错一般是编译问题,浏览器的版本过低没通过代码 解决办法: 在package.json文件中加上这个 "browserslist": ["> 1%","last 2 versions","not dead","not ie < 6","Android > 4&…...

谷歌插件V3知识点
1.background.js与content.js与popup.js对比: background.js 生命周期:一开始就执行,最早执行且一直执行; 作用:放置全局的、需要一直运行的代码,权限非常高几乎调用所有Chrome api,还可以发起跨域请求; content.js 生…...
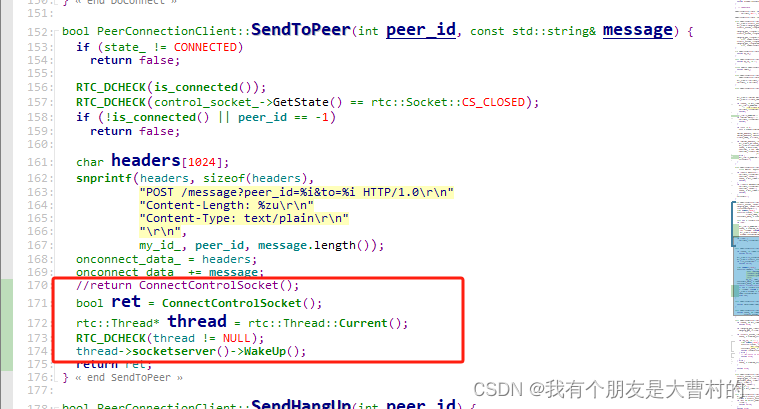
webrtc windows 编译,以及peerconnection_client
webrtc windows环境编译,主要参考webrtc官方文档,自备梯子 depot tools 安装 Install depot_tools 因为我用的是windows,这里下载bundle 的安装包,然后直接解压,最后设置到环境变量PATH。 执行gn等命令不报错&…...

geotrust企业通配符证书2990
随着时代的变化,人们获取信息的方式由报纸、书籍变为手机、电脑,因此很多企事业单位用户开始在互联网中创建网站来进行宣传,吸引客户。为了维护网站安全环境,保护客户数据,企事业单位也开始使用SSL数字证书,…...

网络安全科普:保护你的数字生活
# 网络安全科普:保护你的数字生活 ## 引言 在数字化时代,网络安全已成为每个人都必须面对的问题。从个人隐私保护到金融交易安全,网络的安全性直接关系到我们的日常生活。因此,普及网络安全知识,提高公众的网络安全意…...

Java实战:递归查找指定后缀名的文件
在日常的软件开发中,经常需要处理文件操作。假设我们有一个需求:从一个包含大量JSON文件的文件夹中提取出所有的JSON文件以进行进一步处理。本文将介绍如何利用Java编写一个高效的方法来递归查找指定后缀名的文件。 代码实现: import java.i…...
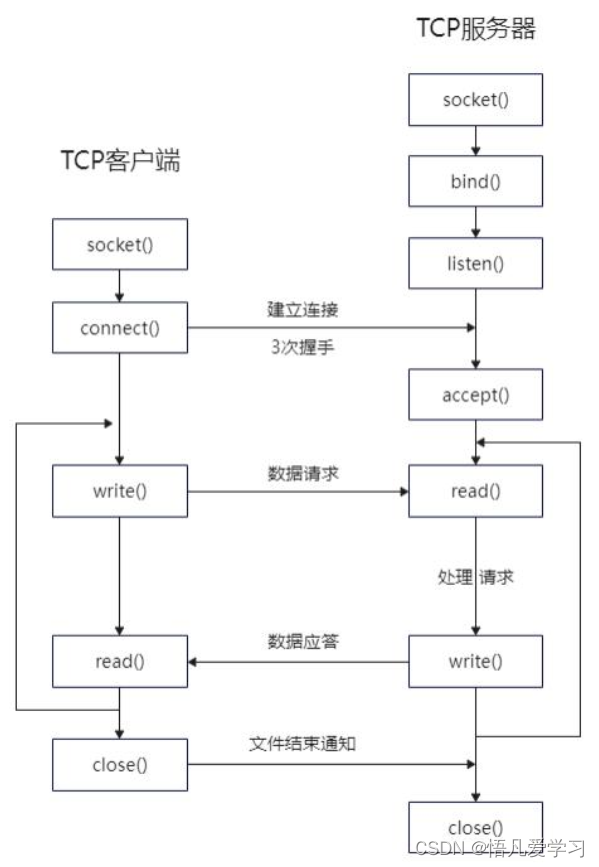
Linux 操作系统网络编程1
目录 1、网络编程 1.1 OSI 网络七层模型 1.1.1 OSI 参考模型 1.1.2 网络数据传输过程 2 传输层通信协议 2.1 TCP 2.1.1 TCP的3次握手过程 2.1.2 TCP四次挥手过程 2.2 UDP 3 网络编程的IP地址 4 端口 5 套接字 1、网络编程 1.1 OSI 网络七层模型 1.1.1 OSI 参考模型…...
成员、shared_future)
future wait_for()成员、shared_future
future wait_for()成员 wait_for():等待其异步操作操作完成或者超出等待,用于检查异步操作的状态。wait_for()可以接受一个std::chrono::duration类型的参数,它表示等待的最大时间,会返回一个std::future_status枚举值࿰…...

C++ list介绍(迭代器失效)
一、常用接口 reverse逆置 sort排序(默认升序) 仿函数greater<int> merge合并,可以全部合并,也可以一部分合并 unique:去重(先排序,再去重) remove:删除e值&#…...

codeforces 1809C
很巧妙的构造 题目链接 题目大意 要求构造长度为 n n n的数组满足以下条件 任意 i i i, − 1000 < a [ i ] < 1000 -1000<a[i]<1000 −1000<a[i]<1000有 k k k个和为正数的子串其余子串和为负数 思路 我们发现与子数组内元素的和有关&…...
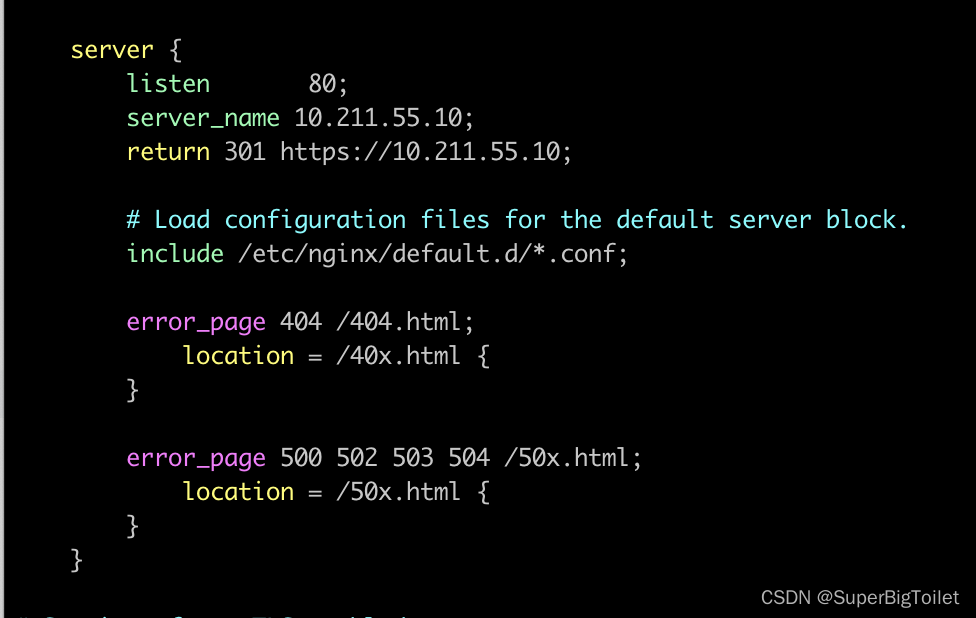
Nginx part3 创建一个https的网站
目录 HTTPS 公钥和密钥 加密解密方式: https搭建步骤 强调一下 1、准备环境 2、配置文件 3、制作证书 4、进行设置 HTTPS 啥是https,根据百度:HTTPS (全称:Hypertext Transfer Protocol Secure)&a…...

事件高级。
一、注册事件(绑定事件) 就是给元素添加事件 注册事件有两种方式:传统方式和方法监听注册方式 1 传统注册方式 方法监听注册事件 2、 addEventListener 事件监听方式 里面的事件类型是字符串,必定加引号,而且不带o…...

Vue从入门到实战Day04
一、组件的三大组成部分(结构/样式/逻辑) 1. scoped样式冲突 默认情况:写在组件中的样式会全局生效 -> 因此很容易造成多个组件之间的样式冲突问题。 1. 全局样式:默认组件中的样式会作用到全局 2. 局部样式:可以…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...
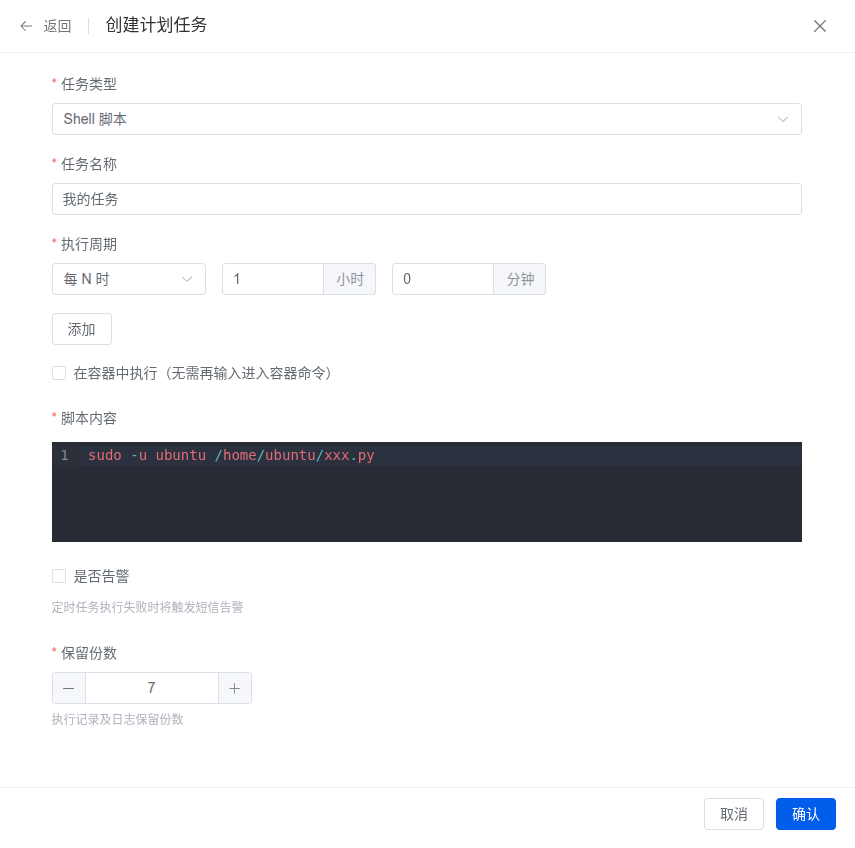
【Linux】使用1Panel 面板让服务器定时自动执行任务
服务器就是一台24小时开机的主机,相比自己家中不定时开关机的主机更适合完成定时任务,例如下载资源、备份上传,或者登录某个网站执行一些操作,只需要编写 脚本,然后让服务器定时来执行这个脚本就可以。 有很多方法实现…...

联邦学习带宽资源分配
带宽资源分配是指在网络中如何合理分配有限的带宽资源,以满足各个通信任务和用户的需求,尤其是在多用户共享带宽的情况下,如何确保各个设备或用户的通信需求得到高效且公平的满足。带宽是网络中的一个重要资源,通常指的是单位时间…...
