简要介绍三大脚本语言 Shell、Python 和 Lua
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/

脚本语言是一种用于自动化操作系统任务和应用程序功能的编程语言。它们通常用于编写小到中等规模的程序,以提高任务执行的速度和效率。在众多脚本语言中,Shell、Python 和 Lua 是最为常见和广泛应用的。
Shell 脚本是运行在 Unix 或 Linux Shell 中的脚本程序。Shell 是一个特殊的用户程序,提供了用户使用操作系统服务的接口。Shell 脚本允许用户编写一系列命令,这些命令将会被 Shell 顺序执行。通过 Shell 脚本,可以自动化日常的任务,如文件管理、程序执行和文本处理等。
Python 是一种高级、解释型的编程语言,以其清晰的语法和强大的标准库而著名。Python 广泛应用于 Web 开发、数据分析、人工智能等众多领域。Python 的简洁语法和动态类型,使其成为初学者和专业开发者都非常喜欢的脚本语言。Python 还支持面向对象、命令式、函数式和过程式编程范式,提供了极大的灵活性和表达力。
Lua 是一个轻量级、高级、多范式的编程语言,主要用于应用程序中的嵌入式使用。Lua 设计目的是为了提供一种灵活的编程方法,用于配置软件和应用程序,特别是在需要嵌入脚本的游戏和工业应用中。Lua 语言简洁,APIs 简单,易于嵌入其他应用程序中。由于其性能出色,Lua 被广泛应用于游戏开发、Web 服务器脚本和图形用户界面编程等领域
这三种脚本语言各具特色和优势。Shell 脚本擅长直接控制操作系统和执行批处理任务;Python 则因其通用性和丰富的库支持,在数据科学和 Web 开发领域占据主导地位;而 Lua 则因其轻量级和高性能,在嵌入式系统和游戏开发中受到广泛应用。选择那种脚本语言应基于具体任务需求和个人偏好。
相关文章:

简要介绍三大脚本语言 Shell、Python 和 Lua
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 脚本语言是一种用于自动化操作系统任务和应用程序功能的编程语言。它们通常用于编写小到中等规模的程序,以提高任务执行的速度和效率。在众多脚本语言中,Shell、Python 和 Lua 是…...
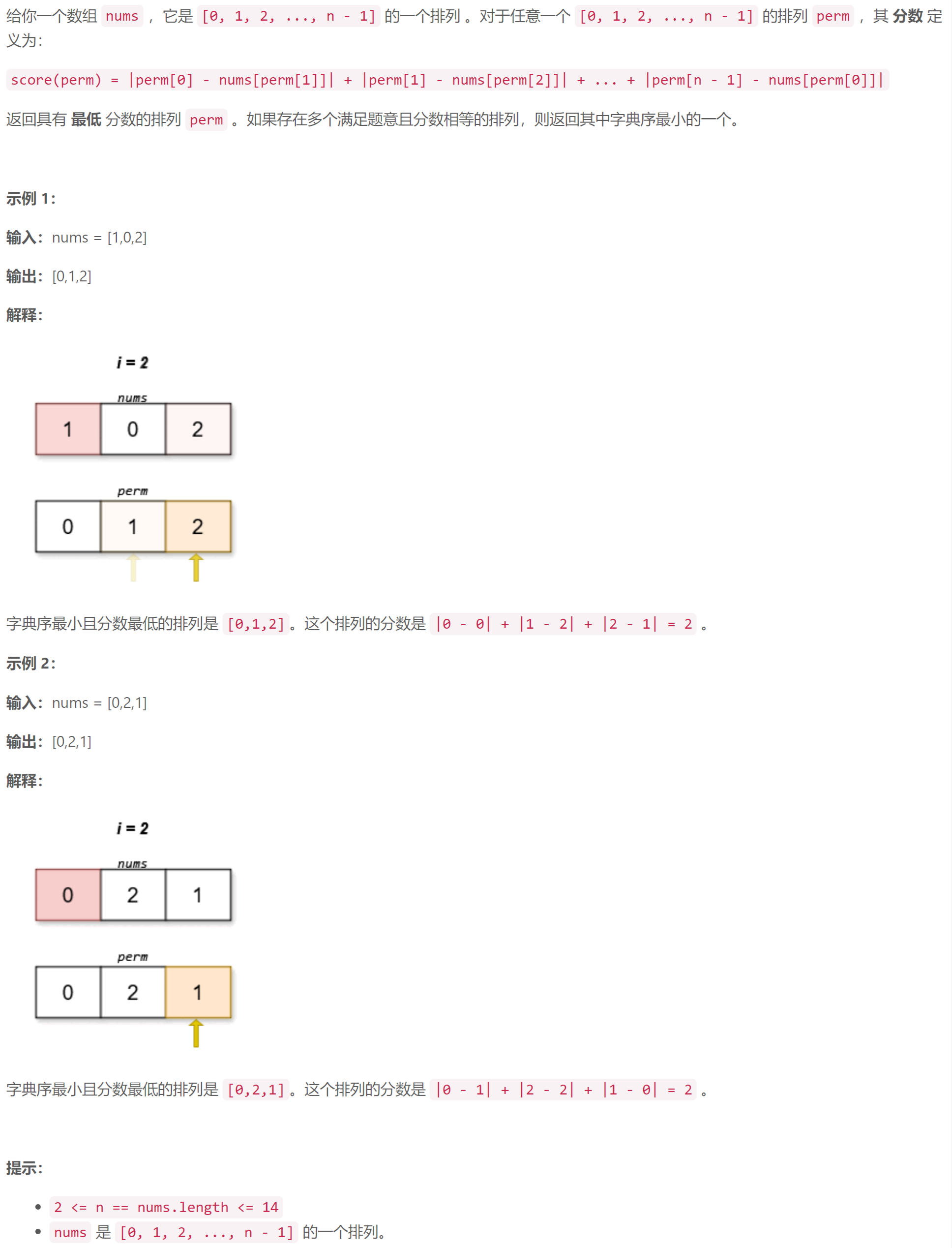
第 397 场 LeetCode 周赛题解
A 两个字符串的排列差 模拟:遍历 s s s 记录各字符出现的位置,然后遍历 t t t 计算排列差 class Solution {public:int findPermutationDifference(string s, string t) {int n s.size();vector<int> loc(26);for (int i 0; i < n; i)loc[s…...
文件存储解决方案-阿里云OSS
文章目录 1.菜单分级显示问题1.问题引出1.苹果灯,放到节能灯下面也就是id大于1272.查看菜单,并没有出现苹果灯3.放到灯具下面id42,就可以显示 2.问题分析和解决1.判断可能出现问题的位置2.找到递归返回树形菜单数据的位置3.这里出现问题的原因…...
基于Java的飞机大战游戏的设计与实现(论文 + 源码)
关于基于Java的飞机大战游戏.zip资源-CSDN文库https://download.csdn.net/download/JW_559/89313362 基于Java的飞机大战游戏的设计与实现 摘 要 现如今,随着智能手机的兴起与普及,加上4G(the 4th Generation mobile communication &#x…...
Vue路由开启步骤
1.在控制台输入命令 //控制台下载安装npm add vue-router3.6.5 2.在main.js下导入并注册组件 import Vue from vue import App from ./App.vue//控制台下载安装npm add vue-router3.6.5 //导入 import VueRouter from "vue-router";//注册 Vue.use(VueRouter) con…...

【碎片知识】2024_05_15
char int long float double运算的时候是从低转到高的,表达式的类型会自动提升或者转 换为参与表达式求值的最上级类型. 关于代码的说法正确的是( ) #include <stdio.h> int main() {int x -1;unsigned int y 2;if (x > y){printf…...
彩虹聚合DNS管理系统
聚合DNS管理系统可以实现在一个网站内管理多个平台的域名解析,目前已支持的域名平台有:阿里云、腾讯云、华为云、西部数码、CloudFlare。本系统支持多用户,每个用户可分配不同的域名解析权限;支持API接口,支持获取域名…...
服务网格 SolarMesh v1.13 重磅发布
SolarMesh是行云创新推出的流量治理平台,它基于Istio,为部署在K8s集群上的应用提供全面的流量治理能力。 在之前的版本中,SolarMesh提供的能力有:流量视图,流量控制策略批量配置,API级别的流量数据采集和展…...
三大平台直播视频下载保存方法
终于解决了视频号下载的问题,2024年5月15日亲测可用。 而且免费。 教程第二部分,有本地电脑无法下载的解决方案。 第一部分:使用教程(正常) 第1步:下载安装包 下载迅雷网盘搜索:大海福利合集…...
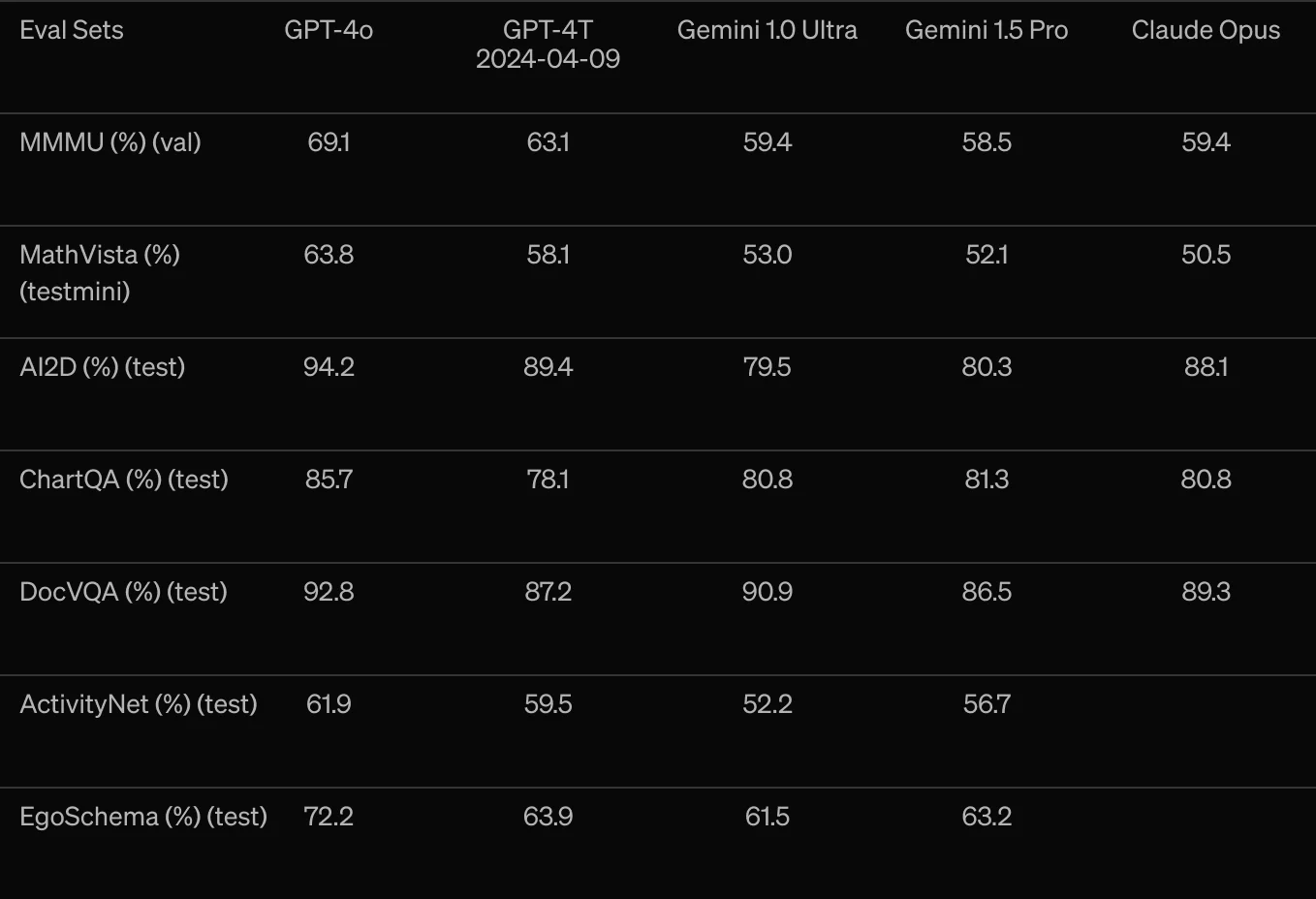
OpenAI GPT-4o - 介绍
本文翻译整理自: Hello GPT-4o https://openai.com/index/hello-gpt-4o/ 文章目录 一、关于 GPT-4o二、模型能力三、能力探索四、模型评估1、文本评价2、音频 ASR 性能3、音频翻译性能4、M3Exam 零样本结果5、视觉理解评估6、语言 tokenization 六、模型安全性和局限…...

QTreeView学习 branch 虚线设置
1、方法一: #include <QStyleFactory> ui.treeView->setStyle(QStyleFactory::create("windows")); 2、方法二: QString strtyle2 R"( QTreeView::branch:has-siblings:!adjoins-item { border-image: url(:/TreeViewDe…...
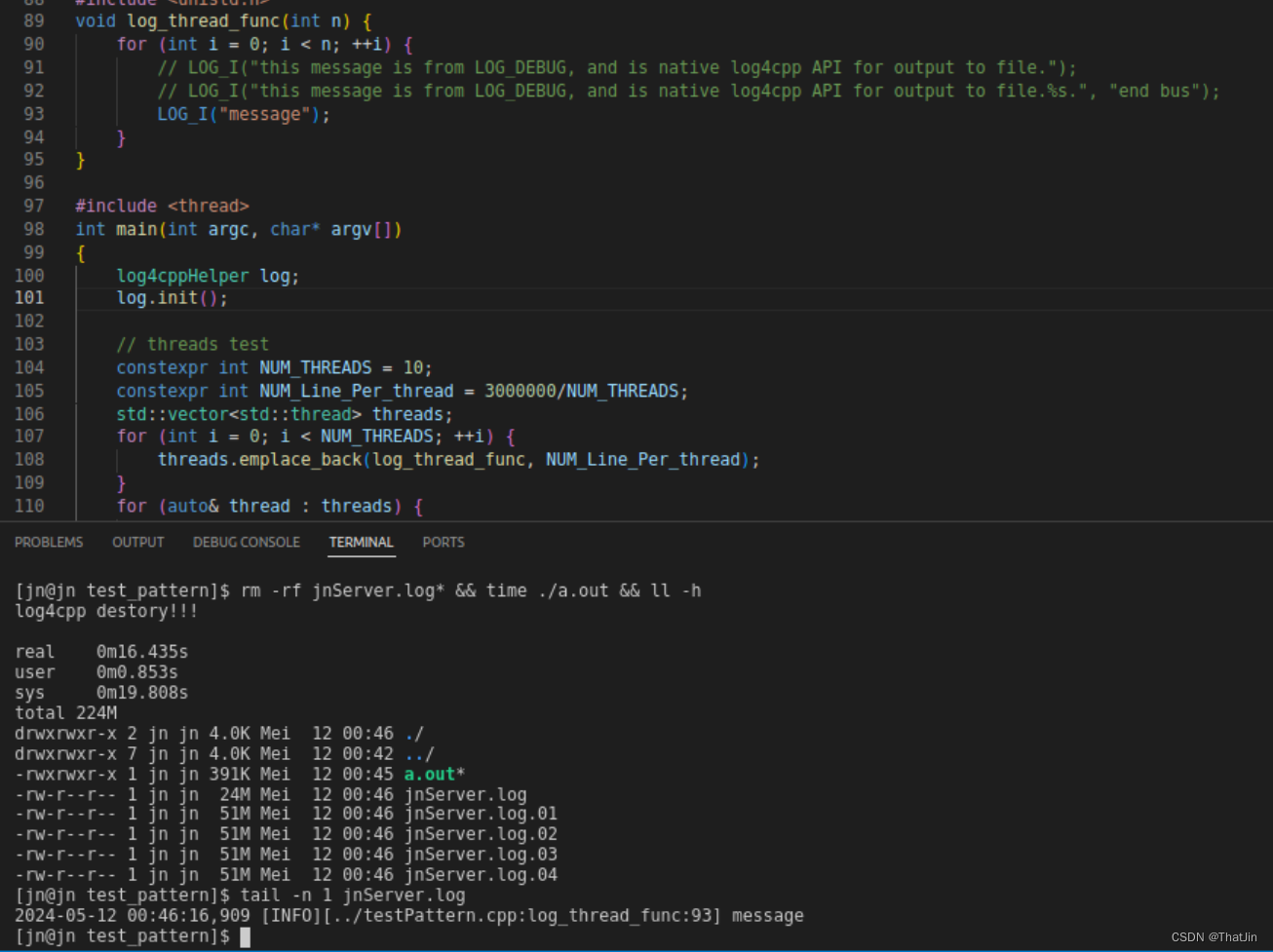
C++ 日志库 log4cpp 编译、压测及其范例代码 [全流程手工实践]
文章目录 一、 log4cpp官网二、下载三、编译1.目录结构如下2.configure 编译3.cmake 编译 四、测试五、压测源码及结果1.运行环境信息2.压测源码3.压测结果 文章内容:包含了对其linux上的完整使用流程,下载、编译、安装、测试用例尝试、以及一份自己写好…...
)
python数据处理与分析入门-pandas使用(4)
往期文章: pandas使用1pandas使用2pandas使用3 pandas使用技巧 创建一个DF对象 # 首先创建一个时间序列 dates pd.date_range(20180101, periods6) print(dates)# 创建DataFrame对象,指定index和columns标签 df pd.DataFrame(np.random.randn(6,4), …...
)
操作系统-单片机进程状态问题(三态模型问题)
例题:在单处理机计算机系统中有1台打印机、1台扫描仪,系统采用先来先服务调度算法。假设系统中有进程P1、P2、P3、P4,其中P1为运行状态,P2为就绪状态,P3等待打印机,P4等待扫描仪。此时,若P1释放…...
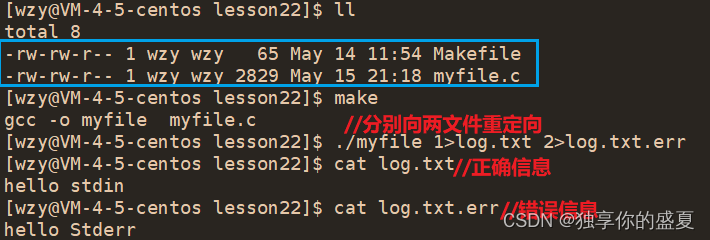
Linux文件:重定向底层实现原理(输入重定向、输出重定向、追加重定向)
Linux文件:重定向底层实现原理(输入重定向、输出重定向、追加重定向) 前言一、文件描述符fd的分配规则二、输出重定向(>)三、输出重定向底层实现原理四、追加重定向(>>)五、输入重定向…...
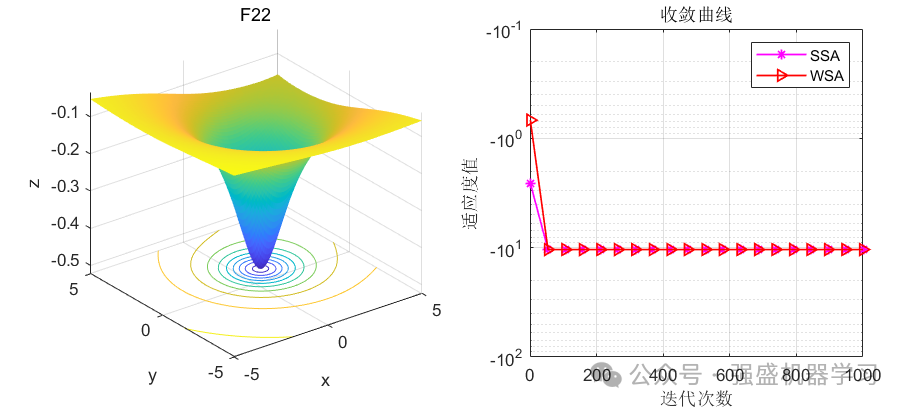
波搜索算法(WSA)-2024年SCI新算法-公式原理详解与性能测评 Matlab代码免费获取
声明:文章是从本人公众号中复制而来,因此,想最新最快了解各类智能优化算法及其改进的朋友,可关注我的公众号:强盛机器学习,不定期会有很多免费代码分享~ 目录 原理简介 一、初始化阶段 二、全…...
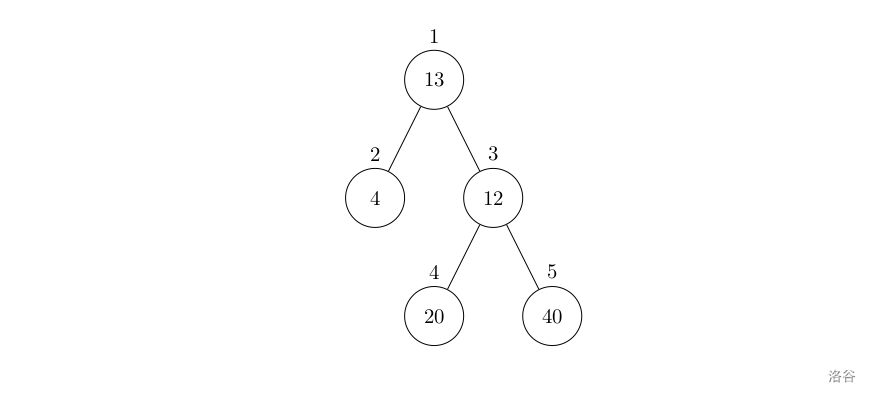
洛谷P1364 医院设置
P1364 医院设置 题目描述 设有一棵二叉树,如图: 其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,…...

哈希表的理解和实现
目录 1. 哈希的概念 (是什么) 2. 实现哈希的两种方式 (哈希函数) 2.1. 直接定址法 2.2. 除留余数法 2.2.1. 哈希冲突 3. 补充知识 3.1. 负载因子 3.2. 线性探测和二次探测 4. 闭散列实现哈希表 (开放定址法) 4.1. 开放定址法的实现框架 4.2. Xq::hash_table::insert…...
)
分治算法(Divide-and-Conquer Algorithm)
分治算法(Divide-and-Conquer Algorithm)是一种重要的计算机科学和数学领域的通用问题解决策略。其基本思想是将一个复杂的大规模问题分割成若干个规模较小、结构与原问题相似但相对简单的子问题来处理。这些子问题相互独立,分别求解后再通过…...
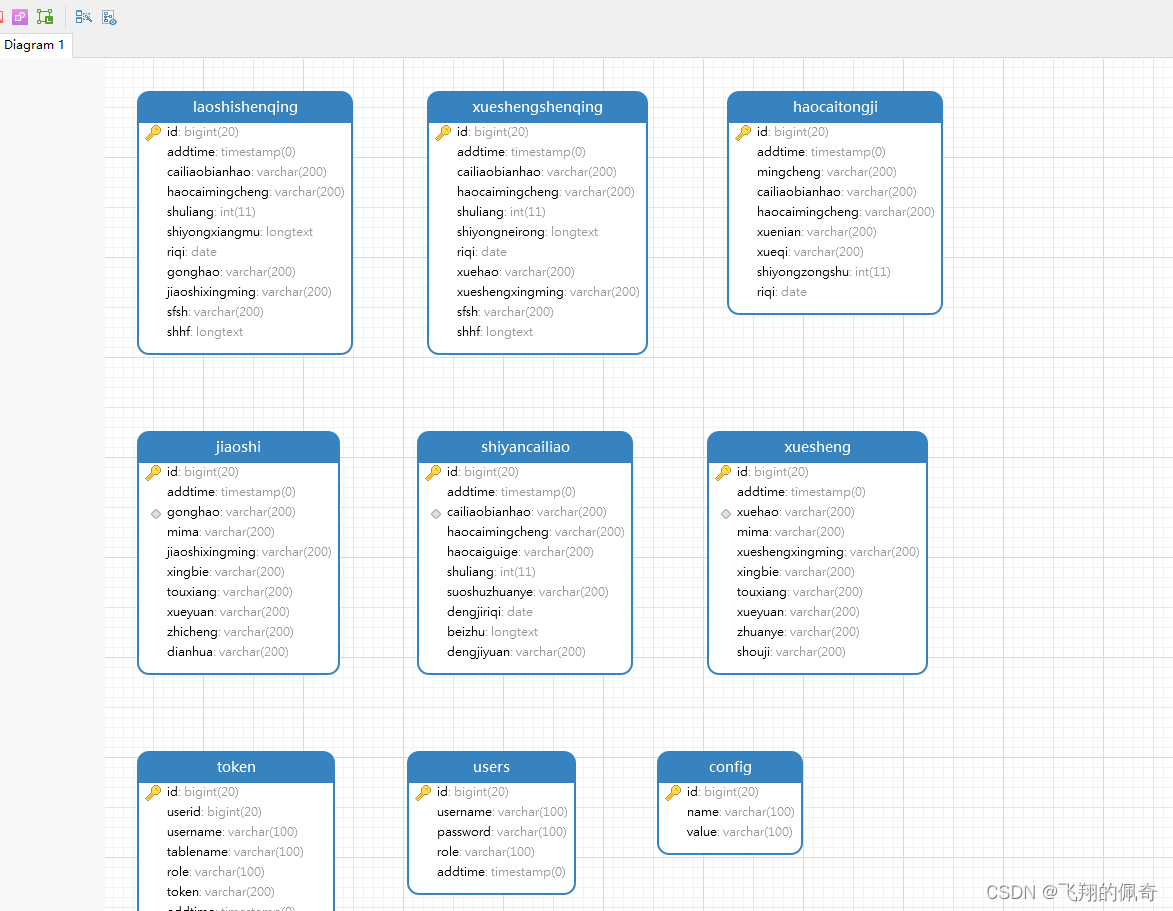
Java项目:基于ssm框架实现的实验室耗材管理系统(B/S架构+源码+数据库+毕业论文+答辩PPT)
一、项目简介 本项目是一套基于ssm框架实现的实验室耗材管理系统 包含:项目源码、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过严格调试,eclipse或者idea 确保可以运行! 二、技术实现 jdk版本:1.8 …...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...
