线性三角化
点的线性三角化
- 输入一堆的点
[ R w c , t w c , p u c ] [R_{wc},t_{wc},p_{uc}] [Rwc,twc,puc] - 转化成空间的一系列射线
[ P w i , t w i ] , P w i = t w c , t w i = R w c × p u c [P_{wi},t_{wi}],P_{wi}=t_{wc},t_{wi}=R_{wc}\times p_{uc} [Pwi,twi],Pwi=twc,twi=Rwc×puc - 点和射线之间的关系是
P = P i + d i × t i P=P_i+d_i\times t_i P=Pi+di×ti - 方程改写为
[ t i ] × P = t i × P i [t_i]^{\times}P=ti\times P_i [ti]×P=ti×Pi - 方程的表达式为
A = [ [ t 1 ] × . . . [ t n ] × ] A= \begin{bmatrix} [t_1]^{\times} \\ ... \\ [t_n]^{\times} \end{bmatrix} A= [t1]×...[tn]×
b = [ t 1 × P 1 . . . t n × P n ] b= \begin{bmatrix} t_1\times P_1 \\ ... \\ t_n\times P_n \end{bmatrix} b= t1×P1...tn×Pn
A x = b Ax = b Ax=b
直线的线性三角化
- 输入一堆检测的线段
[ R c w , t c w , p u c 1 , p u c 2 ] [R_{cw},t_{cw},p_{uc1},p_{uc2}] [Rcw,tcw,puc1,puc2] - 两条检测射线形成的面的法线
n c ⃗ = p u c 1 × p u c 2 \vec{n_c}=p_{uc1}\times p_{uc2} nc=puc1×puc2 - 直线上点的坐标形成的射线和法线是垂直的
n c ⃗ × P c = 0 n c ⃗ × ( R c w P w + t c w ) = 0 [ n c ⃗ ] × R c w P w = − n c ⃗ × t c w \vec{n_c} \times P_c = 0 \\ \vec{n_c}\times(R_{cw}P_w + t_{cw}) = 0 \\ [\vec{n_c}]^{\times}R_{cw}P_w=-\vec{n_c}\times t_{cw} nc×Pc=0nc×(RcwPw+tcw)=0[nc]×RcwPw=−nc×tcw
KaTeX parse error: Expected '}', got '\end' at position 92: …\times}R_{cwn} \̲e̲n̲d̲{bmatrix}
b = [ − n c 1 ⃗ × t c w 1 . . . − n c n ⃗ × t c w n ] b= \begin{bmatrix} -\vec{n_{c1}}\times t_{cw1} \\ ... \\ -\vec{n_{cn}}\times t_{cwn} \end{bmatrix} b= −nc1×tcw1...−ncn×tcwn
A x = b Ax = b Ax=b
相关文章:

线性三角化
点的线性三角化 输入一堆的点 [ R w c , t w c , p u c ] [R_{wc},t_{wc},p_{uc}] [Rwc,twc,puc]转化成空间的一系列射线 [ P w i , t w i ] , P w i t w c , t w i R w c p u c [P_{wi},t_{wi}],P_{wi}t_{wc},t_{wi}R_{wc}\times p_{uc} [Pwi,twi],Pwitwc…...
Golang os.Rename invalid cross-device link的原因
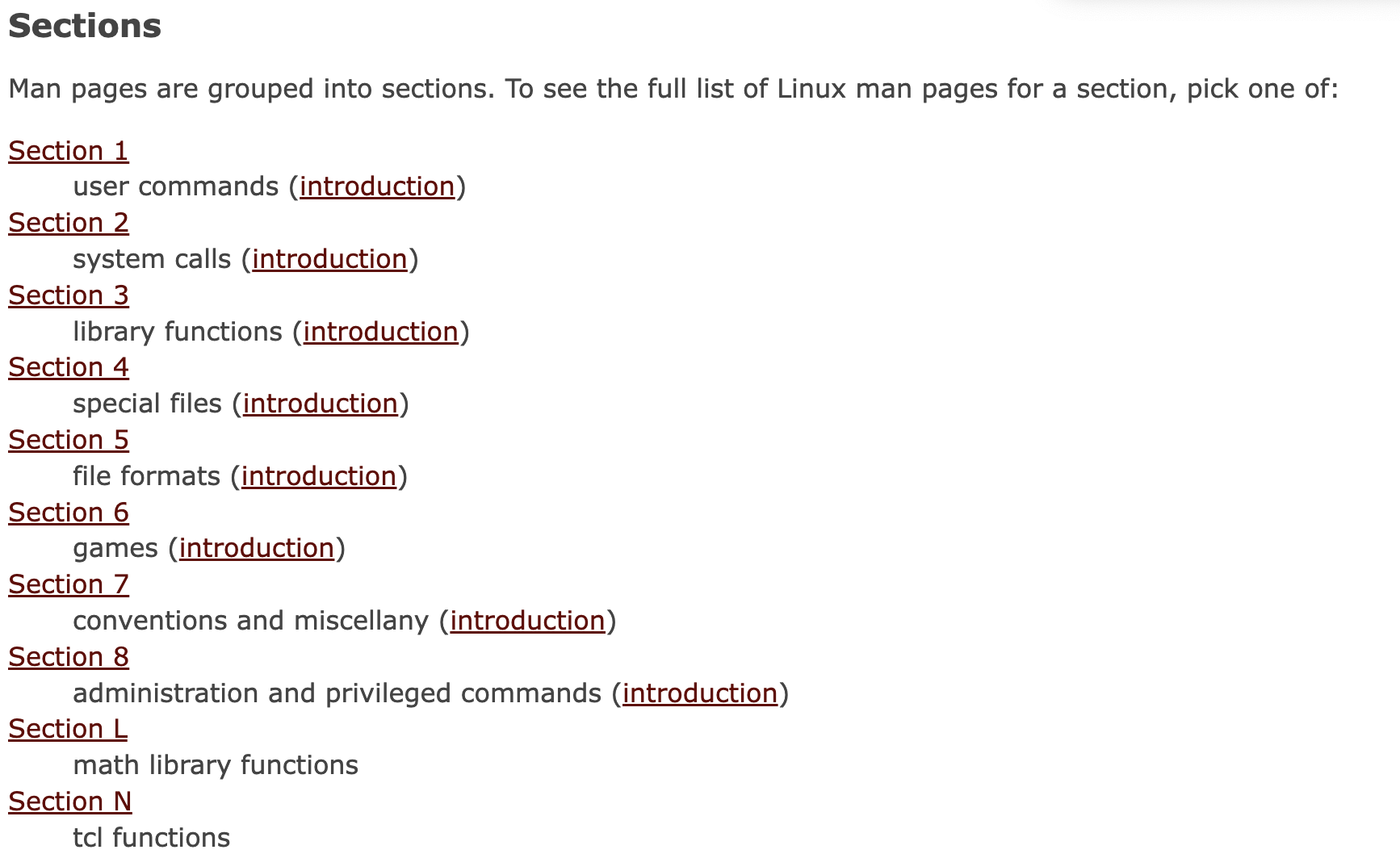
文章目录 背景运行环境 文件系统对比linux下的文件系统mac下的文件系统linux下的mv指令 golang的os.Rename源码os.Renamesyscall.Renamesyscall.RenameatSYS_RENAMEAT是什么 查看系统调用函数文档什么是man pageman page的用法user commandssystem calls renameat不支持跨挂载点…...

Flutter 中的 Badge 小部件:全面指南
Flutter 中的 Badge 小部件:全面指南 在移动应用设计中,徽章(Badge)是一种常见的UI元素,用于吸引用户注意并展示重要信息,如未读消息数量、新通知等。Flutter 通过各种第三方包提供了徽章小部件࿰…...
Java 多线程抢红包
问题需求 一个人在群里发了1个100元的红包,被分成了8个,群里有10个人一起来抢红包,有抢到的金额随机分配。 红包功能需要满足哪些具体规则呢? 1、被分的人数抢到的金额之和要等于红包金额,不能多也不能少。 2、每个人至少抢到1元…...
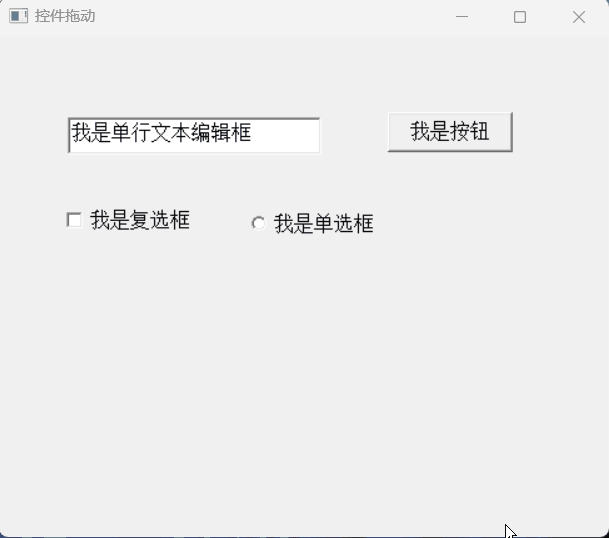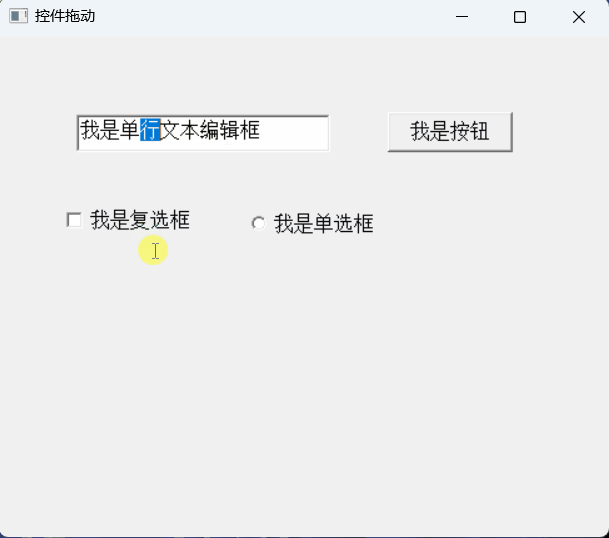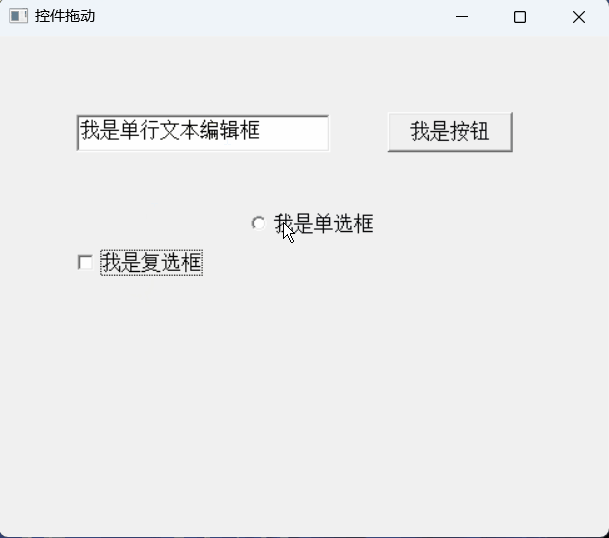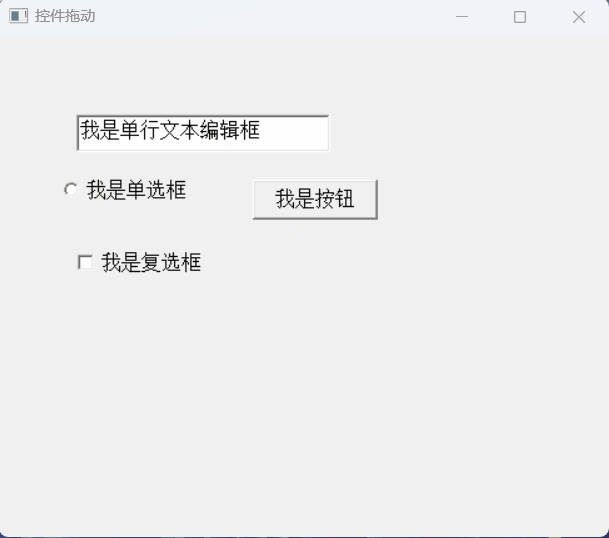
【PB案例学习笔记】-08 控件拖动实现
写在前面 这是PB案例学习笔记系列文章的第8篇,该系列文章适合具有一定PB基础的读者。 通过一个个由浅入深的编程实战案例学习,提高编程技巧,以保证小伙伴们能应付公司的各种开发需求。 文章中设计到的源码,小凡都上传到了gitee…...

读书笔记整理
1.对天才而言,任何努力都如做游戏般容易和有趣,兴趣是发展的原动力。从这个角度来看,通过普通人的劳动是无法创造天才的。 2.让孩子理解语法是很困难的。苦背不如练才是行之有效的办法。孩子们永远是故事迷,在教孩子们外语时&…...

uniapp蓝牙打印图片
前言 这是个蓝牙打印图片的功能,业务是打印界面固定的demo范围,这里通过html2canvas插件生成的图片base64,然后图片base64绘制到canvas中去后,获取canvas中的像素信息,然后对像素信息进行一个灰度值处理,灰…...

Ajax用法总结(包括原生Ajax、Jquery、Axois)
HTTP知识 HTTP(hypertext transport protocol)协议『超文本传输协议』,协议详细规定了浏览器和万维网服务器之间互相通信的规则。 请求报文 请求行: GET、POST /s?ieutf-8...(url的一长串参数) HTTP/1.1 请求头…...

LeetCode 题解:112. 路径总和,递归,JavaScript,详细注释
原题链接: 112. 路径总和 解题思路: 如果求根节点到叶子节点的路径上的节点值之和,假设共有3个节点,那么写成计算式是val1 val2 val3 sum那么将计算式转换就可以得到val3 sum - val1 - val2也就是说,问题可以从…...
Spring Boot的自动配置是如何工作的)
Spring (15)Spring Boot的自动配置是如何工作的
Spring Boot的自动配置是通过条件注解(如ConditionalOnClass,ConditionalOnBean等)和EnableAutoConfiguration注解来实现的。这一机制主要是为了简化配置过程,让开发者在满足特定条件时自动配置Spring应用。接下来,我们…...

【机器学习】—机器学习和NLP预训练模型探索之旅
目录 一.预训练模型的基本概念 1.BERT模型 2 .GPT模型 二、预训练模型的应用 1.文本分类 使用BERT进行文本分类 2. 问答系统 使用BERT进行问答 三、预训练模型的优化 1.模型压缩 1.1 剪枝 权重剪枝 2.模型量化 2.1 定点量化 使用PyTorch进行定点量化 3. 知识蒸馏…...
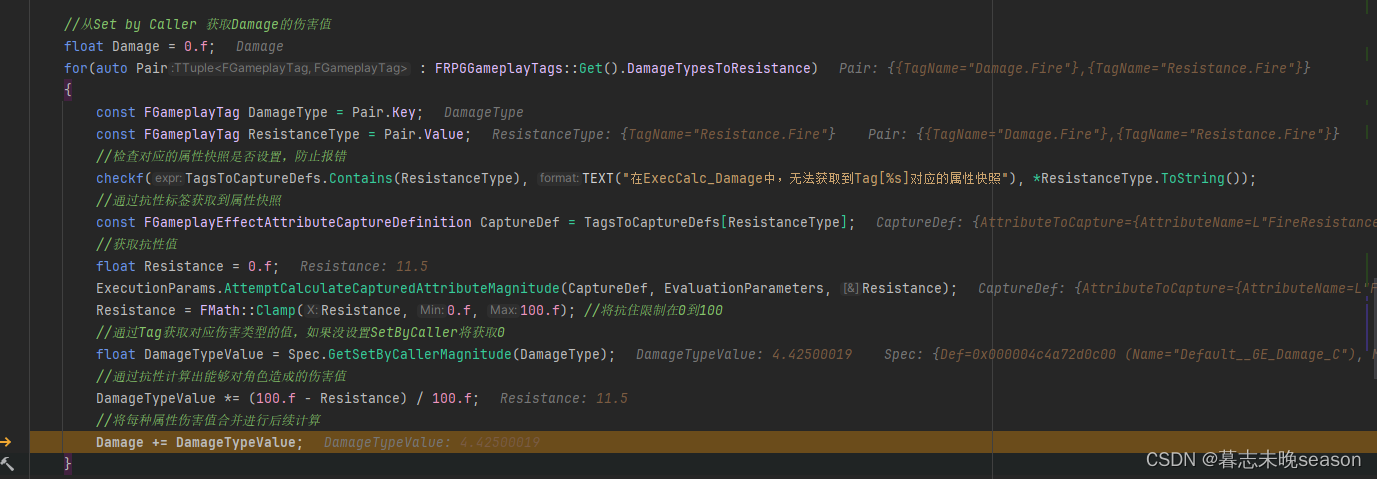
54. UE5 RPG 增加伤害类型
在正常的RPG游戏中,都存在一个类别就是属性伤害,比如,在一个游戏里面有一个火属性的技能,它造成的伤害就是火属性类型的,并且它还有可能有附加伤害,比如给予目标一个灼烧效果,每秒造成多少的火属…...

llama3 微调教程之 llama factory 的 安装部署与模型微调过程,模型量化和gguf转换。
本文记录了从环境部署到微调模型、效果测试的全过程,以及遇到几个常见问题的解决办法,亲测可用(The installed version of bitsandbytes was compiled without GPU support. NotImplementedError: Architecture ‘LlamaForCausalLM’ not sup…...

C++三剑客之std::any(二) : 源码剖析
目录 1.引言 2.std::any的存储分析 3._Any_big_RTTI与_Any_small_RTTI 4.std::any的构造函数 4.1.从std::any构造 4.2.可变参数模板构造函数 4.3.赋值构造与emplace函数 5.reset函数 6._Cast函数 7.make_any模版函数 8.std::any_cast函数 9.总结 1.引言 C三剑客之s…...
)
【C语言】8.C语言操作符详解(2)
文章目录 6.单⽬操作符7.逗号表达式8.下标访问[]、函数调⽤()8.1 [ ] 下标引⽤操作符8.2 函数调⽤操作符 9.结构成员访问操作符9.1 结构体9.1.1 结构的声明9.1.2 结构体变量的定义和初始化 9.2 结构成员访问操作符9.2.1 结构体成员的直接访问9.2.2 结构体成员的间接访问 6.单⽬…...

vivado 物理约束KEEP_HIERARCHY
KEEP_HIERARCHY Applied To Cells Constraint Values • TRUE • FALSE • YES • NO UCF Example INST u1 KEEP_HIERARCHY TRUE; XDC Example set_property DONT_TOUCH true [get_cells u1] IOB Applied To Cells Constraint Values IOB_XnYn UCF Examp…...

Linux 三十六章
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C,linux 🔥座右铭:“不要…...

ntsd用法+安装包
ntsd是一个强大的进程终止软件,除了少数系统进程之外一律杀掉 用法 1.ntsd -c q -p 进程的pid 2.ntsd -c q -pn 进程名 记得解压到System32里面 当然,资源管理器的进程是可以杀的所以也可以让电脑黑屏 同样可以让电脑黑屏的还有taskkill /f /im 进程…...

Nacos 微服务管理
Nacos 本教程将为您提供Nacos的基本介绍,并带您完成Nacos的安装、服务注册与发现、配置管理等功能。在这个过程中,您将学到如何使用Nacos进行微服务管理。下方是官方文档: Nacos官方文档 1. Nacos 简介 Nacos(Naming and Confi…...
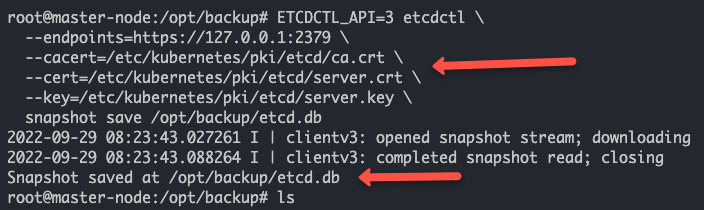
Kubernetes集群上的Etcd备份和恢复
在本教程中,您将学习如何在Kubernetes集群上使用etcd快照进行etcd备份和恢复。 在Kubernetes架构中,etcd是集群的重要组成部分。所有集群对象及其状态都存储在etcd中。为了更好地理解Kubernetes,有几点关于etcd的信息是您需要了解的。 它是…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
