零基础代码随想录【Day42】|| 1049. 最后一块石头的重量 II,494. 目标和,474.一和零
目录
DAY42
1049.最后一块石头的重量II
解题思路&代码
494.目标和
解题思路&代码
474.一和零
解题思路&代码
DAY42
1049.最后一块石头的重量II
力扣题目链接(opens new window)
题目难度:中等
有一堆石头,每块石头的重量都是正整数。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下,就返回 0。
示例:
- 输入:[2,7,4,1,8,1]
- 输出:1
解释:
- 组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
- 组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
- 组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
- 组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
本题就和 昨天的 416. 分割等和子集 很像了,可以尝试先自己思考做一做。
视频讲解:动态规划之背包问题,这个背包最多能装多少?LeetCode:1049.最后一块石头的重量II_哔哩哔哩_bilibili
代码随想录
解题思路&代码
思路:
关键点:认识到什么是应用类背包问题,此处如何联系到背包?尽量把容器分成大小相等的两堆,则另一堆是否能用数组元素填满多少则是涉及到了背包最多能装多少的问题
本题其实就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。
是不是感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。
本题物品的重量为stones[i],物品的价值也为stones[i]。
对应着01背包里的物品重量weight[i]和 物品价值value[i]。
1.确定dp数组以及下标的含义
dp[j]表示容量(这里说容量更形象,其实就是重量)为j的背包,最多可以背最大重量为dp[j]。
可以回忆一下01背包中,dp[j]的含义,容量为j的背包,最多可以装的价值为 dp[j]。
2.确定递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题则是:dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
3.dp数组如何初始化
既然 dp[j]中的j表示容量,那么最大容量(重量)是多少呢,就是所有石头的重量和。
因为提示中给出1 <= stones.length <= 30,1 <= stones[i] <= 1000,所以最大重量就是30 * 1000 。
而我们要求的target其实只是最大重量的一半,所以dp数组开到15000大小就可以了
4.确定遍历顺序
在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中就已经说明:如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
- 时间复杂度:O(m × n) , m是石头总重量(准确的说是总重量的一半),n为石头块数
- 空间复杂度:O(m)
class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0;for (int i : stones) {sum += i;}int target = sum >> 1;//初始化dp数组int[] dp = new int[target + 1];//为什么要+1,因为涉及到背包重量为0的情况,要初始化,但是实际上数组元素是不包括这个的for (int i = 0; i < stones.length; i++) {//采用倒序for (int j = target; j >= stones[i]; j--) {//两种情况,要么放,要么不放dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[target];}
}494.目标和
力扣题目链接(opens new window)
难度:中等
给定一个非负整数数组,a1, a2, ..., an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
示例:
- 输入:nums: [1, 1, 1, 1, 1], S: 3
- 输出:5
解释:
- -1+1+1+1+1 = 3
- +1-1+1+1+1 = 3
- +1+1-1+1+1 = 3
- +1+1+1-1+1 = 3
- +1+1+1+1-1 = 3
一共有5种方法让最终目标和为3。
大家重点理解 递推公式:dp[j] += dp[j - nums[i]],这个公式后面的提问 我们还会用到。
视频讲解:动态规划之背包问题,装满背包有多少种方法?| LeetCode:494.目标和_哔哩哔哩_bilibili
代码随想录
解题思路&代码
思路:
本题要如何使表达式结果为target,
既然为target,那么就一定有 left组合 - right组合 = target。
left + right = sum,而sum是固定的。right = sum - left
公式来了, left - (sum - left) = target 推导出 left = (target + sum)/2 。
target是固定的,sum是固定的,left就可以求出来。
此时问题就是在集合nums中找出和为left的组合
再回归到01背包问题,为什么是01背包呢?
因为每个物品(题目中的1)只用一次!
这次和之前遇到的背包问题不一样了,之前都是求容量为j的背包,最多能装多少。
本题则是装满有几种方法。其实这就是一个组合问题了。
1.确定dp数组以及下标的含义
dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法
其实也可以使用二维dp数组来求解本题,dp[i][j]:使用 下标为[0, i]的nums[i]能够凑满j(包括j)这么大容量的包,有dp[i][j]种方法。
2.确定递推公式
有哪些来源可以推出dp[j]呢?
只要搞到nums[i],凑成dp[j]就有dp[j - nums[i]] 种方法。
例如:dp[j],j 为5,
- 已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 容量为5的背包。
- 已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 容量为5的背包。
- 已经有一个3(nums[i]) 的话,有 dp[2]中方法 凑成 容量为5的背包
- 已经有一个4(nums[i]) 的话,有 dp[1]中方法 凑成 容量为5的背包
- 已经有一个5 (nums[i])的话,有 dp[0]中方法 凑成 容量为5的背包
那么凑整dp[5]有多少方法呢,也就是把 所有的 dp[j - nums[i]] 累加起来。
所以求组合类问题的公式,都是类似这种:
dp[j] += dp[j - nums[i]]3.dp数组如何初始化
从递推公式可以看出,在初始化的时候dp[0] 一定要初始化为1,因为dp[0]是在公式中一切递推结果的起源,如果dp[0]是0的话,递推结果将都是0。
如果数组[0] ,target = 0,那么 bagSize = (target + sum) / 2 = 0。 dp[0]也应该是1, 也就是说给数组里的元素 0 前面无论放加法还是减法,都是 1 种方法。
所以本题我们应该初始化 dp[0] 为 1。
4.确定遍历顺序
在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中,我们讲过对于01背包问题一维dp的遍历,nums放在外循环,target在内循环,且内循环倒序。
5.举例推导dp数组
输入:nums: [1, 1, 1, 1, 1], S: 3
bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:

- 时间复杂度:O(n × m),n为正数个数,m为背包容量
- 空间复杂度:O(m),m为背包容量
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int i = 0; i < nums.length; i++) sum += nums[i];//如果target的绝对值大于sum,那么是没有方案的if (Math.abs(target) > sum) return 0;//如果(target+sum)除以2的余数不为0,也是没有方案的if ((target + sum) % 2 == 1) return 0;int bagSize = (target + sum) / 2;int[] dp = new int[bagSize + 1];dp[0] = 1;for (int i = 0; i < nums.length; i++) {for (int j = bagSize; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[bagSize];}
}474.一和零
力扣题目链接(opens new window)
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的大小,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
-
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
-
输出:4
-
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。 其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
通过这道题目,大家先粗略了解, 01背包,完全背包,多重背包的区别,不过不用细扣,因为后面 对于 完全背包,多重背包 还有单独讲解。
视频讲解:动态规划之背包问题,装满这个背包最多用多少个物品?| LeetCode:474.一和零_哔哩哔哩_bilibili
代码随想录
解题思路&代码
思路:
本题并不是多重背包,再来看一下这个图,捋清几种背包的关系
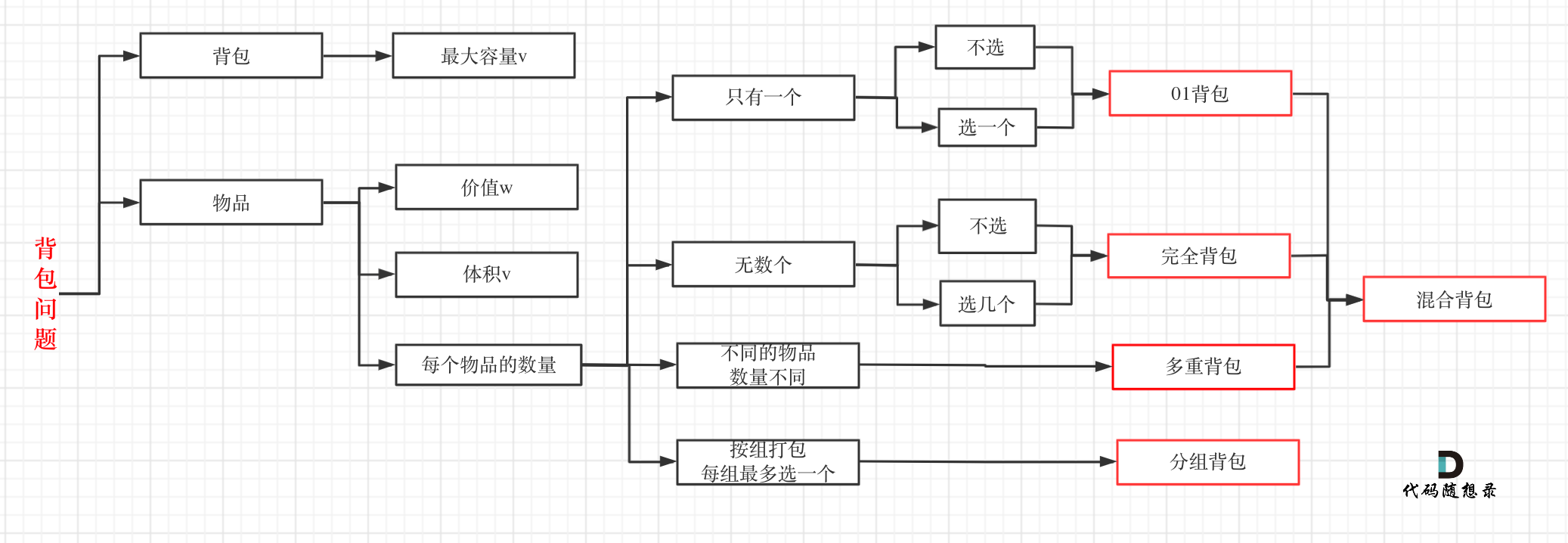
多重背包是每个物品,数量不同的情况。
本题中strs 数组里的元素就是物品,每个物品都是一个!
而m 和 n相当于是一个背包,两个维度的背包。
理解成多重背包的同学主要是把m和n混淆为物品了,感觉这是不同数量的物品,所以以为是多重背包。
但本题其实是01背包问题!
只不过这个背包有两个维度,一个是m 一个是n,而不同长度的字符串就是不同大小的待装物品。
1.确定dp数组(dp table)以及下标的含义
dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
2.确定递推公式
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。
dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
然后我们在遍历的过程中,取dp[i][j]的最大值。
所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
此时大家可以回想一下01背包的递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
对比一下就会发现,字符串的zeroNum和oneNum相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])。
这就是一个典型的01背包! 只不过物品的重量有了两个维度而已。
3.dp数组如何初始化
在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中已经讲解了,01背包的dp数组初始化为0就可以。
因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖。
4.确定遍历顺序
在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中,我们讲到了01背包为什么一定是外层for循环遍历物品,内层for循环遍历背包容量且从后向前遍历!
那么本题也是,物品就是strs里的字符串,背包容量就是题目描述中的m和n。
- 时间复杂度: O(kmn),k 为strs的长度
- 空间复杂度: O(mn)
class Solution {public int findMaxForm(String[] strs, int m, int n) {//dp[i][j]表示i个0和j个1时的最大子集int[][] dp = new int[m + 1][n + 1];int oneNum, zeroNum;for (String str : strs) {//正序遍历物品oneNum = 0;zeroNum = 0;for (char ch : str.toCharArray()) {if (ch == '0') {zeroNum++;} else {oneNum++;}}//倒序遍历背包容量for (int i = m; i >= zeroNum; i--) {for (int j = n; j >= oneNum; j--) {dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
}相关文章:

零基础代码随想录【Day42】|| 1049. 最后一块石头的重量 II,494. 目标和,474.一和零
目录 DAY42 1049.最后一块石头的重量II 解题思路&代码 494.目标和 解题思路&代码 474.一和零 解题思路&代码 DAY42 1049.最后一块石头的重量II 力扣题目链接(opens new window) 题目难度:中等 有一堆石头,每块石头的重量都是正整…...

2024-5-24 石群电路-15
2024-5-24,星期五,22:15,天气:晴,心情:晴。今天最后一天上班,终于要放返校假啦,开心!!!!!!不过放假也不能耽误…...

功能测试:核心原理、挑战以及解决之道
在软件开发生命周期中,功能测试占据了至关重要的位置。它是确保软件应用按照既定的要求和规格运行的关键测试阶段。功能测试的目的在于验证软件的功能、行为和用户界面等是否达到了业务需求的标准。本文将深入探讨功能测试的概念,执行过程中可能遇到的挑…...

跨境电商赛道,云手机到底能不能化繁为简?
当下国内电商背景: 从零售额的数据来看:随着互联网的普及和消费者购物习惯的改变,国内电商市场规模持续扩大。据相关数据显示,网络消费亮点纷呈,一季度全国网上零售额达到了3.3万亿元,同比增长12.4%。这表…...
linux:信号深入理解
文章目录 1.信号的概念1.1基本概念1.2信号的处理基本概念1.3信号的发送与保存基本概念 2.信号的产生2.1信号产生的五种方式2.2信号遗留问题(core,temp等) 3.信号的保存3.1 信号阻塞3.2 信号特有类型 sigset_t3.3 信号集操作函数3.4 信号集操作函数的使用 4.信号的处理4.1 信号的…...

Android系统的/etc/mkshrc文件
/etc/mkshrc 文件是用于配置 mksh(MirBSD Korn Shell)环境的启动脚本。mksh 是 Android 默认使用的 shell,在 shell 启动时会读取并执行这个文件中的配置。以下是关于 /etc/mkshrc 文件的详细信息及其用途。 /etc/mkshrc 文件的作用 环境配…...
LeetCode199二叉树的右视图
题目描述 给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。 解析 这一题的关键其实就是找到怎么去得到当前是哪一层级,可以利用队列对二叉树进行层次遍历,但…...

JavaScript 基础
一 JavaScript 的书写形式 1.1 行内式 <input type"button" value"点我一下" onclick"alert(hello akai);" > 注意,JS 中的字符串常量可以用单引号表示,也可以使用双引号表示.HTML 中推荐使用双引号,JS 中推荐使用单引号(使用双引号容易…...

DOS学习-目录与文件应用操作经典案例-type
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一.前言 二.使用 三.案例 1. 查看文本文件内容 2. 同时查看多个文本文件内容 3. 合并文…...

QT教程-一,初识QT
目录 一,QT是什么?能够使用它做什么? 二,Qt 能够使用的语言 三,Qt主要用于什么领域? 四,Qt开发的软件 一,QT是什么?能够使用它做什么? Qt是一个跨平台的 C 开发库,主…...

SpringBoot搭建Eureka注册中心
系列文章目录 文章目录 系列文章目录前言前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看懂了就去分享给你的码吧。 1、Spring-Cloud Euraka介绍 Spring-Cloud Euraka是Spring Cloud集合中一…...
day 38 435.无重叠区间 763.划分字母区间 56. 合并区间 738.单调递增的数字 968.监控二叉树
435.无重叠区间 思路 为了使区间尽可能的重叠所以排序来使区间尽量的重叠,使用左边界排序来统计重叠区间的个数与452. 用最少数量的箭引爆气球恰好相反。 代码 class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals,(a,…...
ssm/springoot养老院问诊服务预约系统_96316老年人服务系统
2.管理员: (1)登入注册页面:管理员进行操作时需要是已注册登入的 (2)权限管理:管理员登入后可以运用权限进行相应的操作管理。 (3)用户管理:对用户进行删除、…...

WordPress插件优化对提升性能有多大影响?
WordPress插件优化对提升性能的影响可以是非常显著的。插件是WordPress平台的一个重要组成部分,它们可以增强网站的功能和定制性。然而,如果插件没有经过优化,它们可能会成为网站性能的瓶颈。 通过优化插件,可以减少对服务器资源…...
Servlet的response对象
目录 HTTP响应报文协议 reponse继承体系 reponse的方法 响应行 public void setStatus(int sc) 响应头 public void setHeader(String name, String value) 响应体 public java.io.PrintWriter getWriter() public ServletOutputStream getOutputStream() 请求重定…...

Unity射击游戏开发教程:(20)增加护盾强度
在本文中,我们将增强护盾,使其在受到超过 1 次攻击后才会被禁用。 Player 脚本具有 Shield PowerUp 方法,我们需要调整盾牌在被摧毁之前可以承受的数量,因此我们将声明一个 int 变量来设置盾牌可以承受的击中数量。...

初识C语言——第二十八天
代码练习1: 用函数的方式实现9*9乘法表 void print_table(int n) {int i 0;int j 0;for (i 1; i< n; i){for (j 1; j< i; j){printf("%d*%d%-3d ", i, j, i * j);}printf("\n");}}int main() {int n 0;scanf("%d", &a…...
输入事件分发到Native层的流程)
Android NDK系列(三)输入事件分发到Native层的流程
在Android NDK系列(一)手动搭建Native Project 创建的Native工程中,是可以接收输入事件的,只需在android_main中注册输入事件的处理函数,当触摸屏幕后,handleInputEvent函数便会调用,代码如下。 static int32_t handleInputEvent(struct android_app* app, AInputEvent…...
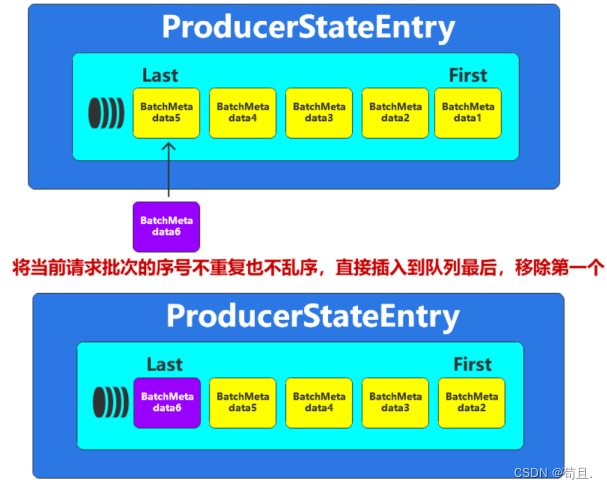
Kafka之【生产消息】
消息(Record) 在kafka中传递的数据我们称之为消息(message)或记录(record),所以Kafka发送数据前,需要将待发送的数据封装为指定的数据模型: 相关属性必须在构建数据模型时指定,其中…...
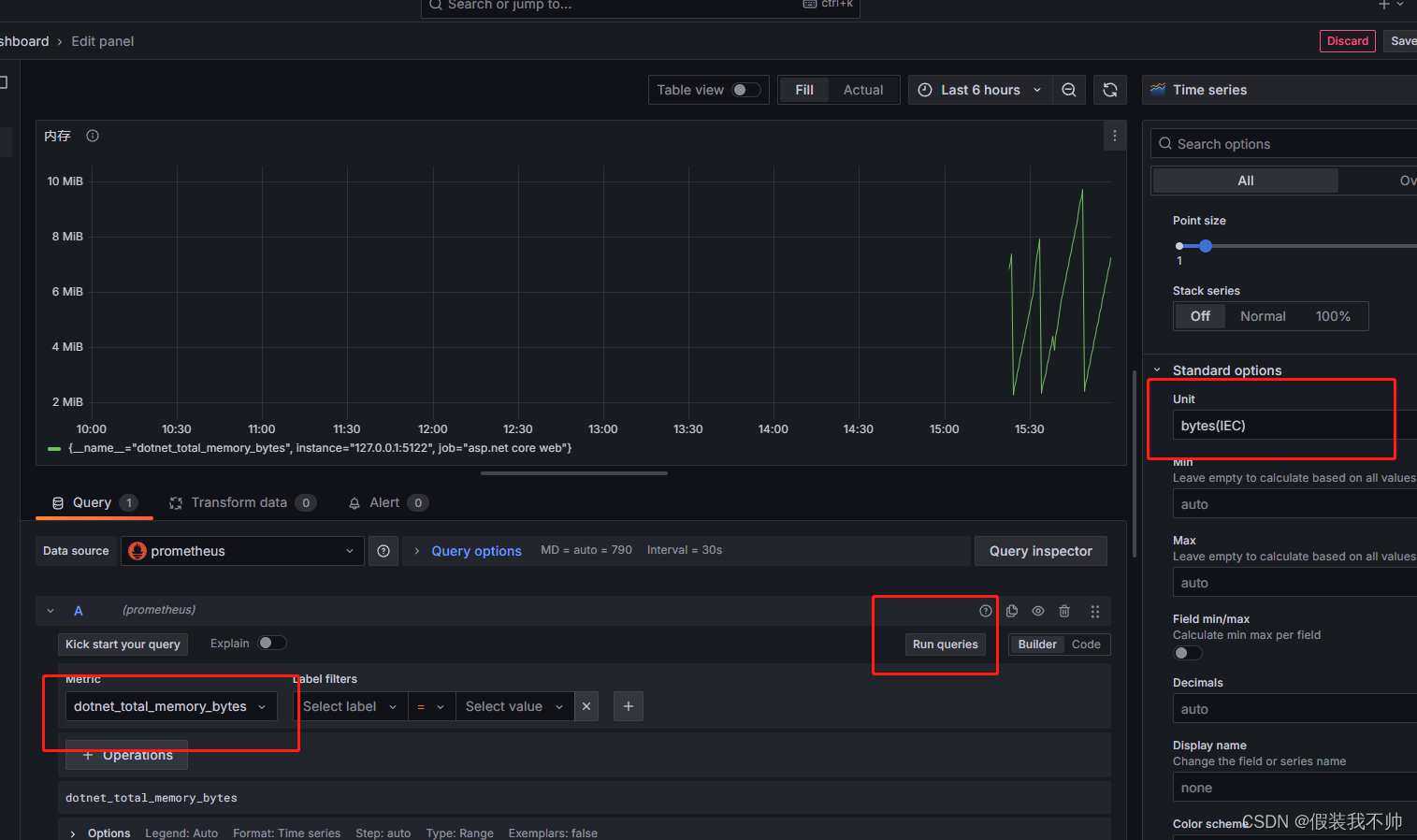
asp.net core接入prometheus
安装prometheus和Grafana 参考之前的文章->安装prometheus和Grafana教程 源代码 dotnet源代码 新建.net core7 web项目 修改Program.cs using Prometheus;namespace PrometheusStu01;public class Program {public static void Main(string[] args){var builder We…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...
