作业39 sqrt应用
目录
判断完全平方数
题目描述
输出所有因数
题目描述
因子求和
题目描述
判断素数
题目描述
判断完全平方数
题目描述
输入一个整数,判断他是否是完全平方数,如果是,输出yes,否则输出no
样例 样例 样例
输入复制 输入复制 输入复制
9 100 80
输出复制 输出复制 输出复制
yes yes no
#include<iostream>
#include<cmath>
#include<string.h>
using namespace std;
int main()
{int n;cin>>n;if((int)sqrt(n) == sqrt(n)){cout<<"yes";}else{cout<<"no"; }return 0;
}输出所有因数
题目描述
输入一个整数,输出他的所有因数(除了1和它本身)空格隔开
样例 样例
输入复制 输入复制
100 30
输出复制 输出复制
2 50 4 25 5 20 10 2 15 3 10 5 6
#include<iostream>
#include<cmath>
#include<string.h>
using namespace std;
int main()
{int n;cin>>n;for(int i = 1;i<=n-1;i++){for(int j = 2;j<=sqrt(i);j++){if(i%j == 0){cout<<i<<" "<<j;}}}return 0;
}因子求和
题目描述
已知一个正整数N(20 <= N <= 800000000)
请你编写程序求出该数的全部因子(不包括1和n)的和。
输入 样例 样例
一个正整数n。 输入复制 输入复制
输出 24 9
一个整数代表n的因子和。 输出复制 输出复制
35 3
#include<iostream>
#include<cmath>
#include<string.h>
using namespace std;
int main()
{int n;cin>>n;int sum = 0;for(int i = 1;i<=n-1;i++){for(int j = 2;j<=sqrt(i);j++){if(i%j == 0){sum = sum + j;}}}cout<<sum;return 0;
}判断素数
题目描述
任意输入一个整数,判断它是否为素数。是的话输出"T",不是的话输出"F".
质数(prime number)又称素数,质数定义为在大于1的自然数中,除了1和它本身以外不再有其他因数。
输入 样例
输入只有一行,包括1个整数。(n≤109) 输入复制
输出 57
输出只有一行。 输出复制
F
#include<iostream>
#include<cmath>
#include<string.h>
using namespace std;
int main()
{int n;cin>>n;for(int i = 2;i<=sqrt(n);i++){if(n%i == 0){cout<<"T";return 0;}}cout<<"F";return 0;
}相关文章:

作业39 sqrt应用
目录 判断完全平方数 题目描述 输出所有因数 题目描述 因子求和 题目描述 判断素数 题目描述 判断完全平方数 题目描述 输入一个整数,判断他是否是完全平方数,如果是,输出yes,否则输出no 样例 样例…...

springboot 实现跨域的几种方式
1、跨域的原因: 由于同源策略(Same Origin Policy)的限制,浏览器不允许跨域请求。同源策略规定,A网页设置的Cookie、LocalStorage和IndexDB无法被同源以外的网页读取。 2、原因: 1)浏览器的同源策略(Same Origin Policy)限制了跨域请求。主要…...
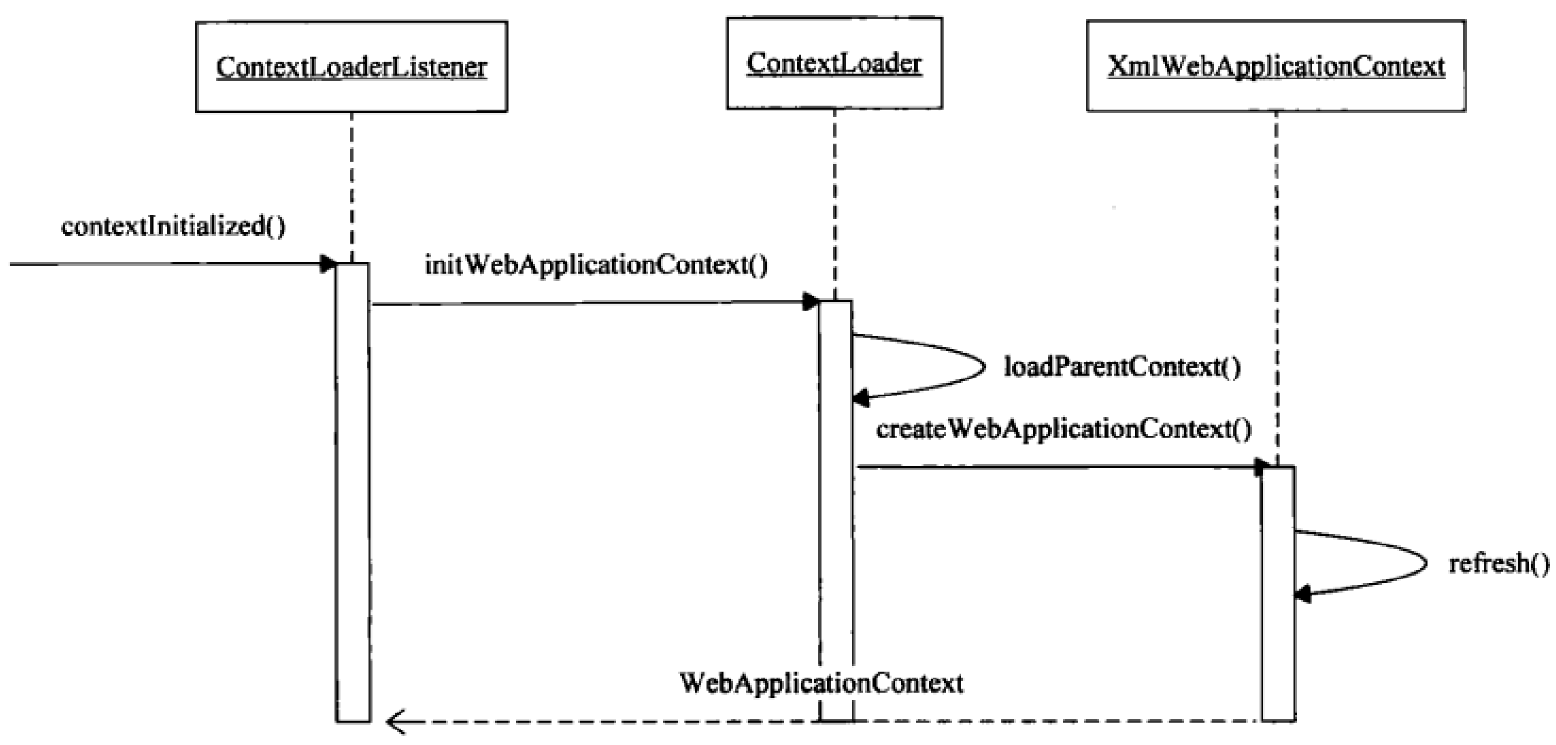
springmvc Web上下文初始化
Web上下文初始化 web上下文与SerlvetContext的生命周期应该是相同的,springmvc中的web上下文初始化是由ContextLoaderListener来启动的 web上下文初始化流程 在web.xml中配置ContextLoaderListener <listener> <listener-class>org.springframework.…...

Verilog实战学习到RiscV - 2 : wire 和 reg 的区别
Verilog: wire 和 reg 的区别 1 引言 看Verilog例子过程中,总是分不清 wire 和 reg 的区别。这篇文章把两者放在一起总结一下,并且对比何时使用它们。 1.1 wire :组合逻辑 wire 是 Verilog 设计中的简单导线(或任意宽度的总线…...

OpenGL给定直线起点和终点不同的颜色,使用中点Bresenham画线
用鼠标左键按下确定直线起点,鼠标左键抬起确定直线终点。放一部分代码。 // 中点Bresenham算法.cpp : 定义控制台应用程序的入口点。 //#include "stdafx.h" #include <GL/glut.h> #include <iostream> #include <cmath>int windowWidt…...

IT行业的现状与未来发展趋势:从云计算到量子计算的技术变革
随着技术的不断进步,IT行业已经成为推动全球经济和社会发展的关键力量。从云计算、大数据、人工智能到物联网、5G通信和区块链,这些技术正在重塑我们的生活和工作方式。本文将深入探讨当前IT行业的现状,并展望未来发展趋势,旨在为…...
电脑远程控制另一台电脑怎么弄?
可以远程控制另一台电脑吗? “你好,我对远程访问技术不太了解。现在,我希望我的朋友可以远程控制我的Windows 10电脑,以便她能帮我解决一些问题。请问,有没有免费的方法可以实现这种远程控制?我该如何操作…...
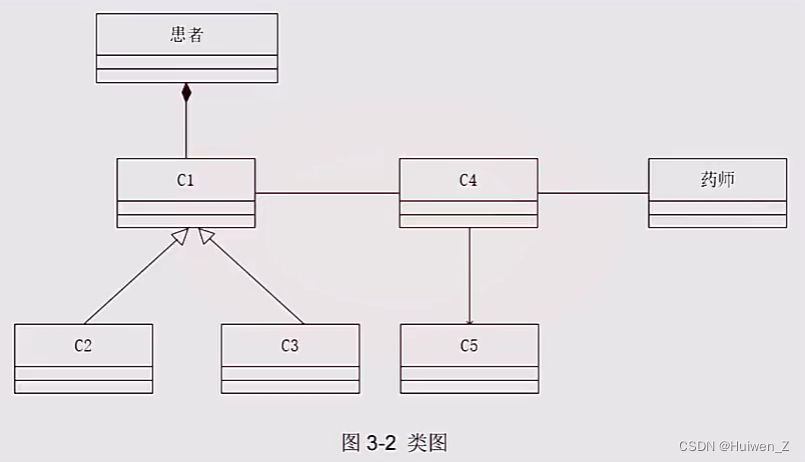
软件设计师备考 | 案例专题之面向对象设计 概念与例题
相关概念 关系 依赖:一个事物的语义依赖于另一个事物的语义的变化而变化 关联:一种结构关系,描述了一组链,链是对象之间的连接。分为组合和聚合,都是部分和整体的关系,其中组合事物之间关系更强。两个类之…...

UniApp 2.0可视化开发工具:引领前端开发新纪元
一、引言 在移动互联网迅猛发展的今天,移动应用开发已经成为前端开发的重要方向之一。为了简化移动应用开发流程,提高开发效率,各大开发平台不断推出新的工具和框架。UniApp作为一款跨平台的移动应用开发框架,自诞生以来就备受开…...
)
前端调用浏览器录音功能且生成文件(vue)
如果可以实现记得点赞分享,谢谢老铁~ 首先在页面中给两个按钮,分别是“开始录音”,“结束录音”。以及录音成功后生成一个下载语音的链接。 1. 先看页面展示 <template><div><button click"startRecording…...

「大数据」Kappa架构
Kappa架构是一种处理大数据的架构,它作为Lambda架构的替代方案出现。Kappa架构的核心思想是简化数据处理流程,通过使用单一的流处理层来同时处理实时和批量数据,从而避免了Lambda架构中需要维护两套系统(批处理层和速度层…...

详细分析Element Plus中的ElMessageBox弹窗用法(附Demo及模版)
目录 前言1. 基本知识2. Demo3. 实战4. 模版 前言 由于需要在登录时,附上一些用户说明书的弹窗 对于ElMessageBox的基本知识详细了解 可通过官网了解基本的语法知识ElMessageBox官网基本知识 1. 基本知识 Element Plus 是一个基于 Vue 3 的组件库,其中…...
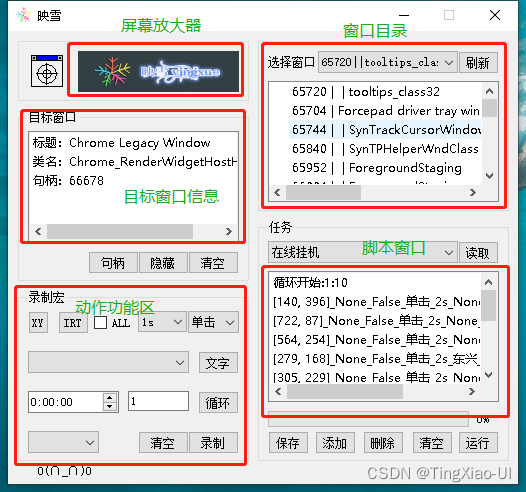
Python自动化工具(桌面自动化、Web自动化、游戏辅助)
工具介绍 连点工具是一款可以模拟键鼠后台操作的连点器工具。支持鼠标连点、键鼠脚本录制,支持辅助您实现办公自动化以及辅助游戏操作。功能简洁易用,非常方便操作。连点工具让您在在玩游戏、网购抢购的时候全自动点击鼠标!主要功能有&#…...

opencv进阶 ——(五)图像处理之马赛克
一、遍历图像并对每个马赛克区域进行像素化处理 for (int y 0; y < image.rows; y blockSize) {for (int x 0; x < image.cols; x blockSize) {cv::Rect rect cv::Rect(x, y, std::min(blockSize, image.cols - x), std::min(blockSize, image.rows - y));cv::Scal…...

电机控制系列模块解析(22)—— 零矢量刹车
一、零矢量刹车 基本概念 逆变器通常采用三相桥式结构,包含六个功率开关元件(如IGBT或MOSFET),分为上桥臂和下桥臂。每个桥臂由两个反并联的开关元件组成,上桥臂和下桥臂对应于电机三相绕组的正负端。正常工作时&…...

自定义一个SpringBoot场景启动器
前言 一个刚刚看完SpringBoot自动装配原理的萌新依据自己的理解写下的文章,如有大神发现错误,敬请斧正,不胜感激。 分析SpringBoot自动配置原理 SpringBoot的启动从被SpringBootApplication修饰的启动类开始,SpringBootApplicaiotn注解中最…...

UDP的报文结构和注意事项
UDP协议是在传输层的协议。 UDP无连接,不可靠传输,面向数据报,全双工。 UDP的报文结构 学习网络协议,最主要的就是报文格式。 对于UDP来说,应用层的数据到达,UDP之后,就会给应用层的数据报前面…...

rust语言一些规则学习
目录 rust中迭代器的使用(iter().map()与for循环的区别)map()与for的描述区别总结 最后更新时间2024-05-24 rust中迭代器的使用(iter().map()与for循环的区别) map()与for的描述 rust源码中关于iter().map()函数的解释ÿ…...

QML基本语法介绍
为什么使用QML 开发者效率 将前后端分离,QML和JavaScript语言主要用于前度UI的方法,后端有C++来完成绘制。将JavaScript和C++分开能够快速迭代开发; 跨平台移植性 基于Qt平台的统一抽象概念,现在可以更加容易和快速和将Qt移植到更多的平台上。 开发的开放 Qt是由Qt-Proje…...
)
学习和分享关于 Vue.js 的路由(vue-router)
学习和分享关于 Vue.js 的路由(vue-router)是一个非常有价值的主题,因为路由是构建单页应用程序(SPA)的核心部分。本文将介绍 Vue.js 路由的基本概念和实现,并展示一个典型的项目目录结构。 目录 Vue.js 路…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...
