蓝桥杯-暴力搜索BFS+DFS
九九乘法表挂毯
问题描述:
在一个古老的城堡里,一位名为 Alex 的少年发现了一幅巨大的九九乘法表挂毯。挂毯被划分成了9x9的方格,每个方格上写着相应的乘积。Alex 想象自己站在数值为1的方格上,他的目标是到达数值为 81 的方格。然而,少年遵循着一项规则:他只能移动到数值为 1、81 或任意偶数的相邻方格上。城堡的图书管理员告诉他,只有找到最短路径到达目标,他才能解开挂毯的秘密。
请你帮助 Alex计算,在遵循上述移动规则的情况下,他从1到81的最短路径有多少种可能。
输入格式
无。
输出格式
输出一个整数,表示从1到 81 的最短路径的可能数量。
题目分析:
这道题深度的考验BFS和DFS的综合运用,可以作为考验自己是否对这两种算法熟悉的一道题去练练手,下方配py的题解,仅供参考。
综合思路就是,先用BFS求出最短路径是多少,然后用DFS去求符合该步数的路径有多少条。
代码实现:
m=[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
[0, 2, 4, 6, 8, 10, 12, 14, 16, 18],
[0, 3, 6, 9, 12, 15, 18, 21, 24, 27],
[0, 4, 8, 12, 16, 20, 24, 28, 32, 36],
[0, 5, 10, 15, 20, 25, 30, 35, 40, 45],
[0, 6, 12, 18, 24, 30, 36, 42, 48, 54],
[0, 7, 14, 21, 28, 35, 42, 49, 56, 63],
[0, 8, 16, 24, 32, 40, 48, 56, 64, 72],
[0, 9, 18, 27, 36, 45, 54, 63, 72, 81]]dirs=[[0,1],[0,-1],[-1,0],[1,0]] #四条路
def bfs(m):st,ed=[1,1],[9,9]stack=[[st,0]]while stack:curnode,step=stack.pop(0)print(curnode)if curnode==ed: return stepstep+=1for i in dirs:a0,a1=curnode[0]+i[0],curnode[1]+i[1]if 9>=a0>0 and 9>=a1>0 and (m[a0][a1] %2==0 or m[a0][a1]==81):newnode=[a0,a1]stack.append([newnode,step])m[a0][a1]=1
print(bfs(m))res=0
def dfs(x,y,key,step):global resif step>16: returnif key==81:res+=1returnelse:for dir in dirs:x0,y0=x+dir[0],y+dir[1]if 9>=x0>0 and 9>=y0>0 and (m[x0][y0]%2==0 or m[x0][y0]==81):v=m[x0][y0]dfs(x0,y0,v,step+1)
dfs(1,1,1,0)
print(res)题目总结:
这种题目主要考察对DFS和BFS两种搜索算法的理解和运用能力。所以要求我们必须掌握以下内容:
-
理解DFS和BFS的基本原理:DFS是深度优先搜索算法,从起始节点开始,沿着一条路径一直往下搜索直到无法继续为止,然后返回上一个节点继续搜索;BFS是广度优先搜索算法,从起始节点开始,先搜索所有相邻节点,再逐层向下搜索。
-
分析DFS和BFS的应用场景:DFS通常用于寻找所有可能的解或路径,适用于图的遍历、拓扑排序、连通性检测等问题;BFS通常用于求最短路径、最小步数等问题。
-
比较DFS和BFS的特点:DFS递归实现简单,但可能会无限循环;BFS借助队列实现,保证了最优解,但空间复杂度较高。
-
实际应用中如何选择DFS和BFS:根据具体问题特点选择合适的搜索算法,通常情况下,如果需要找到解的所有可能,可以使用DFS;如果要求最短路径或步数,可以使用BFS。
相关文章:

蓝桥杯-暴力搜索BFS+DFS
九九乘法表挂毯 问题描述: 在一个古老的城堡里,一位名为 Alex 的少年发现了一幅巨大的九九乘法表挂毯。挂毯被划分成了9x9的方格,每个方格上写着相应的乘积。Alex 想象自己站在数值为1的方格上,他的目标是到达数值为 81 的方格。…...
)
巧用count与count()
在C#中,talentInnoPfChains.Count() 和 talentInnoPfChains.Count 的性能差异主要取决于 talentInnoPfChains 的类型。这里有两种可能的情况: 如果 talentInnoPfChains 是一个实现了 ICollection<T> 接口的集合(如 List<T>, Hash…...

MongoDB 覆盖索引查询:提升性能的完整指南
MongoDB 覆盖索引查询是一种优化数据库查询性能的技术,它通过创建适当的索引,使查询可以直接从索引中获取所需的数据,而无需访问实际的文档数据。这种方式可以减少磁盘 I/O 和内存消耗,提高查询性能。 基本语法 在 MongoDB 中&a…...

ECMAScript详解
ECMAScript(简称ES)是一种由Ecma国际(前身为欧洲计算机制造商协会,European Computer Manufacturers Association)通过ECMA-262标准化的脚本程序设计语言。以下是对ECMAScript的详细说明: 1. 定义与起源 …...
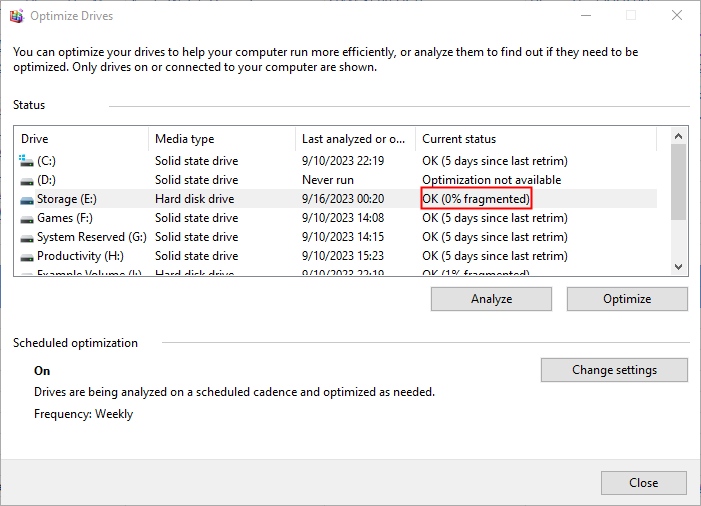
如何在Windows 10上对硬盘进行碎片整理?这里提供步骤
随着时间的推移,由于文件系统中的碎片,硬盘驱动器可能会开始以较低的效率运行。为了加快驱动器的速度,你可以使用内置工具在Windows 10中对其进行碎片整理和优化。方法如下。 什么是碎片整理 随着时间的推移,组成文件的数据块&a…...

科学高效备考AMC8和AMC10竞赛,吃透2000-2024年1850道真题和解析
多做真题,吃透真题和背后的知识点是备考AMC8、AMC10有效的方法之一,通过做真题,可以帮助孩子找到真实竞赛的感觉,而且更加贴近比赛的内容,可以通过真题查漏补缺,更有针对性的补齐知识的短板。 今天我们继续…...

SQL——SELECT相关的题目
目录 197、上升的温度 577、员工奖金 586、订单最多的客户 596、超过5名学生的课 610、判断三角形 620、有趣的电影 181、超过经理收入的员工 1179、重新格式化部门表(行转列) 1280、学生参加各科测试的次数 1068、产品销售分析I 1075、项目员工I …...

etcd集群部署
1.etcd介绍 1.1 什么是etcd etcd的官方定义如下: A distributed, reliable key-value store for the most critical data of distributed systemetcd是一个Go语言编写的分布式、高可用的一致性键值存储系统,用于提供可靠的分布式键值(key value)存储、配置共享和服务发现等…...

VBA_MF系列技术资料1-615
MF系列VBA技术资料1-615 为了让广大学员在VBA编程中有切实可行的思路及有效的提高自己的编程技巧,我参考大量的资料,并结合自己的经验总结了这份MF系列VBA技术综合资料,而且开放源码(MF04除外),其中MF01-0…...

常用激活函数学习
常用激活函数及其应用 ReLU (Rectified Linear Unit) 公式: f ( x ) max ( 0 , x ) f(x) \max(0, x) f(x)max(0,x)理解: 当输入值为正时,输出等于输入值;否则输出为0。ReLU函数简单且计算效率高,能有效缓解梯度消失问题,促进…...

html中被忽略的简单标签
1: alt的作用是在图片不能显示时的提示信息 <img src"https://img.xunfei.cn/mall/dev/ifly-mall-vip- service/business/vip/common/202404071019208761.jp" alt"提示信息" width"100px" height"100px" /> 2&#…...
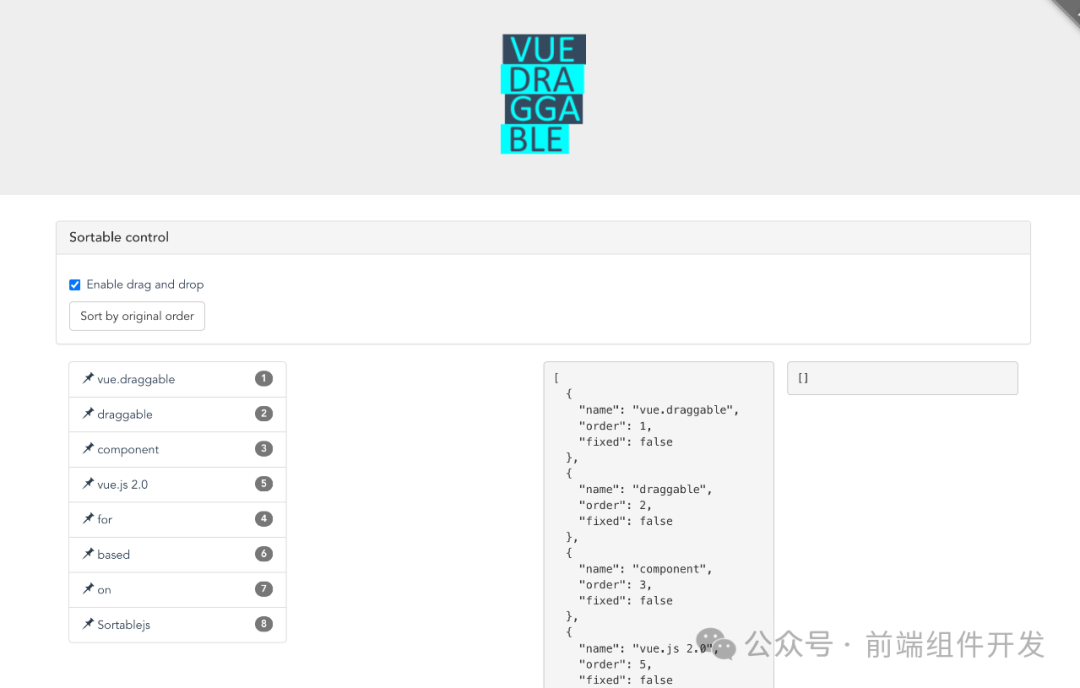
Vue.Draggable:强大的Vue拖放组件技术探索
一、引言 随着前端技术的不断发展,拖放(Drag-and-Drop)功能已经成为许多Web应用不可或缺的一部分。Vue.js作为现代前端框架的佼佼者,为开发者提供了丰富的生态系统和强大的工具链。Vue.Draggable作为基于Sortable.js的Vue拖放组件…...

linux mail命令及其历史
一、【问题描述】 最近隔壁组有人把crontab删了,crontab这个命令有点反人类,它的参数特别容易误操作: crontab - 是删除计划表 crontab -e 是编辑,总之就是特别容易输入错误。 好在可以通过mail命令找回,但是mai…...
和以数据为中心(Data-Centric)的区别)
数据驱动(Data-Driven)和以数据为中心(Data-Centric)的区别
一、什么是数据驱动? 数据驱动(Data-Driven)是在管理科学领域经常提到的名词。数据驱动决策(Data-Driven Decision Making,简称DDD)是一种方法论,即在决策过程中主要依赖于数据分析和解释&…...

aosp14的分屏接口ISplitScreen接口获取方式更新-学员疑问答疑
背景: 有学员朋友在学习马哥的分屏pip自由窗口专题时候,做相关分屏做小桌面项目时候,因为原来课程版本是基于android 13进行的讲解的,但是现在公司已经开始逐渐进行相关的android 14的适配了,但是android 14这块相比a…...
定积分求解过程是否变限问题 以及当换元时注意事项
目录 定积分求解过程是否变限问题 文字理解: 实例理解: 易错点和易混点: 1:定积分中的换元指什么? 2: 不定积分中第一类换元法和第二类换元法的本质和区别 3: df(x) ----> df(x)这…...
)
保研机试算法训练个人记录笔记(七)
输入格式: 在第1 行给出不超过10^5 的正整数N, 即参赛}人数。随后N 行,每行给出一位参赛者的 信息和成绩,包括其所代表的学校的编号(从1 开始连续编号)及其比赛成绩(百分制)…...
-查询优化(23)-避免全表扫描)
【MySQL精通之路】SQL优化(1)-查询优化(23)-避免全表扫描
当MySQL使用全表扫描来解析查询时,EXPLAIN的输出在type列中显示ALL。 这种情况通常发生在以下情况下: 该表非常小,因此执行全表扫描比查找关键字更快。这对于少于10行且行长较短的表来说很常见。 对于索引列,ON或WHERE子句中没有…...
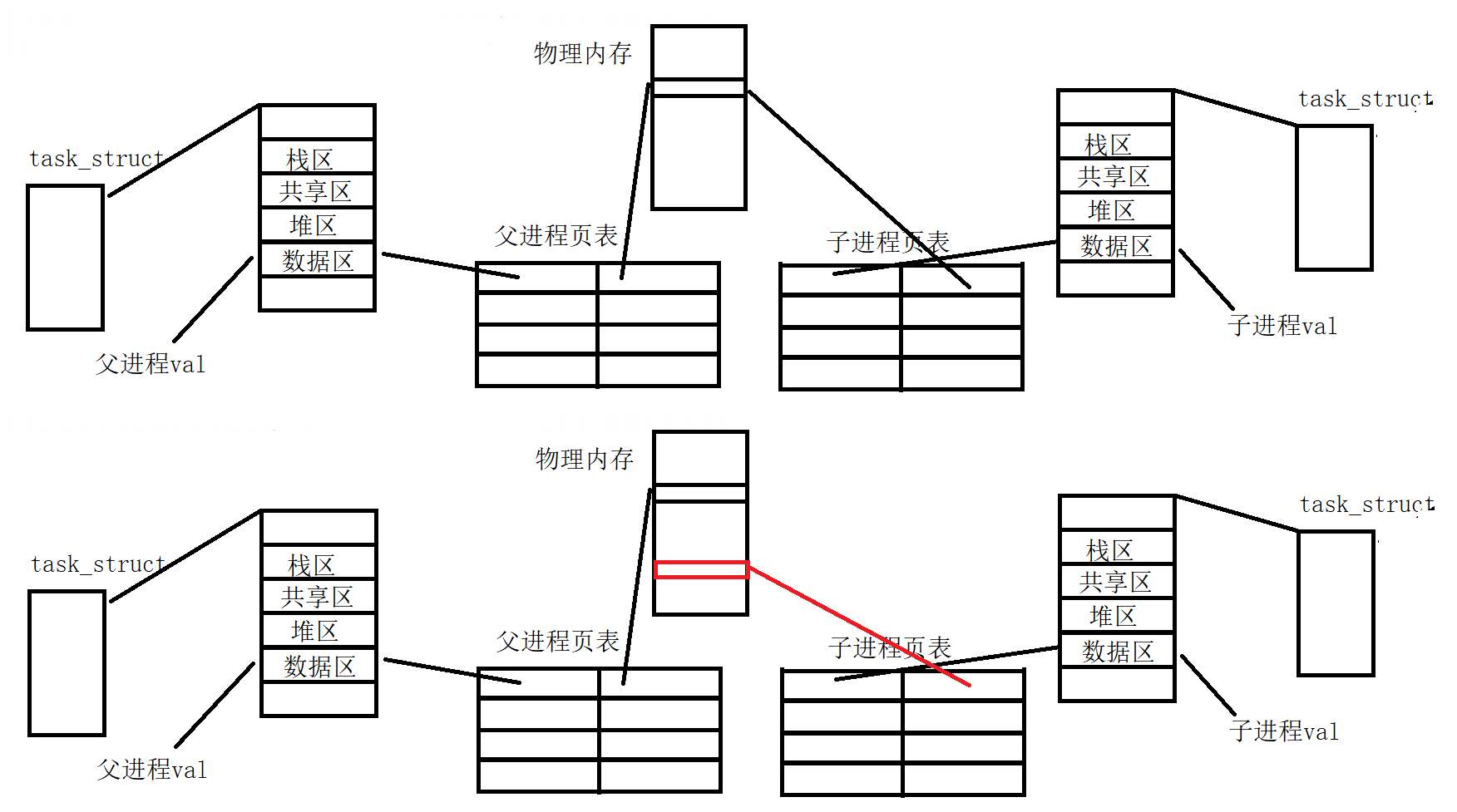
【Linux】写时拷贝技术COW (copy-on-write)
文章目录 Linux写时拷贝技术(copy-on-write)进程的概念进程的定义进程和程序的区别PCB的内部构成 程序是如何被加载变成进程的?写时复制(Copy-On-Write, COW)写时复制机制的原理写时拷贝的场景 fork与COWvfork与fork Linux写时拷贝技术(copy-…...

用python使用主成分分析数据
import pandas as pd #导入处理二维表格的库 import numpy as np #导入数值计算的库 from sklearn.preprocessing import StandardScaler #导入数据标准化模块 import matplotlib.pyplot as plt #导入画图的包 from sklearn.decomposition import PCA #导入主成…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
