【Python特征工程系列】一文教你使用PCA进行特征分析与降维(案例+源码)
这是我的第287篇原创文章。
一、引言
主成分分析(Principal Component Analysis, PCA)是一种常用的降维技术,它通过线性变换将原始特征转换为一组线性不相关的新特征,称为主成分,以便更好地表达数据的方差。
在特征重要性分析中,PCA 可以用于理解数据中最能解释方差的特征,并帮助识别对目标变量影响最大的特征。可以通过查看PCA的主成分(主特征向量)以及各主成分所对应的特征重要性来推断哪些原始特征在新特征中起到了较大影响。
PCA 的局限性:
- PCA 是一种线性变换方法,可能无法很好地处理非线性关系的数据。
- PCA 可能会丢失一些信息,因为它主要关注的是数据中的方差,而忽略了其他方面的信
- PCA 假设主成分与原始特征之间是线性关系,这在某些情况下可能不成立。
二、实现过程
2.1 读取数据
# 准备数据
data = pd.read_csv(r'dataset.csv')
df = pd.DataFrame(data)
print(df)
# 目标变量和特征变量
target = 'target'
features = df.columns.drop(target)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(df[features], df[target], test_size=0.2, random_state=0)df:

2.2 对训练集做PCA主成分分析
自主选择主成分,并打印出每个主成分的解释性方差:
pca = PCA(n_components='mle')
pca.fit(X_train)
var_ratio = pca.explained_variance_ratio_
for idx, val in enumerate(var_ratio, 1):print("Principle component %d: %.2f%%" % (idx, val * 100))
print("total: %.2f%%" % np.sum(var_ratio * 100))结果:
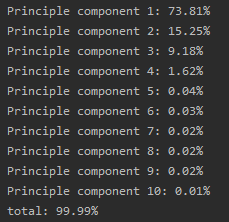
共计10个主成分。
2.3 通过主成分分析原始特征重要性
打印出每个特征对于主成分的系数,这反映了原始特征的重要性:
print(pca.components_)结果:
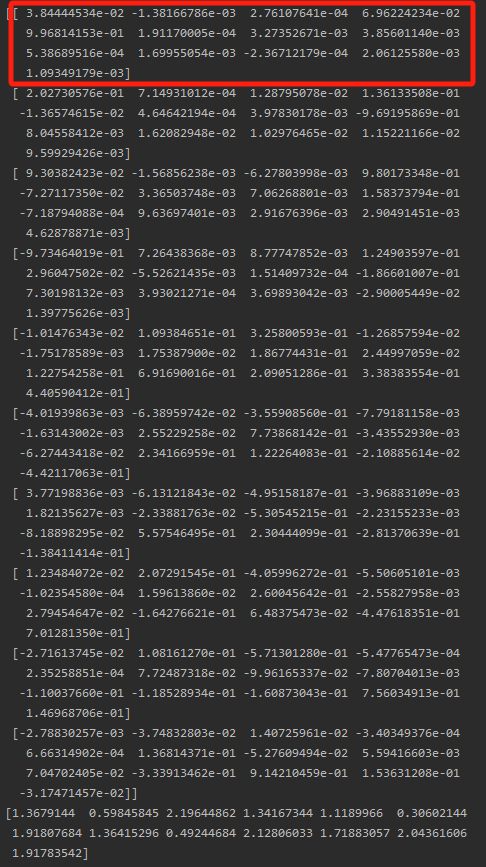
通过计算10个主成分中,每个原始特征的系数绝对值之和作为该特征的最终贡献度:
# 计算原始特征与主成分的相关性(绝对值)
feature_importance = np.abs(pca.components_)
# 计算每个主成分中原始特征的权重(系数)和
feature_importance_sum = np.sum(feature_importance, axis=0)
# 打印原始特征的重要性(贡献度)
print("\n原始特征的重要性(贡献度):")
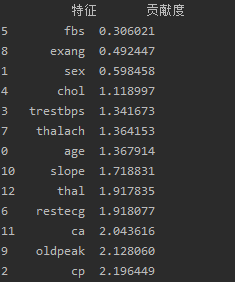
ranking_df = pd.DataFrame({'特征': features, '贡献度': feature_importance_sum})
ranking_df = ranking_df.sort_values(by='贡献度')
print(ranking_df)结果:
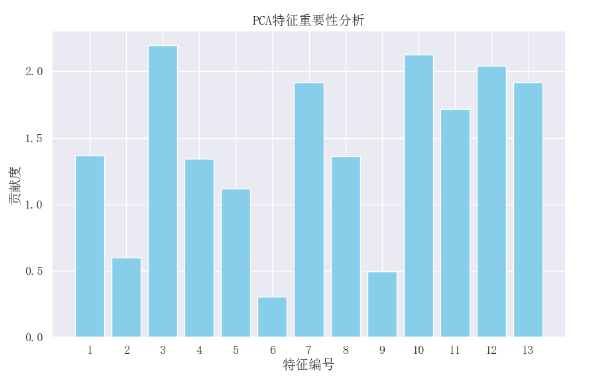
可视化:
2.4 查看累计解释方差比率与主成分个数的关系
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.arange(1, len(var_ratio) + 1), np.cumsum(var_ratio), "-ro")
ax.set_title("Cumulative Explained Variance Ratio", fontsize=15)
ax.set_xlabel("number of components")
ax.set_ylabel("explained variance ratio(%)")
plt.show()结果:
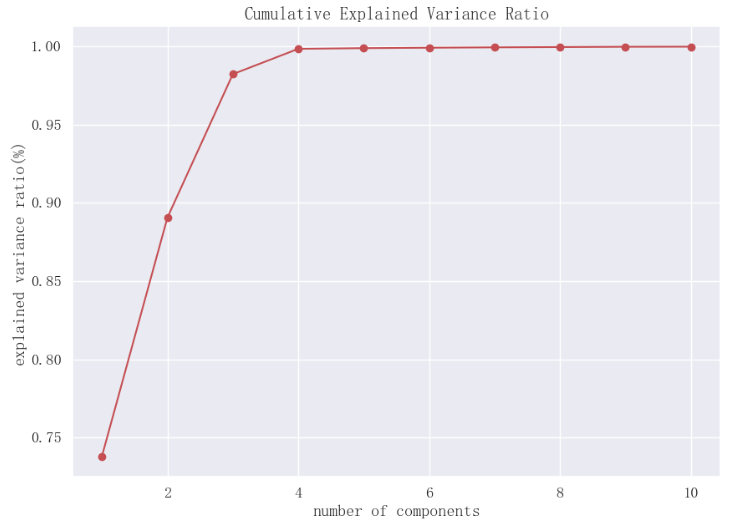
前2个主成分累计解释性方差比率接近0.9,前3个主成分累计解释方差比率超过0.95。
2.5 自动选择最优的主成分个数
设定累计解释方差比率的目标,让sklearn自动选择最优的主成分个数:
target = 0.9 # 保留原始数据集90%的变异
res = PCA(n_components=target).fit_transform(X_train)
print("original shape: ", X_train.shape)
print("transformed shape: ", res.shape)结果:
![]()
选择了3个主成分。
2.6 主成分选择可视化(以2个主成分为例)
选择两个主成分,并进行可视化:
pca=PCA(n_components=2) #加载PCA算法,设置降维后主成分数目为2
reduced_x=pca.fit_transform(X_train)#对样本进行降维
principalDf = pd.DataFrame(data = reduced_x, columns = ['principal component 1', 'principal component 2'])
print(principalDf)
y_train = np.array(y_train)
yes_x,yes_y=[],[]
no_x,no_y=[],[]
for i in range(len(reduced_x)):if y_train[i] ==1:yes_x.append(reduced_x[i][0])yes_y.append(reduced_x[i][1])elif y_train[i]==0:no_x.append(reduced_x[i][0])no_y.append(reduced_x[i][1])
plt.scatter(yes_x,yes_y,c='r',marker='x')
plt.scatter(no_x,no_y,c='b',marker='D')
plt.xlabel("First Main Component")
plt.ylabel("Second Main Component")
plt.show()结果:
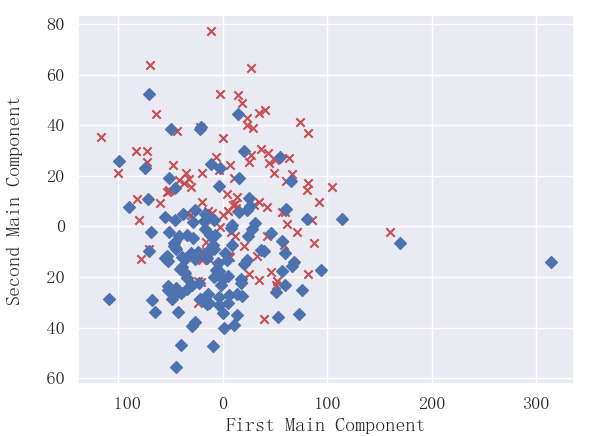
可以看出2个主成分可以大概划分出两类。
作者简介:
读研期间发表6篇SCI数据挖掘相关论文,现在某研究院从事数据算法相关科研工作,结合自身科研实践经历不定期分享关于Python、机器学习、深度学习、人工智能系列基础知识与应用案例。致力于只做原创,以最简单的方式理解和学习,关注我一起交流成长。需要数据集和源码的小伙伴可以关注底部公众号添加作者微信。
相关文章:

【Python特征工程系列】一文教你使用PCA进行特征分析与降维(案例+源码)
这是我的第287篇原创文章。 一、引言 主成分分析(Principal Component Analysis, PCA)是一种常用的降维技术,它通过线性变换将原始特征转换为一组线性不相关的新特征,称为主成分,以便更好地表达数据的方差。 在特征重要…...

【Linux】Ubuntu系统挂载NAS文件夹
测试系统:Ubuntu24.02 1. 安装必要的软件包 sudo apt update sudo apt install cifs-utils 2. 创建挂载点 sudo mkdir -p /mnt/nas 3. 获取当前用户的 UID 和 GID id -u id -g 4. 挂载:设置用户名/密码/nas地址 sudo mount -t cifs -o username,…...
如何用ai打一场酣畅淋漓的数学建模比赛? 给考研加加分!
文章目录 数学建模比赛1. 数学建模是什么?2. 数学建模分工合作2.1 第一:组队和分工合作2.2 第二:充分的准备2.3 第三:比赛中写论文过程 3. 数学建模基本过程4. 2023全年数学建模竞赛时间轴5. 数学建模-资料大全6. 数学建模实战 数…...
深入浅出MySQL事务实现底层原理
重要概念 事务的ACID 原子性(Atomicity):即不可分割性,事务中的操作要么全不做,要么全做一致性(Consistency):一个事务在执行前后,数据库都必须处于正确的状态…...
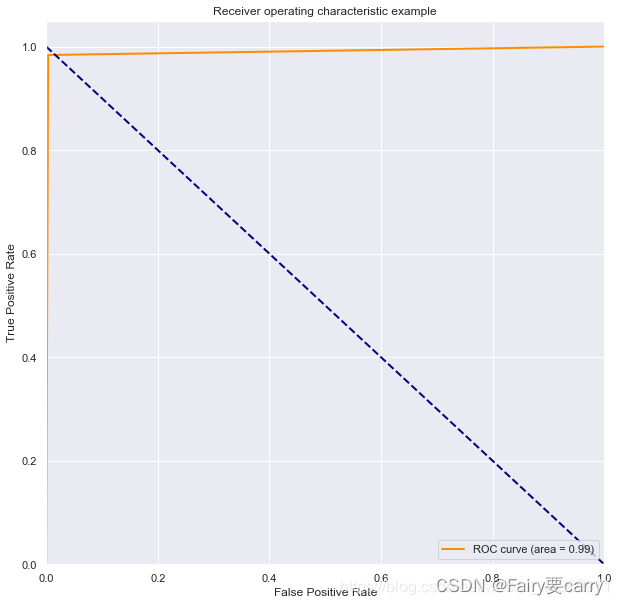
SVM兵王问题
1.流程 前面六个就是棋子的位置,draw就是逼和,后面的数字six就代表,白棋最少用六步就能将死对方。然后呢,可以看一下最后一个有几种情况: 2.交叉测试 leave one out: 留一个样本作测试集,其余…...

yolov5_obb
yolov5_obb: 旋转目标检测从数据制作到终端部署全流程教学...
NextJs 初级篇 - 安装 | 路由 | 中间件
NextJs 初级篇 - 安装 | 路由 | 中间件 一. NextJs 的安装二. 路由2.1 路由和页面的定义2.2 布局的定义和使用2.3 模板的定义和使用① 模板 VS 布局② 什么是 use client 2.4 路由跳转的方式2.5 动态路由2.6 路由处理程序① GET 请求的默认缓存机制② 控制缓存或者退出缓存的手…...

变分自动编码器(VAE)深入理解与总结
本文导航 0 引言1 起源1.1 自编码器的任务定义1.2 自编码器存在的问题1.3 VAE的核心思路 2 VAE的建模过程2.1 VAE的任务定义2.2 真实分布 ϕ \phi ϕ是什么,为什么要逼近这个分布的参数,如何做?2.3 “重参数化(Reparameterization…...

Leetcode 剑指 Offer II 079.子集
题目难度: 中等 原题链接 今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复 剑指offer2 就能看到该系列当前连载的所有文章了, 记得关注哦~ 题目描述 给定一个整数数组 nums ,数组中的元素 互不相同 。返…...

Linux基础命令常见问题解决方案
Linux 基础命令常见问题解决方案 在Linux的日常使用中,用户经常会遇到各种各样的问题。本文旨在提供一个关于Linux基础命令的常见问题及其解决方案的全面指南。我们将覆盖30种不同的错误场景,并给出具体的解决步骤和示例,帮助初学者快速定位…...
 ——使用LINQ进行匿名对象初始化)
LINQ(五) ——使用LINQ进行匿名对象初始化
总目录 C# 语法总目录 上一篇:LINQ(四) ——使用LINQ进行对象类型初始化 LINQ 五 ——使用LINQ进行匿名对象初始化 6.2 匿名类型 6.2 匿名类型 可以不用声明定义一个对象,直接使用new,然后直接赋值即可 string[] names { "Tom",…...
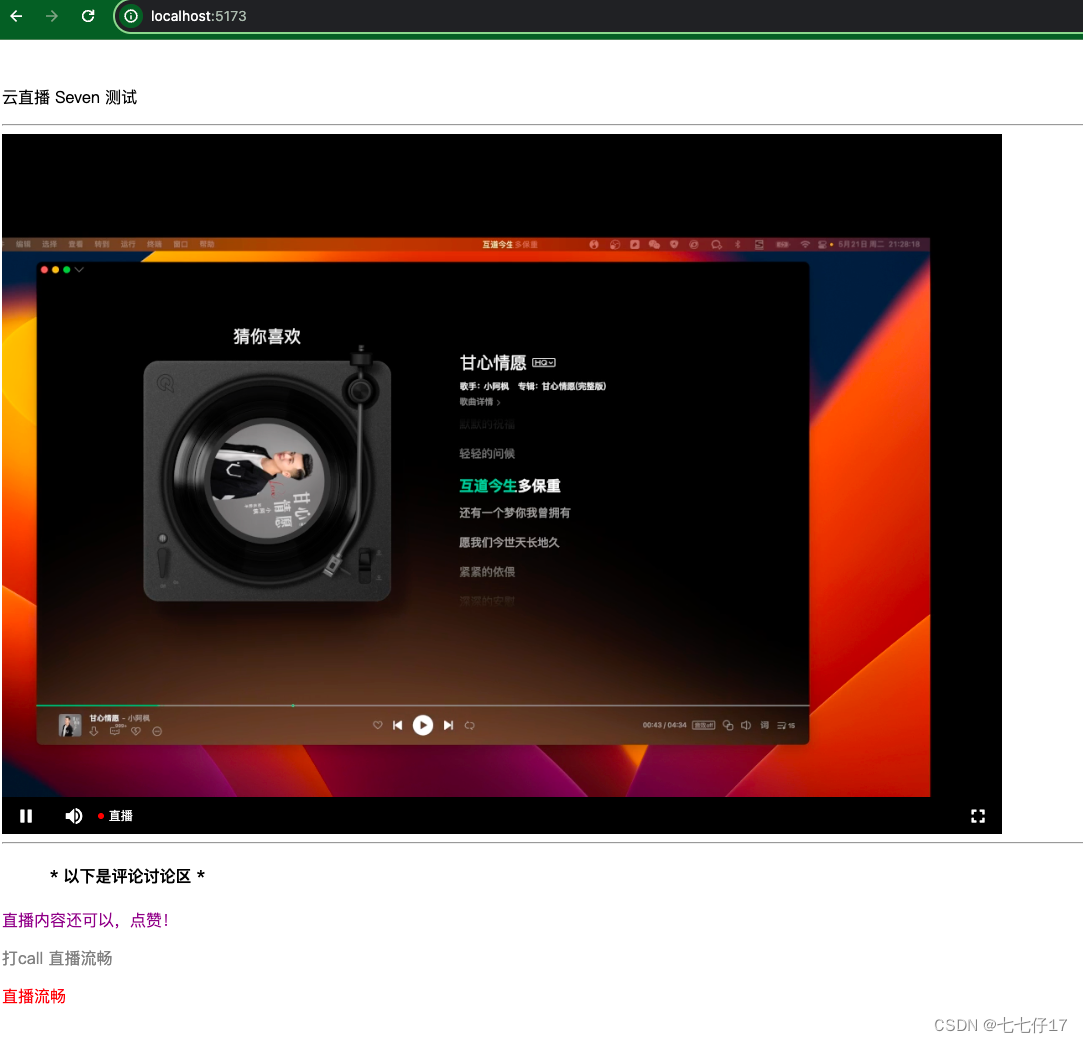
1小时从0开始搭建自己的直播平台(详细步骤)
本文讲述了如何从0开始,利用腾讯云的平台,快速搭建一个直播平台的过程。 文章目录 效果图详细步骤准备工作第一步:添加域名并检验cname配置1.先填加一个推流域名2. 点击完下一步,得到一个cname地址3. 将cname地址,配置…...

Python打包篇-exe
文章目录 pyinstallerauto-py-to-exe pyinstaller 命令行工具,语法自行查看官方help pip install pyinstallerauto-py-to-exe 基于pyinstaller的一款GUI工具,会自行打包py文件中依赖的库 pip install auto-py-to-exe auto-py-to-exe.exe //运行即可...

游戏找不到d3dcompiler_43.dll怎么办,教你5种可靠的修复方法
在电脑使用过程中,我们经常会遇到一些错误提示,其中之一就是“找不到d3dcompiler43.dll”。这个问题通常出现在游戏或者图形处理软件中,它会导致程序无法正常运行。为了解决这个问题,我经过多次尝试和总结,找到了以下五…...

如何使用多种算法解决LeetCode第135题——分发糖果问题
❤️❤️❤️ 欢迎来到我的博客。希望您能在这里找到既有价值又有趣的内容,和我一起探索、学习和成长。欢迎评论区畅所欲言、享受知识的乐趣! 推荐:数据分析螺丝钉的首页 格物致知 终身学习 期待您的关注 导航: LeetCode解锁100…...
泰拉瑞亚从零开始的开服教程
前言 本教程将讲诉使用Linux系统搭建泰拉瑞亚服务器(因为网上已经有很完善的windows开服教程了),使用的Linux发行版是Debian11,服务端使用的程序是TShock,游戏版本是1.4.4.9 所需要准备的 一台服务器(本教程使用的是…...
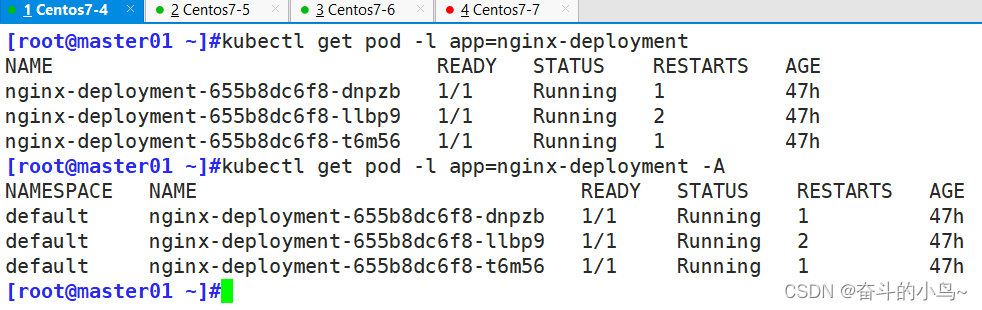
【云原生】K8s管理工具--Kubectl详解(一)
一、陈述式管理 1.1、陈述式资源管理方法 kubernetes 集群管理集群资源的唯一入口是通过相应的方法调用 apiserver 的接口kubectl 是官方的 CLI 命令行工具,用于与 apiserver 进行通信,将用户在命令行输入的命令,组织并转化为apiserver 能识…...

2024.5.26.python.exercise
# # 导入包 # from pyecharts.charts import Bar, Timeline # from pyecharts.options import LabelOpts, TitleOpts # from pyecharts.globals import ThemeType # # # 从文件中读取信息 # GDP_file open("1960-2019全球GDP数据.csv", "r", encoding&quo…...
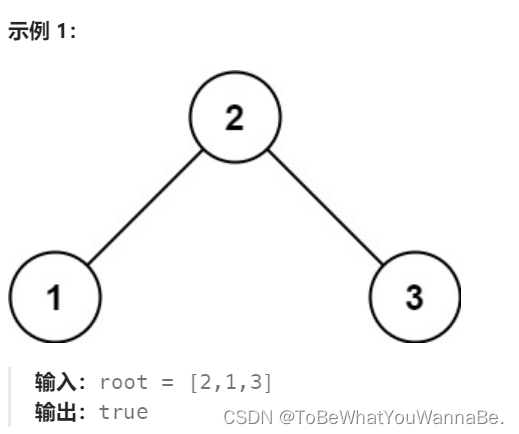
代码随想录-Day20
654. 最大二叉树 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大值 右边 的 子数组后缀上 构建右子树。 返回 nums…...

揭秘C++ String容器:字符串操作的艺术
目录 编辑 引言 一、初识std::string:构造与初始化 二、字符串的操纵艺术:拼接、查找与替换 三、访问与遍历:字符的细腻触感 四、大小与容量:动态调整的智慧 五、进阶功能:探索更多可能 结语 引言 在C标准库…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
