Unity算法(一)——快速排序算法
文章目录
- 前言
- 快速排序算法
- 1、概念与实现
- 2、优化
前言
算法是程序员的基础能力之一,资质越老的程序员在这方面理解会越深,很多时候项目在某个需要优化、提升的节点时,往往一些算法的使用就可以大大提升程序性能。当然,对于不同项目需求,要用适合的算法,在效率与业务之间寻找平衡。
此为第一章,快排算法。
快速排序算法
1、概念与实现
平均时间复杂度为O(n log n),最坏的情况是O(n ^ 2)。但综合的看比许多其他简单的排序算法(如插入排序和选择排序)的O(n²)更高效,所以使用面也更广。
排序分为几步:
1、选取一个基准元素
2、把比她小的移到左侧,大的移到右侧
3、对两侧的元素进行递归筛选,然后再对两侧的元素执行第一步操作
我们从中能分析出最坏的结果就是每次都选择最小的元素和最大的元素,示例代码我就使用AI生成了,毕竟网上一搜就有。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
/*
代码分析:
QuickSort方法:
递归地对数组进行排序。首先通过Partition方法将数组划分,然后对划分后的子数组进行排序。Partition方法:
选择数组的最后一个元素作为枢轴(pivot)。
将所有小于枢轴的元素移动到枢轴的左边,大于枢轴的元素移动到右边。
返回枢轴的位置。Swap方法:
交换数组中两个元素的位置。ArrayToString方法:
将数组转换为字符串格式,以便在控制台中打印。
*/
public class QuickSortExample : MonoBehaviour
{void Start(){int[] array = { 34, 7, 23, 32, 5, 62 };Debug.Log("Unsorted Array: " + ArrayToString(array));QuickSort(array, 0, array.Length - 1);Debug.Log("Sorted Array: " + ArrayToString(array));}void QuickSort(int[] array, int low, int high){if (low < high){int pi = Partition(array, low, high);QuickSort(array, low, pi - 1);QuickSort(array, pi + 1, high);}}int Partition(int[] array, int low, int high){int pivot = array[high];int i = (low - 1);for (int j = low; j < high; j++){if (array[j] < pivot){i++;Swap(ref array[i], ref array[j]);}}Swap(ref array[i + 1], ref array[high]);return (i + 1);}void Swap(ref int a, ref int b){int temp = a;a = b;b = temp;}string ArrayToString(int[] array){return string.Join(", ", array);}
}2、优化
(1)随机选取中轴数
在快速排序算法中,选取哪个元素作为枢轴(pivot)是至关重要的,因为这会直接影响到算法的排序效率。如果选取的枢轴不是数组中间位置的数字,而是偏向于较小或较大的数字,排序速度就会受到影响。如果选取的枢轴恰好是最大或最小的数字,情况将更糟,因为这样会导致左侧或右侧没有元素可排序,相当于每次遍历只完成了一个元素的排序。由于确定确切的中位数需要耗费大量的计算资源,因此我们只能通过随机选择元素来降低出现最坏情况的概率。虽然随机选择旨在减少选取最大值和最小值的概率,但实际上,随机选择可能会选取到不理想的枢轴元素。因此,尽管随机选择能够一定程度上降低最坏情况的发生概率,但对于排序来说,随机选择并没有提供太大的帮助。
通过随机选择枢轴,可以减少最坏情况发生的概率:
void QuickSort(int[] array, int low, int high)
{if (low < high){int pi = RandomizedPartition(array, low, high);QuickSort(array, low, pi - 1);QuickSort(array, pi + 1, high);}
}int RandomizedPartition(int[] array, int low, int high)
{int pivotIndex = Random.Range(low, high + 1);Swap(ref array[pivotIndex], ref array[high]);return Partition(array, low, high);
}(2)三向切分
既然知道原理,我们其实也能猜到,如果中轴数更接近中位数,效率会大幅提升。为了确保选择的中轴数更接近于中位数,可以采取一种策略:在排序之前,首先对数组的头部、中部和尾部的三个元素进行排序,将最小的数字放在头部,中间的数字放在中部,最大的数字放在尾部。然后用3个数字去提高有效接近中位数的中轴元素。
三向切分将数组分为三部分:小于枢轴的部分、等于枢轴的部分和大于枢轴的部分,适用于大量重复元素的情况:
void QuickSort3Way(int[] array, int low, int high)
{if (low < high){int lt = low, i = low + 1, gt = high;int pivot = array[low];while (i <= gt){if (array[i] < pivot)Swap(ref array[lt++], ref array[i++]);else if (array[i] > pivot)Swap(ref array[i], ref array[gt--]);elsei++;}QuickSort3Way(array, low, lt - 1);QuickSort3Way(array, gt + 1, high);}
}(3)小区间使用插入排序
排序算法有各自的使用量级,当量级不同时,排序效率可能不一样。以插入排序为例,它对列表的有序程度和元素数量都十分敏感。当列表几乎有序时,插入排序表现最佳,因为它只需要简单地比较少量元素并执行少量交换操作。相反,如果列表几乎是逆序的,插入排序的性能将急剧下降,因为它需要大量的比较和交换操作来将每个元素移动到正确的位置。
在小数组(如小于10个元素)时,插入排序比快速排序更高效。可以设置一个阈值,当子数组小于该阈值时,使用插入排序:
void QuickSort(int[] array, int low, int high)
{const int CUTOFF = 10;if (high <= low + CUTOFF - 1){InsertionSort(array, low, high);return;}if (low < high){int pi = RandomizedPartition(array, low, high);QuickSort(array, low, pi - 1);QuickSort(array, pi + 1, high);}
}void InsertionSort(int[] array, int low, int high)
{for (int i = low; i <= high; i++){for (int j = i; j > low && array[j] < array[j - 1]; j--){Swap(ref array[j], ref array[j - 1]);}}
}相关文章:
——快速排序算法)
Unity算法(一)——快速排序算法
文章目录 前言快速排序算法1、概念与实现2、优化 前言 算法是程序员的基础能力之一,资质越老的程序员在这方面理解会越深,很多时候项目在某个需要优化、提升的节点时,往往一些算法的使用就可以大大提升程序性能。当然,对于不同项…...

Leetcode 2028
思路:1-6之间的的n个数组合起来要变成sum_t mean*(rolls.size()n) - sum(rolls) ; 那么可以先假设每个数都是sum_t / n 其中这个数必须要在1 - 6 之间否者无法分配。 然后可以得出n * (sum_t / n ) < sum ; 需要对余数mod进行调整,为了减少调整的次…...
Angular(1):使用Angular CLI创建空项目
要创建一个空的 Angular 项目,可以使用 Angular CLI(命令行界面)。以下是使用 Angular CLI 创建一个新项目的步骤: 1、安装 Angular CLI: 打开你的命令行界面(在 Windows 上是 CMD、PowerShell 或 Git Bas…...
算法原题)
字节跳动(校招)算法原题
大模型"价格战"越演越烈 昨天的 文章 提到,自从 5 月 15 号,字节跳动发布了击穿行业底价的豆包大模型后,各大厂家纷纷跟进降价,而且都不是普通降价,要么降价 90% 以上,要么直接免费。 今天是豆包…...

前端面试题日常练-day39 【面试题】
题目 希望这些选择题能够帮助您进行前端面试的准备,答案在文末。 1. 哪个jQuery方法用于设置元素的HTML内容? a) .html() b) .text() c) .val() d) .append() 2. 在jQuery中,以下哪个方法用于隐藏或显示一个元素? a) .toggle…...
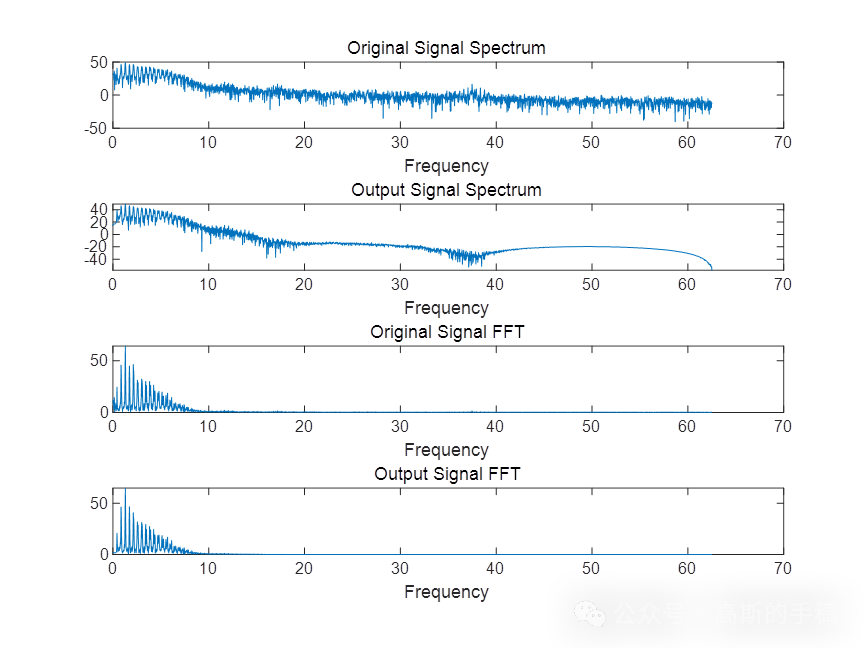
心电信号降噪方法(滤波器/移动平均/小波等,MATLAB环境)
对于一个正常的、完整的心动周期,对应的心电图波形如下图所示,各个波形都对应着心脏兴奋活动的生理过程,包含P波,PR段,QRS波群,ST段,T波,U波。 (1)P波心电图中…...

Kubernetes 文档 / 概念 / 工作负载 / 管理工作负载
Kubernetes 文档 / 概念 / 工作负载 / 管理工作负载 此文档从 Kubernetes 官网摘录 中文地址 英文地址 你已经部署了你的应用并且通过 Service 将其暴露出来。现在要做什么? Kubernetes 提供了一系列的工具帮助你管理应用的部署,包括扩缩和更新。 组织…...

【第6章】SpringBoot整合Mybatis
文章目录 前言一、准备1. 版本要求2.安装3. 建表语句 二、案例1. mapper2.实体类3.测试类4.扫描5. 配置6. mapper.xml7.输出 总结 前言 MyBatis-Spring-Boot-Starter 可以帮助你更快地在 Spring Boot 之上构建 MyBatis 应用。 一、准备 1. 版本要求 MyBatis-Spring-Boot-Sta…...

vim常用指令——001
vim常用指令 Vim的命令模式常用操作一、定位移动光标二、行的基本操作【复制、粘贴、删除】三、查找、替换四、分屏命令 总结给大家总结下四个运行模式: Vim的命令模式常用操作 一、定位移动光标 按h:将光标向左移动一个字符,等同于方向键左…...
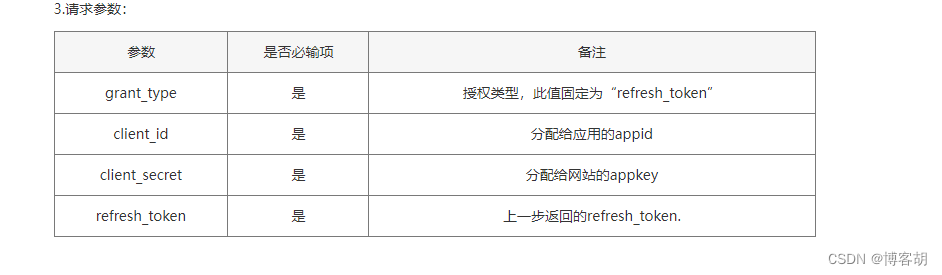
java 对接农行支付相关业务(二)
文章目录 农行掌银集成第三方APP1:掌银支付对接快e通的流程1.1 在农行网站上注册我们的app信息([网址](https://openbank.abchina.com/Portal/index/index.html))1.2:java整合农行的jar包依赖1.3:把相关配置信息整合到项目中1.4:前端获取授权码信息1.5:后端根据授权码信…...
超频是什么意思?超频的好处和坏处
你是否曾经听说过超频?在电脑爱好者的圈子里,这个词似乎非常熟悉,但对很多普通用户来说,它可能还是一个神秘而陌生的存在。 电脑超频是什么意思 电脑超频(Overclocking),顾名思义,是…...

【cocos creator】进度条控制脚本,支持节点进度条,图片进度条,进度条组件,和进度文字展示
进度条控制脚本,支持节点进度条,图片进度条,进度条组件,和进度文字展示 const { ccclass, property, menu } cc._decorator;let text_type cc.Enum({"20%": 0,"1/5": 1,"差值": 2,"自定义…...

Bean的一些属性信息总结
我们知道,在Spring中,一个Bean可以理解为一个对象,但是二者之间肯定是有区别的,比如一个Bean可以实例化成很多个对象、Bean中可以带有某些描述信息。 学习Bean,能更好地使用Bean。 1、Spring两个核心概念的由来【可忽…...

CentOS 7 安装 Minio
获取MinIO安装包 下载地址如下:下载地址通过以下命令可直接将安装包下载至服务器 wget https://dl.min.io/server/minio/release/linux-amd64/archive/minio-20230809233022.0.0.x86_64.rpm安装MinIO rpm -ivh minio-20230809233022.0.0.x86_64.rpm集成Systemd …...
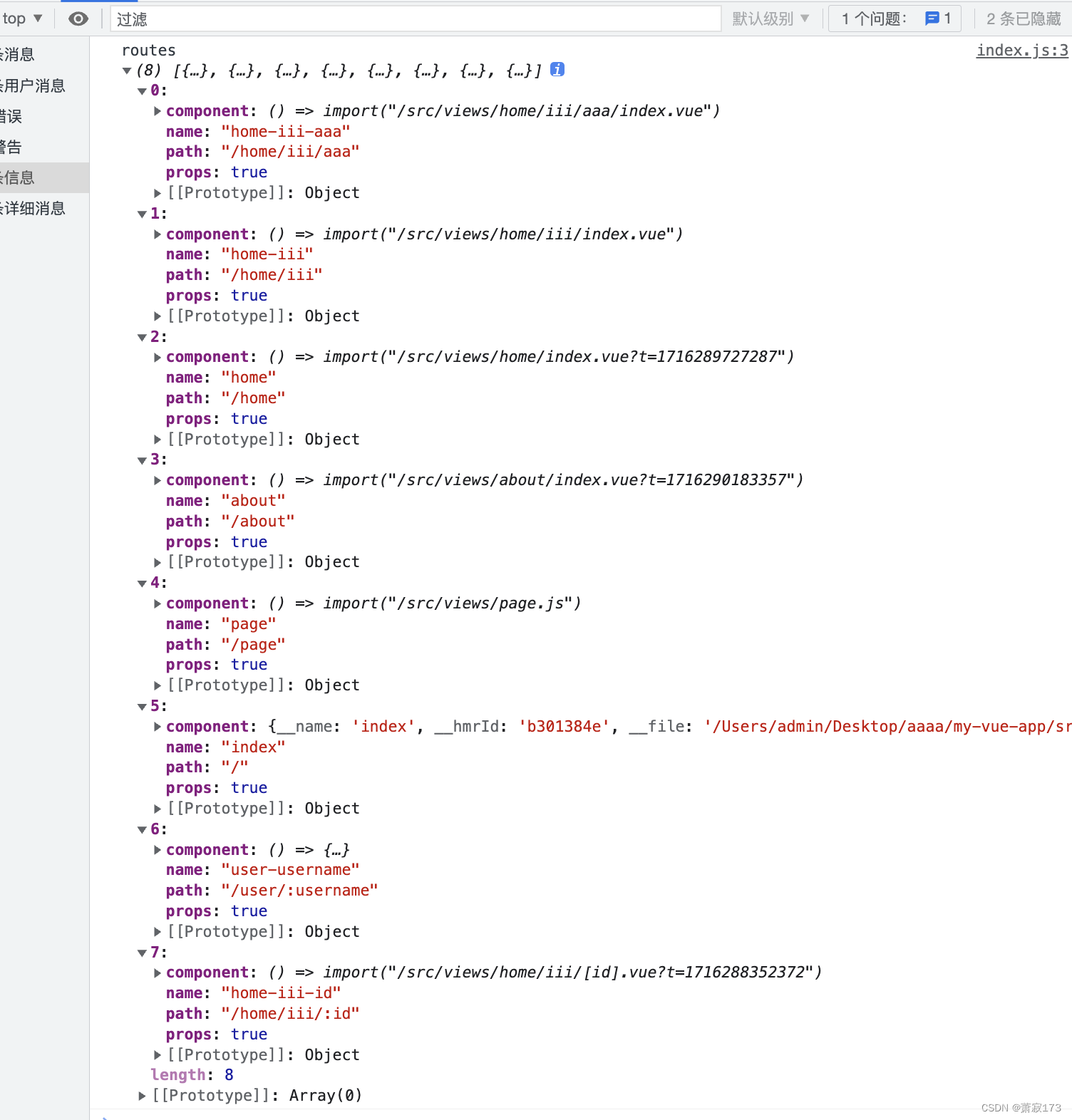
vue3和vite实现vue-router4版本路由的配置以及自动生成路由配置
这个是普通的手动路由配置:https://blog.csdn.net/weixin_68658847/article/details/130071101 自动路由配置 创建项目 npm create vitelatest my-vue-app -- --template vue // 或者 yarn create vite my-vue-app --template vue// 安装路由 yarn add vue-route…...

Flutter 中的 CupertinoDatePicker 小部件:全面指南
Flutter 中的 CupertinoDatePicker 小部件:全面指南 在 Flutter 中,CupertinoDatePicker 是 Cupertino 组件库的一部分,它提供了一个 iOS 风格的日期选择器。这个选择器允许用户选择日期和时间,非常适合需要符合 iOS 设计指南的应…...

用 Python 编写自动发送每日电子邮件报告的脚本
第一步:安装必要的库 你需要安装 smtplib(Python 自带),但你需要安装 schedule 和 email 库。你可以使用以下命令安装这些库: pip install schedule第二步:编写发送邮件的脚本 这里是一个完整的 Python …...

IT人的拖延——渴望成功与害怕成功的矛盾
很多人都以为,害怕失败是拖延的主要诱因,但其实“害怕成功”也是拖延的主要诱因之一。要说这个原因,我们不得不提起Bible中的一个人“约拿”,让我们先来看看他的故事带给我们什么启示。 约拿情结简介 约拿是Bible中的一名先知&a…...

【全开源】场馆预定系统源码(ThinkPHP+FastAdmin+UniApp)
一款基于ThinkPHPFastAdminUniApp开发的多场馆场地预定小程序,提供运动场馆运营解决方案,适用于体育馆、羽毛球馆、兵乒球馆、篮球馆、网球馆等场馆。 场馆预定系统源码:打造高效便捷的预定体验 一、引言:数字化预定时代的来临 …...
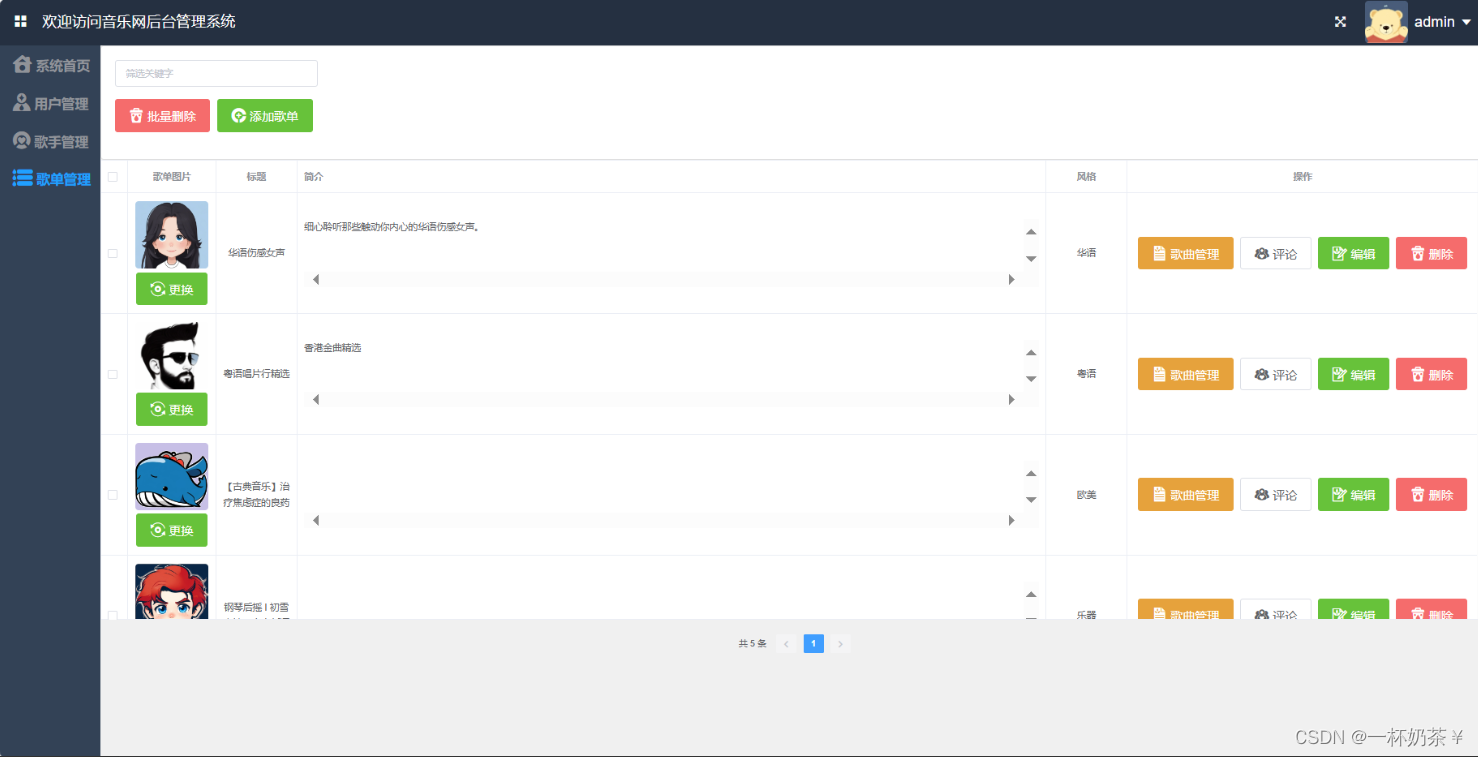
音乐系统java在线音乐网站基于springboot+vue的音乐系统带万字文档
文章目录 音乐系统一、项目演示二、项目介绍三、万字项目文档四、部分功能截图五、部分代码展示六、底部获取项目源码和万字论文参考(9.9¥带走) 音乐系统 一、项目演示 在线音乐系统 二、项目介绍 基于springbootvue的前后端分离在线音乐系…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...
