docker image分析利器之dive
dive是一个用于研究 Docker 镜像、层内容以及发现缩小 Docker/OCI 镜像大小方法的开源工具.
开源地址: dive github
为了有个直观的印象, 可以先看一下repo文档中的gif图:

安装
在Ubuntu/Debian系统下,可以使用deb包安装:
DIVE_VERSION=$(curl -sL "https://api.github.com/repos/wagoodman/dive/releases/latest" | grep '"tag_name":' | sed -E 's/.*"v([^"]+)".*/\1/')
curl -OL https://github.com/wagoodman/dive/releases/download/v${DIVE_VERSION}/dive_${DIVE_VERSION}_linux_amd64.deb
sudo apt install ./dive_${DIVE_VERSION}_linux_amd64.deb
可能会遇到下载的问题,可以在repo的release中,找到适合当前os及arch的安装包,然后执行 sudo apt install.
其他系统的安装请参照仓库文档.
docker image方式
dive提供了docker镜像, 如果不想安装在本地,可以用docker的方式运行.
首先下载镜像:
docker pull wagoodman/dive
或者自行build,从官方repo clone代码到本地后,执行build命令:
docker build -t "your-image-tag" .
然后执行:
docker run -it --rm -v /var/run/docker.sock:/var/run/docker.sock wagoodman/dive <your-docker-image-tag>
注意这里的-v /var/run/docker.sock:/var/run/docker.sock是必须的.
或者为了方便,也可以创建一个alias:
alias dive="docker run -ti --rm -v /var/run/docker.sock:/var/run/docker.sock wagoodman/dive"
运行镜像分析
我们用如下命令来分析一个镜像:
dive nginx:latest
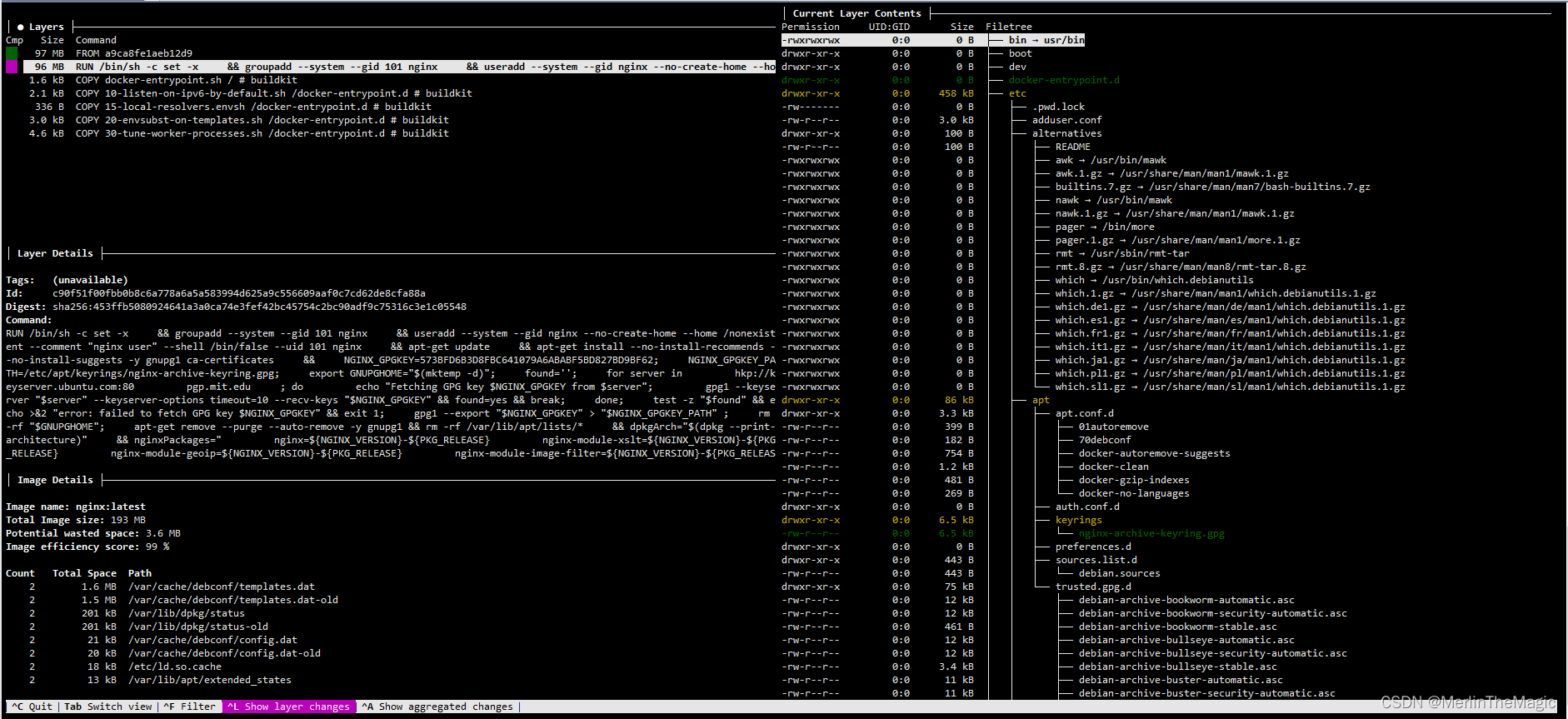
可以得到如上图所示的输出.通过上下健移动,可以看到不同layer的信息,包括执行的command, 当前layer的文件系统信息, 文件的变化等…
官方文档中给出的功能列表包括:
显示 Docker 镜像分层内容
当您在左侧选择一个层时,您将在右侧看到该层及其之前所有层的内容。您还可以使用箭头键完全浏览文件树。
指示每个层中的变更
文件树中会标出哪些文件发生了变更、修改、添加或删除。这可以调整为显示特定层的变更,或累积到该层的变更。
估算"镜像效率"
左下窗格显示基本层信息和一个实验性指标,用于猜测您的镜像中包含多少浪费的空间。这可能是由于在层之间重复文件、移动文件或未完全删除文件造成的。它提供了百分比"得分"和总的浪费文件空间。
小结
dive是一个非常有用的小工具,可以帮助我们很直观的分析镜像,尤其是可以看到镜像中文件系统的变化; 另外镜像效率这个功能也很有用, 可以用于image的大小优化. 在打包一些LLM模型镜像时,由于大量的python三方包和推理加速中间件的安装,很容易造成镜像变得巨大无比,对镜像尺寸压缩优化就变得重要起来. 后续会继续分享如何优化docker image的大小,欢迎交流.
相关文章:

docker image分析利器之dive
dive是一个用于研究 Docker 镜像、层内容以及发现缩小 Docker/OCI 镜像大小方法的开源工具. 开源地址: dive github 为了有个直观的印象, 可以先看一下repo文档中的gif图: 安装 在Ubuntu/Debian系统下,可以使用deb包安装: DIVE_VERSION$(curl -sL "https:/…...

java组合设计模式Composite Pattern
组合设计模式(Composite Pattern)是一种结构型设计模式,它允许你将对象组合成树形结构来表示“部分-整体”的层次结构。组合模式使得客户端对单个对象和组合对象的使用具有一致性。 // Component - 图形接口 interface Graphic {void draw()…...
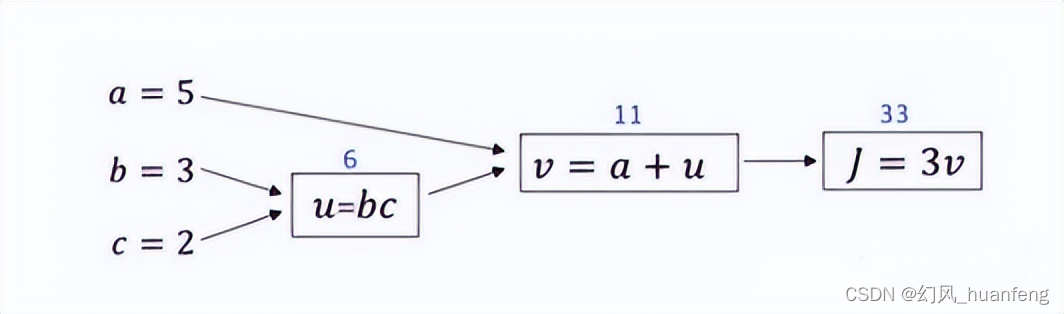
每天五分钟深度学习:如何使用计算图来反向计算参数的导数?
本文重点 在上一个课程中,我们使用一个例子来计算函数J,也就相当于前向传播的过程,本节课程我们将学习如何使用计算图计算函数J的导数。相当于反向传播的过程。 计算J对v的导数,dJ/dv3 计算J对a的导数,dJ/da…...
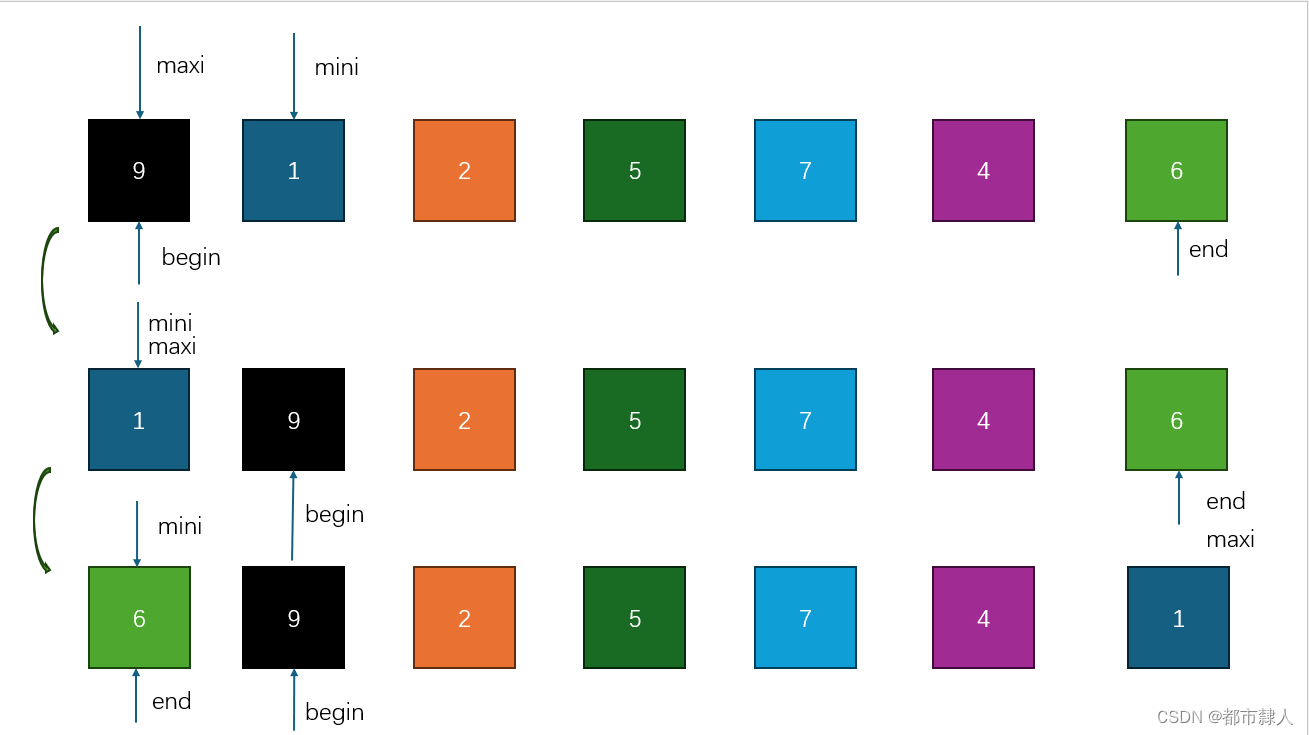
常见排序算法之选择排序
目录 一、选择排序 1.1 什么是选择排序? 1.2 思路 1.2.1 思路一 1.2.2 优化思路 1.3 C语言源码 1.3.1 思路一 1.3.2 优化思路 二、堆排序 2.1 调整算法 2.1.2 向上调整算法 2.1.3 向下调整算法 2.2 建堆排序 一、选择排序 1.1 什么是选择排序…...
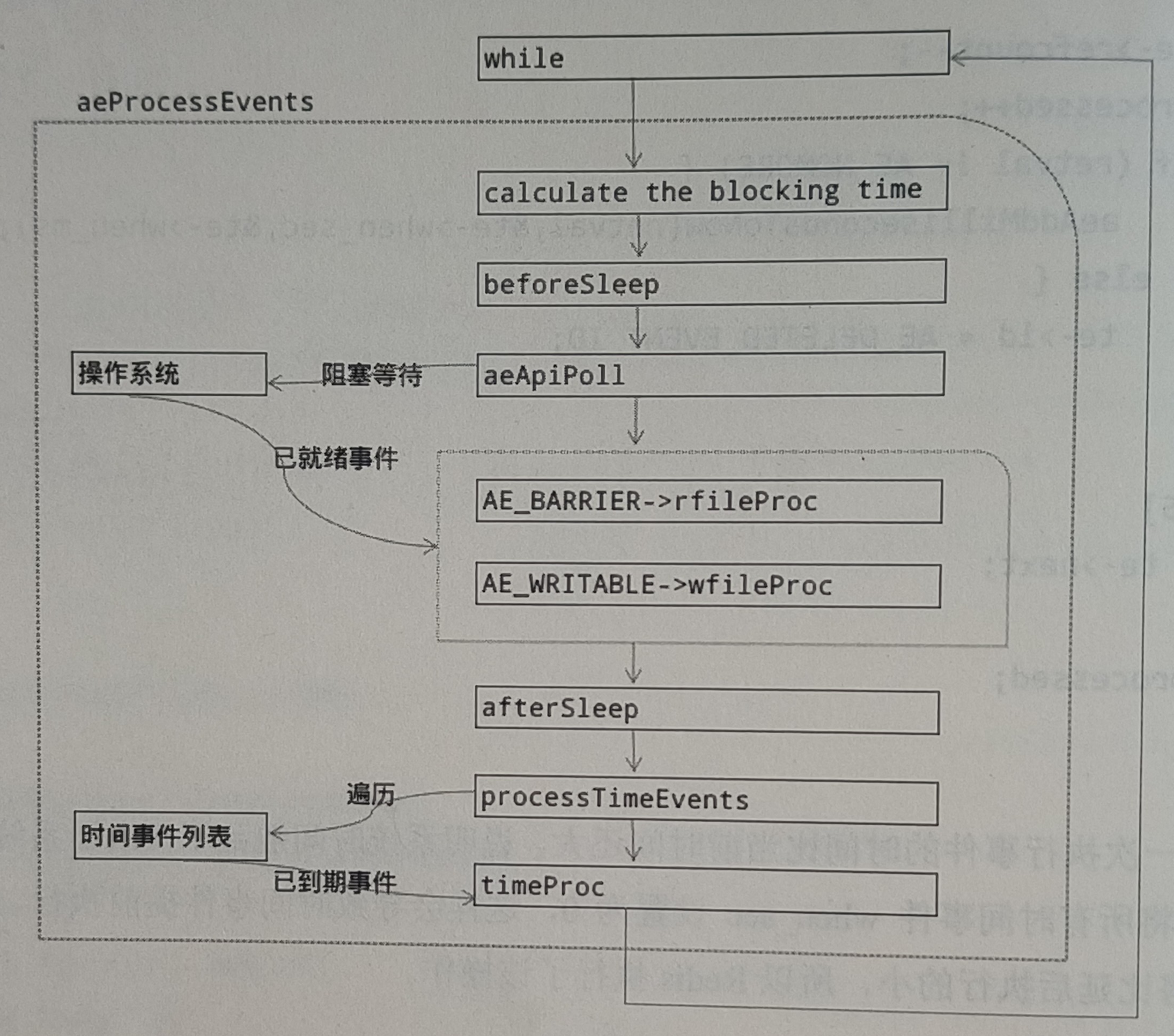
Redis 事件机制 - AE 抽象层
Redis 服务器是一个事件驱动程序,它主要处理如下两种事件: 文件事件:利用 I/O 复用机制,监听 Socket 等文件描述符上发生的事件。这类事件主要由客户端(或其他Redis 服务器)发送网络请求触发。时间事件&am…...
Java | Leetcode Java题解之第118题杨辉三角
题目: 题解: class Solution {public List<List<Integer>> generate(int numRows) {List<List<Integer>> ret new ArrayList<List<Integer>>();for (int i 0; i < numRows; i) {List<Integer> row new…...

DNS 解析过程
文章目录 简介特点查询方式⚡️1. 浏览器缓存2. 系统缓存(hosts文件)3. 路由器缓存4. 本地域名服务器5. 根域名服务器6. 顶级域名服务器7. 权限域名服务器8. 本地域名服务器缓存并返回9. 操作系统缓存并返回10. 浏览器缓存并访问流程图 总结 简介 DNS&a…...

Golang | Leetcode Golang题解之第118题杨辉三角
题目: 题解: func generate(numRows int) [][]int {ans : make([][]int, numRows)for i : range ans {ans[i] make([]int, i1)ans[i][0] 1ans[i][i] 1for j : 1; j < i; j {ans[i][j] ans[i-1][j] ans[i-1][j-1]}}return ans }...

操作系统实验——线程与进程
如果代码或文章中,有什么错误或疑惑,欢迎交流沟通哦~ ## 进程与线程的区别 1. **各自定义**: 进程是操作系统进行资源分配和调度的一个独立单位,具有一定独立功能的程序关于某个数据集合的依次运行活动。 线程被称为轻量级的进程…...
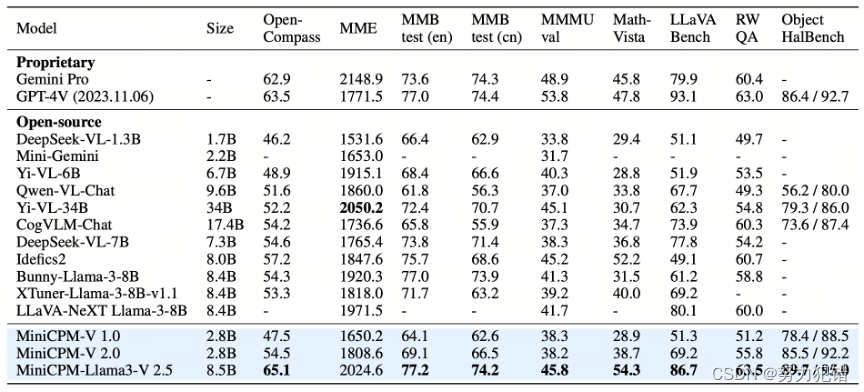
最强端侧多模态模型MiniCPM-V 2.5,8B 参数,性能超越 GPT-4V 和 Gemini Pro
前言 近年来,人工智能领域掀起了一股大模型热潮,然而大模型的巨大参数量级和高昂的算力需求,限制了其在端侧设备上的应用。为了打破这一局限,面壁智能推出了 MiniCPM 模型家族,致力于打造高性能、低参数量的端侧模型。…...
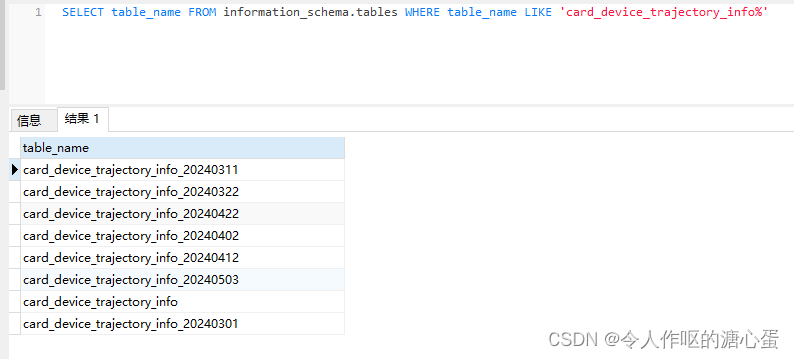
Spring Boot中如何查询PGSQL分表后的数据
数据库用的pgsql,在表数据超过100w条的时候执行定时任务进行了分表,分表后表名命名为原的表名后面拼接时间,如原表名是card_device_trajectory_info,分表后拼接时间后得到card_device_trajectory_info_20240503,然后分…...

如何学习一个新技能
1. 提出想法 2.找到学习方法,学习路径 3.开始学 参考视频:如何成为超速学习者?快速学会任何新技能!_哔哩哔哩_bilibili...

sklearn之logistic回归
文章目录 logistic回归logit logistic回归 logistic regression被称之为logistic回归,对于logistic这个单词来说,他本身的翻译其实不太容易,比较有名的译法是对数几率回归,我也认为这种译法是比较合适的,虽然并非logi…...
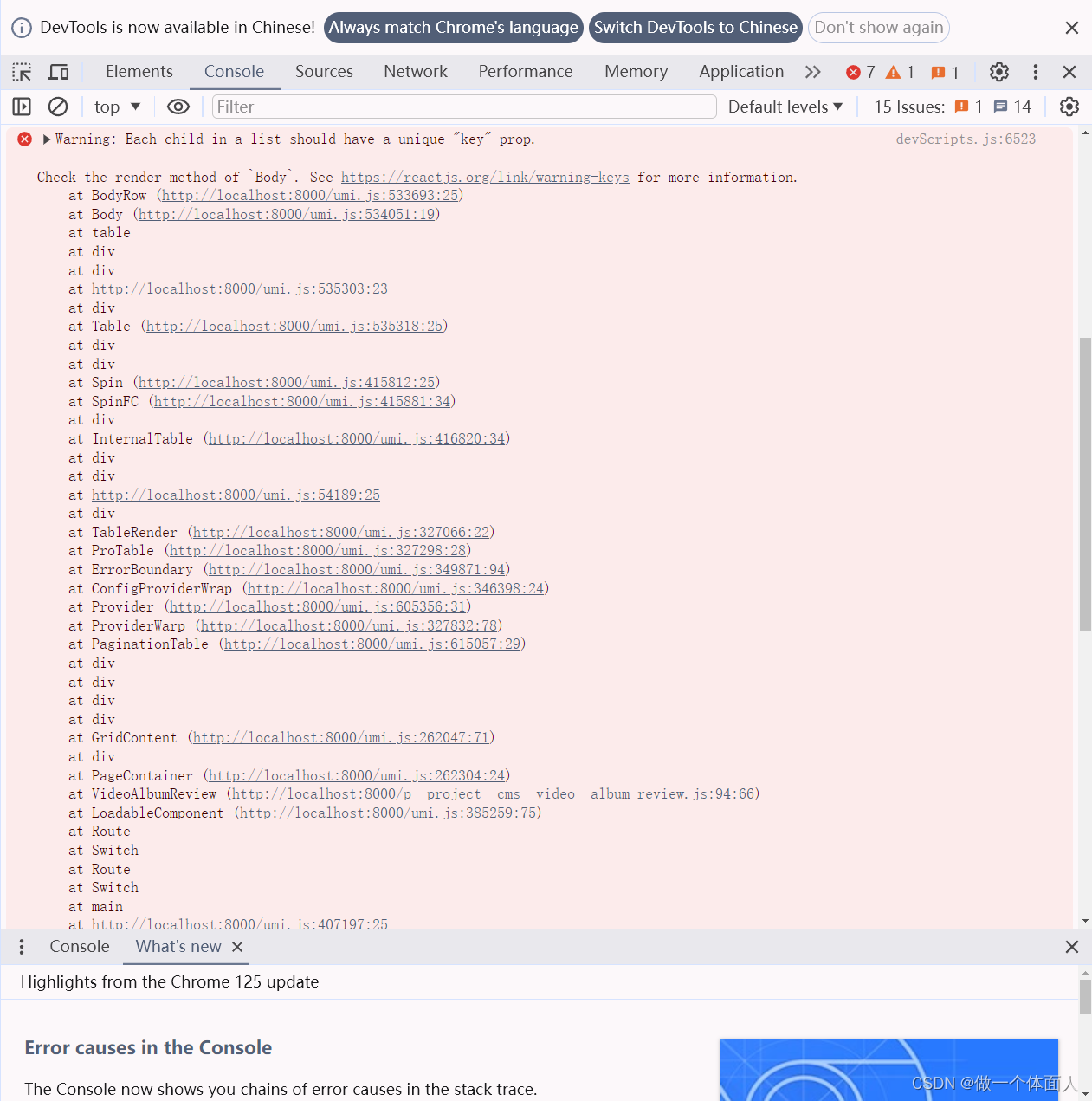
Warning: Each child in a list should have a unique “key“ prop.
问题描述: 使用ProTable的时候,报错如下 原因分析: 根据报错内容可以分析出,表格数据缺少唯一key, <PaginationTablecolumns{columns}pagination{{pageSize: 10,current: 1,showSizeChanger: true,showQuickJum…...
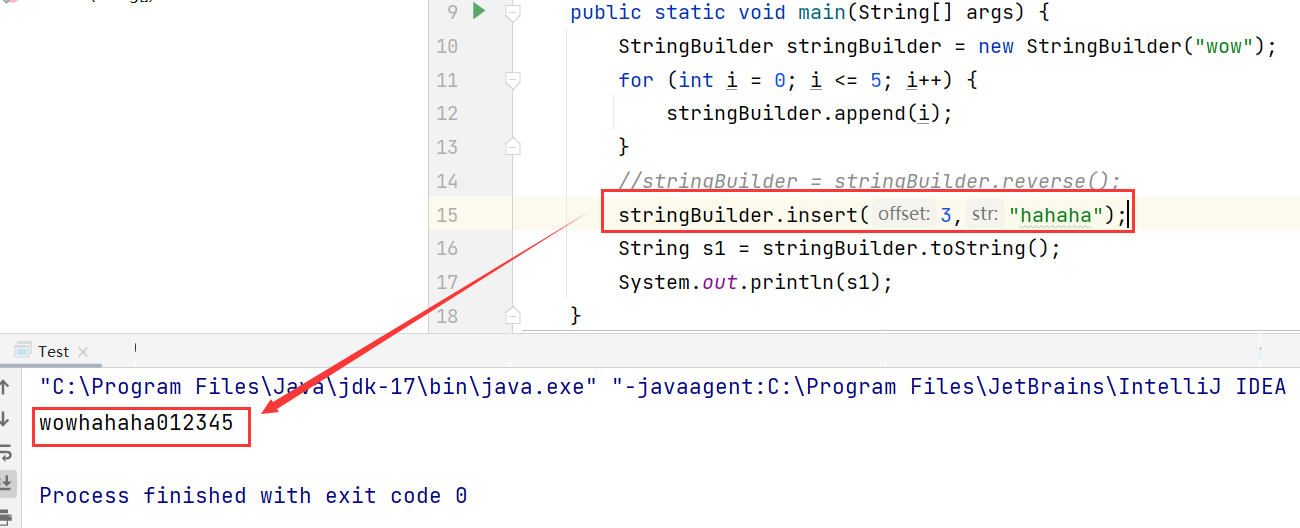
JavaSE:StringBuilder和StringBuffer类
1、引言 在上一篇文章中,我们理解了字符串的常用方法,细心的同学大概已经发现,不管是将字符串中的字符转变为大写或小写,或是完成字符串的替换,又或是去除空白字符等等,只要涉及到字符串的修改,…...

C语言在线编程网站:探索编程的奥秘与深度
C语言在线编程网站:探索编程的奥秘与深度 在数字世界的浩瀚海洋中,编程已成为连接现实与虚拟的桥梁。而C语言,作为编程领域的经典之作,其深度与广度令无数探索者着迷。为了满足广大编程爱好者的需求,C语言在线编程网站…...

Android 之广播监听网络变化
网络状态变化监听帮助类 NetBroadcastReceiverHelper public class NetBroadcastReceiverHelper {private static final String TAG "NetBroadcastReceiverHelper";private static final String NET_CHANGE_ACTION "android.net.conn.CONNECTIVITY_CHANGE&qu…...
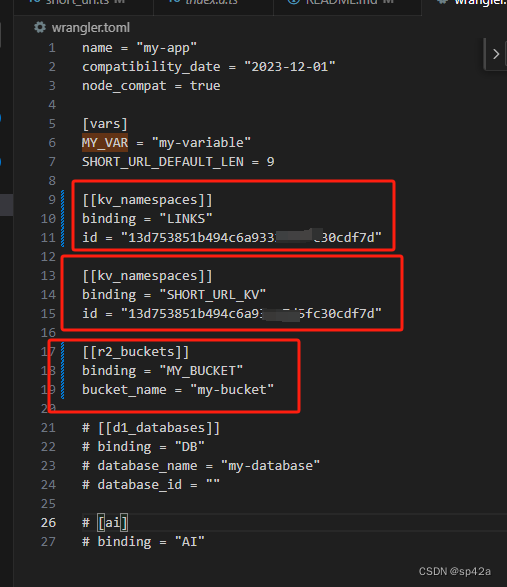
Hono 框架使用经验谈
Hono🔥是一个小型、快速并开源的 Serverless Web 框架,用 TypeScript 写就。它适用于任何JavaScript运行时:Cloudflare Workers,Fastly ComputeEdge,Deno,Bun,Vercel,Netlify&#x…...

mac 下配置mysql的全局环境变量
前言 如果你还没有安装mysql,请参考这篇文章手把手教你MAC本地数据库的安装与使用:mysql python (pymysql)【一】 - 知乎 正文 1.打开终端,输入命令”echo $SHELL“,显示当前的shell ⚠️本人使用的终端shell是zsh,如果你使用…...

小红书云原生 Kafka 技术剖析:分层存储与弹性伸缩
面对 Kafka 规模快速增长带来的成本、效率和稳定性挑战时,小红书大数据存储团队采取云原生架构实践:通过引入冷热数据分层存储、容器化技术以及自研的负载均衡服务「Balance Control」,成功实现了集群存储成本的显著降低、分钟级的集群弹性迁…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...
