sklearn之logistic回归
文章目录
- logistic回归
- logit
logistic回归
logistic regression被称之为logistic回归,对于logistic这个单词来说,他本身的翻译其实不太容易,比较有名的译法是对数几率回归,我也认为这种译法是比较合适的,虽然并非logistic的本意,但却是最贴切这个算法本身的译法
regression的意思是回归,但其实这个算法是一种分类算法
回到我们讲线性回归的时候,主要是对指数本身进行预测,但是想要更实用的话,我们其实更希望知道涨跌的情况,那其实这样的输出值就只有两类,涨或者跌,也就是二分类问题
这种情况其实非常常见,例如销售额和顾客买不买之间的问题,播放量和用户会不会点击的问题
但问题在于,我们统计出来的样本特征往往是一个连续的实数值,而目标则是一个0或1的问题,那么我们简单的线性回归模型就会失效,难以再进行有效的预测
如果直接拟合比较困难,那我们可以将输出值变化一下,从一个非0即1的问题变成涨跌的概率问题,那么概率是连续值,我们就又回到了从连续值到连续值的映射,这似乎就还是回归的内容
那我们给出一个阈值( θ \theta θ),当概率大于阈值时,认为涨的可能性大,当概率小于阈值时,认为跌的可能性大
用最直觉的想法,就是涨的概率大于不涨的概率就可以了,那么我们就可以设涨的概率是 P P P,不涨的概率就是 1 − P 1-P 1−P
当 P 1 − P > 1 \frac{P}{1-P}>1 1−PP>1时,就可以认为涨的可能性大
这个公式其实就是odds几率,接下来我们需要把观察的连续值和输出的连续值用数学模型联系起来
需要知道的是,假设 x x x表示事件涨, P ( x ) P(x) P(x)表示涨的概率,他的值域是就是 [ 0 , 1 ] [0,1] [0,1],然后我们通过几率的运算,其实得到的就是 o d d s ( x ) odds(x) odds(x),他的值域就变成了 [ 0 , + ∞ ) [0,+\infty) [0,+∞)(因为 o d d s ( x ) = P ( x ) 1 − P ( x ) odds(x)=\frac{P(x)}{1-P(x)} odds(x)=1−P(x)P(x)且 P ( x ) P(x) P(x)的范围是 [ 0 , 1 ] [0,1] [0,1])
logit
odds是几率,他在数学上的定义就是事件发生的概率比事件不发生的概率
logit其实就是给一个数取对数,我们接下来的操作是要给几率取对数,为什么呢
如果不取对数的话odds(x)的值域只有非负的部分,并不满足我们映射到全体实数的需求,因此我们对其再取对数即可,通常我们会取自然对数,并且用z表示logit(odds(x))
z = ln ( P ( x ) 1 − P ( x ) ) z=\ln(\frac{P(x)}{1-P(x)}) z=ln(1−P(x)P(x))
需要注意的是这里的小写z本质上仍然是几率,或者说是直接与几率相关的
那我们就可以轻松的反推出概率P的值 P = e z 1 + e z P=\frac{e^z}{1+e^z} P=1+ezez
然后再对这个式子做简单的变化,积分,就可以求出他的概率分布函数 P ( Z ≤ z ) = 1 1 + e z P(Z\leq z)=\frac{1}{1+e^z} P(Z≤z)=1+ez1
这里的大写Z表示的就是随机变量,取值为实数
这个公式称之为sigmoid函数,logistic函数,具有单调增,处处可导的性质
这个函数可以将任意实数的值映射到0到1之间,这个特性对于解决二分类问题十分重要,阈值也就可以在这里面选了
相关文章:

sklearn之logistic回归
文章目录 logistic回归logit logistic回归 logistic regression被称之为logistic回归,对于logistic这个单词来说,他本身的翻译其实不太容易,比较有名的译法是对数几率回归,我也认为这种译法是比较合适的,虽然并非logi…...
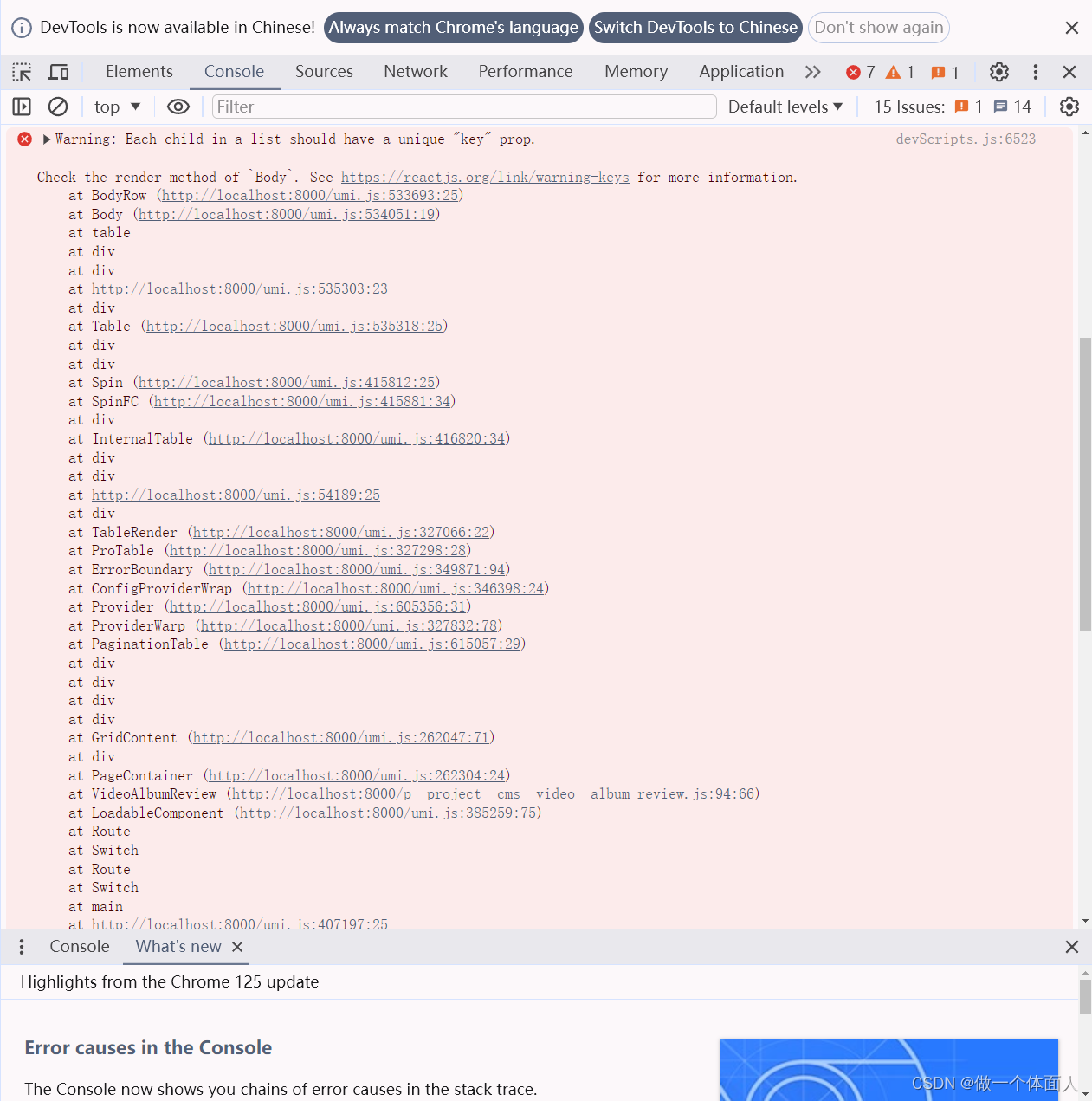
Warning: Each child in a list should have a unique “key“ prop.
问题描述: 使用ProTable的时候,报错如下 原因分析: 根据报错内容可以分析出,表格数据缺少唯一key, <PaginationTablecolumns{columns}pagination{{pageSize: 10,current: 1,showSizeChanger: true,showQuickJum…...
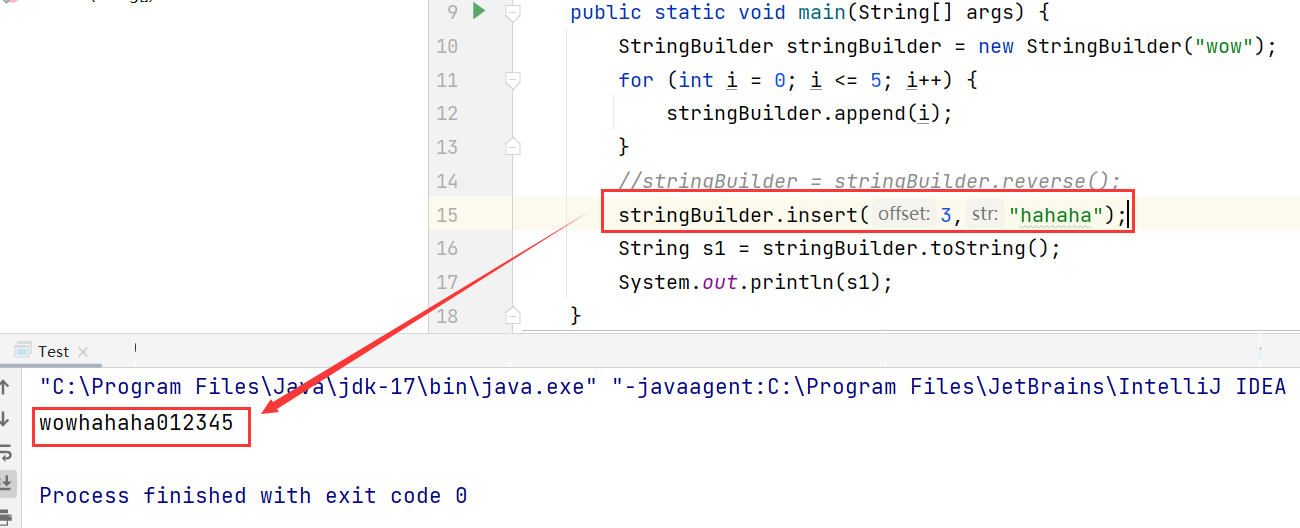
JavaSE:StringBuilder和StringBuffer类
1、引言 在上一篇文章中,我们理解了字符串的常用方法,细心的同学大概已经发现,不管是将字符串中的字符转变为大写或小写,或是完成字符串的替换,又或是去除空白字符等等,只要涉及到字符串的修改,…...

C语言在线编程网站:探索编程的奥秘与深度
C语言在线编程网站:探索编程的奥秘与深度 在数字世界的浩瀚海洋中,编程已成为连接现实与虚拟的桥梁。而C语言,作为编程领域的经典之作,其深度与广度令无数探索者着迷。为了满足广大编程爱好者的需求,C语言在线编程网站…...

Android 之广播监听网络变化
网络状态变化监听帮助类 NetBroadcastReceiverHelper public class NetBroadcastReceiverHelper {private static final String TAG "NetBroadcastReceiverHelper";private static final String NET_CHANGE_ACTION "android.net.conn.CONNECTIVITY_CHANGE&qu…...
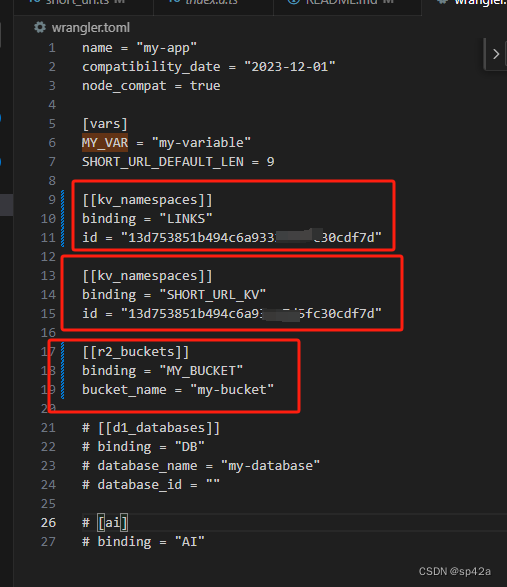
Hono 框架使用经验谈
Hono🔥是一个小型、快速并开源的 Serverless Web 框架,用 TypeScript 写就。它适用于任何JavaScript运行时:Cloudflare Workers,Fastly ComputeEdge,Deno,Bun,Vercel,Netlify&#x…...

mac 下配置mysql的全局环境变量
前言 如果你还没有安装mysql,请参考这篇文章手把手教你MAC本地数据库的安装与使用:mysql python (pymysql)【一】 - 知乎 正文 1.打开终端,输入命令”echo $SHELL“,显示当前的shell ⚠️本人使用的终端shell是zsh,如果你使用…...

小红书云原生 Kafka 技术剖析:分层存储与弹性伸缩
面对 Kafka 规模快速增长带来的成本、效率和稳定性挑战时,小红书大数据存储团队采取云原生架构实践:通过引入冷热数据分层存储、容器化技术以及自研的负载均衡服务「Balance Control」,成功实现了集群存储成本的显著降低、分钟级的集群弹性迁…...

Python实现解码二进制数据以匹配给定的C++结构体
要在Python中实现解码二进制数据以匹配给定的C结构体Ytest,你需要了解每个字段在结构体中的偏移量(由于结构体内存对齐,这些偏移量可能与字段的顺序和大小不完全对应)。不过,在没有指定内存对齐的情况下,我…...
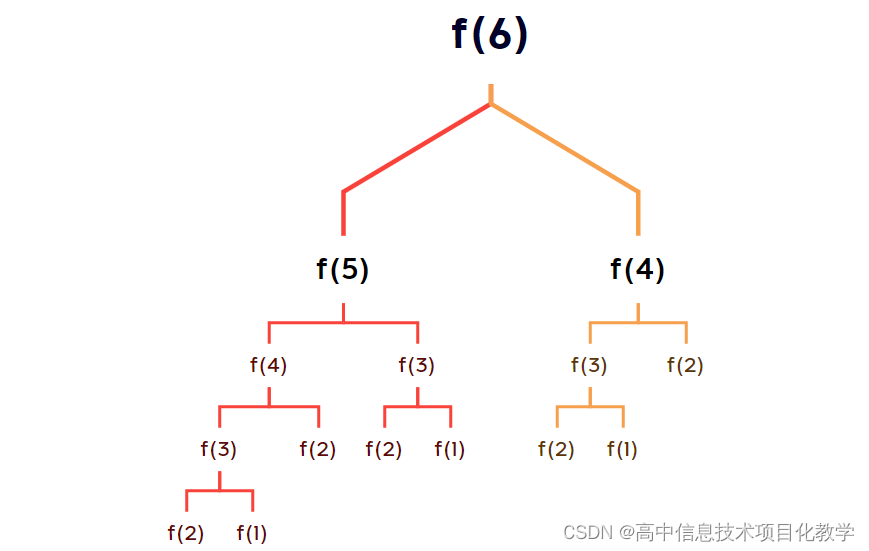
实施阶段(2024年5月)
【项目活动1】斐波拉契数列第n项的值? 数学思想:第一项和第二项的值都为1,从第三项开始值为前两项的和。 方法一:迭代 迭代变量:f1和f2 迭代表达式:f1,f2f2,f1f2 计数器:i 迭代表达式运算…...
 Object Pascal 学习笔记---第13章第3节 (弱引用是系统托管的 ))
(delphi11最新学习资料) Object Pascal 学习笔记---第13章第3节 (弱引用是系统托管的 )
13.4.2 弱引用是系统托管的 弱引用的托管是一个非常重要的内容。换句话说,系统会在内存中保存一个弱引用列表,当对象被销毁时,系统会检查是否有任何弱引用指向该对象,如果有,系统会将实际引用赋值为 nil࿰…...

安装WordPress
第 1 步:下载并解压 wget https://wordpress.org/latest.tar.gz 然后使用以下命令提取包: tar -xzvf latest.tar.gz 第 2 步:创建数据库 比如数据库名称为wordpress,编码格式为 utf8mb4_general_ci 第 3 步:设置wp-con…...

【STL库源码剖析】list 简单实现
从此音尘各悄然 春山如黛草如烟 目录 list 的结点设计 list 的迭代器 list 的部分框架 迭代器的实现 容量相关相关函数 实现 insert 在指定位置插入 val 实现 push_back 在尾部进行插入 实现 erase 在指定位置删除 实现 pop_back 在尾部进行删除 实现 list 的头插、头删 实现…...

web前端框架设计第十一课-常用插件
web前端框架设计第十一课-常用插件 一.预习笔记 1.路由的基础使用 2.动态路由 3.嵌套路由 二.课堂笔记 三.课后回顾 –行动是治愈恐惧的良药,犹豫拖延将不断滋养恐惧...
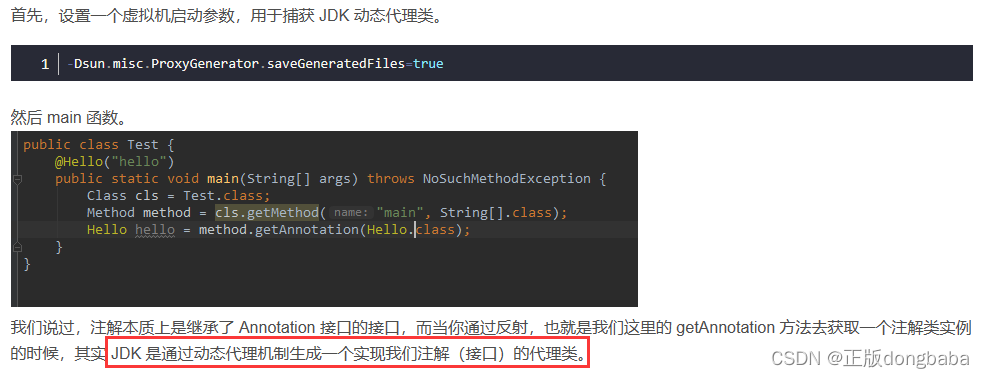
Java基础-注解
注解本质是继承了Annotation接口的一个接口 首先,我们通过键值对的形式可以为注解属性赋值,像这样:Hello(value “hello”)。 接着,你用注解修饰某个元素,编译器将在编译期扫描每个类或者方…...

SpringCloud之SSO单点登录-基于Gateway和OAuth2的跨系统统一认证和鉴权详解
单点登录(SSO)是一种身份验证过程,允许用户通过一次登录访问多个系统。本文将深入解析单点登录的原理,并详细介绍如何在Spring Cloud环境中实现单点登录。通过具体的架构图和代码示例,我们将展示SSO的工作机制和优势&a…...
原创)
二分查找算法详讲(三种版本写法)原创
介绍: 二分查找算法(Binary Search)是一种在有序数组中查找目标元素的算法。 它的基本思想是通过将目标元素与数组的中间元素进行比较,从而将搜索范围缩小一半。 如果目标元素等于中间元素,则搜索结束;如果目标元素小…...
之commit之前自动执行脚本)
Git钩子(Hooks)之commit之前自动执行脚本
介绍 官方文档: 英文:https://git-scm.com/book/en/v2/Customizing-Git-Git-Hooks中文:https://git-scm.com/book/zh/v2/自定义-Git-Git-钩子 下面只复制了pre-commit部分文档,其他详见官方文档。 Git Hooks Like many other…...

nano机器人2:机械臂的视觉抓取
前言 参考链接: 【机械臂入门教程】机械臂视觉抓取从理论到实战 GRCNN 通过神经网络,先进行模型训练,在进行模型评估。 机械臂逆运动学求解 所有串联型6自由度机械臂均是可解的,但这种解通常只能通过数值解法得到,计算难度大&am…...

技术速递|宣布 Java on Azure 开发工具支持 Java on Azure Container Apps
作者:Jialuo Gan 排版:Alan Wang 在 Microsoft Build 2024 期间宣布,Azure Container Apps 现在可为 Java 开发人员提供丰富的操作功能。(详细内容请参见本博客)。 我们很高兴地与大家分享,Azure Toolkit for Intelli…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...
运行vue项目报错 errors and 0 warnings potentially fixable with the `--fix` option.
报错 找到package.json文件 找到这个修改成 "lint": "eslint --fix --ext .js,.vue src" 为elsint有配置结尾换行符,最后运行:npm run lint --fix...
