[LitCTF 2023]yafu (中级) (素数分解)
题目:
from Crypto.Util.number import *
from secret import flagm = bytes_to_long(flag)
n = 1
for i in range(15):n *=getPrime(32)
e = 65537
c = pow(m,e,n)
print(f'n = {n}')
print(f'c = {c}')n = 15241208217768849887180010139590210767831431018204645415681695749294131435566140166245881287131522331092026252879324931622292179726764214435307
c = 12608550100856399369399391849907846147170257754920996952259023159548789970041433744454761458030776176806265496305629236559551086998780836655717题目叫yafu,我们知道yafu是用来分解大素数的,故我们将n分解。
法一:我们可以采用在线网站分解factordb.com
分解之后我们直接将挨个输如到EXP中,然后计算phi:(p1-1)*(p2-1)*....*(pn-1).最后正常解出即可。
法二:我们使用python脚本分解
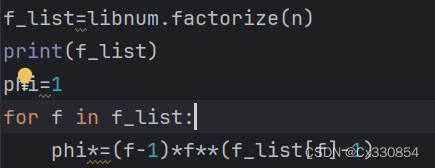
f_list=libnum.factorize(n)
输出结果如下![]()
冒号前的数是分解出来的素数,第二个数是该数出现的次数。
然后我们利用欧拉函数计算phi:若n = p^k,其中 p 是质数,k 是正整数,那么 φ(n) = p^(k-1) * (p-1)。当出现次数为1时,即k=1,p^(k-1)=1.与一般式同
EXP:
from Cryptodome.Util.number import *
import libnum
from gmpy2 import gmpy2e = 65537
n = 15241208217768849887180010139590210767831431018204645415681695749294131435566140166245881287131522331092026252879324931622292179726764214435307
c = 12608550100856399369399391849907846147170257754920996952259023159548789970041433744454761458030776176806265496305629236559551086998780836655717
f_list=libnum.factorize(n)
print(f_list)
phi=1
for f in f_list:phi*=(f-1)*f**(f_list[f]-1)
d=gmpy2.invert(e,phi)
print(long_to_bytes(pow(c,d,n)))相关文章:

[LitCTF 2023]yafu (中级) (素数分解)
题目: from Crypto.Util.number import * from secret import flagm bytes_to_long(flag) n 1 for i in range(15):n *getPrime(32) e 65537 c pow(m,e,n) print(fn {n}) print(fc {c})n 152412082177688498871800101395902107678314310182046454156816957…...

MySQL alter 语句
ALTER TABLE user ADD COLUMN cdkey varchar(255) CHARACTER SET utf8mb4 COLLATE utf8mb4_bin NULL DEFAULT NULL COMMENT CD-Key, ADD COLUMN erp_userid varchar(255) CHARACTER SET utf8mb4 COLLATE utf8mb4_bin NULL DEFAULT NULL COMMENT ERP用户ID, ADD UNIQUE INDEX un…...
python)
列表推导式(解析式)python
Python中的列表推导式(list comprehension)是一种简洁且强大的语法,用于创建新的列表。它允许你通过对现有列表中的元素进行操作或筛选来快速生成新列表。以下是列表推导式的基本语法和一些示例: 基本语法: new_list…...
YOLO-10更快、更强
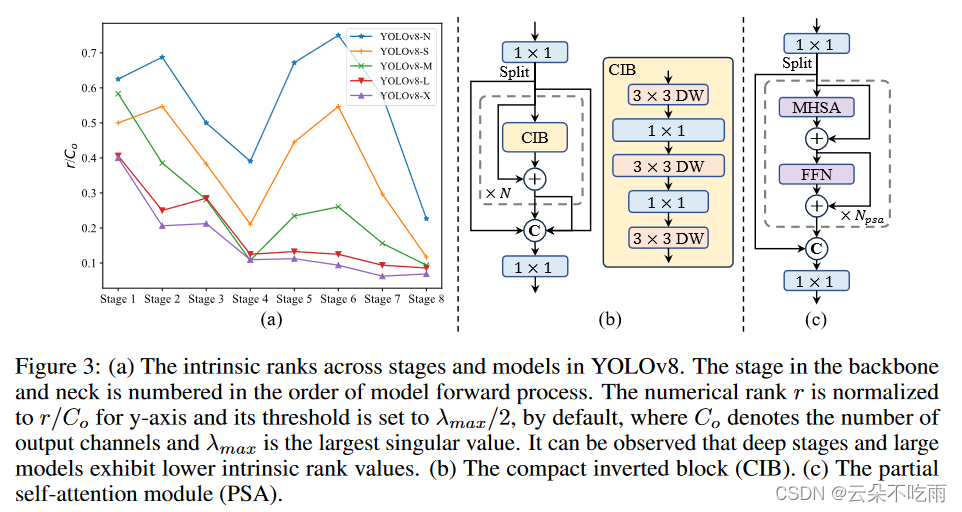
YOLO-10简介 主要贡献: 无NMS的一致双分配 YOLOv10提出了一种通过双标签分配而不用非极大值抑制NMS的策略。这种方法结合了一对多和一对一分配策略的优势,提高了效率并保持了性能。 高效的网络设计 轻量化分类头:在不显著影响性能的情况下&a…...

新火种AI|寻求合作伙伴,展开豪赌,推出神秘AI项目...苹果能否突破AI困境?
作者:小岩 编辑:彩云 2024年,伴随着AI技术的多次爆火,不仅各大科技巨头纷纷进入AI赛道展开角力,诸多智能手机厂商也纷纷加紧布局相关技术,推出众多AI手机。作为手机领域的龙头老大,苹果自然是…...

MFC工控项目实例一主菜单制作
1、本项目用在WIN10下安装的vc6.0兼容版实现。创建项目名为SEAL_PRESSURE的MFC对话框。在项目res文件下添加相关256色ico格式图片。 2、项目名称:密封压力试验机 主菜单名称: 系统参数 SYS_DATA 系统测试 SYS_TEST 选择型号 TYP_CHOICE 开始试验 TES_STA…...

代码随想录-Day22
235. 二叉搜索树的最近公共祖先 方法一:两次遍历 class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {List<TreeNode> path_p getPath(root, p);List<TreeNode> path_q getPath(root, q);TreeNode anc…...

uniapp项目 使用vue-plugin-hiprint静默打印功能
插件地址:https://toscode.mulanos.cn/gyy155/vue-plugin-hiprint h5项目使用插件的静默打印功能 1.下载vue-plugin-hiprint和jquery npm install vue-plugin-hiprint npm install jquery --save2.在mian.js引入插件和jqerry //引入vue-plugin-hiprint import { h…...
视频汇聚EasyCVR视频监控平台GA/T 1400协议特点及应用领域解析
GA/T 1400协议,也被称为视图库标准,全称为《公安视频图像信息应用系统》。这一标准在公安系统中具有举足轻重的地位,它详细规定了公安视频图像信息应用系统的设计原则、系统结构、视频图像信息对象、统一标识编码、系统功能、系统性能、接口协…...

基于似然场的快速避障算法
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言相同思想的采样概率评估快速避障算法前言 认知有限,望大家多多包涵,有什么问题也希望能够与大家多交流,共同成长! 本文先对基于似然场的快速…...

Flutter 中的 IndexedStack 小部件:全面指南
Flutter 中的 IndexedStack 小部件:全面指南 Flutter 是一个功能强大的 UI 框架,它提供了多种方式来构建动态和响应式的用户界面。IndexedStack 是 Flutter 中的一个有趣的小部件,它允许开发者根据索引值来显示一组子元素中的一个。这使得 I…...

基于51单片机的交通灯设计
一.硬件方案 本设计能模拟基本的交通控制系统,用红绿黄灯表示禁行,通行和等待的信号发生,还能进行倒计时显示。按键可以控制禁行、深夜模式、复位、东西通行、南北通行、时间加、时间减、切换等功能。共四个二位阴极数码管,东南西…...

ECMAScript 详解
ECMAScript 详解 ECMAScript(ES)是JavaScript的标准化脚本语言,由ECMA国际通过ECMA-262标准进行规范。ECMAScript定义了语法、类型、对象模型和内置对象等基本特性,是JavaScript、JScript和ActionScript等语言的核心部分。 以下…...
使用Java Swing制作一个飞翔的小鸟游戏
文章目录 一、需求分析二、技术介绍2.1相关技术2.2开发环境 三、功能实现1、开始2、运动3、死亡 四、部分代码实现获取源码 文章最下方获取源码!!! 文章最下方获取源码!!! 文章最下方获取源码!&…...

leetcode 684.冗余连接
思路:并查集 这里的图比较像一种特殊的数据结构,其实也是图论的一种东西,就是基环树,但是这里并不是有向图,而是无向图,所以并不能用那种剪枝操作然后找基环。 看到连通量,我们应该能想到两种…...
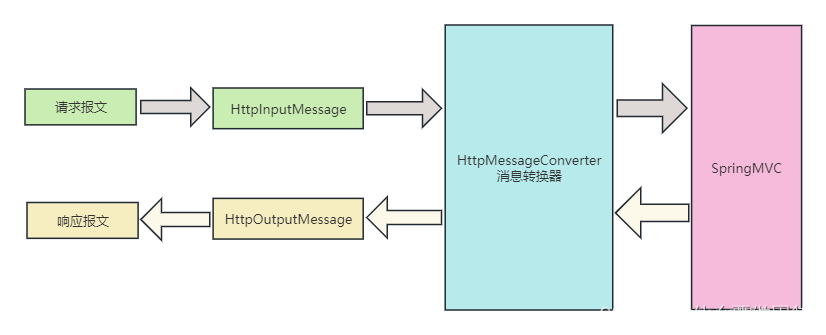
RestTemplet 自定义消息转换器总结
在RestTemplet 请求中,请求发送一个 HTTP 请求时,RestTemplet 会根据请求中的内容类型(Content-Type)选择合适的 HttpMessageConverter 来处理请求体的数据。同样地,当服务器返回一个 HTTP 响应时,RestTemp…...

贝叶斯算法:机器学习中的“黄金法则”与性能提升之道
👀传送门👀 🔍机器学习概述🍀贝叶斯算法原理🚀贝叶斯算法的应用✨文本分类✨医疗系统 💖贝叶斯算法优化✨贝叶斯算法优化的主要步骤✨贝叶斯算法优化的优点✨贝叶斯算法优化的局限性 🚗贝叶斯算…...
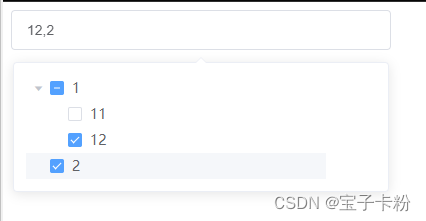
element-ui 实现输入框下拉树组件(2024-05-23)
用element-ui的 el-input,el-tree,el-popover组件组合封装 import url("//unpkg.com/element-ui2.15.14/lib/theme-chalk/index.css"); <script src"//unpkg.com/vue2/dist/vue.js"></script> <script src"//…...

Nginx 相关使用
一、 Nginx 相关使用。 相关命令 启动 nginx start nginx立即停止 nginx nginx -s stop平缓停止 nginx(已有请求不会意外停止) nginx -s quit重新加载配置文件 nginx -s reload二、Nginx conf 配置文件详解 参考文章皮卡丘的猫 server 配置项 server 可…...
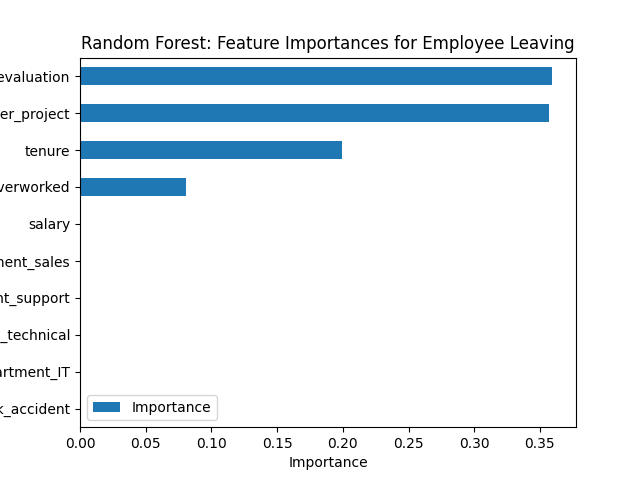
基于Python实现 HR 分析(逻辑回归和基于树的机器学习)【500010104】
介绍 数据集说明 此数据集包含与员工有关的综合属性集合,从人口统计细节到与工作相关的因素。该分析的主要目的是预测员工流动率并辨别导致员工流失的潜在因素。 在这个数据集中,有14,999行,10列,以及这些变量:满意度…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

怎么把自己电脑设置成服务器?
将自己的电脑设置为服务器可以让您托管网站、文件共享或运行各种服务。以下是设置步骤: 基本设置步骤 选择操作系统: Windows:可使用IIS(Internet Information Services)Linux:常用Apache、Nginx等mac…...
