Python高层解雇和客户活跃度量化不确定性模型
🎯要点
🎯量化不确定性模型:🖊模型检测短信编写者行为变化 | 🖊确定(商业领域中)竞争性替代方案 | 🖊确定作弊供词真实比例 | 🖊学生考试作弊 | 🖊确定零部件损坏导致的灾难事故原因 | 🖊马尔可夫链蒙特卡罗算法先验-后验范式可视化 | 🖊聚类寻找信息隐藏源头 | 🖊模型确定和纠正虚假商品星评 | 🖊客户商品价格优化呈现 | 🖊星系位置和椭圆率模拟 | 🖊最大化赌场奖金策略 | 🖊证券分析。
🎯动态分析和常微分方程推理流感传播 | 🎯高层领导被解雇模型预测 | 🎯客户活跃度模型预测 | 🎯热饮冷却非线性模型动态分析 | 🎯多级回归和后分层预测公众人物角逐 | 🎯模型分析专业人士对比机器学习工具的优劣 | 🎯销售领域利润率建模 | 🎯模型分析定位无线网络用户位置。
🍇Python贝叶斯推理
贝叶斯推理是一种找出变量分布的方法(例如高度 h h h 的分布)。贝叶斯推理的有趣特征是,统计学家(或数据科学家)可以利用他们的先验知识作为改进我们对分布情况的猜测的手段。贝叶斯推理依赖于贝叶斯统计的主要公式:贝叶斯定理。贝叶斯定理接受我们对分布的假设,即新的数据,并输出更新后的分布。对于数据科学,贝叶斯定理通常表示如下:
P ( θ ∣ Data ) = P ( Data ∣ θ ) ∗ P ( θ ) P ( Data ) P(\theta \mid \text { Data })=\frac{P(\text { Data } \mid \theta) * P(\theta)}{P(\text { Data })} P(θ∣ Data )=P( Data )P( Data ∣θ)∗P(θ)
- P ( θ ∣ D a t a ) P(\theta \mid D a t a) P(θ∣Data) 后验
- P ( P( P( Data ∣ θ ) \mid \theta) ∣θ) 似然
- P ( θ ) P(\theta) P(θ) 先验
- P ( P( P( Data ) ) ) 事实
我们可以从贝叶斯定理中看出,先验是一个概率:P(θ)。首先,让我们深入研究一下“θ”的含义。θ 通常表示为我们对最能描述我们试图研究的变量的模型的假设。让我们回到身高的例子。根据背景知识和常识,我们推断出身高在一个班级中呈正态分布。正式来说:
h ∼ N ( μ , σ ) h \sim N (\mu, \sigma) h∼N(μ,σ)
其中 N N N表示正态分布, μ \mu μ表示平均值, σ \sigma σ表示标准差。
现在,我们的先验并不完全是上面的表达式。相反,它是我们对每个参数 μ \mu μ 和 σ \sigma σ 如何分布的假设。请注意,这就是贝叶斯统计的定义特征的体现:我们如何找到这些参数的分布?有趣的是,我们根据先验知识“编造”它们。如果我们的先验知识很少,我们可以选择一个非常无信息的先验,以免使过程产生偏差。例如,我们可以定义平均高度 μ \mu μ 介于 1.65 m 1.65 m 1.65m 和 1.8 m 1.8 m 1.8m 之间。如果我们想要一个无信息的先验,我们可以说 μ \mu μ 沿着该区间均匀分布。相反,如果我们认为平均高度在某种程度上偏向于更接近 1.65 m 1.65 m 1.65m 而不是 1.8 m 1.8 m 1.8m 的值,我们可以定义 μ \mu μ 服从 beta 分布,由“超”参数 α \alpha α 定义和 β \beta β。我们可以看看下面这些选项:
import scipy.stats as sts
import numpy as np
import matplotlib.pyplot as pltmu = np.linspace(1.65, 1.8, num = 50)
test = np.linspace(0, 2)
uniform_dist = sts.uniform.pdf(mu) + 1
uniform_dist = uniform_dist/uniform_dist.sum()
beta_dist = sts.beta.pdf(mu, 2, 5, loc = 1.65, scale = 0.2)
beta_dist = beta_dist/beta_dist.sum()
plt.plot(mu, beta_dist, label = 'Beta Dist')
plt.plot(mu, uniform_dist, label = 'Uniform Dist')
plt.xlabel("Value of $\mu$ in meters")
plt.ylabel("Probability density")
plt.legend()
请注意 y 轴如何为我们提供“概率密度”,即我们认为真正的 μ \mu μ 是 x x x 轴上的概率密度。另外,请注意,β 分布和均匀分布会导致我们对 μ \mu μ 的值可能得出的不同结论。如果我们选择均匀分布,我们就表示我们不倾向于判断 μ \mu μ 是否接近我们范围内的任何值,我们只是认为它位于其中的某个位置。如果我们选择 beta 分布,我们相当确定 μ \mu μ 的“真实”值介于 1.68 m 1.68 m 1.68m 和 1.72 m 1.72 m 1.72m 之间,如蓝线峰值所示。
请注意,我们正在讨论 μ \mu μ 的先验,但我们的模型实际上有两个参数: N ( μ , σ ) N (\mu, \sigma) N(μ,σ)。一般来说,我们也可以定义 σ \sigma σ 上的先验。然而,如果我们对 σ \sigma σ 的猜测感到幸运,或者如果我们想为了示例而简化过程,我们可以将 σ \sigma σ 设置为固定值,例如 0.1 m 0.1 m 0.1m。
似然表示为 P ( P ( P( Data ∣ θ ) \mid \theta) ∣θ)。在这种情况下,“数据”将是高度的观测值。假设我们要测量一名随机挑选的学生,他们的身高为 1.7m。考虑到有了这个数据,我们现在可以了解 θ \theta θ 的每个选项有多好。我们通过以下问题来做到这一点:如果 θ \theta θ 的一个特定选项(称为 θ 1 \theta 1 θ1)是真实的,那么我们观察到 1.7 m 1.7 m 1.7m 高度的“可能性”有多大? θ 2 \theta 2 θ2 怎么样:如果 θ 2 \theta 2 θ2 是“正确”模型,观察到 1.7 m 1.7 m 1.7m 高度的可能性有多大?
然而,就我们目前的目的而言,我们正在改变分布/模型本身。这意味着我们的 x x x 轴实际上将具有变量 μ \mu μ 的不同可能性,而我们的 y y y 轴将具有每种可能性的概率密度。看看下面的代码,它代表了我们的似然函数及其可视化:
def likelihood_func(datum, mu):likelihood_out = sts.norm.pdf(datum, mu, scale = 0.1) return likelihood_out/likelihood_out.sum()likelihood_out = likelihood_func(1.7, mu)plt.plot(mu, likelihood_out)
plt.title("Likelihood of $\mu$ given observation 1.7m")
plt.ylabel("Probability Density/Likelihood")
plt.xlabel("Value of $\mu$")
plt.show()
一些统计学家将 P ( P ( P( Data ) ) ) 称为“证据”。这个变量的含义非常简单:它是产生价值数据的概率。然而,这很难直接计算。值得庆幸的是,我们有一个好办法。考虑以下方程:
∫ P ( Data ∣ θ ) ∗ P ( θ ) d θ = P ( Data ) \int P(\text { Data } \mid \theta) * P(\theta) d \theta=P(\text { Data }) ∫P( Data ∣θ)∗P(θ)dθ=P( Data )
贝叶斯定理的右侧 P ( θ ∣ P (\theta \mid P(θ∣ Data) 称为“后验”。这是我们对数据如何分布的后验理解,因为我们目睹了数据,并且我们有先验知识。我们如何得到后验呢?回到方程:
P ( θ ∣ Data ) = P ( Data ∣ θ ) ∗ P ( θ ) P ( Data ) P(\theta \mid \text { Data })=\frac{P(\text { Data } \mid \theta) * P(\theta)}{P(\text { Data })} P(θ∣ Data )=P( Data )P( Data ∣θ)∗P(θ)
那么,第一步是将似然度 (P(Data ∣ θ ) ) \mid \theta)) ∣θ)) 与先验 ( P ( θ ) ) ( P (\theta)) (P(θ)) 相乘:
import scipy as spunnormalized_posterior = likelihood_out * uniform_dist
plt.plot(mu, unnormalized_posterior)
plt.xlabel("$\mu$ in meters")
plt.ylabel("Unnormalized Posterior")
plt.show()
👉参阅一:计算思维
👉参阅二:亚图跨际
相关文章:

Python高层解雇和客户活跃度量化不确定性模型
🎯要点 🎯量化不确定性模型:🖊模型检测短信编写者行为变化 | 🖊确定(商业领域中)竞争性替代方案 | 🖊确定作弊供词真实比例 | 🖊学生考试作弊 | 🖊确定零部件…...
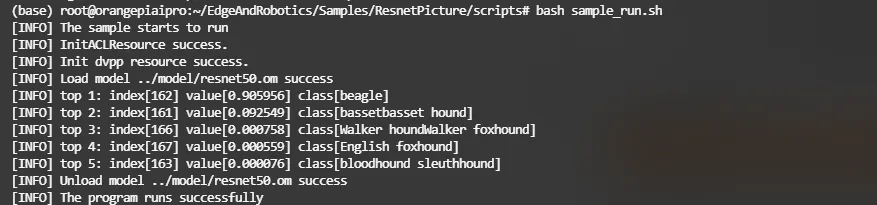
【IOT】OrangePi+HomeAssistant+Yolov5智能家居融合
前言 本文将以OrangePi AIpro为基础,在此基础构建HomeAssistant、YOLO目标检测实现智能家居更加灵活智能的场景实现。 表头表头设备OrangePi AIpro(8T)系统版本Ubuntu 22.04.4 LTSCPU4核64位处理器 AI处理器AI算力AI算力 8TOPS算力接口HDMI2、GPIO接口、Type-C、M.2…...

Python 点云裁剪
点云裁剪 一、介绍1.1 概念1.2 函数讲解二、代码示例2.1 代码实现2.2 代码讲解三、结果示例一、介绍 1.1 概念 点云裁剪 :根据待裁剪对象的多边形体积(json文件)实现点云的裁剪。 1.2 函数讲解 下面代码示例中主要用到了两个函数。 读取待裁剪对象的多边形体积信息(json文…...
)
Presto 从提交SQL到获取结果 源码详解(2)
逻辑执行计划: //进入逻辑执行计划阶段 doAnalyzeQuery().new LogicalPlanner().plan(analysis);//createAnalyzePlan createAnalyzePlan(analysis, (Analyze) statement);//返回RelationPlan,(返回root根节点,逻辑树上包含输出字…...

Python的类全面系统学习
文章目录 1. 基本概念1.1 类(Class)1.2 对象(Object) 2. 类的属性和方法3. 类的继承3.1 继承的概念3.2 单继承3.3 多重继承 4. 方法重写与多态4.1 方法重写4.2 多态 5. 特殊方法与运算符重载5.1 特殊方法(魔法方法&…...
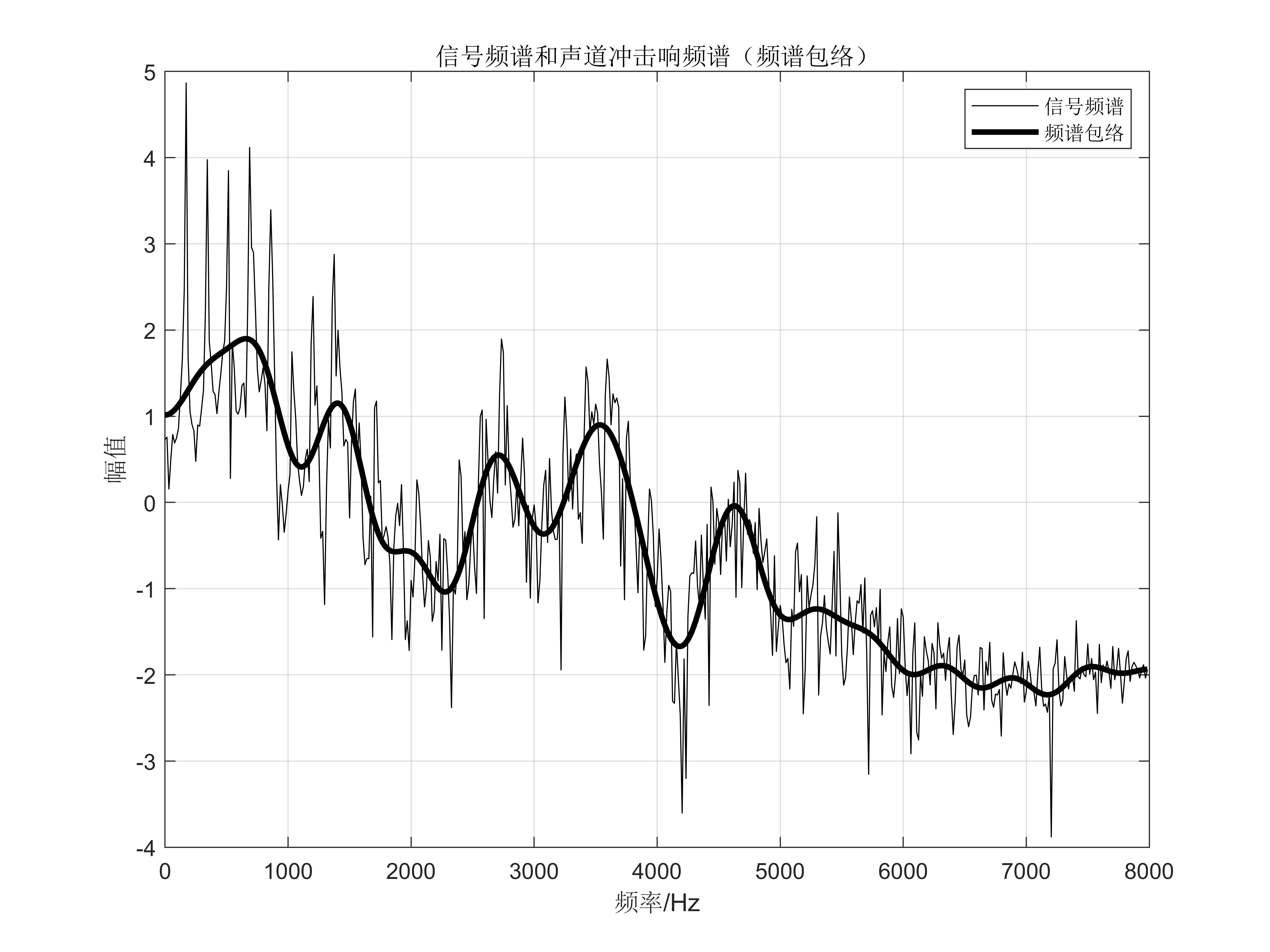
信号处理中简单实用的方法
最小二乘法拟合消除趋势项 消除趋势项函数 在MATLAB的工具箱中已有消除线性趋势项的detrend函数;再介绍以最小二乘法拟合消除趋势项的polydetrend 函数。 函数:detrend功能:消除线性趋势项 调用格式:ydetrend(x) 说明:输入参数x是带有线性趋势项的信号序列,输出…...

Jeecg | 如何解决 ERR Client sent AUTH, but no password is set 问题
最近在尝试Jeecg低代码开发,但是碰到了超级多的问题,不过总归是成功运行起来了。 下面说说碰到的最后一个配置问题:连接redis失败 Error starting ApplicationContext. To display the conditions report re-run your application with deb…...
 更新啦!)
数据容器:set(集合) 更新啦!
数据容器:set(集合) 1.集合的定义方式 {元素, 元素, 元素} # 定义集合 my_set {"欣欣向荣", "嘉嘉", "red", "欣欣向荣", "嘉嘉", "red", "欣欣向荣", "嘉嘉…...
算法入门----小话算法(1)
下面就首先从一些数学问题入手。 Q1: 如何证明时间复杂度O(logN) < O(N) < O(NlogN) < O(N2) < O(2N) < O(N!) < O(NN)? A: 如果一个以整数为参数的不等式不能很容易看出不等的关系,那么最好用图示或者数学归纳法。 很显…...

Vue | 自定义组件双向绑定基础用法
Vue | 自定义组件双向绑定基础用法 vue 中,由于单向数据流,常规的父子组件属性更新,需要 在父组件绑定相应属性,再绑定相应事件,事件里去做更新的操作,利用语法糖 可以减少绑定事件的操作。 这里就简单的梳…...

python使用modbustcp协议与PLC进行简单通信
AI应用开发相关目录 本专栏包括AI应用开发相关内容分享,包括不限于AI算法部署实施细节、AI应用后端分析服务相关概念及开发技巧、AI应用后端应用服务相关概念及开发技巧、AI应用前端实现路径及开发技巧 适用于具备一定算法及Python使用基础的人群 AI应用开发流程概…...

mongodb在游戏开发领域的优势
1、分布式id 游戏服务器里的大部分数据都是要求全局唯一的,例如玩家id,道具id。之所以有这种要求,是因为运营业务上需要进行合服操作,保证不同服的数据在进行合服之后,也能保证id不冲突。如果采用关系型数据库&#x…...

大数据Scala教程从入门到精通第十篇:Scala在IDEA中编写Hello World代码的简单说明
一:代码展示 object Main {def main(args: Array[String]): Unit {//SCALA中可以不写;//绿色的小三角达标的是这个类中有一个MAIN方法代表是可以执行的。//ctrl shift f10可以直接运行println("Hello world!")//Java中的类库我们可以直接使用System.o…...

【SPSS】基于因子分析法对水果茶调查问卷进行分析
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
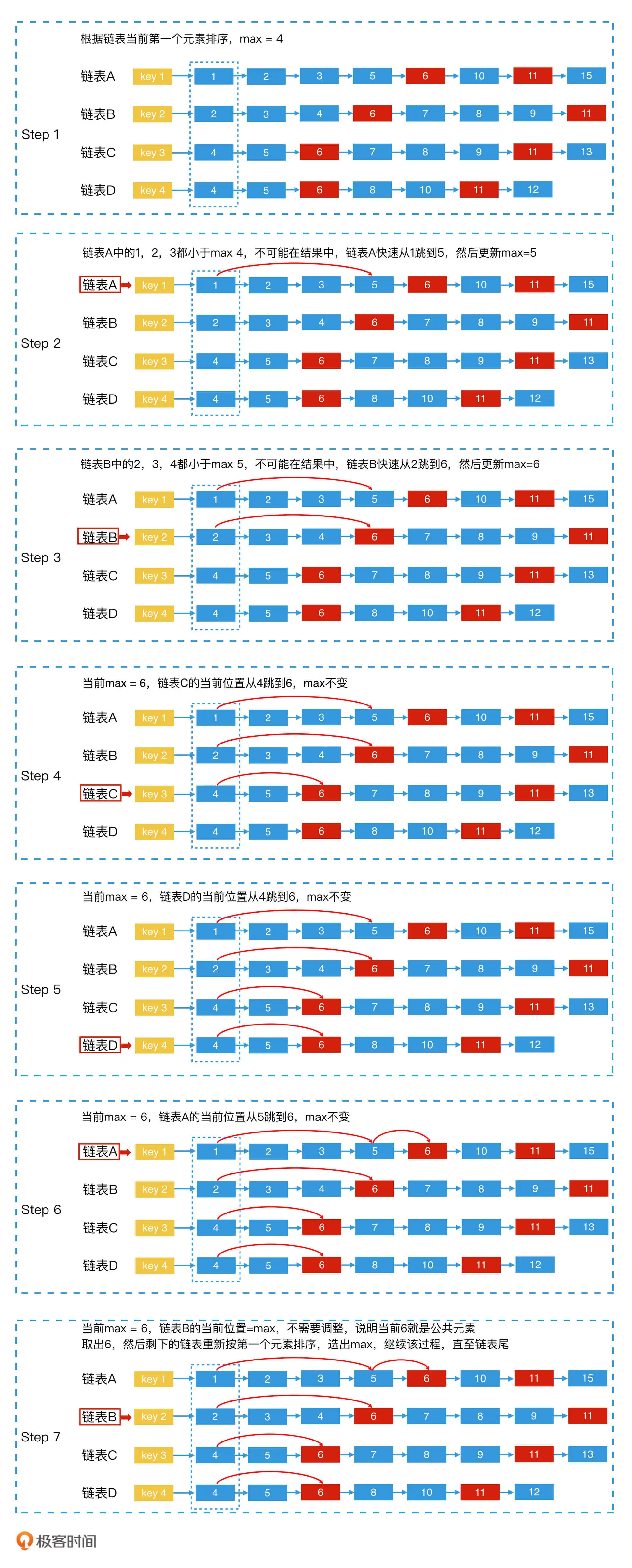
ElasticSearch学习篇12_《检索技术核心20讲》基础篇
背景 学习极客实践课程《检索技术核心20讲》https://time.geekbang.org/column/article/215243 课程分为基础篇、进阶篇、系统案例篇 主要记录企业课程学习过程课程大纲关键点,以文档形式记录笔记。 内容 检索技术:它是更底层的通用技术,…...
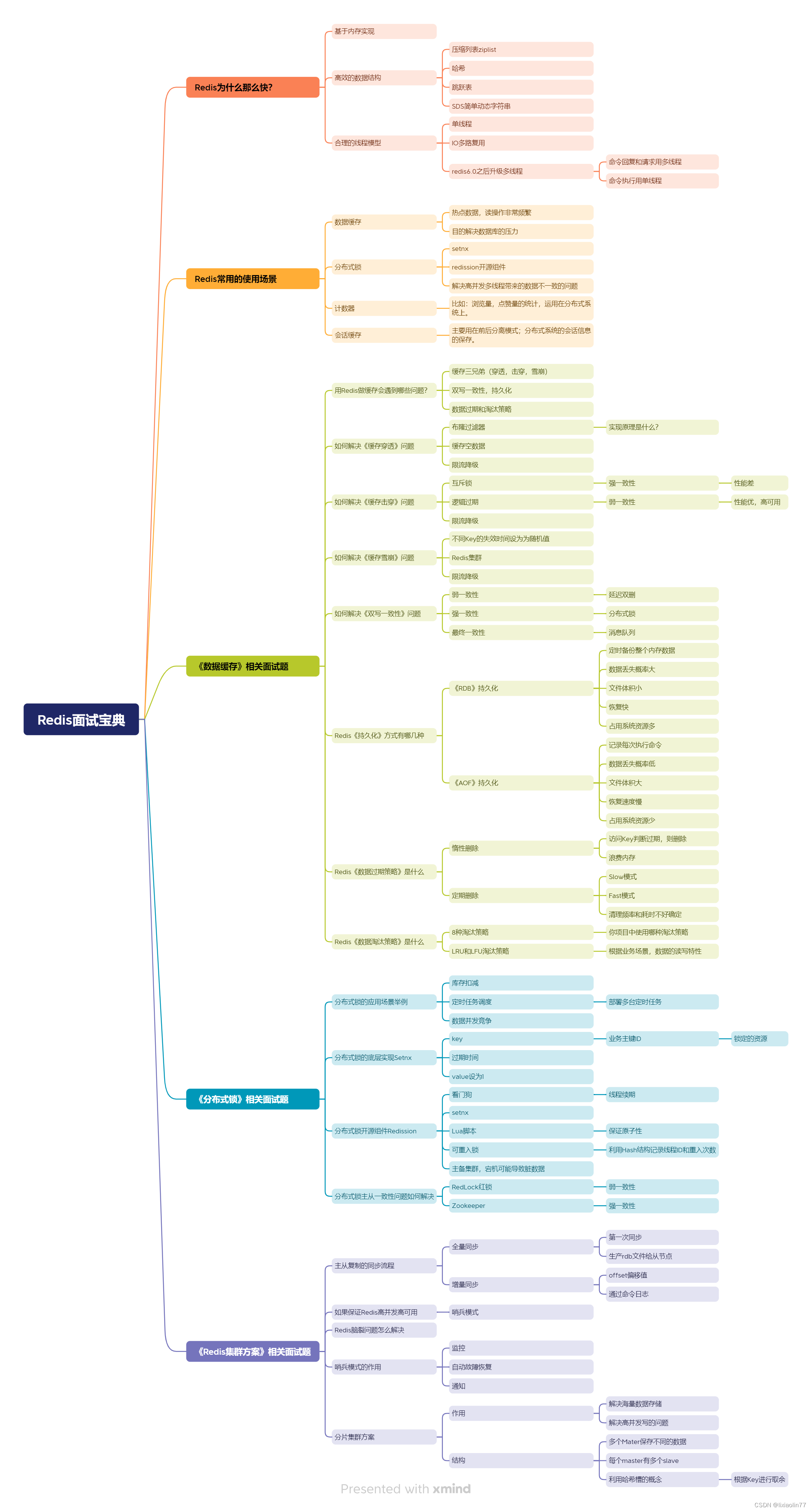
Reids高频面试题汇总总结
一、Redis基础 Redis是什么? Redis是一个开源的内存数据存储系统,它可以用作数据库、缓存和消息中间件。Redis支持多种数据结构,如字符串、哈希表、列表、集合、有序集合等,并提供了丰富的操作命令来操作这些数据结构。Redis的主要特点是什么? 高性能:Redis将数据存储在内…...
19 - grace数据处理 - 补充 - 地下水储量计算过程分解 - 冰后回弹(GIA)改正
19 - grace数据处理 - 补充 - 地下水储量计算过程分解 - 冰后回弹(GIA)改正 0 引言1 gia数据处理过程0 引言 由水量平衡方程可以将地下水储量的计算过程分解为3个部分,第一部分计算陆地水储量变化、第二部分计算地表水储量变化、第三部分计算冰后回弹改正、第四部分计算地下…...
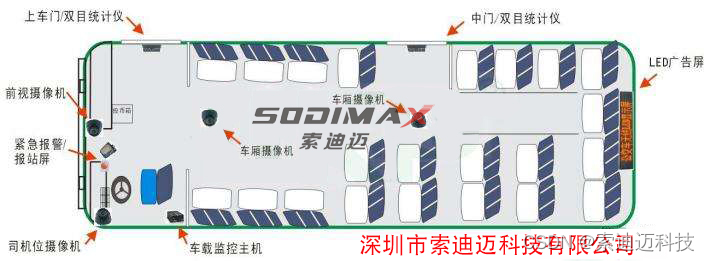
车载客流统计设备:双目3D还原智能统计算法的应用与优势
随着城市交通的日益繁忙和公共交通系统的不断完善,对公交车等交通工具的客流统计和分析变得越来越重要。传统的客流统计方法往往存在效率低下、精度不足等问题,难以满足现代城市交通管理的需求。而基于双目3D还原智能统计算法的车载客流统计设备…...
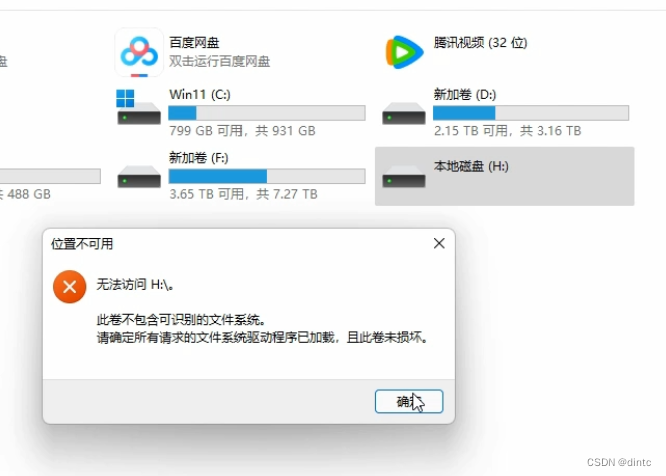
U盘无法打开?数据恢复与预防措施全解析
在日常生活和工作中,U盘已成为我们存储和传输数据的重要工具。然而,有时我们会遇到U盘无法打开的情况,这无疑给我们带来了诸多不便。本文将深入探讨U盘打不开的现象、原因及解决方案,并分享如何预防此类问题的发生。 一、U盘无法访…...

apollo版本更新简要概述
apollo版本更新简要概述 Apollo 里程碑版本9.0重要更新Apollo 开源平台 9.0 的主要新特征如下:基于包管理的 PnC 扩展开发范式基于包管理的感知扩展开发范式全新打造的 Dreamview Plus 开发者工具感知模型全面升级,支持增量训练 版本8.0版本6.0 Apollo 里…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
