软设之排序算法对比
直接插入
时间复杂度:平均情况为O(n^2)。特殊情况下基本有序最优为O(n)
空间复杂度:O(1)
希尔排序
时间复杂度:平均情况O(n^1.3)
空间复杂度:O(1)
直接选择排序
时间复杂度:O(n^2)
空间复杂度:O(1)
堆排序
时间复杂度:O(nlog(2)n)
空间复杂度:O(1)
冒泡排序
时间复杂度:平均情况O(n^2)
空间复杂度:O(1)
快速排序
时间复杂度:平均情况O(nlog(2)n),基本有序最差是O(n^2)
空间复杂度:O(1)
归并排序
时间复杂度 O(nlog(2)n)
空间复杂度O(n)
基数排序
时间复杂度:O(d(n+rd))
空间复杂度:O(rd)
排序算法选择
如果数据元素数目n比较小,可采用直接插入排序和简单选择排序
如果要排列记录基本有序,可以采用直接插入排序或冒泡排序
如果数据数目很大,应采用时间复杂度为O(nlog(2)n)的排序方法。
快速排序目前被认为是内部排序中最好的方法,如果待排序的关键字为随机分布,快速排序的平均运行时间最短
堆排序只需要一个辅助空间,并且不会出现在快速排序中可能出现的最快情况
快速排序和堆排序都是不稳定的排序方法,如果追求排序稳定,可选择归并排序。
相关文章:

软设之排序算法对比
直接插入 时间复杂度:平均情况为O(n^2)。特殊情况下基本有序最优为O(n) 空间复杂度:O(1) 希尔排序 时间复杂度:平均情况O(n^1.3) 空间复杂度:O(1) 直接选择排序 时间复杂度:O(n^2) 空间复杂度:O(1) 堆排序 时间复杂度:O(nlog(2)n) 空间复杂度:O(1) 冒泡排序 时间…...
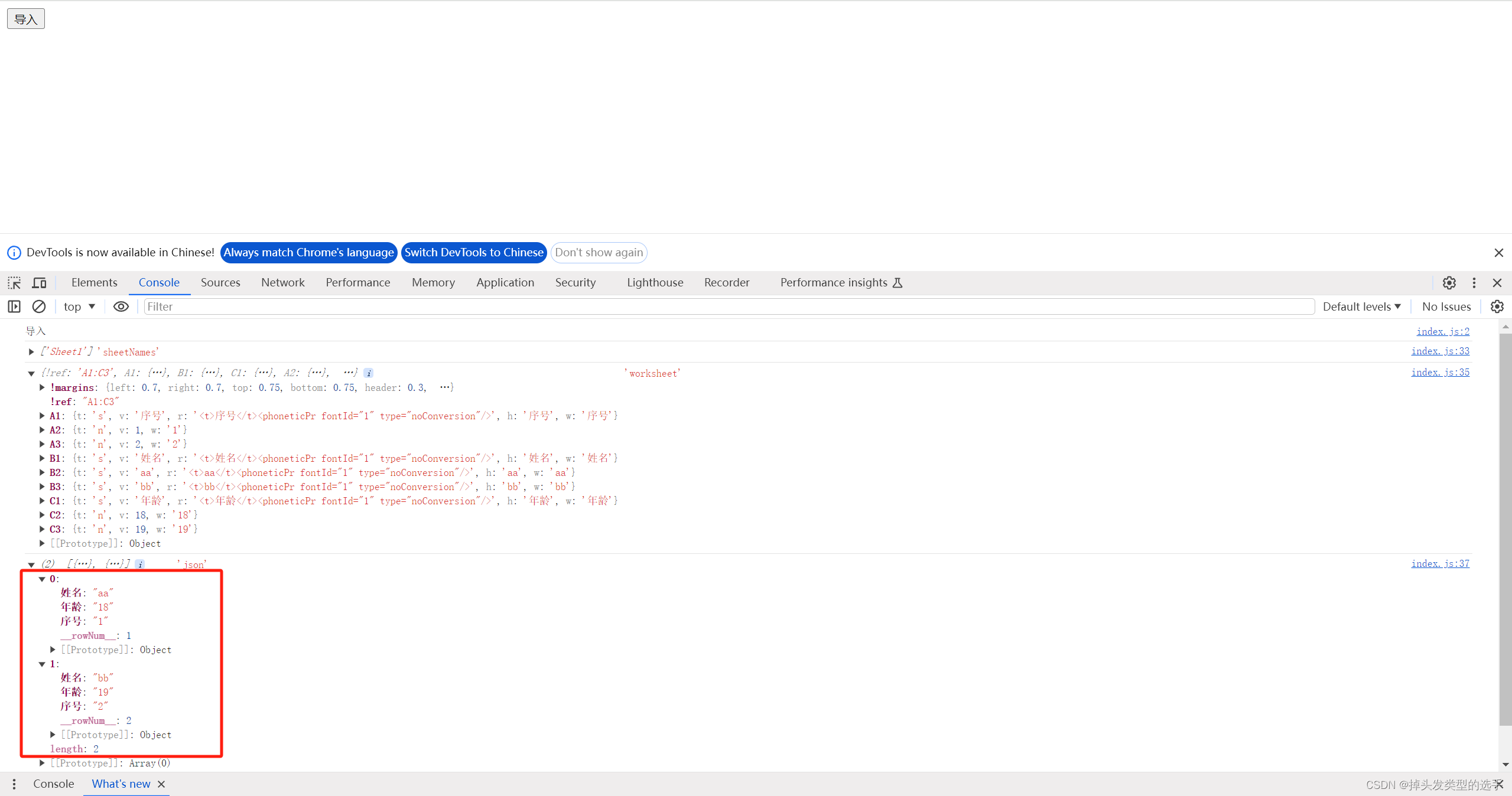
javascript导入excel文件
导入文件用到一个 xlsx.core.js 的包。 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><script type"tex…...

「C系列」C 变量及常见问题梳理
文章目录 一、C 变量1. 整数变量2. 浮点数变量3. 字符变量4. 字符串变量(在C中,通常使用字符数组来表示字符串) 二、C 变量-常见问题1. 变量未初始化2. 变量类型不匹配3. 变量作用域问题4. 变量命名冲突5. 变量越界访问6. 变量声明位置7. 变量…...

<网络安全VIP>第二篇《工业控制软件》
1 PLC PLC,(Programmable Logic Controller),可编程逻辑控制器(PLC)是种专门为在工业环境下应用而设计的数字运算操作电子系统。 2 DCS 四、DCS的发展趋势 一、DCS的基本定义 DCS是分布式控制系统(Distributed Control System)的英文缩写,在国内自控行业又称之为集…...
微服务:Rabbitmq中的不同交换机的使用Fanout、Direct、Topic(消息队列中间件)
文章目录 发布订阅Fanout 交换机Direct 交换机Topic 交换机通配符规则 发布订阅 在这里插入图片描述 Fanout 交换机 Fanout 交换机会将收到的消息路由到每一个跟其绑定的queue上。 我们做一个交换机,两个队列,两个消费者分别连接两个队列。 定义交换…...

数据结构单链表的前插法实现
单链表的前插法实现可以通过以下步骤进行: 创建一个新的节点,并将要插入的元素存储在新节点的数据域中。 将新节点的指针域指向原链表的头节点。 将原链表的头节点指向新节点。 具体代码实现如下所示: class Node:def __init__(self, da…...

Cocos Creator开发学习路线
1.JavaScript与TypeScript程序设计 由于可以跨平台发布,同时要能支持h5的游戏,cocos creator选择了JavaScript与TypeScript来做为它的开发语言,所以我们要先学习JavaScript与TypeScript。TypeScript是基于JavaScript的一个语法糖,运行的时候被编译为JavaScript,所以我们要…...

C语言:IO操作
引言 I/O操作是一切实现的基础。IO即为input &output 标准IO(stdio) FILE类型贯穿始终,FILE是由typedef定义出来的 vii /usr/include/asm-generic/errno-base.h (errno定义的位置) /usr/include/x86_64-linux-gnu/bits/types/struct…...

算法 | 刷题日记
1.递归通常是用栈来实现的 递归在其本质上是通过函数调用栈(Call Stack)来实现的,而不是队列(Queue)。当你调用一个函数时,该函数的局部变量、参数和返回地址会被压入(push)到一个由…...

微信小程序登录接口
微信小程序登录,实现思路分析: 用户触发登录操作:用户在微信小程序中点击“登录”按钮,触发登录流程。调用微信登录接口:小程序端调用微信提供的登录接口(如wx.login),获取临时登录…...
(5):介绍一种排列组合算法)
VBA实战(Excel)(5):介绍一种排列组合算法
1. 需求场景 有多个条件,条件个数不定,每个条件有若干种情况,情况个数不定,输出所有条件可能的情况的排列组合。 2.举例 假设第一次有5个情况要填,第一个条件20种情况,第二个5种,第三个40种&…...

迭代器的使用
参考: 生成器迭代器next函数 迭代器的使用 说到迭代器就必须先要提一下可迭代对象(iterable),可迭代对象是能够逐一返回其成员项的对象。可迭代对象包括序列类型(如list、str、tuple)和非序列类型&#…...

安卓手机APP开发___广播概述
安卓手机APP开发___广播概述 目录 概述 关于系统广播 系统广播所发生的更改 接收广播 清单声明的接收器 上下文注册的接收器 对进程状态的影响 发送广播 通过权限限制广播 带权限的发送 带权限的接收 安全注意事项和最佳做法 概述 Android 应用可以通过 Android …...

【封装】Unity切换场景不销毁物体
在切换场景时,如果物体不需要销毁,可以直接使用下方脚本 代码 public class DontDestroyLoader : MonoBehaviour{ //所有不销毁的物体预制体[SerializeField] private GameObject[] dontDestroyPrefabs;//实例化预制体public void Load(){foreach (var …...

基于学习的决策树
基于学习的决策树概述 决策树是一种监督学习方法,广泛应用于分类和回归任务中。基于学习的决策树模型通过学习数据中的特征来构建树状结构,帮助做出决策。以下是对基于学习的决策树的详细介绍,包括其基本概念、工作流程、构建算法、优势和挑…...

godot.bk2
1.$node_name 其实 就是 get_node 的语法糖 2.场景内部用get_node,场景外部用信号 这是自定义信号的绑定,如果是内置信号,直接右键点击链接到一个函数即可 3.场景切换和摄像头一直居中 4.class_name命名一个类,extends继承&…...

STM32 IIC 使用 HAL 库操作eeprom
在STM32上通过I2C接口(注意:在标准STM32库中,I2C接口通常被写为"I2C"而不是"IIC")与EEPROM芯片通信时,你需要遵循I2C通信协议,并使用STM32的HAL库或标准外设库(如果适用&am…...
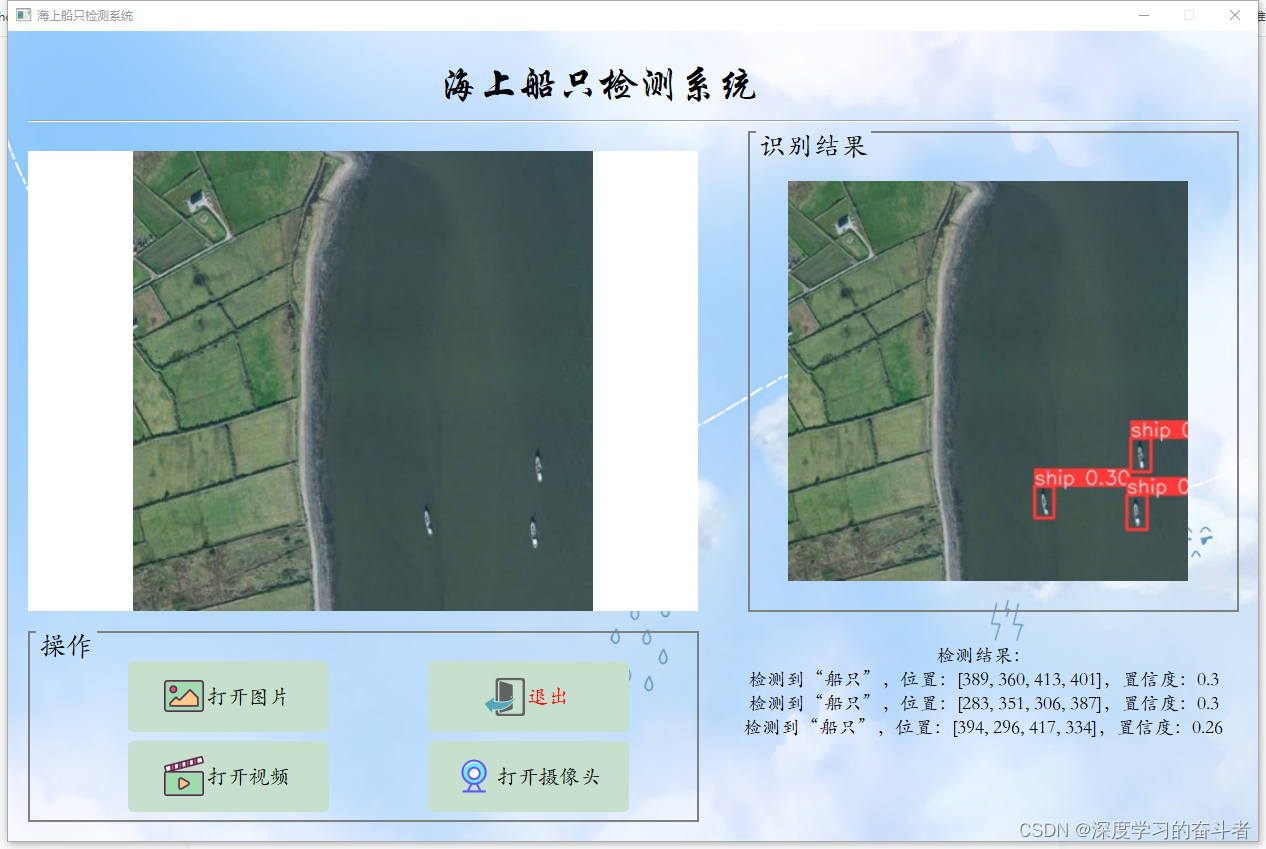
YOLOv8+PyQt5海洋船只检测(可以重新训练,yolov8模型,从图像、视频和摄像头三种路径识别检测)
1.效果视频:海洋船只检测yoloV8检测(https://mbd.pub/o/bread/mbd-ZpaYk55r)_哔哩哔哩_bilibili资源包含可视化的海洋船只检测系统,可对于高空拍摄到的海洋图片进行轮船检测,基于最新的YOLOv8训练的海洋船只检测模型&a…...

PCL 高阶多项式曲线回归拟合(二维)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 高阶多项式曲线回归(Polynomial Regression)是一种线性回归模型的扩展,它允许数据拟合一个非线性的曲线。虽然多项式本身是非线性的,但我们可以通过引入新的变量(例如,原始变量的平方、立方等)来将问题转化为…...

深入理解 Python3 函数:从基础语法到高级应用
Python3 函数是构建模块化代码的基本单位,允许我们将代码组织成独立的、可重用的块。本文将详细介绍 Python3 函数的基本语法、常用命令、示例、应用场景、注意事项,并进行总结。 基本语法 在 Python 中,函数的定义使用 def 关键字…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
