16-云原生监控体系-rabbitmq_exporter监控 RabbitMQ-[部署Dashborad告警规则实战]
文章目录
- 1. 二进制方式部署
- 1.1. 二进制包下载和部署
- 1.2. 配置
- 1.2.1. 可用的环境变量
- 1.2.2. 使用变量
- 2. docker-compose 方式部署
- 3. 配置到 Prometheus
- 3. Metrics
- 3.1. 全局
- 3.2. 基础信息
- 3.3. Queues
- 3.3.1 Queues - Gauge
- 3.3.2. Queues - Counter
相关文章:

16-云原生监控体系-rabbitmq_exporter监控 RabbitMQ-[部署Dashborad告警规则实战]
文章目录 1. 二进制方式部署1.1. 二进制包下载和部署1.2. 配置1.2.1. 可用的环境变量1.2.2. 使用变量2. docker-compose 方式部署3. 配置到 Prometheus3. Metrics3.1. 全局3.2. 基础信息3.3. Queues3.3.1 Queues - Gauge3.3.2. Queues - Counter...

四大运营商频段-2024
四大运营商频段-2023 中国移动900MHz(Band8),889-904/934-949MHz:1.8GHz(Band3),1710-1735/1805-1830MHz:1.9GHz(Band39),1885-1915MHz:2GHz(Band34),2010-2025MHz:2.3GHz(Band40),2320-2370MHz:2.6GHz(Band41,n41),25…...

260只出现一次的数字
一:题目描述 二:思路讲解 三:代码 class Solution { public:vector<int> singleNumber(vector<int>& nums) {int sum 0;for(const int& e : nums){sum ^ e;}int l (sum INT_MIN ? sum : sum&(-sum));int sum1 0…...

【高阶数据结构(八)】跳表详解
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:高阶数据结构专栏⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习更多数据结构 🔝🔝 高阶数据结构 1. 前言2. 跳表的概…...

用旧安卓手机当 linux 开发机
1. 下载 Termux (快速链接,如果失效或者要下载最新版请去github release 下载 ) 注意手机硬件,我这个是 64 的所以下 64 的 https://github.com/termux/termux-app/releases/download/v0.118.0/termux-app_v0.118.0github-debug_arm64-v8a.apk 2. 弄到…...
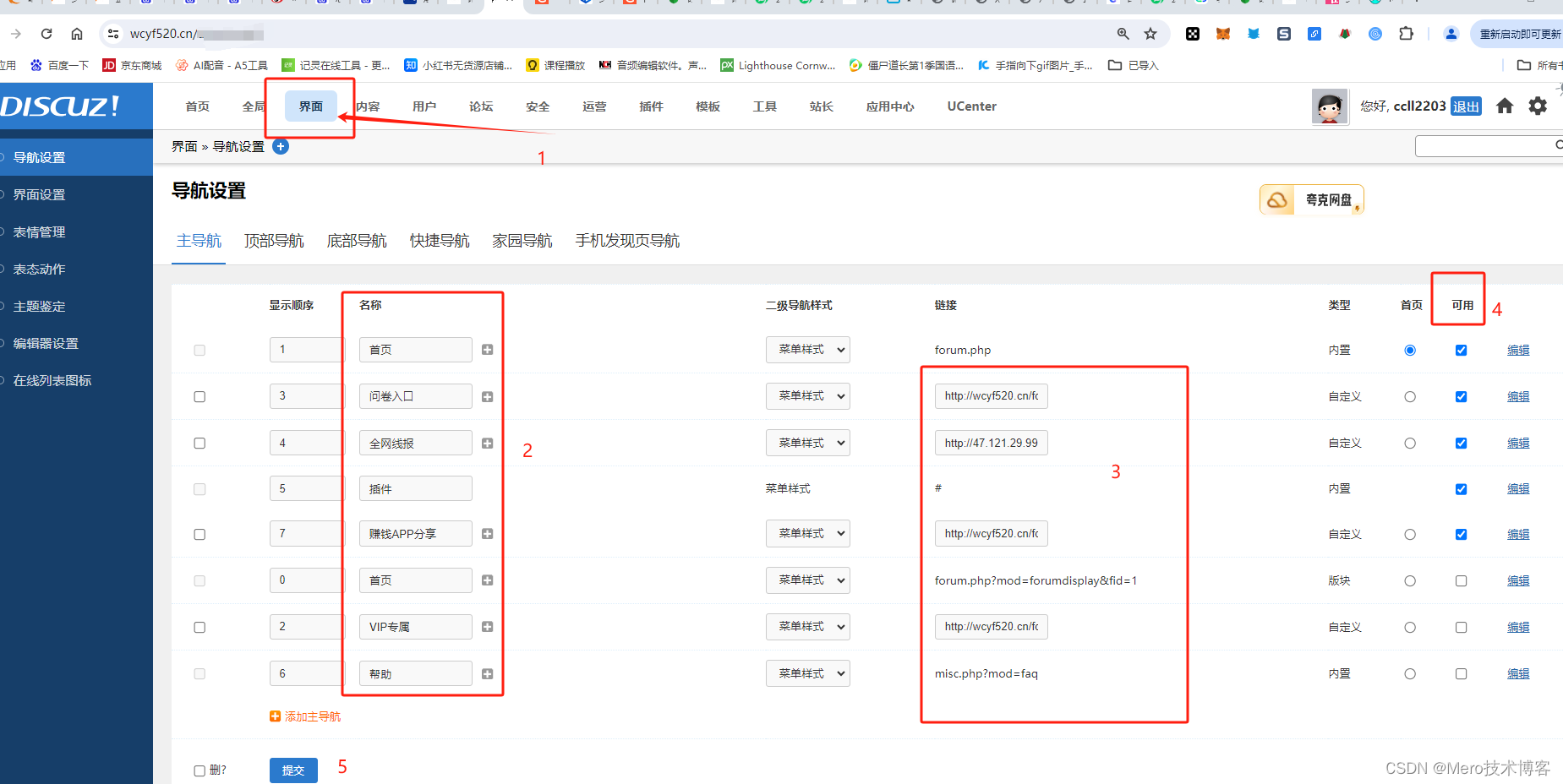
discuz如何添加主导航
大家好,今天教大家怎么样给discuz添加主导航。方法其实很简单,大家跟着我操作既可。一个网站的导航栏是非常重要的,一般用户进入网站的第一印象就是看网站的导航栏。如果大家想看效果的话可以搜索下网创有方,或者直接点击查看效果…...

[每日一练]患某种疾病的患者,正则表达式的匹配
该题目来源于力扣: 1527. 患某种疾病的患者 - 力扣(LeetCode) 题目要求: 患者信息表: Patients ----------------------- | Column Name | Type | ----------------------- | patient_id | int | | pati…...

PHP身份证识别接口、线上平台如何实现身份证实名认证功能?
线上平台实现身份证实名认证的功能,需要结合身份证识别接口来完成。首先,用户通过上传身份证图片或者拍照的方式实现证件信息的提取,身份证实名认证接口通过对提取到的证件信息进行核验,以此来实现线上用户身份的实名认证…...
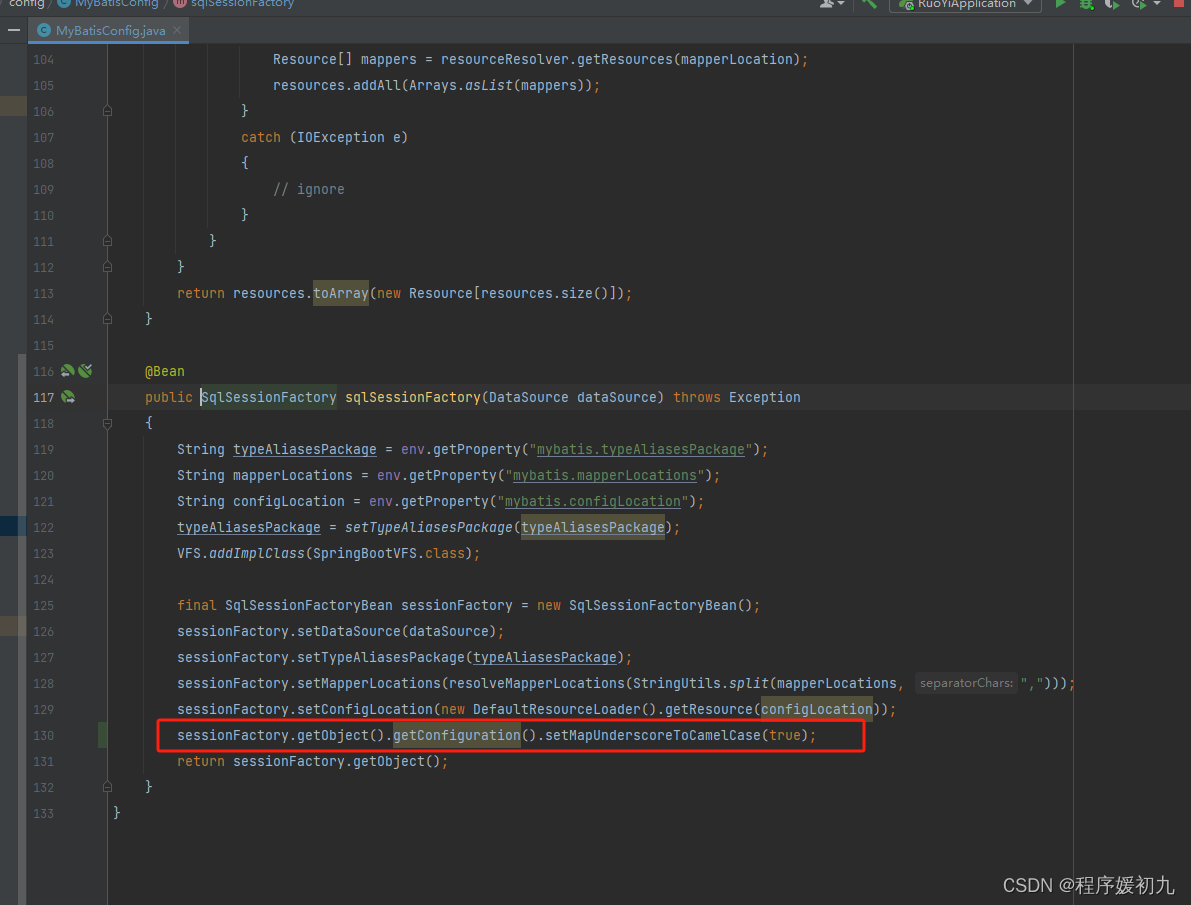
若依:mybatis查询的结果未映射到实体类报null
开启驼峰命名转换: mapUnderscoreToCamelCase: true 我的是mtybatis配置开启驼峰命名转换不生效,还需要在MyBatisConfig中配置 // 配置mybatis自动转驼峰 生效 sessionFactory.getObject().getConfiguration().setMapUnderscoreToCamelCase(true)&#x…...

成都百洲文化传媒有限公司电商服务可信吗?
在当今数字化浪潮席卷之下,电商行业蓬勃发展,成为推动经济增长的重要引擎。在这一领域,成都百洲文化传媒有限公司凭借其专业的电商服务,迅速崛起,成为行业的佼佼者。该公司不仅深谙电商市场的运营之道,更以…...
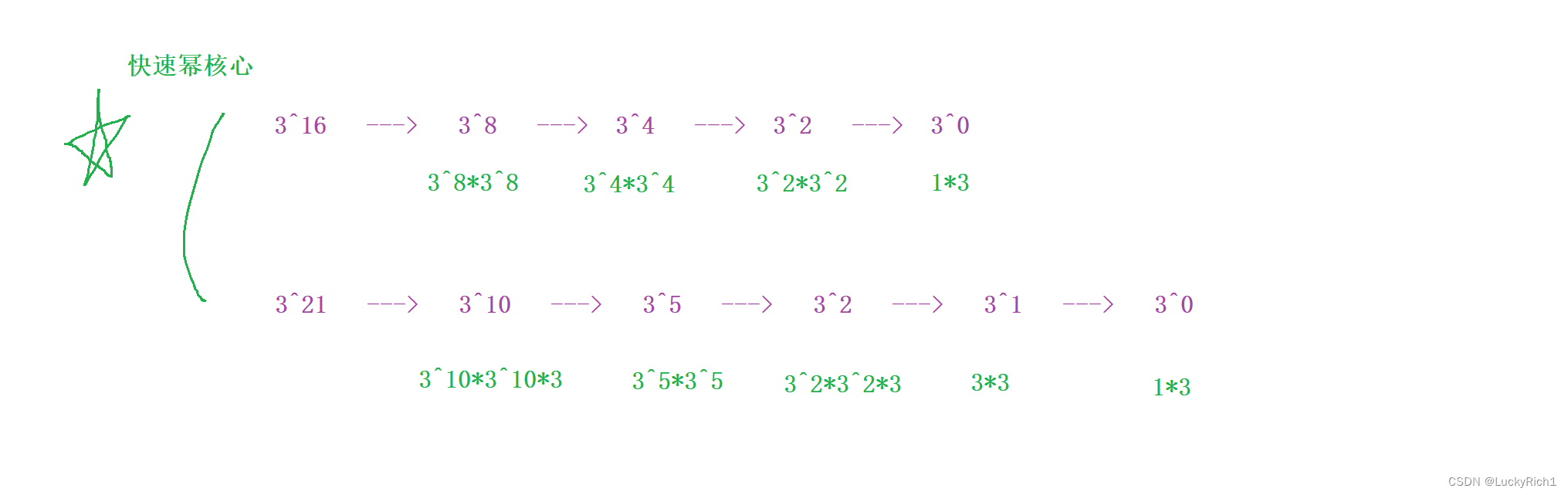
【递归、搜索与回溯】递归、搜索与回溯准备+递归主题
递归、搜索与回溯准备递归主题 1.递归2.搜索3.回溯与剪枝4.汉诺塔问题5.合并两个有序链表6.反转链表7.两两交换链表中的节点8.Pow(x, n)-快速幂(medium) 点赞👍👍收藏🌟🌟关注💖💖 你…...

MVC前端怎么写:深入解析与实战指南
MVC前端怎么写:深入解析与实战指南 在Web开发领域,MVC(Model-View-Controller)是一种广泛使用的架构模式,它将应用程序的数据、界面和控制逻辑分离,使得代码更加清晰、易于维护。本文将详细探讨MVC前端如何…...

LINUX网络设置
一、1.1.ifconfig:当前设备正在启动的网卡(启动的) ifconfig -a :当前所有设备的网卡(启动的和没有启动的都包括) 1.2.ifconfig展示的ens33各行含意: 1.2.1 ens33: flags 4163<UP, …...

双指针解题
验证回文数(验证回文数-CSDN博客)和判断在子序列(判断子序列-CSDN博客)已经在之前进行了计算,今天有三个新的双指针问题: 两数之和II—输入有序数组 给你一个下标从 1 开始的整数数组 numbers ࿰…...
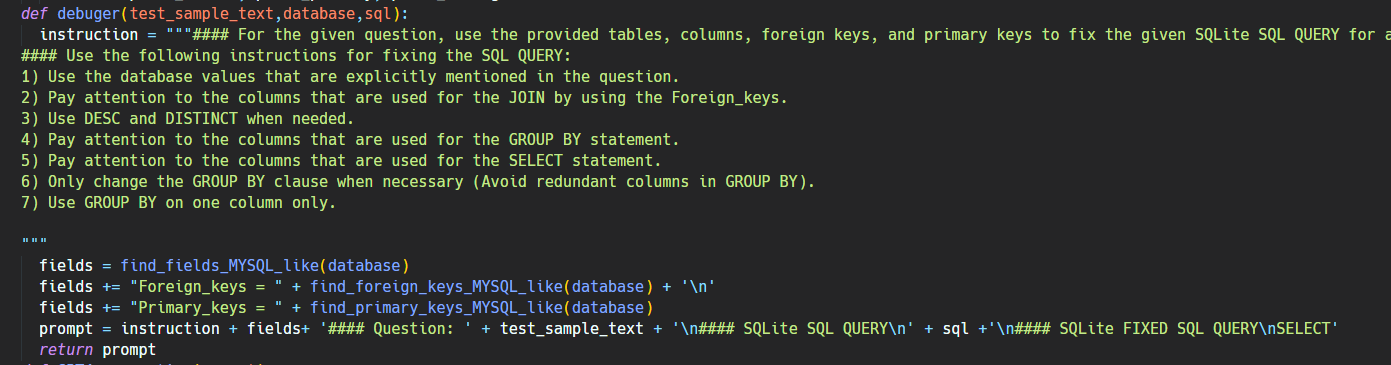
【Text2SQL 论文】DIN-SQL:分解任务 + 自我纠正 + in-context 让 LLM 完成 Text2SQL
论文:DIN-SQL: Decomposed In-Context Learning of Text-to-SQL with Self-Correction ⭐⭐⭐⭐ NeurIPS 2023, arXiv:2304.11015 Code: Few-shot-NL2SQL-with-prompting | GitHub 文章目录 一、论文速读1.1 Schema Linking Module1.2 Classification & Decompo…...

基于Springboot+vue实现的汽车服务管理系统
作者主页:Java码库 主营内容:SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、安卓app等设计与开发。 收藏点赞不迷路 关注作者有好处 文末获取源码 技术选型 【后端】:Java 【框架】:spring…...

ROS2从入门到精通4-3:全局路径规划插件开发案例(以A*算法为例)
目录 0 专栏介绍1 路径规划插件的意义2 全局规划插件编写模板2.1 构造规划插件类2.2 注册并导出插件2.3 编译与使用插件 3 全局规划插件开发案例(A*算法)常见问题 0 专栏介绍 本专栏旨在通过对ROS2的系统学习,掌握ROS2底层基本分布式原理,并具有机器人建…...
Java学习【认识异常】
Java学习【认识异常】 认识异常异常的种类异常的作用 异常的处理方式JVM默认的处理方式捕获异常finally 多个异常的处理异常中的方法抛出异常 自定义异常 认识异常 在Java中,将程序执行过程中发生的不正常行为称为异常 异常的种类 Error代表的是系统级别的错误&a…...

uniapp+h5 ——微信小程序页面截屏保存在手机
web-view 需要用到 web-view ,类似于iframe, 将网页嵌套到微信小程序中,参数传递等; 示例(无法实时传递数据),页面销毁时才能拿到h5传递的数据,只能利用这点点击跳转到小程序另一个…...
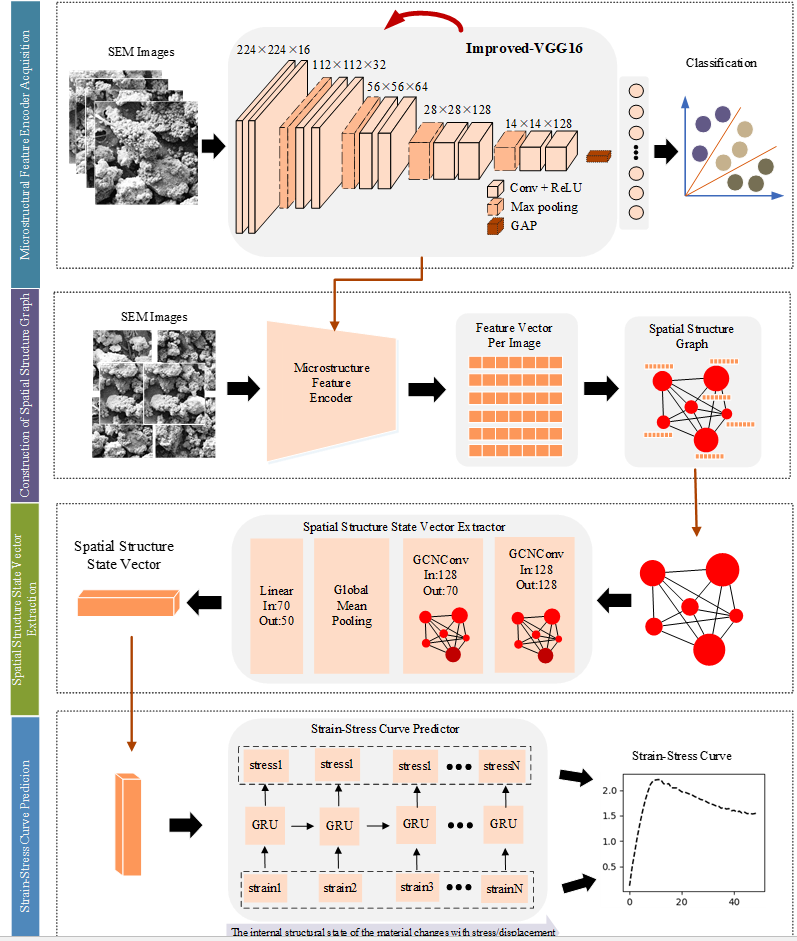
三、基于图像分类预训练编码及图神经网络的预测模型 【框图+源码】
背景: 抽时间补充,先挖个坑。 一、模型结构 二、源码...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
