GEE案例——归一化差异水体指数丰水期、枯水期的水域面积和水深分析(青海湖为例)
简介
水深反演是指利用遥感技术从航空或卫星平台上获取的数据来推断水体的深度信息。这种技术在海洋学、湖泊和河流的科学研究与管理中非常重要。以下是几种常用的水深反演方法:
1. **光学遥感反演**:
- 基于水体颜色和透明度的变化与水深的关系,使用光学遥感影像(如Landsat、Sentinel等)进行水深估算。
- 通常适用于清澈的浅水环境,因为水体的光学特性会随着深度的增加而变化。
2. **多光谱和高光谱遥感**:
- 利用水体对不同波长光的吸收和散射特性,通过分析多光谱或高光谱数据来估算水深。
3. **激光雷达(LiDAR)**:
- 通过发射激光脉冲并接收从水体表面反射回来的光来测量水深。
- LiDAR技术能够提供高精度的水深数据,尤其适用于沿海和河岸区域。
4. **合成孔径雷达(SAR)**:
- SAR技术可以用于观测水体表面的粗糙度和波动,这些特性与水深有关。
- 特别适用于海洋和大面积水体的水深反演。
5. **差分GPS(DGPS)**:
- 结合差分GPS和声学测量技术,可以提高水深测量的精度。
6. **声学方法**:
- 使用声纳(侧扫声纳、回声声纳)发射声波并接收从水底反射的声波,通过声波的传播时间来计算水深。
- 是一种传统的水深测量方法,适用于各种水深条件。
7. **遥感数据与地面测量结合**:
- 结合遥感数据和地面实测数据,通过经验模型或机器学习算法来提高水深反演的精度。
8. **遥感数据融合**ÿ
相关文章:
)
GEE案例——归一化差异水体指数丰水期、枯水期的水域面积和水深分析(青海湖为例)
简介 水深反演是指利用遥感技术从航空或卫星平台上获取的数据来推断水体的深度信息。这种技术在海洋学、湖泊和河流的科学研究与管理中非常重要。以下是几种常用的水深反演方法: 1. **光学遥感反演**: - 基于水体颜色和透明度的变化与水深的关系,使用光学遥感影像(如L…...

机器视觉检测--相机
一,相机就是CCD么? 通常,我们把相机都叫作CCD,CCD已经成了相机的代名词。其实很可能正在使用的是CMOS。CCD以及CMOS都称为感光元件,都是将光学图像转换为电子信号的半导体元件。他们在检测光时都采用光电二极管&#…...

【人工智能】第四部分:ChatGPT的技术实现
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...

小程序配置自定义tabBar及异形tabBar配置操作
什么是tabBar? 小程序的tabbar是指小程序底部的一组固定导航按钮,通常包含2-5个按钮,用于快速切换小程序的不同页面。每个按钮都有一个图标和文本标签,点击按钮可以切换到对应的页面。tabbar通常放置在小程序的底部,以…...

解析《动物园规则怪谈》【逻辑】
鉴赏《动物园规则怪谈》【逻辑】 前言版权推荐鉴赏《动物园规则怪谈》推理游客正方“它”方其他物品 不同规则或纸条的对比联系出现的地方及联系游客入园历程:被“它”污染的过程鉴赏升华 最后 前言 2024-5-31 13:05:38 以下内容源自《【逻辑】》 仅供学习交流使用…...
上传RKP 证书签名请求息上传到 Google 的后端服务器
上传证书签名请求 1.准备环境:OK pip3 install google-auth2.13.0 requests2.28下载 device_info_uploader.py 。 没找到先跳过 选项 1:通过 GCP 帐户使用 device_info_uploader.py 运行脚本。 ./device_info_uploader.py --credentials /secure/s…...

Debian和ubuntu 嵌入式的系统的 区别
随着开源操作系统的日益流行,Debian和Ubuntu这两个基于Linux的发行版本成为了众多开发者和系统管理员的首选。它们各自拥有独特的优势和特点,那么,在选择时,哪一个更适合你呢?接下来,我们将深入探讨两者的关…...

HTML旋转照片盒子
效果图 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><meta http-equiv"X-UA-Compatible" content…...
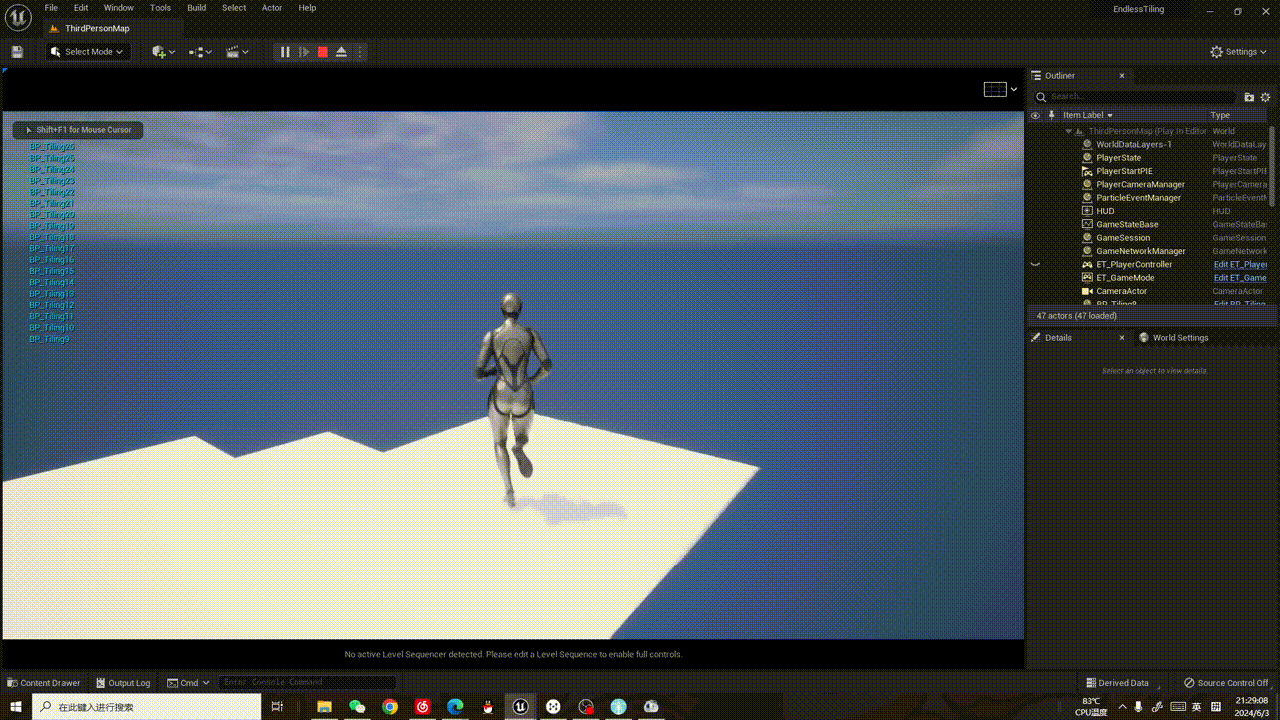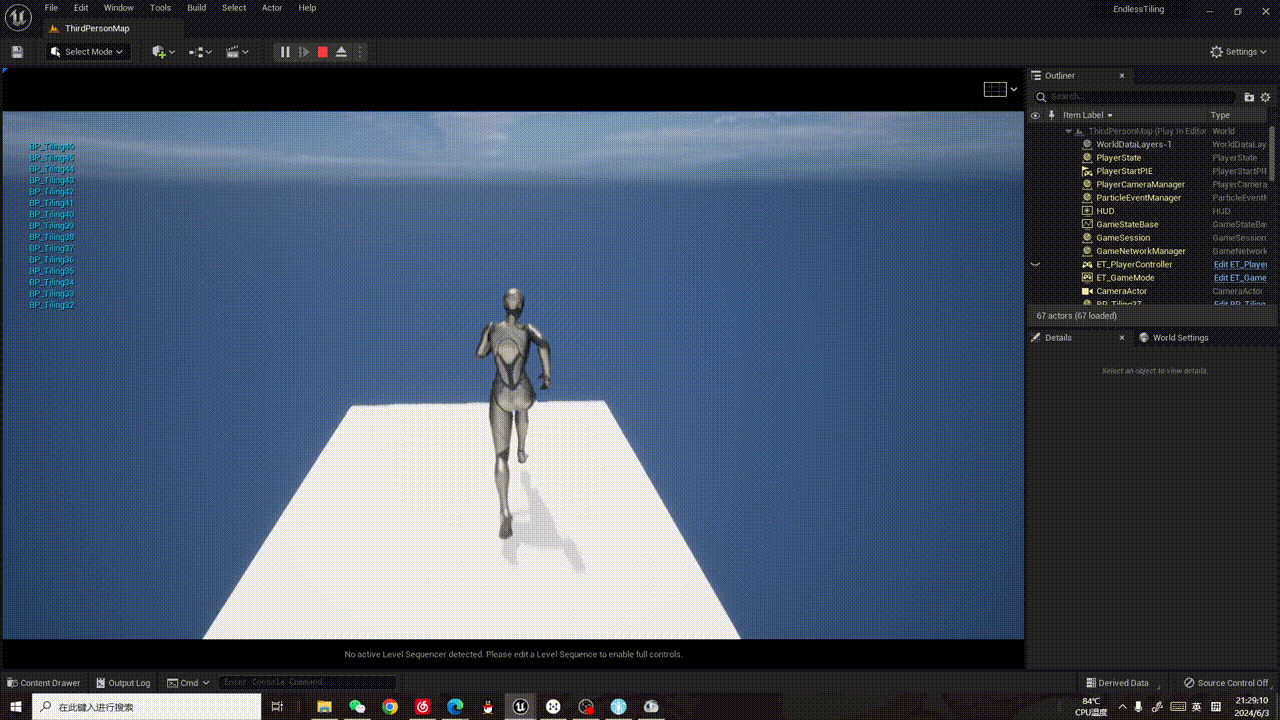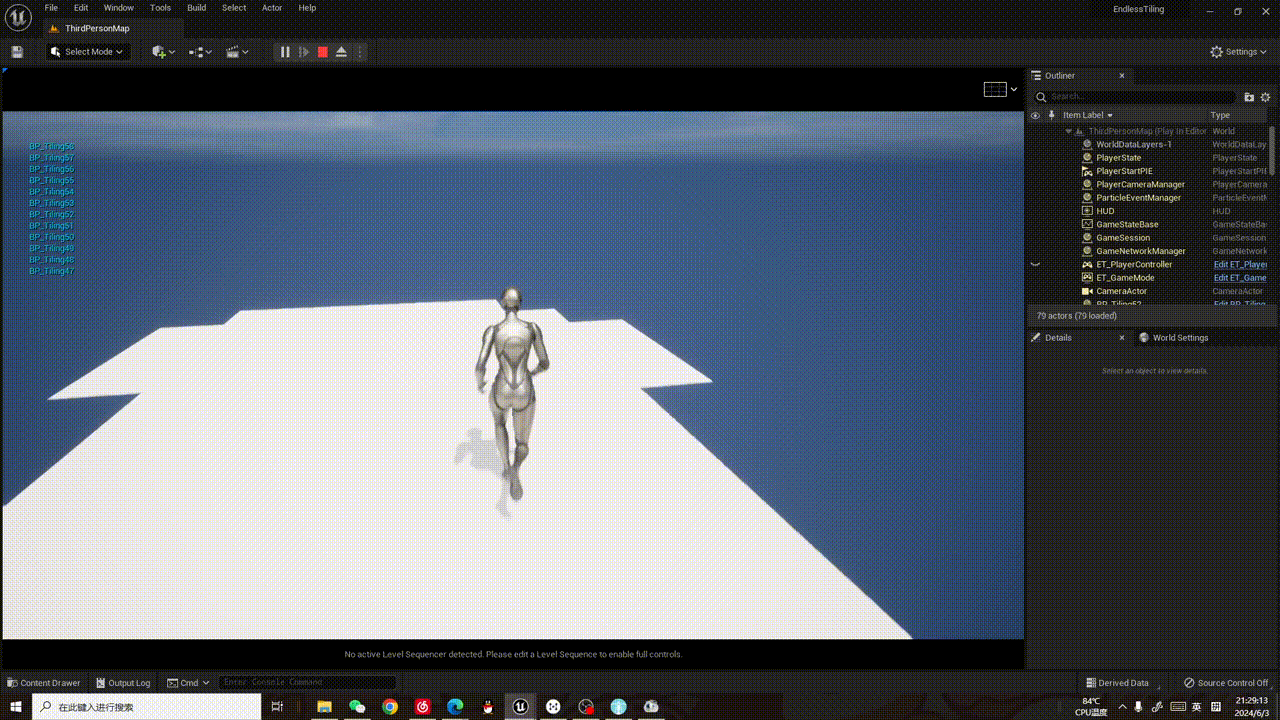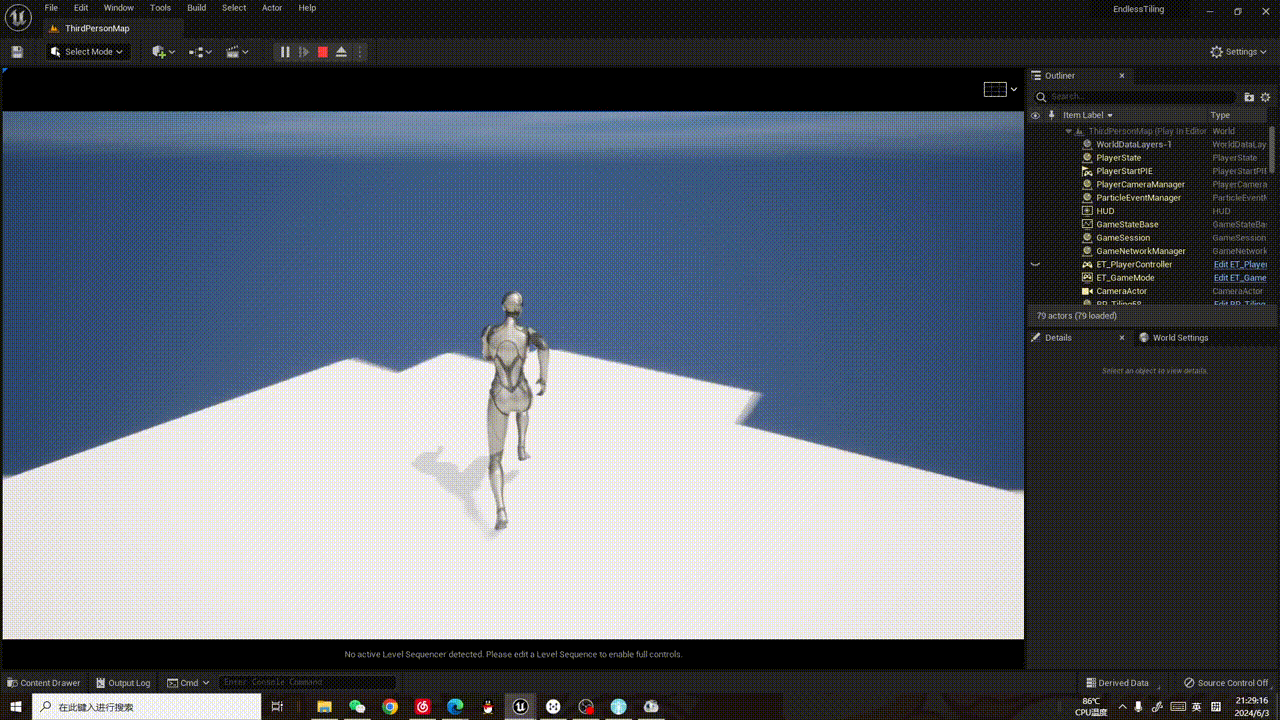
【UE5 刺客信条动态地面复刻】实现无界地面01:动态生成
2024.6.4更新 昨天半夜意识到生成Cube的方案不合适,又开始到处找动态地面的方法,发现了我想要的效果直接可以用nigara实现!!!! 于是这个部分就暂时告一段落,今季开始新的方向的学习。 为了快速…...

AI产品经理系列-如何使用kimi快速撰写用户故事(含提示词)
在AI时代,可能人人都可成为产品经理。 之前我们聊过如何使用kimi协助完成产品需求文档,如何写竞品分析报告,这一篇我们聊聊用户故事,如何使用kimi协助撰写产品需求文档中的用户故事。 在此之前我们先了解下什么是用户故事&#…...
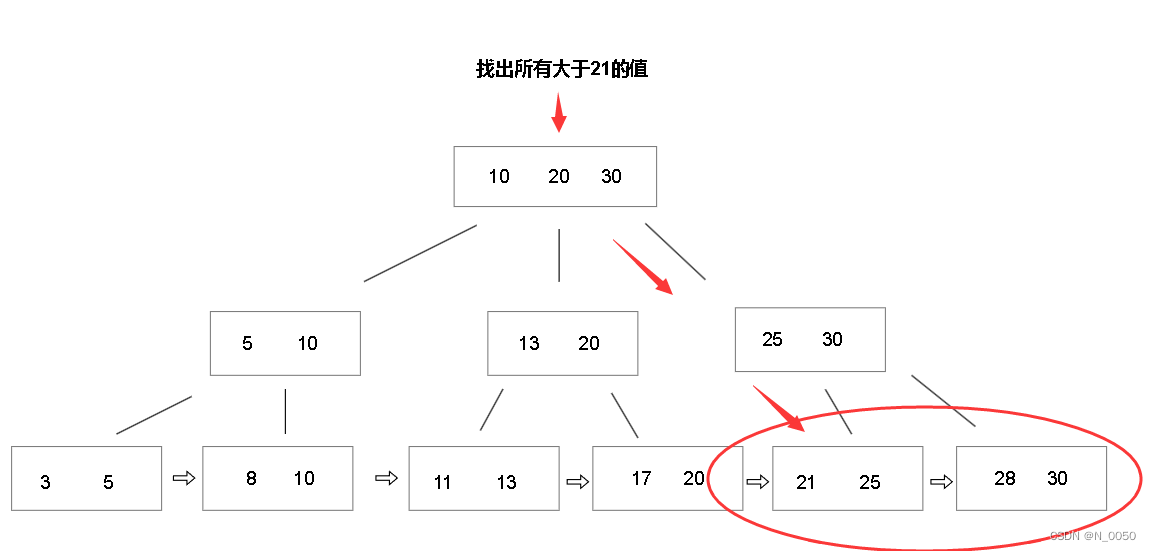
MySQL索引与事务
前言👀~ 紧接着数据库的相关知识,今天讲解MySQL面试中频繁被问到的知识点,索引与事务!!! 如果各位对文章的内容感兴趣的话,请点点小赞,关注一手不迷路,如果内容有什么问题的话,欢迎各位评论纠正…...

『大模型笔记』从基础原理出发提升深度学习性能
从基础原理出发提升深度学习性能 文章目录 一. 从基础原理出发提升深度学习性能1.1. 计算(compute)1.2. 带宽(Bandwidth)1.2.1 关于内存带宽成本的推理(Reasoning about Memory-Bandwidth Costs)1.3. 开销(Overhead)二. 总结三. 参考文献Making Deep Learning Go Brrrr F…...
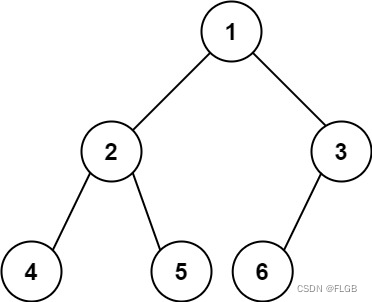
【二叉树】Leetcode 222. 完全二叉树的节点个数【简单】
完全二叉树的节点个数 你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。 完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最…...

golang界面设计器,全网少见
今天登录govcl的网站,无意中看到有个简易UI设计器。 对于golang的UI专用设计器,还没在网上真正见过。 之前也用govcl来做过两三个桌面应用,好用是好用,不过要安装Lazarus的IDE来拖动设计UI,还要配置很多东西࿰…...
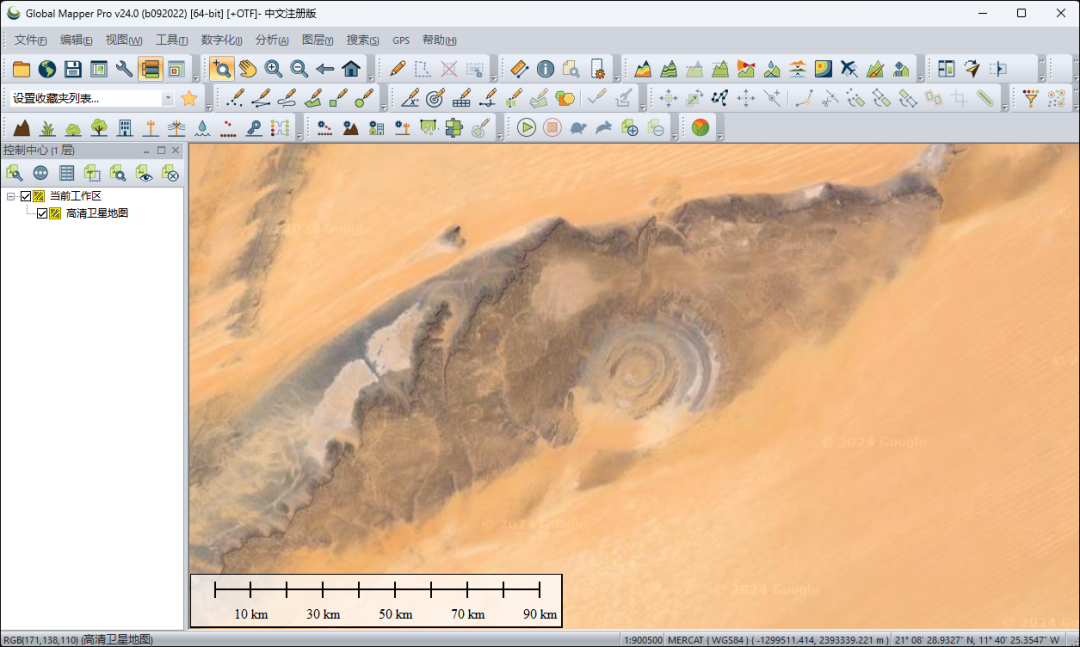
如何在GlobalMapper中加载高清卫星影像?
GlobalMapper在GIS行业几乎无人不知,无人不晓,但它可以直接加载卫星影像也许就不是每个人都知道的了。 这里就来分享一下如何在GlobalMapper中加载高清卫星影像,并可以在文末查看领取软件安装包和图源的方法。 如何加载高清图源 首先&…...

【机器学习】解锁AI密码:神经网络算法详解与前沿探索
👀传送门👀 🔍引言🍀神经网络的基本原理🚀神经网络的结构📕神经网络的训练过程🚆神经网络的应用实例💖未来发展趋势💖结语 🔍引言 随着人工智能技术的飞速发…...
Java如何实现pdf转base64以及怎么反转?
问题需求 今天在做发送邮件功能的时候,发现邮件的附件部分,比如pdf文档,要求先把pdf转为base64,邮件才会发送。那接下来就先看看Java 如何把 pdf文档转为base64。 两种方式,一种是通过插件 jar 包的方式引入…...

动态规划5:62. 不同路径
动态规划解题步骤: 1.确定状态表示:dp[i]是什么 2.确定状态转移方程:dp[i]等于什么 3.初始化:确保状态转移方程不越界 4.确定填表顺序:根据状态转移方程即可确定填表顺序 5.确定返回值 题目链接:62. …...
-列表(List))
Python编程学习第一篇——Python零基础快速入门(五)-列表(List)
今天我们来一起学习Python的列表(list),Python中的列表(List)是一种有序、可变的数据结构,可以用来存储多个值。列表可以包含不同类型的数据,例如整数、浮点数、字符串等。以下是关于Python列表…...

c# - 运算符 << 不能应用于 long 和 long 类型的操作数
Compiler Error CS0019 c# - 运算符 << 不能应用于 long 和 long 类型的操作数 处理方法 特此记录 anlog 2024年5月30日...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...
