力扣----轮转数组
题目链接:189. 轮转数组 - 力扣(LeetCode)

思路一
我们可以在进行每次轮转的时候,先将数组的最后一个数据的值存储起来,接着将数组中前n-1个数据依次向后移,最后将存储起来的值赋给数组中的第一个数据。
先将数组中最后的一个元素的值存到变量tmp中,如下图
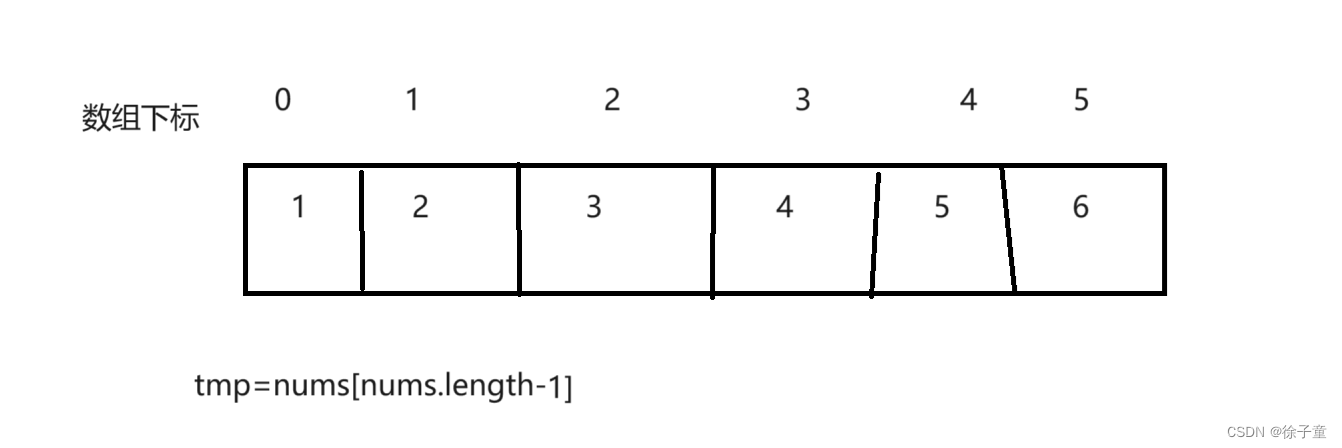
接着将数组中前n-1个数据依次向后移,如下图
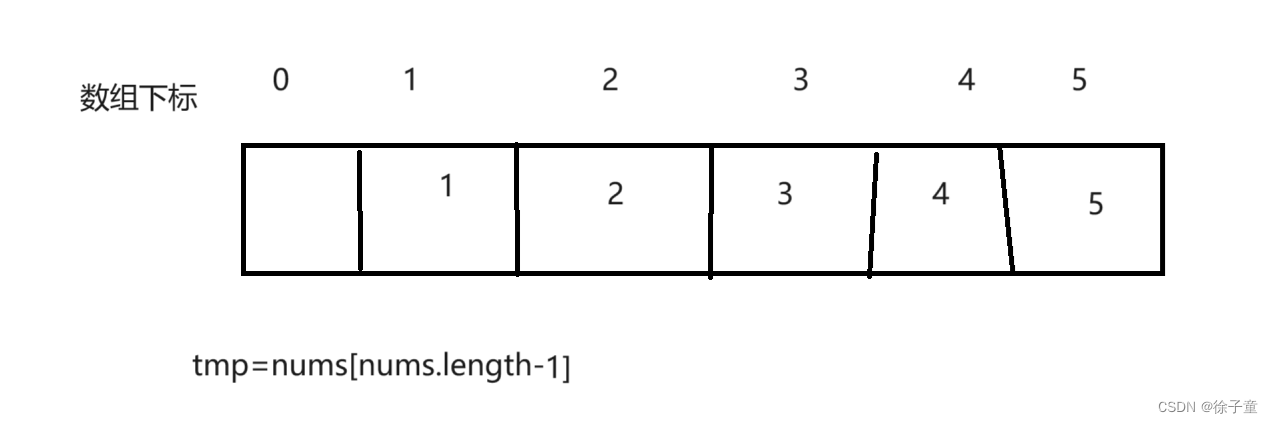
最后再将tmp中的值赋值给nums[0],如下图
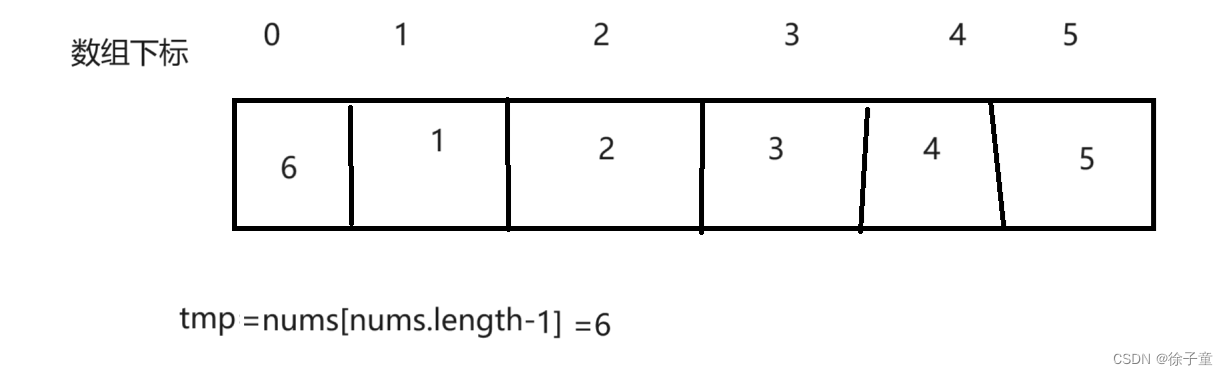
以上图是表示一次轮转的,如果还要轮转,重复上面的操作。
代码实现
public void rotate(int[] nums, int k) {for(int i=0;i<k;i++){int tmp=nums[nums.length-1];//将前n-1个元素向后移for(int j=nums.length-1;j>0;j--){nums[j]=nums[j-1];}nums[0]=tmp;}}当我们提交以上代码时,会发现不成功。
思路是对的,但是上面代码时间复杂度为O(kn),太复杂了,超出了题目的时间限制。
思路二
造成思路一时间复杂度太大的原因是: 思路一中有两个循环,一个循环是数组右旋的次数,另一个循环要将数组中的元素全部遍历一遍,这样当右旋次数足够多,数组中的元素很多时,效率就很低了。
思路二是k次旋转法。
下面以旋转次数为3来讲解,也就是k=3
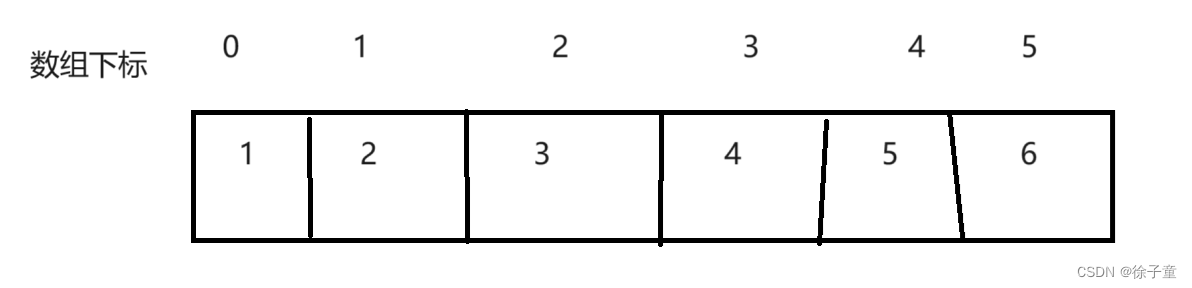
先将数组全部旋转一遍,如下图
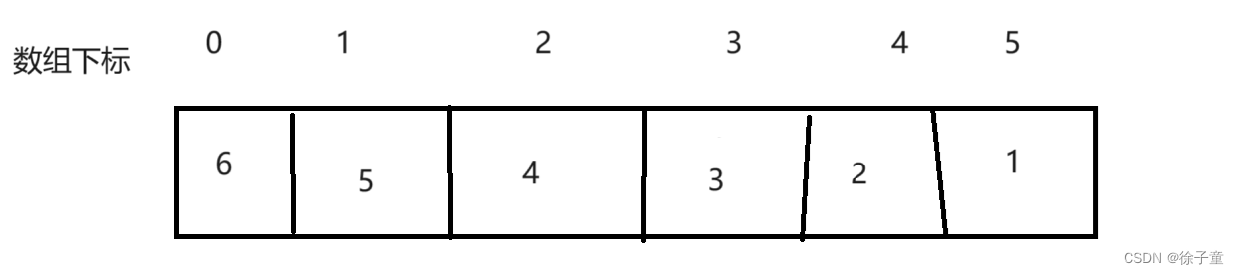
再以下标为0为起始点和下标为(k%nums.length)-1为终点来旋转,如下图
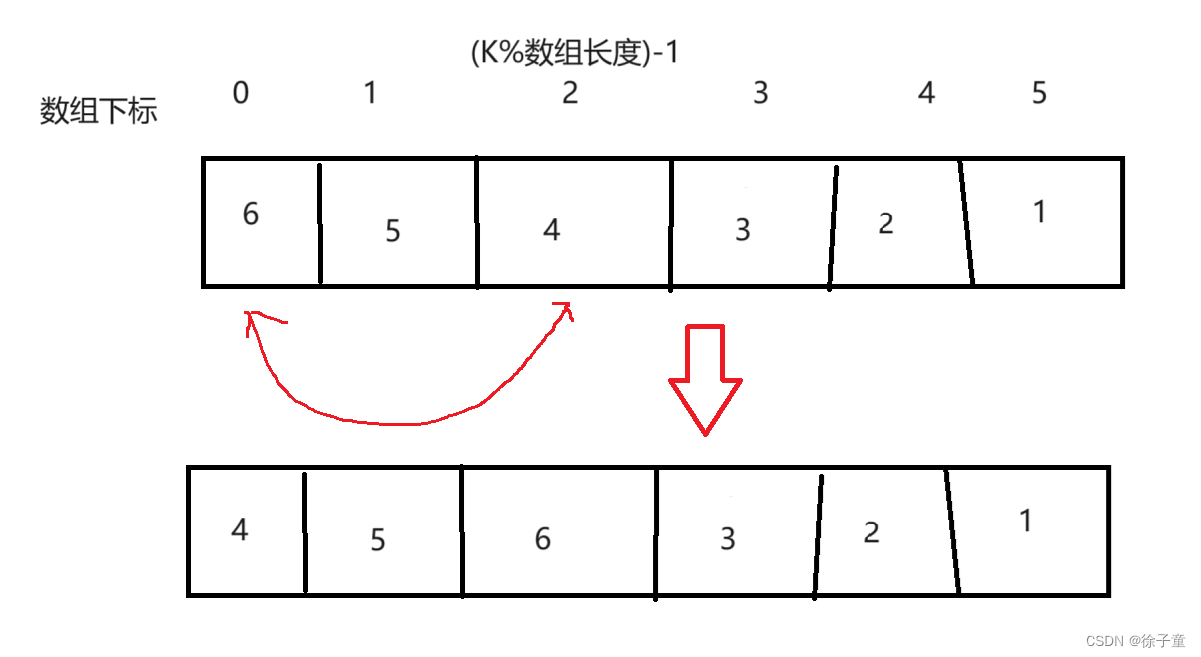
最后以下标为(K%数组长度)为起始点和以下标为(数组长度-1)为终点来旋转数组。
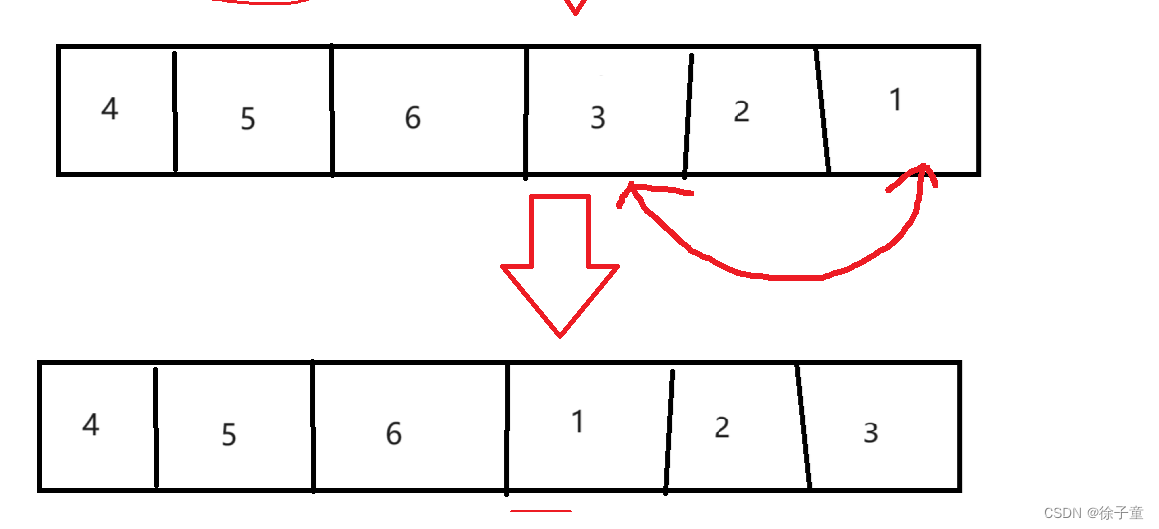
这样就完成了数组的3次右旋。
代码实现
public void reverse(int[] nums,int start,int end){while(start<end){int tmp=nums[start];nums[start]=nums[end];nums[end]=tmp;start++;end--;}}public void rotate(int[] nums, int k) {reverse(nums,0,nums.length-1);reverse(nums,0,(k%nums.length)-1);reverse(nums,k%nums.length,nums.length-1);}思路三
我们可以创建一个新的数组,将原数组中的数据按照数组旋转之后的的位置放置到新数组中对应的位置。最后我们再将新数组复制到原数组中就行了。
有一个公式:((i+k)%数组的长度) 的值 是 原数组中下标为i的数据 在 新数组中的位置。
其中i为原数组中数据的小标,k为旋转次数。
理解公式:
假如数组向右旋转k,也就是让数组中的数据向右移动k个位置,但是如果k大于数组长度,就会越界,所以我们要%数组的长度。因为如果旋转的次数超过数组的长度,也就是旋转k次的效果和k减去数组的长度次的效果是一样的。
代码实现
public void rotate(int[] nums, int k) {int n=nums.length;//创建一个新数组jianint[] newNums=new int[n];//将原数组中的数据放到新数组中for(int i=0;i<n;i++){newNums[(i+k)%n]=nums[i];}//将新数组复制到原数组System.arraycopy(newNums,0,nums,0,n);}相关文章:

力扣----轮转数组
题目链接:189. 轮转数组 - 力扣(LeetCode) 思路一 我们可以在进行每次轮转的时候,先将数组的最后一个数据的值存储起来,接着将数组中前n-1个数据依次向后移,最后将存储起来的值赋给数组中的第一个数据。 …...

哥斯拉、冰蝎、中国蚁剑在护网中流量特征分析,收藏起来当资料吧,24年护网用得上
护网哥斯拉、冰蝎、中国蚁剑流量分析 【点击免费领取】CSDN大礼包:《黑客&网络安全入门&进阶学习资源包》🔗包含了应急响应工具、入侵排查、日志分析、权限维持、Windows应急实战、Linux应急实战、Web应急实战。 护网中最担心的是木马已经到了服…...

隐藏饼图的legend,重写legend列表。
因为要实现的饼图效果较复杂,所以,需要重新写列表。 点击右侧列表的圆点,实现隐藏左侧饼图相应环状。 <template><div class="index_div"><a-spin :spinning="aLoading"><scalescreen:width="1920":height="1080&…...

解决在Mac下使用npm报错:Error: EACCES: permission denied
原因说明:没有足够的权限在 /usr/local/lib/node_modules 目录下创建文件夹 这个错误表明你在安装或更新 Vue.js(vue)包时,没有足够的权限在 /usr/local/lib/node_modules 目录下创建文件夹。这通常是因为默认情况下,普…...

pvt对net delay的影响
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧? 拾陆楼知识星球入口 有星球成员提问: pt中在同一个corner下的net的为啥在min和max的情况下读RC值是不一样的呢??不应该都是根据spef来的吗?? 回答: 这个其实是个误区,相同RC corner情况下我们看report_delay_…...

力扣5 最长回文子串
给你一个字符串 s,找到 s 中最长的 回文子串。 示例 1: 输入:s "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。示例 2: 输入:s "cbbd" 输…...

【Uniapp小程序】自定义导航栏uni-nav-bar滚动渐变色
效果图 新建activityScrollTop.js作为mixins export default {data() {return {navBgColor: "rgba(0,0,0,0)", // 初始背景颜色为完全透明navTextColor: "rgba(0,0,0,1)", // 初始文字颜色};},onPageScroll(e) {// 设置背景const newAlpha Math.min((e.s…...
HarmonyOS鸿蒙学习笔记(25)相对布局 RelativeContainer详细说明
RelativeContainer 简介 前言核心概念官方实例官方实例改造蓝色方块改造center 属性说明参考资料 前言 RelativeContainer是鸿蒙的相对布局组件,它的布局很灵活,可以很方便的控制各个子UI 组件的相对位置,其布局理念有点类似于android的约束…...

自然语言处理学习中英文翻译语料库
在自然语言处理(NLP)领域,学习中英文翻译需要高质量的双语语料库。以下是一些常用的中英文翻译语料库资源: OpenSubtitles: 网站: OpenSubtitles 描述:OpenSubtitles 提供了大量的电影和电视剧…...

可视化数据科学平台在信贷领域应用系列二:数据清洗
上一篇文章中,某互联网银行零售信贷风险建模专家使用数据科学平台Altair RapidMiner——完成了数据探索工作,《可视化数据科学平台在信贷领域应用系列一:数据探索》。本次这位建模专家再次和大家分享数据准备的第二步骤,数据清洗。…...
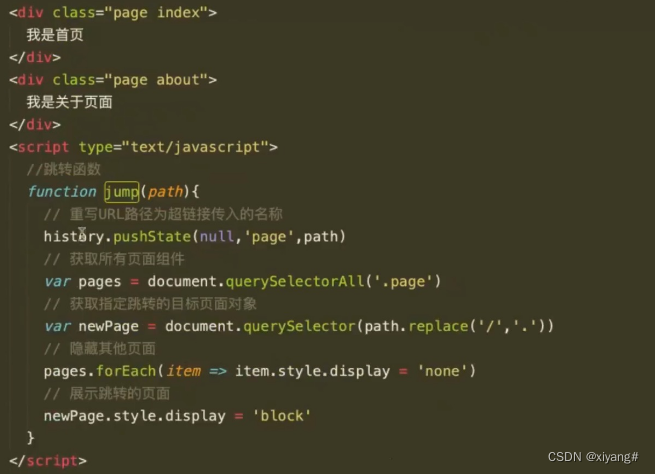
JS面试题:hash和history的区别
一、hash 模式和 history 模式的介绍 由于 Vue 项目为单页面应用,所以整个项目在开发和构建过程中,仅存在一个HTML物理文件。通过路由系统可以实现将项目的组件与可访问的URL路径进行绑定。由于Vue项目只有一个HTML物理文件,切换页面时既需要…...
)
GEE案例——归一化差异水体指数丰水期、枯水期的水域面积和水深分析(青海湖为例)
简介 水深反演是指利用遥感技术从航空或卫星平台上获取的数据来推断水体的深度信息。这种技术在海洋学、湖泊和河流的科学研究与管理中非常重要。以下是几种常用的水深反演方法: 1. **光学遥感反演**: - 基于水体颜色和透明度的变化与水深的关系,使用光学遥感影像(如L…...

机器视觉检测--相机
一,相机就是CCD么? 通常,我们把相机都叫作CCD,CCD已经成了相机的代名词。其实很可能正在使用的是CMOS。CCD以及CMOS都称为感光元件,都是将光学图像转换为电子信号的半导体元件。他们在检测光时都采用光电二极管&#…...

【人工智能】第四部分:ChatGPT的技术实现
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...

小程序配置自定义tabBar及异形tabBar配置操作
什么是tabBar? 小程序的tabbar是指小程序底部的一组固定导航按钮,通常包含2-5个按钮,用于快速切换小程序的不同页面。每个按钮都有一个图标和文本标签,点击按钮可以切换到对应的页面。tabbar通常放置在小程序的底部,以…...

解析《动物园规则怪谈》【逻辑】
鉴赏《动物园规则怪谈》【逻辑】 前言版权推荐鉴赏《动物园规则怪谈》推理游客正方“它”方其他物品 不同规则或纸条的对比联系出现的地方及联系游客入园历程:被“它”污染的过程鉴赏升华 最后 前言 2024-5-31 13:05:38 以下内容源自《【逻辑】》 仅供学习交流使用…...
上传RKP 证书签名请求息上传到 Google 的后端服务器
上传证书签名请求 1.准备环境:OK pip3 install google-auth2.13.0 requests2.28下载 device_info_uploader.py 。 没找到先跳过 选项 1:通过 GCP 帐户使用 device_info_uploader.py 运行脚本。 ./device_info_uploader.py --credentials /secure/s…...

Debian和ubuntu 嵌入式的系统的 区别
随着开源操作系统的日益流行,Debian和Ubuntu这两个基于Linux的发行版本成为了众多开发者和系统管理员的首选。它们各自拥有独特的优势和特点,那么,在选择时,哪一个更适合你呢?接下来,我们将深入探讨两者的关…...

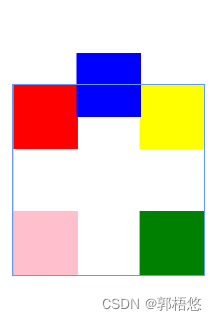
HTML旋转照片盒子
效果图 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><meta http-equiv"X-UA-Compatible" content…...
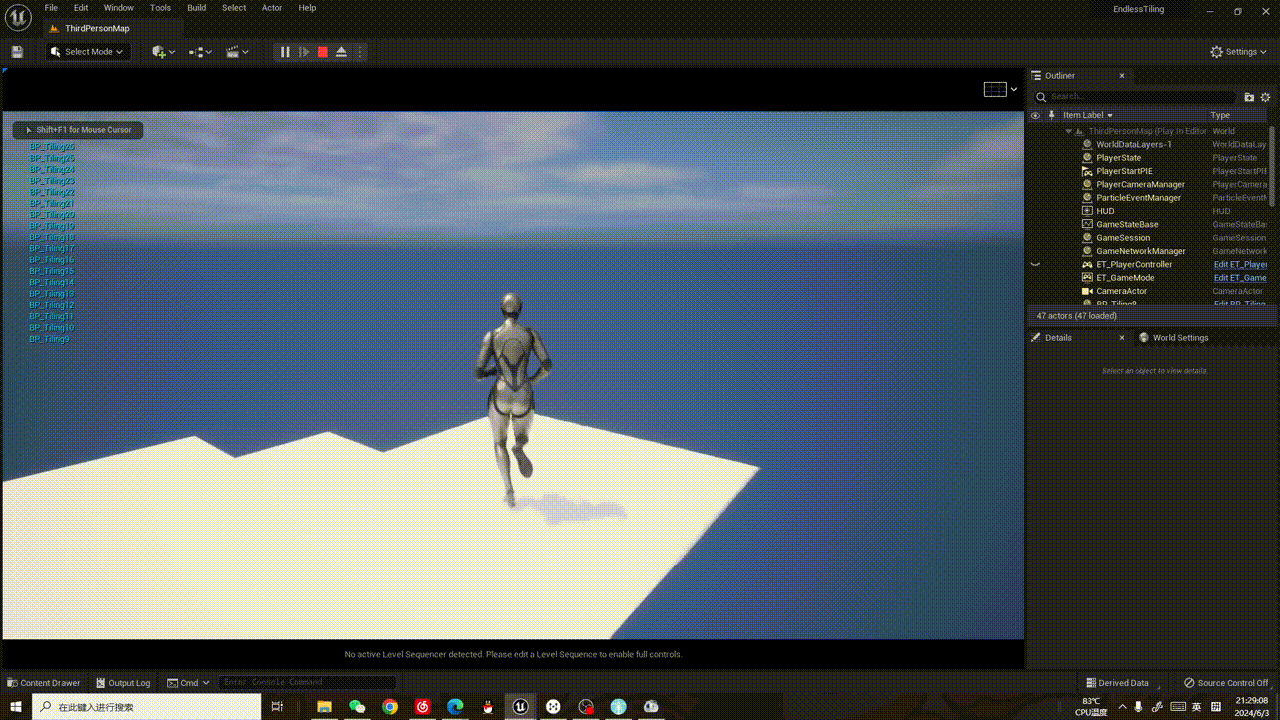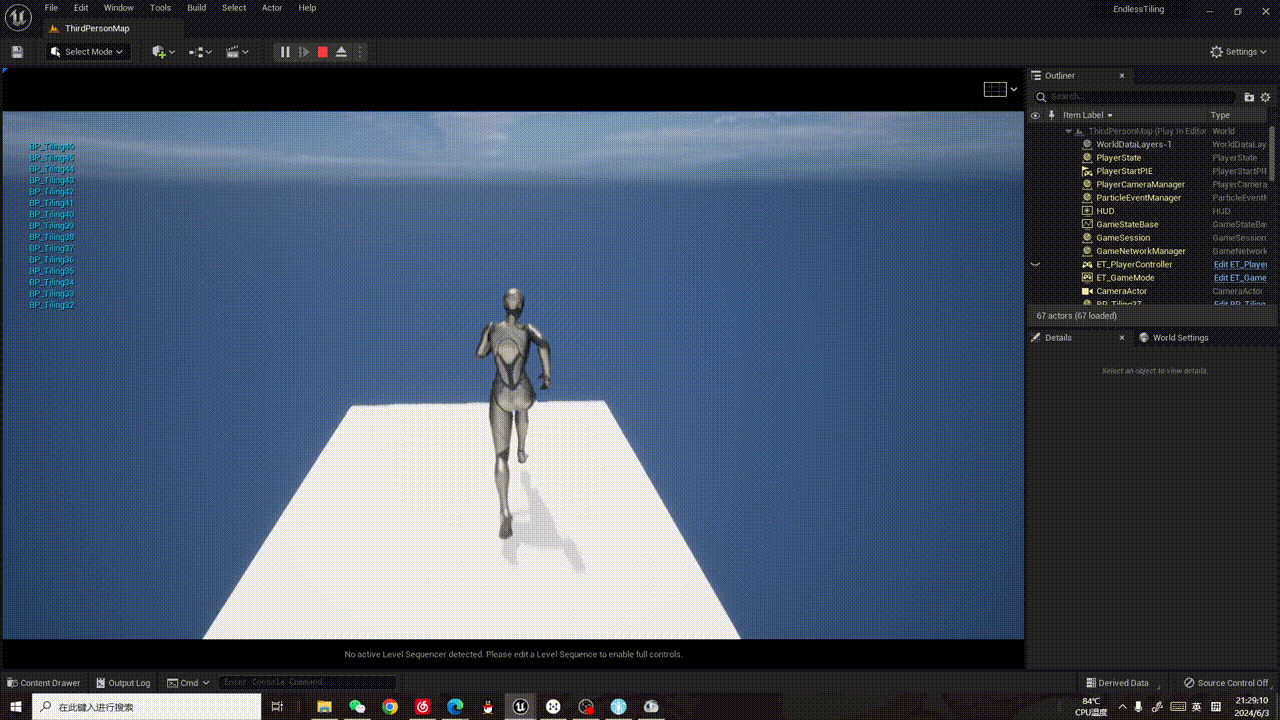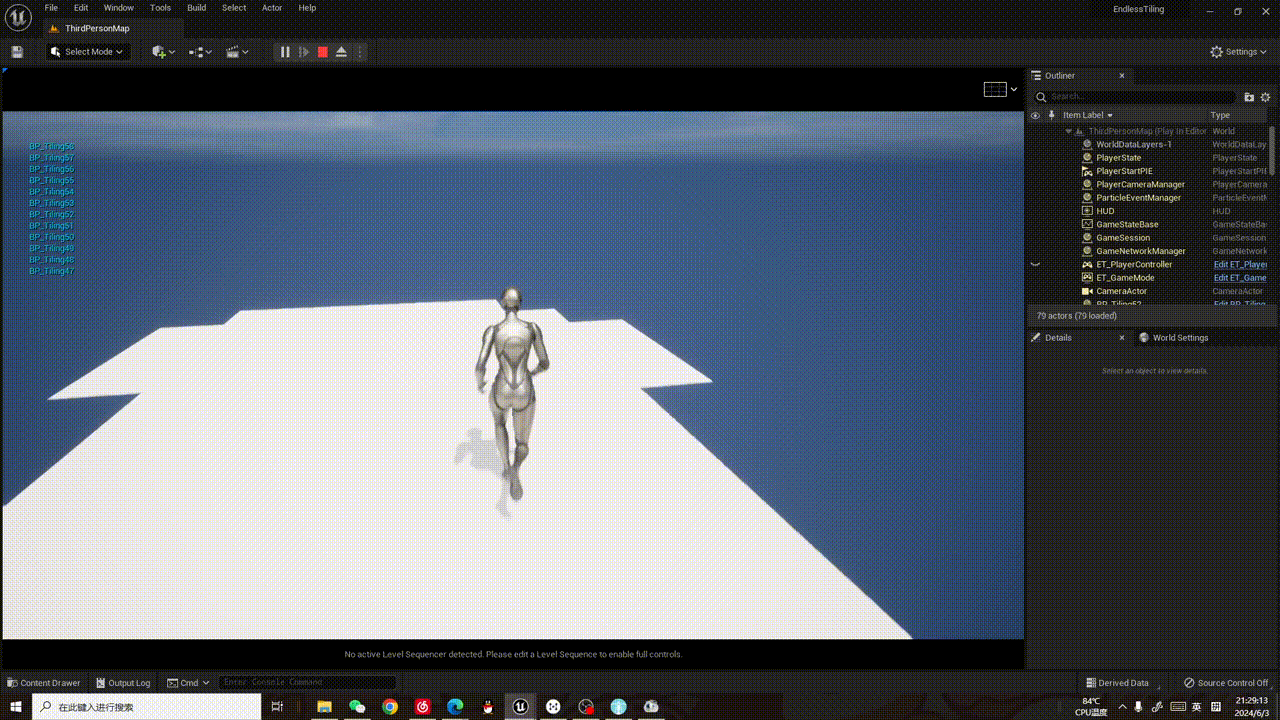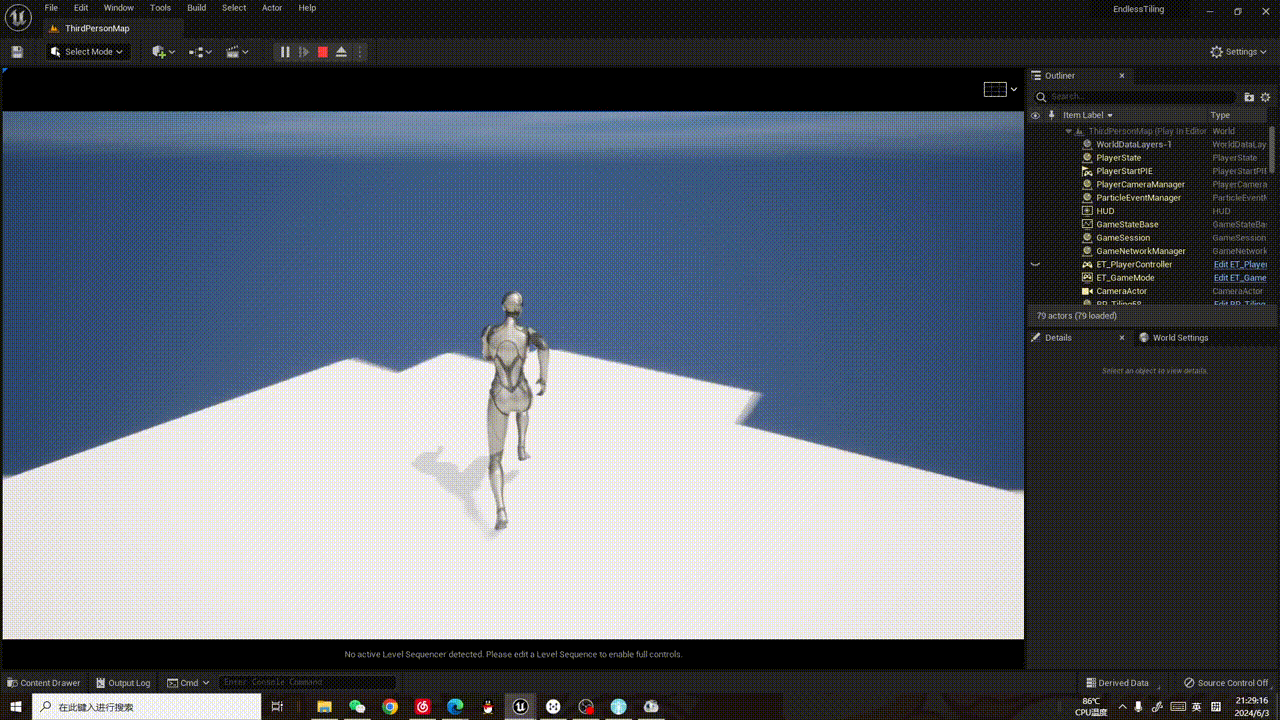
【UE5 刺客信条动态地面复刻】实现无界地面01:动态生成
2024.6.4更新 昨天半夜意识到生成Cube的方案不合适,又开始到处找动态地面的方法,发现了我想要的效果直接可以用nigara实现!!!! 于是这个部分就暂时告一段落,今季开始新的方向的学习。 为了快速…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
