Python | C# | MATLAB 库卡机器人微分运动学 | 欧拉-拉格朗日动力学 | 混合动力控制
🎯要点
🎯正向运动学几何矩阵,Python虚拟机器人模拟动画二连杆平面机械臂 | 🎯 逆向运动学几何矩阵,Python虚拟机器人模拟动画三连杆平面机械臂 | 🎯微分运动学数学形态,Python模拟近似结果 | 🎯欧拉-拉格朗日动力学数学形态,Python模拟机器人操纵器推导的运动方程有效性 | 🎯运动规划算法,Python虚拟机器人和摄像头模拟离线运动规划算法 | 🎯移动导航卡尔曼滤波算法及其它方法,Python虚拟机器人模拟可检测和可磕碰 | 🎯混合动力控制微分数学形态,Python虚拟机器人模拟比例微分积分和逆动态控制 | 🎯阻抗控制,Python模拟二联(三联动)。
🎯 库卡机器人模拟 ,库卡实体机器人对象检测和颜色分割拾取和放置物体 | 🎯 C#远程测试虚拟机器人 | 🎯虚拟机器人从三维文件创建自定义模型。
🎯Cpp(Python)和MATLAB差动驱动ROS Raspberry Pi全功能机器人原型。
🍇Python逆动力学算法
逆动力学是指计算运动中的力。给定配置 q q q、广义速度 q ˙ \dot{ q } q˙ 和广义加速度 q ¨ \ddot{ q } q¨,相当于找到关节扭矩 τ \tau τ 和接触力 f ext f ^{\text {ext } } fext 使得运动约束方程得到满足:
M ( q ) q ¨ + q ˙ ⊤ C ( q ) q ˙ = S ⊤ τ + τ g ( q ) + τ est + J ( q ) ⊤ f ext J ( q ) q ¨ + q ˙ ⊤ H ( q ) q ˙ = 0 \begin{aligned} M ( q ) \ddot{ q }+\dot{ q }^{\top} C ( q ) \dot{ q } & = S ^{\top} \tau + \tau _g( q )+ \tau ^{\text {est }}+ J ( q )^{\top} f ^{\text {ext }} \\ J ( q ) \ddot{ q }+\dot{ q }^{\top} H ( q ) \dot{ q } & = 0 \end{aligned} M(q)q¨+q˙⊤C(q)q˙J(q)q¨+q˙⊤H(q)q˙=S⊤τ+τg(q)+τest +J(q)⊤fext =0
逆动力学的数学函数如下:
( τ , f e x t ) = ID ( q , q ˙ , q ¨ ) \left(\tau, f ^{e x t}\right)=\operatorname{ID}( q , \dot{ q }, \ddot{ q }) (τ,fext)=ID(q,q˙,q¨)
当我们的线性系统完全确定时,该函数定义明确,例如对于具有六个自由度的手臂,但对于在多个接触下的移动机器人,该函数通常是欠确定的。在这种情况下,我们可以将外力的计算转移到例如接触模型,并仅计算关节扭矩:
τ = RNEA ( q , q ˙ , q ¨ , f est ) \tau =\operatorname{RNEA}\left( q , \dot{ q }, \ddot{ q }, f ^{\text {est }}\right) τ=RNEA(q,q˙,q¨,fest )
递归牛顿-欧拉算法为我们提供了一种实现此功能的有效方法。该算法分为两步:前向传递,主要是二阶正向运动学,然后是后向传递,计算力和关节扭矩。
此算法第一遍计算主体速度 v i v _i vi 和加速度 a i a _i ai。从运动树的根 i = 0 i=0 i=0 开始,物体 i i i 的运动 v i , a i v _i, a _i vi,ai 是根据运动 v λ ( i ) , a λ ( i ) v _{\lambda(i)}, a _{\lambda( i)} vλ(i),aλ(i) 其父体 λ ( i ) \lambda(i) λ(i) 的分量,加上它们之间的关节的运动 q ˙ i , q ¨ i \dot{ q }_i, \ddot{ q }_i q˙i,q¨i 引起的分量。让我们从主体速度开始:
v i = i X λ ( i ) v λ ( i ) + S i q ˙ i v _i={ }^i X _{\lambda(i)} v _{\lambda(i)}+ S _i \dot{ q }_i vi=iXλ(i)vλ(i)+Siq˙i
在此方程中, i X λ ( i ) { }^i X _{\lambda(i)} iXλ(i) 是从 λ ( i ) \lambda(i) λ(i) 到 i i i 的 Plücker 变换, S i S _i Si 是关节的运动子空间矩阵。请注意, q ˙ i ∈ R k \dot{ q }_i \in R ^k q˙i∈Rk 是关节的速度,例如对于浮动底座(又名自由飞行器)关节, k = 6 k=6 k=6,对于球形关节, k = 2 k=2 k=2,对于旋转关节或棱柱关节, k = 1 k=1 k=1。无论如何, q ˙ i \dot{ q }_i q˙i 不是广义速度向量 q ˙ \dot{ q } q˙ 的 i th i^{\text {th }} ith 分量(这没有意义,因为 i i i 是关节的索引,而向量 q ˙ \dot{ q } q˙ 按自由度索引)。因此,运动子空间矩阵的维度为 6 × k 6 \times k 6×k。
接下来,让我们假设一个“常见”关节(旋转关节、棱柱关节、螺旋关节、圆柱关节、平面关节、球形关节、自由飞行关节),这样运动子空间矩阵的视在时间导数为零。除非你处理的是不同的关节,否则不要介意这句话。 然后,在前向传递过程中从父关节计算出的主体加速度为:
a i = i X λ ( i ) a λ ( i ) + S i q ¨ i + v i × S i q ˙ i a _i={ }^i X _{\lambda(i)} a _{\lambda(i)}+ S _i \ddot{ q }_i+ v _i \times S _i \dot{ q }_i ai=iXλ(i)aλ(i)+Siq¨i+vi×Siq˙i
到目前为止,该正向传递是二阶正向运动学。一路上我们要计算的最后一件事是由主体运动 v i v _i vi , a i a _i ai产生的主体惯性力:
f i = I i a i + v i × ∗ I i v i − f i est f _i= I _i a _i+ v _i \times{ }^* I _i v _i- f _i^{\text {est }} fi=Iiai+vi×∗Iivi−fiest
我们将在向后传递期间更新这些力向量。请注意,由于它们是力矢量,因此我们的符号意味着 f i ext f _i^{\text {ext }} fiext 也是一个物体力矢量。如果外力在惯性系中表示为 0 f i ext { }^0 f _i^{\text {ext }} 0fiext ,则可以通过以 f i = i X 0 0 f i e x t f _i={ }^i X _0{ }^0 f _i^{e x t} fi=iX00fiext 映射到主体框架 。
此算法的第二遍计算体积力。从运动树的叶节点开始,物体 i i i 的广义力 f i f _i fi 被添加到迄今为止为其父代 λ ( i ) \lambda(i) λ(i) 计算的力 f λ ( i ) f _{\lambda(i)} fλ(i) :
f λ ( i ) = f λ ( i ) + i X λ ( i ) ⊤ f i f _{\lambda(i)}= f _{\lambda(i)}+{ }^i X _{\lambda(i)}^{\top} f _i fλ(i)=fλ(i)+iXλ(i)⊤fi
一旦计算出主体 i i i 上的广义力 f i f _i fi,我们就可以通过沿关节轴投影该 6D 主体矢量来获得相应的关节扭矩 τ i \tau _i τi:
τ i = S i ⊤ f i \tau _i= S _i^{\top} f _i τi=Si⊤fi
对于旋转关节, S i S _i Si 是一个 6 × 1 6 \times 1 6×1 列向量,因此我们以单个数字 τ i = S i ⊤ f i \tau_i= S _i^{\top} f _i τi=Si⊤fi 结尾:关节伺服系统应提供的驱动扭矩提供跟踪 ( q , q ˙ , q ¨ , f e x t ) \left( q , \dot{ q }, \ddot{ q }, f ^{e x t}\right) (q,q˙,q¨,fext)。所有其他组件对应于我们的旋转关节的五度约束,并将由关节的力学被动提供。
现在让我们通过在伪 Python 中执行相同的操作来明确更多的事情。我们的(此算法)函数原型是:
def rnea(q, qd, qdd, f_ext):pass
请注意,q 是每个关节的广义坐标列表,而不是平面数组,其他参数也是如此。特别是,f_ext 是体力矢量 f i ext f _i^{\text {ext }} fiext 的列表。使用 Python 类型注释,我们的原型将如下所示:
from typing import Listimport numpy as npdef rnea(q: List[np.ndarray],qd: List[np.ndarray],qdd: List[np.ndarray],f_ext: List[np.ndarray],
) -> List[np.ndarray]:pass
这种额外的结构允许更通用的关节,例如球形关节(不常见)或用于移动机器人浮动底座的自由飞行关节(常见)。如果所有关节都是旋转的,那么所有类型都将合并为平面阵列。
让我们用 v 0 = 0 v _0= 0 v0=0 表示运动树根链接的空间速度,用 a 0 a _0 a0 表示其空间加速度。我们将它们分别初始化为零和标准重力加速度:
n = len(qd) - 1 # number of links == number of joints - 1
v = [np.empty((6,)) for i in range(n + 1)]
a = [np.empty((6,)) for i in range(n + 1)]
f = [np.empty((6,)) for i in range(n + 1)]
tau = [np.empty(qd[i].shape) for i in range(n + 1)]
v[0] = np.zeros((6,))
a[0] = -np.array([0.0, 0.0, -9.81])
我们继续前向传递,范围从链接 i = 1 i=1 i=1 到树的最后一个链接 i = n i=n i=n:
for i in range(1, n + 1):p = lambda_[i] # p for "parent"X_p_to_i[i], S[i], I[i] = compute_joint(joint_type[i], q[i])v[i] = X_p_to_i[i] * v[p] + S[i] * qd[i]a[i] = X_p_to_i[i] * a[p] + S[i] * qdd[i] + spatial_cross(v[i], S[i] * qd[i])f[i] = I[i] * a[i] + spatial_cross_dual(v[i], I[i] * v[i]) - f_ext[i]
向后传递以相反的顺序遍历相同的范围:
for i in range(n, 0, -1):p = lambda_[i]tau[i] = S[i].T * f[i]f[p] += X_p_to_i[i].T * f[i]
最终,我们得到:
def rnea(q, qd, qdd, f_ext):n = len(qd)v = [np.empty((6,)) for i in range(n + 1)]a = [np.empty((6,)) for i in range(n + 1)]f = [np.empty((6,)) for i in range(n + 1)]tau = [np.empty(qd[i].shape) for i in range(n + 1)]v[0] = np.zeros((6,))a[0] = -np.array([0.0, 0.0, -9.81])for i in range(1, n + 1):p = lambda_[i]X_p_to_i[i], S[i], I[i] = compute_joint(joint_type[i], q[i])v[i] = X_p_to_i[i] * v[p] + S[i] * qd[i]a[i] = X_p_to_i[i] * a[p] + S[i] * qdd[i] + spatial_cross(v[i], S[i] * qd[i])f[i] = I[i] * a[i] + spatial_cross_dual(v[i], I[i] * v[i]) - f_ext[i]for i in range(n, 0, -1):p = lambda_[i]tau[i] = S[i].T * f[i]f[p] += X_p_to_i[i].T * f[i]return tau
长度不同的数组列表通常是刚体动力学库或模拟器中的内部结构。从此类列表到平面数组结构的映射称为关节,并决定如何表示球形和自由飞行关节的方向。
👉参阅:亚图跨际
相关文章:

Python | C# | MATLAB 库卡机器人微分运动学 | 欧拉-拉格朗日动力学 | 混合动力控制
🎯要点 🎯正向运动学几何矩阵,Python虚拟机器人模拟动画二连杆平面机械臂 | 🎯 逆向运动学几何矩阵,Python虚拟机器人模拟动画三连杆平面机械臂 | 🎯微分运动学数学形态,Python模拟近似结果 | …...
Signac|成年小鼠大脑 单细胞ATAC分析(1)
引言 在本教程中,我们将探讨由10x Genomics公司提供的成年小鼠大脑细胞的单细胞ATAC-seq数据集。本教程中使用的所有相关文件均可在10x Genomics官方网站上获取。 本教程复现了之前在人类外周血单核细胞(PBMC)的Signac入门教程中执行的命令。…...

【POSIX】运行时so库动态加载
运行时可以自己自定义so库的动态加载框架,主动去加载某些库,并调用其中的某些方法 首先写一些方法,并生成so库 // hello.cpp#include <iostream>/*使用 nm 命令查看 so 库的内容 */// 1. 使用extern // dlsym(handle, "hello&qu…...
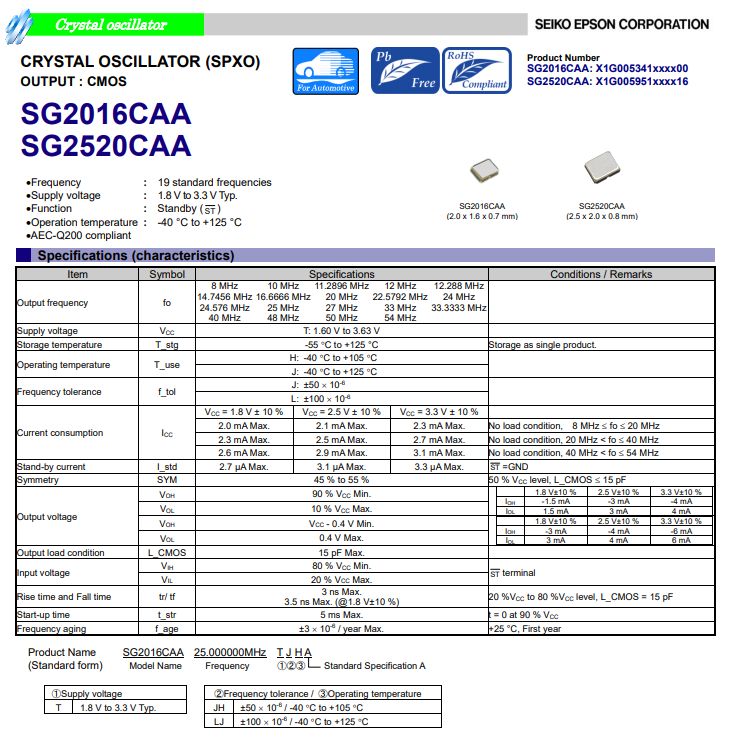
爱普生SG2520CAA汽车电子中控专用晶振
随着汽车电子技术的飞速发展,汽车中控系统变得越来越智能化和复杂化。为了确保这些系统的高性能和高可靠性,选择符合AEC-Q200标准的高品质晶振至关重要。爱普生SG2520CAA晶振凭借其优异的特性,成为汽车电子中控系统的理想选择。 爱普生晶振SG…...
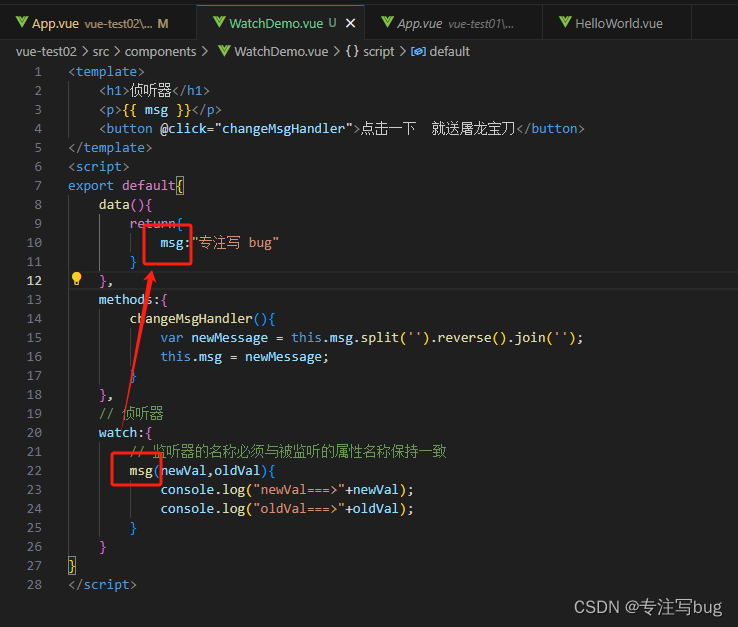
Vue——监听器简单使用与注意事项
文章目录 前言编写简单demo注意事项 前言 监听器,在官网中称为侦听器,个人还是喜欢称之为监听器。官方文档如下: vue 官网 侦听器 编写简单demo 侦听器在项目中通常用于监听某个属性变量值的变化,并根据该变化做出一些处理操作。…...

OpenCV的“画笔”功能
类似于画图软件的自由笔刷功能,当按住鼠标左键,在屏幕上画出连续的线条。 定义函数: import cv2 import numpy as np# 初始化参数 drawing False # 鼠标左键按下时为True ix, iy -1, -1 # 鼠标初始位置# 鼠标回调函数 def mouse_paint(…...
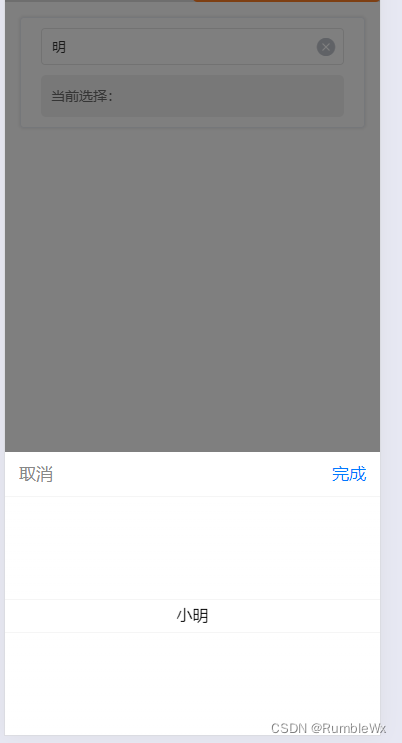
uniapp封装picker选择器组件,支持关键字查询
CommonPicker.vue组件 路径在 components\CommonPicker.vue <template><view><uni-easyinput v-model"searchQuery" :placeholder"placeholder" /><picker :range"filteredOptions" :range-key"text" v-model&…...
智慧城市的规划与实施:科技引领城市运行效率新飞跃
随着信息技术的飞速发展,智慧城市的构想正逐步成为现实。作为地理信息与遥感领域的研究者,我深知在这一转型过程中,技术的创新与应用是提升城市运行效率的关键。本文旨在探讨如何利用地理信息系统(GIS)、遥感技术、大数…...
Linux——内存管理代码分析
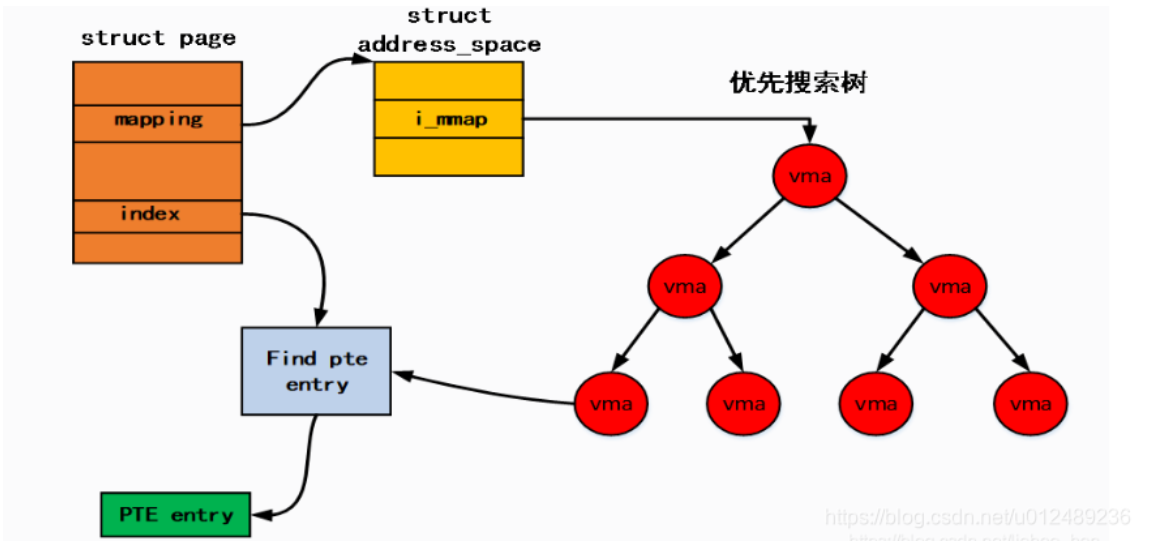
虚空间管理 页框和页的关系 页框 将内存空间分为一个个大小相等的分区(比如:每个分区4KB),每个分区就是一个页框,也叫页帧,即物理页面,是linux划分内存空间的结果。 每个页框都有一个页框号,即内存块号、物理块号。 页 将用户…...
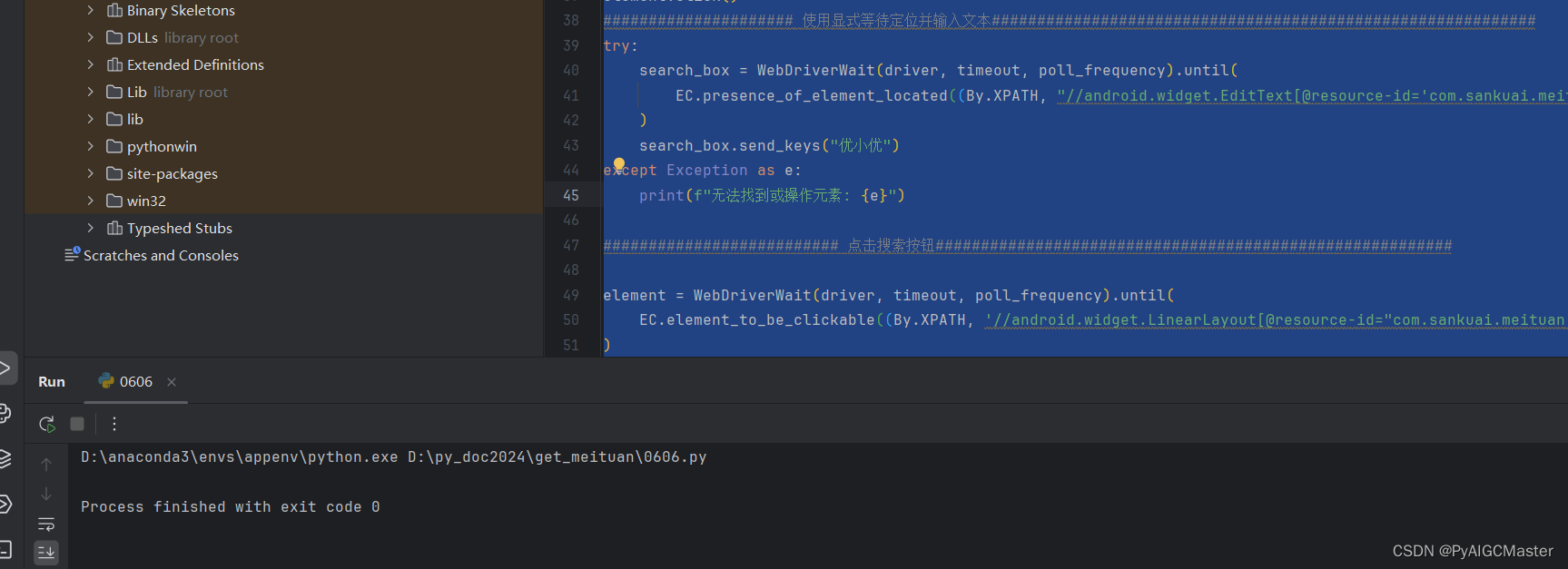
手机自动化测试:4.通过appium inspector 获取相关app的信息,以某团为例,点击,搜索,获取数据等。
0.使用inspector时,一定要把不相关的如weditor啥的退出去,否则,净是事。 1.从0开始的数据获取 第一个位置,有时0.0.0.0,不可以的话,你就用这个。 第二个位置,抄上。 直接点击第三个启动。不要…...
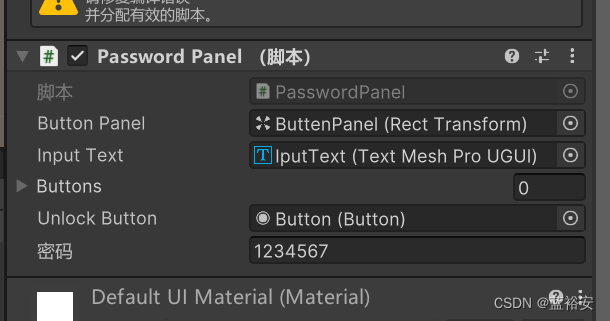
个人项目———密码锁的实现
布局组件 布局效果 组件绑定 密码锁的实现代码 using TMPro; using UnityEngine; using UnityEngine.UI;public class PasswordPanel : MonoBehaviour {// public Button button;// 所有按键的父物体public Transform buttonPanel;// 输入字符串的文本框public TMP_Text input…...

关于Input【type=number】可以输入e问题及解决方案
一、为什么 因为在数学里e 代表无理数,e是自然对数的底数,同时它又是一个无限不循环小数,所以我们在输入 e 时,输入框会默认 e 是数字,从而没有对它进行限制。 二、解决方案 小提示:vue下监听事件需要加n…...
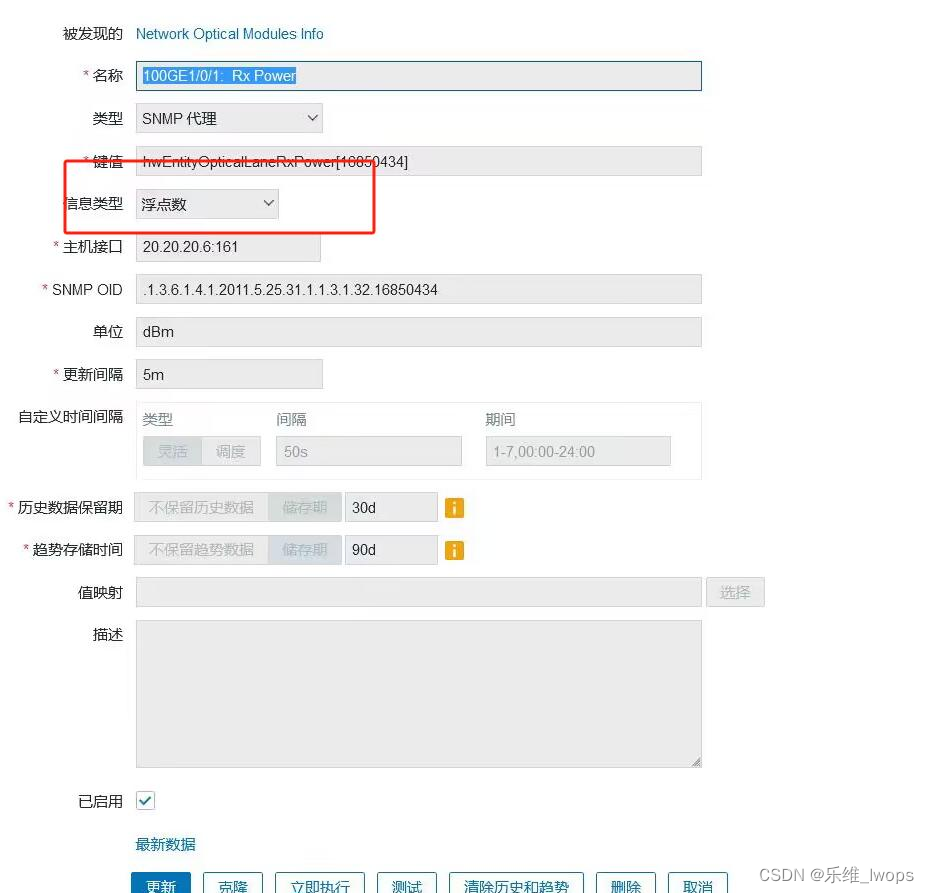
zabbix“专家坐诊”第241期问答
问题一 Q:华为交换机的100GE 1/0/1口的光模块收光值监测不到,有没有人碰到过这个问题呢?其他的端口都能监测到收光值,但是100GE 1/0/1口监测不到收光值。底层能查到,zabbix 6.0监控不到,以下是端口的报错信…...
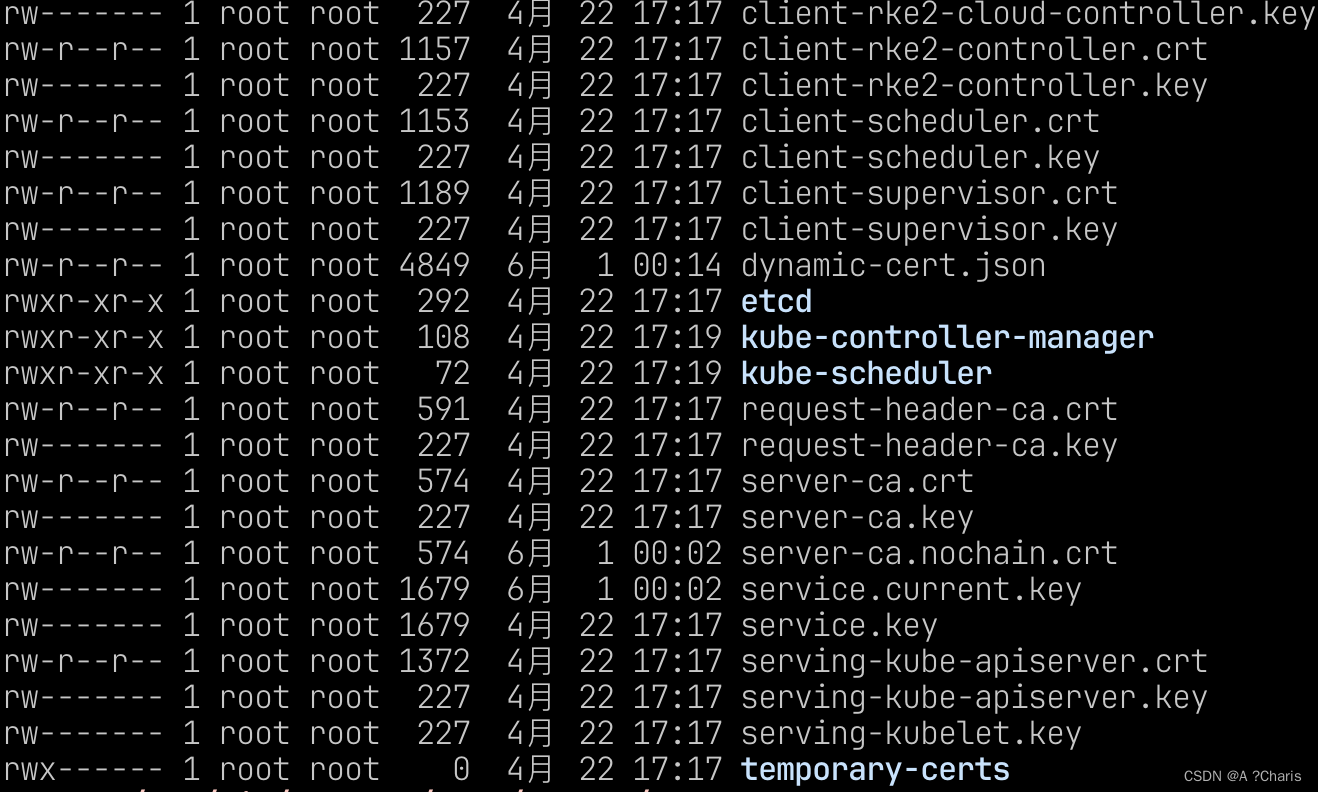
了解Kubernetes-RKE2的PKI以及证书存放位置
一、什么是PKI? 简称:证书基础设施。 可以方便理解为当你的集群有Server,Client架构,那么为了安全加密之间的通信,则需要使用证书进行交互,那么利用PKI架构可以安全加密组件之间的通信。 二、Kubernetes的PKI架构什…...

利用大语言模型进行事实匹配
论文地址:Automated Claim Matching with Large Language Models: Empowering Fact-Checkers in the Fight Against Misinformation | Companion Proceedings of the ACM on Web Conference 2024 WWW 2024 Automated Claim Matching with Large Language Models: Empowering F…...

【Stable Diffusion】(基础篇一)—— Stable Diffusion的安装
本系列笔记主要参考B站nenly同学的视频教程,传送门:B站第一套系统的AI绘画课!零基础学会Stable Diffusion,这绝对是你看过的最容易上手的AI绘画教程 | SD WebUI 保姆级攻略_哔哩哔哩_bilibili **Stable Diffusion(简称…...

维纳运动的概念
维纳运动(Wiener Process),也称为标准布朗运动,是一种重要的随机过程,广泛应用于数学、物理学和金融学等领域。它是一个连续时间的随机过程,具有一些特殊的性质,使其成为描述随机动态系统的经典…...
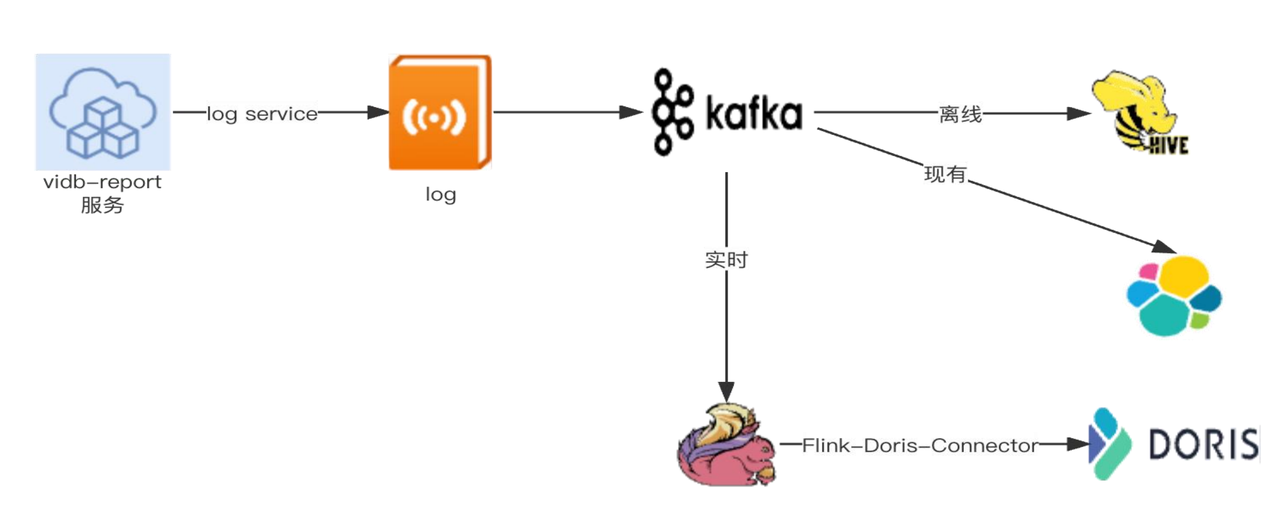
毫秒级查询性能优化实践!Apache Doris 在极越汽车数字化运营和营销方向的解决方案
作者:韩同阳,极越汽车大数据架构师,Apache Doris Active Contributor 编辑整理:SelectDB 技术团队 导读:极越是高端智能汽车机器人品牌,基于领先的百度 AI 能力和吉利 SEA 浩瀚架构生态赋能,致…...

vllm 大模型量化微调推理使用: lora、gptq、awq
1)微调lora模型推理 docker run --gpus all -v /ai/Qwen1.5-7B-Chat:/qwen-7b -v /ai/lora:/lora -p 10860:10860 --...
 自动测评方法)
WPS/Office(Word、Excel、PPT) 自动测评方法
在各高等、中等院校的计算机类课程中,计算机基本应用技能的上机操作考试,广受重视,大为盛行。其中,office(word、excel、ppt)上机考试最为普遍。于是,实现这类Office文档操作的自动阅卷评分,很有必要。本人最近项目上刚好遇到需要解决这种自动评分的问题,所以再次记录下解决的…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
