Codeforces Round 951 (Div. 2) C、D(构造、线段树)
1979C - Earning on Bets

构造题:观察到k范围很小,首先考虑最终硬币总数可以是多少,我们可以先假设最终的硬币总数为所有k取值的最小公倍数,这样只需要满足每个结果添加1枚硬币即可赚到硬币。
// Problem: C. Earning on Bets
// Contest: Codeforces - Codeforces Round 951 (Div. 2)
// URL: https://codeforces.com/contest/1979/problem/C
// Memory Limit: 256 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
#define int long long
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{int n;cin >> n;LL ans = 1;for(int i = 2 ; i <= 20 ; i ++){ans = lcm(ans , i);}int tot = 0;for(int i = 0 ; i < n ; i ++){cin >> a[i];tot += ans / a[i];}int res = ans - tot;if(res < n){cout << -1 << endl;}else{for(int i = 0 ; i < n - 1; i ++){cout << ans / a[i] + 1 << " ";res--;}cout << ans / a[n - 1] + res << endl;}
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
1979D - Fixing a Binary String
题意:
翻译有误,请看英文题面
思路:典型的一个区间合并求数量问题,我们可以直接构造两颗线段树解决。
// Problem: D. Fixing a Binary String
// Contest: Codeforces - Codeforces Round 951 (Div. 2)
// URL: https://codeforces.com/contest/1979/problem/D
// Memory Limit: 256 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}template<class Info>
struct SegmentTree {int n;std::vector<Info> info;SegmentTree() : n(0) {}SegmentTree(int n_, Info v_ = Info()) {init(n_, v_);}template<class T>SegmentTree(std::vector<T> init_) {init(init_);}template<class T>void init(std::vector<T> init_) {n = init_.size();info.assign(4 << std::__lg(n), Info());std::function<void(int, int, int)> build = [&](int p, int l, int r) {if (r - l == 1) {info[p] = init_[l];return;}int m = (l + r) / 2;build(2 * p, l, m);build(2 * p + 1, m, r);pull(p);};build(1, 0, n);}void pull(int p) {info[p] = info[2 * p] + info[2 * p + 1];}void modify(int p, int l, int r, int x, const Info &v) {if (r - l == 1) {info[p] = info[p] + v;return;}int m = (l + r) / 2;if (x < m) {modify(2 * p, l, m, x, v);} else {modify(2 * p + 1, m, r, x, v);}pull(p);}void modify(int p, const Info &v) {modify(1, 0, n, p, v);}Info rangeQuery(int p, int l, int r, int x, int y) {if (l >= y || r <= x) {return Info();}if (l >= x && r <= y) {return info[p];}int m = (l + r) / 2;return rangeQuery(2 * p, l, m, x, y) + rangeQuery(2 * p + 1, m, r, x, y);}Info rangeQuery(int l, int r) {return rangeQuery(1, 0, n, l, r);}template<class F>int findFirst(int p, int l, int r, int x, int y, F pred) {if (l >= y || r <= x || !pred(info[p])) {return -1;}if (r - l == 1) {return l;}int m = (l + r) / 2;int res = findFirst(2 * p, l, m, x, y, pred);if (res == -1) {res = findFirst(2 * p + 1, m, r, x, y, pred);}return res;}template<class F>int findFirst(int l, int r, F pred) {return findFirst(1, 0, n, l, r, pred);}template<class F>int findLast(int p, int l, int r, int x, int y, F pred) {if (l >= y || r <= x || !pred(info[p])) {return -1;}if (r - l == 1) {return l;}int m = (l + r) / 2;int res = findLast(2 * p + 1, m, r, x, y, pred);if (res == -1) {res = findLast(2 * p, l, m, x, y, pred);}return res;}template<class F>int findLast(int l, int r, F pred) {return findLast(1, 0, n, l, r, pred);}
};struct Info {int left0 = 0, left1 = 0;int right0 = 0, right1 = 0;int cnt = 0;int act = 0;
};Info operator + (Info a, Info b) {if(a.act == 0){return b;}if(b.act == 0){return a;}Info c;c.left0 = a.left0;c.left1 = a.left1;c.right0 = b.right0;c.right1 = b.right1;c.act = a.act + b.act;c.cnt = a.cnt + b.cnt;if(a.right0 > 0 && b.left0 > 0){int tmp = a.right0 + b.left0;if(tmp > m){c.cnt = -1;}if(tmp == m){c.cnt++;}if(a.right0 == a.act){c.left0 = a.act + b.left0;}if(b.left0 == b.act){c.right0 = a.right0 + b.act;}if(a.right0 != a.act && b.left0 != b.act && tmp != m){c.cnt = -1;}}else if(a.right1 > 0 && b.left1 > 0){int tmp = a.right1 + b.left1;if(tmp > m){c.cnt = -1;}if(tmp == m){c.cnt++;}if(a.right1 == a.act){c.left1 = a.act + b.left1;}if(b.left1 == b.act){c.right1 = b.act + a.right1; }if(a.right1 != a.act && b.left1 != b.act && tmp != m){c.cnt = -1;}}else if(a.right0 > 0 && b.left1 > 0){int tmp1 = a.right0;int tmp2 = b.left1;if(b.left1 == b.act){c.right1 = b.act;}else if(b.left1 != m){c.cnt = -1;}if(a.right0 == a.act){c.left0 = a.act;}else if(a.right0 != m){c.cnt = -1;}}else if(a.right1 > 0 && b.left0 > 0){int tmp1 = a.right1;int tmp2 = b.left0;if(b.left0 == b.act){c.right0 = b.act;}else if(b.left0 != m){c.cnt = -1;}if(a.right1 == a.act){c.left1 = a.act;}else if(a.right1 != m){c.cnt = -1;} }return c;
}void solve()
{cin >> n >> m;string s;cin >> s;vector<Info>v;for(int i = 0 ; i < n ; i ++){Info tmp;if(s[i] == '1'){tmp.cnt = 0;tmp.act = 1;tmp.left1 = 1;tmp.right1 = 1;tmp.left0 = 0;tmp.right0 = 0;if(m == 1){tmp.cnt = 1;}}else{tmp.cnt = 0;tmp.act = 1;tmp.left1 = 0;tmp.right1 = 0;tmp.left0 = 1;tmp.right0 = 1; if(m == 1){tmp.cnt = 1;} }v.pb(tmp);}vector<Info>vv;for(int i = n - 1 ; i >= 0 ; i --){Info tmp;if(s[i] == '1'){tmp.cnt = 0;tmp.act = 1;tmp.left1 = 1;tmp.right1 = 1;tmp.left0 = 0;tmp.right0 = 0;if(m == 1){tmp.cnt = 1;} }else{tmp.cnt = 0;tmp.act = 1;tmp.left1 = 0;tmp.right1 = 0;tmp.left0 = 1;tmp.right0 = 1; if(m == 1){tmp.cnt = 1;} }vv.pb(tmp); }SegmentTree <Info> seg(v);SegmentTree<Info>seg2(vv);for(int i = 1 ; i <= n ; i ++){Info tmp1 = seg.rangeQuery(i , n);Info tmp2 = seg2.rangeQuery(n - i , n);Info tmp3 = tmp1 + tmp2;if(tmp3.cnt == n / m){cout << i << endl;return;}}cout << -1 << endl;
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
相关文章:

Codeforces Round 951 (Div. 2) C、D(构造、线段树)
1979C - Earning on Bets 构造题:观察到k范围很小,首先考虑最终硬币总数可以是多少,我们可以先假设最终的硬币总数为所有k取值的最小公倍数,这样只需要满足每个结果添加1枚硬币即可赚到硬币。 // Problem: C. Earning on Bets //…...

elmentUI el-table 总结行
背景 原因:表格展示的都是明细数据,需要对当前的明细数据的部分字段进行汇总难点:汇总的条件不一定,有时候客户查的是1天,有时候是10天 官方写法 只开启开关 开启汇总开关如果没有汇总方法, 会自动汇总所有…...
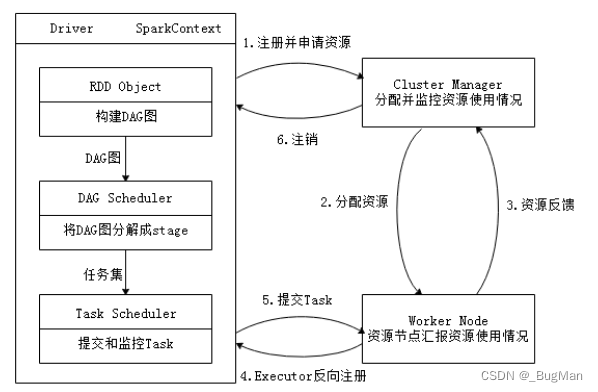
【大数据】计算引擎:Spark核心概念
目录 前言 1.什么是Spark 2.核心概念 2.1.Spark如何拉高计算性能 2.2.RDD 2.3.Stage 3.运行流程 前言 本文是作者大数据系列中的一文,专栏地址: https://blog.csdn.net/joker_zjn/category_12631789.html?spm1001.2014.3001.5482 该系列会成体…...

Python | C# | MATLAB 库卡机器人微分运动学 | 欧拉-拉格朗日动力学 | 混合动力控制
🎯要点 🎯正向运动学几何矩阵,Python虚拟机器人模拟动画二连杆平面机械臂 | 🎯 逆向运动学几何矩阵,Python虚拟机器人模拟动画三连杆平面机械臂 | 🎯微分运动学数学形态,Python模拟近似结果 | …...
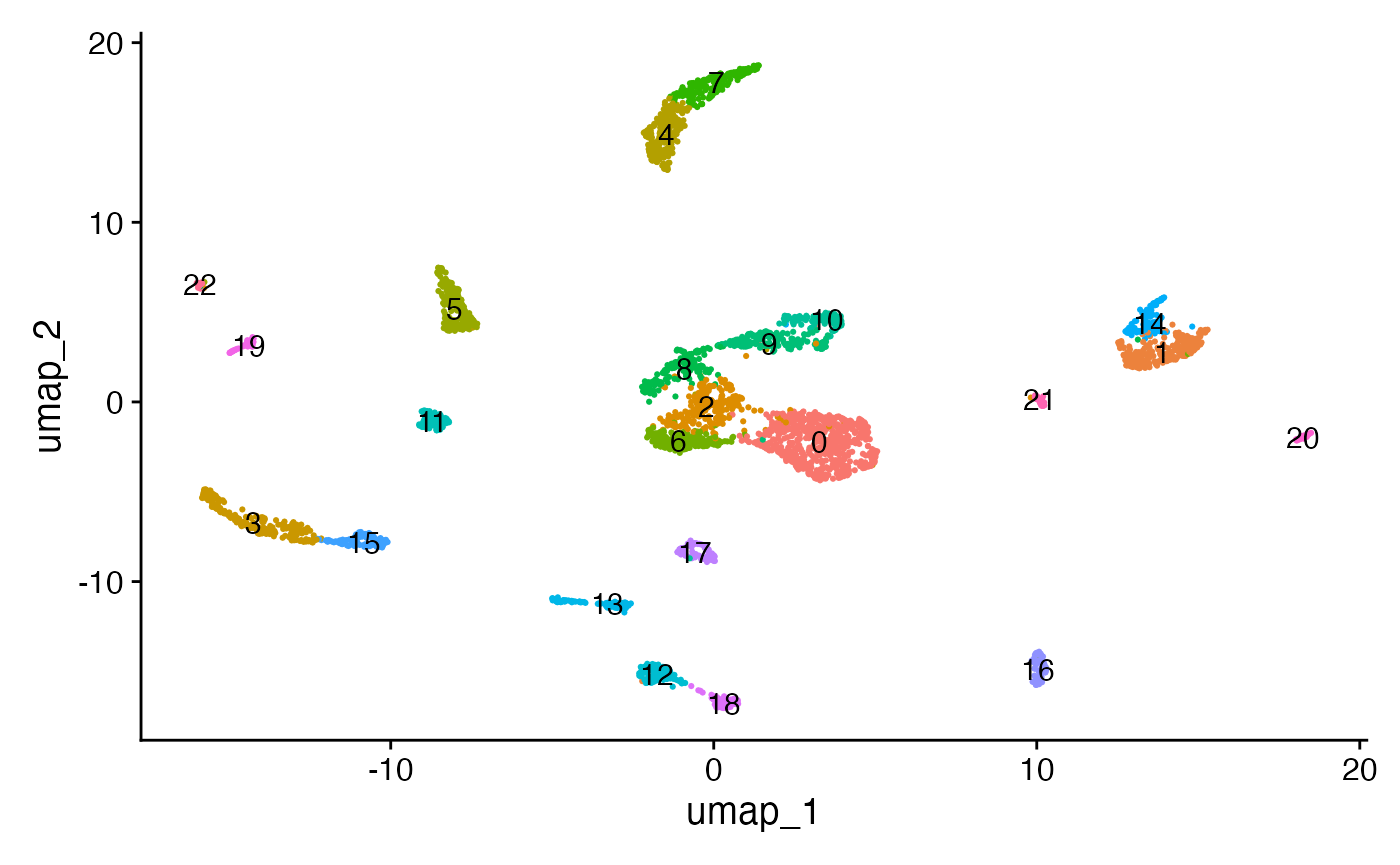
Signac|成年小鼠大脑 单细胞ATAC分析(1)
引言 在本教程中,我们将探讨由10x Genomics公司提供的成年小鼠大脑细胞的单细胞ATAC-seq数据集。本教程中使用的所有相关文件均可在10x Genomics官方网站上获取。 本教程复现了之前在人类外周血单核细胞(PBMC)的Signac入门教程中执行的命令。…...

【POSIX】运行时so库动态加载
运行时可以自己自定义so库的动态加载框架,主动去加载某些库,并调用其中的某些方法 首先写一些方法,并生成so库 // hello.cpp#include <iostream>/*使用 nm 命令查看 so 库的内容 */// 1. 使用extern // dlsym(handle, "hello&qu…...
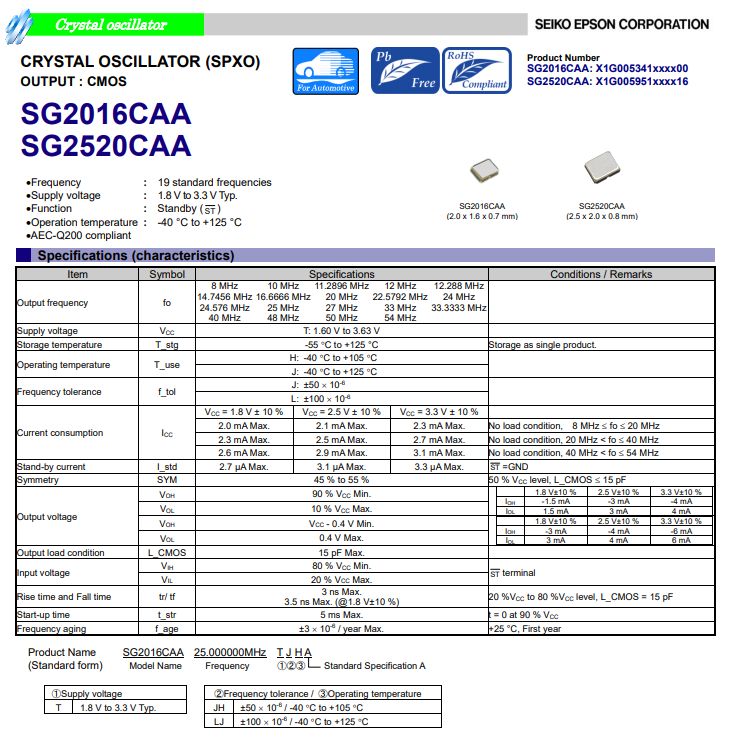
爱普生SG2520CAA汽车电子中控专用晶振
随着汽车电子技术的飞速发展,汽车中控系统变得越来越智能化和复杂化。为了确保这些系统的高性能和高可靠性,选择符合AEC-Q200标准的高品质晶振至关重要。爱普生SG2520CAA晶振凭借其优异的特性,成为汽车电子中控系统的理想选择。 爱普生晶振SG…...
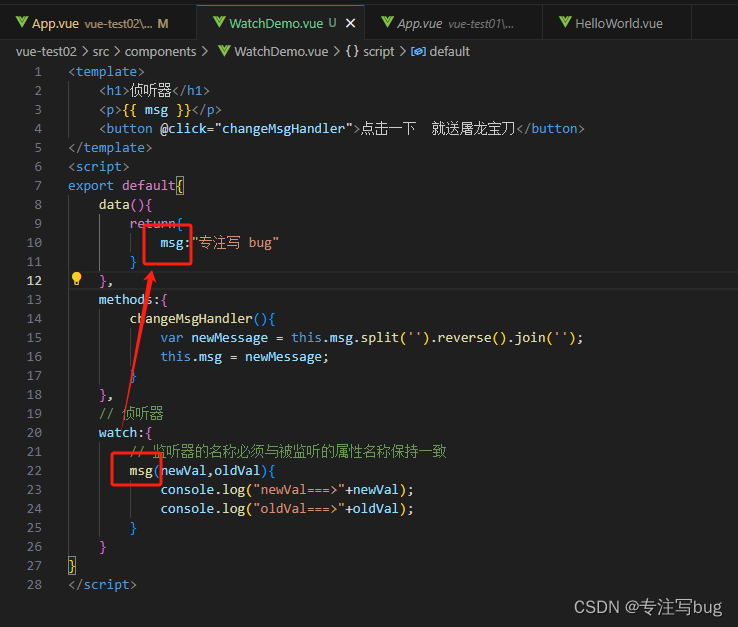
Vue——监听器简单使用与注意事项
文章目录 前言编写简单demo注意事项 前言 监听器,在官网中称为侦听器,个人还是喜欢称之为监听器。官方文档如下: vue 官网 侦听器 编写简单demo 侦听器在项目中通常用于监听某个属性变量值的变化,并根据该变化做出一些处理操作。…...

OpenCV的“画笔”功能
类似于画图软件的自由笔刷功能,当按住鼠标左键,在屏幕上画出连续的线条。 定义函数: import cv2 import numpy as np# 初始化参数 drawing False # 鼠标左键按下时为True ix, iy -1, -1 # 鼠标初始位置# 鼠标回调函数 def mouse_paint(…...
uniapp封装picker选择器组件,支持关键字查询
CommonPicker.vue组件 路径在 components\CommonPicker.vue <template><view><uni-easyinput v-model"searchQuery" :placeholder"placeholder" /><picker :range"filteredOptions" :range-key"text" v-model&…...
智慧城市的规划与实施:科技引领城市运行效率新飞跃
随着信息技术的飞速发展,智慧城市的构想正逐步成为现实。作为地理信息与遥感领域的研究者,我深知在这一转型过程中,技术的创新与应用是提升城市运行效率的关键。本文旨在探讨如何利用地理信息系统(GIS)、遥感技术、大数…...
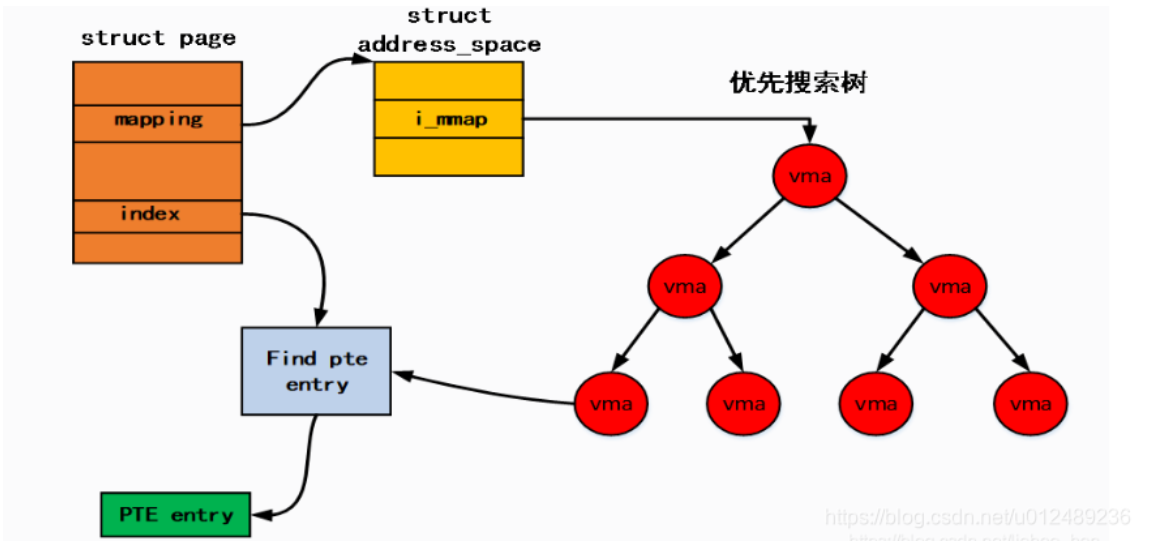
Linux——内存管理代码分析
虚空间管理 页框和页的关系 页框 将内存空间分为一个个大小相等的分区(比如:每个分区4KB),每个分区就是一个页框,也叫页帧,即物理页面,是linux划分内存空间的结果。 每个页框都有一个页框号,即内存块号、物理块号。 页 将用户…...
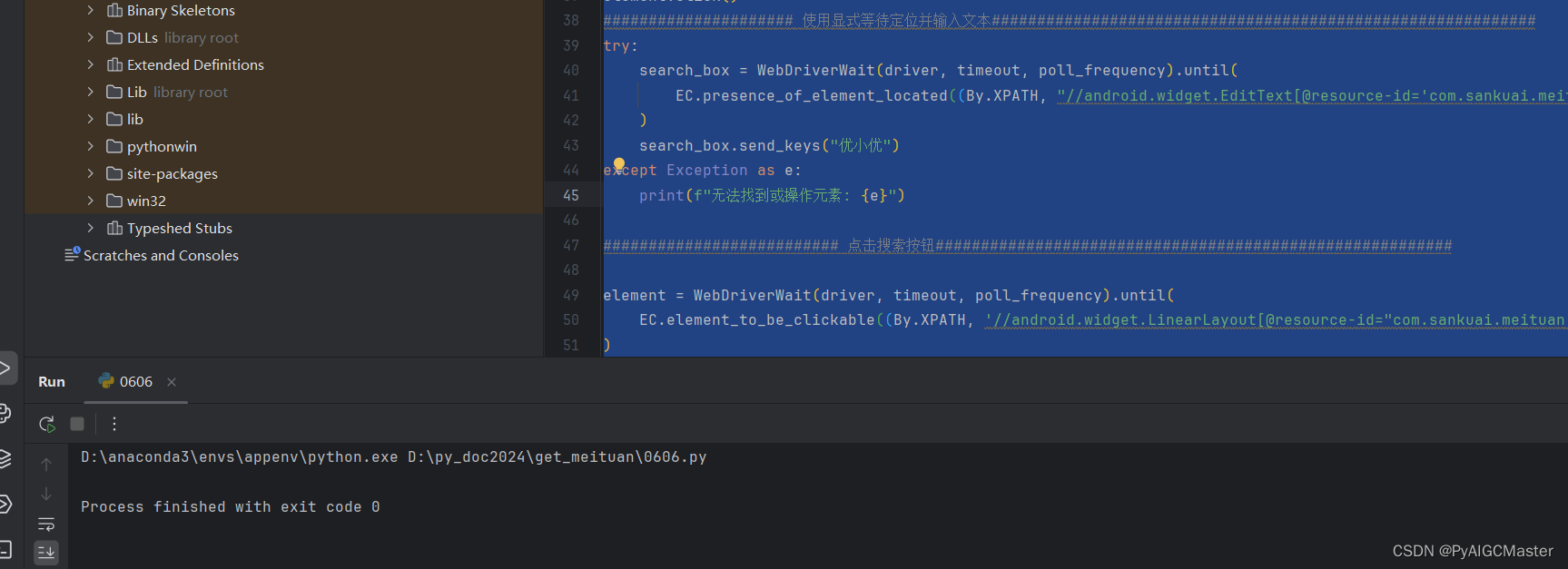
手机自动化测试:4.通过appium inspector 获取相关app的信息,以某团为例,点击,搜索,获取数据等。
0.使用inspector时,一定要把不相关的如weditor啥的退出去,否则,净是事。 1.从0开始的数据获取 第一个位置,有时0.0.0.0,不可以的话,你就用这个。 第二个位置,抄上。 直接点击第三个启动。不要…...
个人项目———密码锁的实现
布局组件 布局效果 组件绑定 密码锁的实现代码 using TMPro; using UnityEngine; using UnityEngine.UI;public class PasswordPanel : MonoBehaviour {// public Button button;// 所有按键的父物体public Transform buttonPanel;// 输入字符串的文本框public TMP_Text input…...

关于Input【type=number】可以输入e问题及解决方案
一、为什么 因为在数学里e 代表无理数,e是自然对数的底数,同时它又是一个无限不循环小数,所以我们在输入 e 时,输入框会默认 e 是数字,从而没有对它进行限制。 二、解决方案 小提示:vue下监听事件需要加n…...
zabbix“专家坐诊”第241期问答
问题一 Q:华为交换机的100GE 1/0/1口的光模块收光值监测不到,有没有人碰到过这个问题呢?其他的端口都能监测到收光值,但是100GE 1/0/1口监测不到收光值。底层能查到,zabbix 6.0监控不到,以下是端口的报错信…...
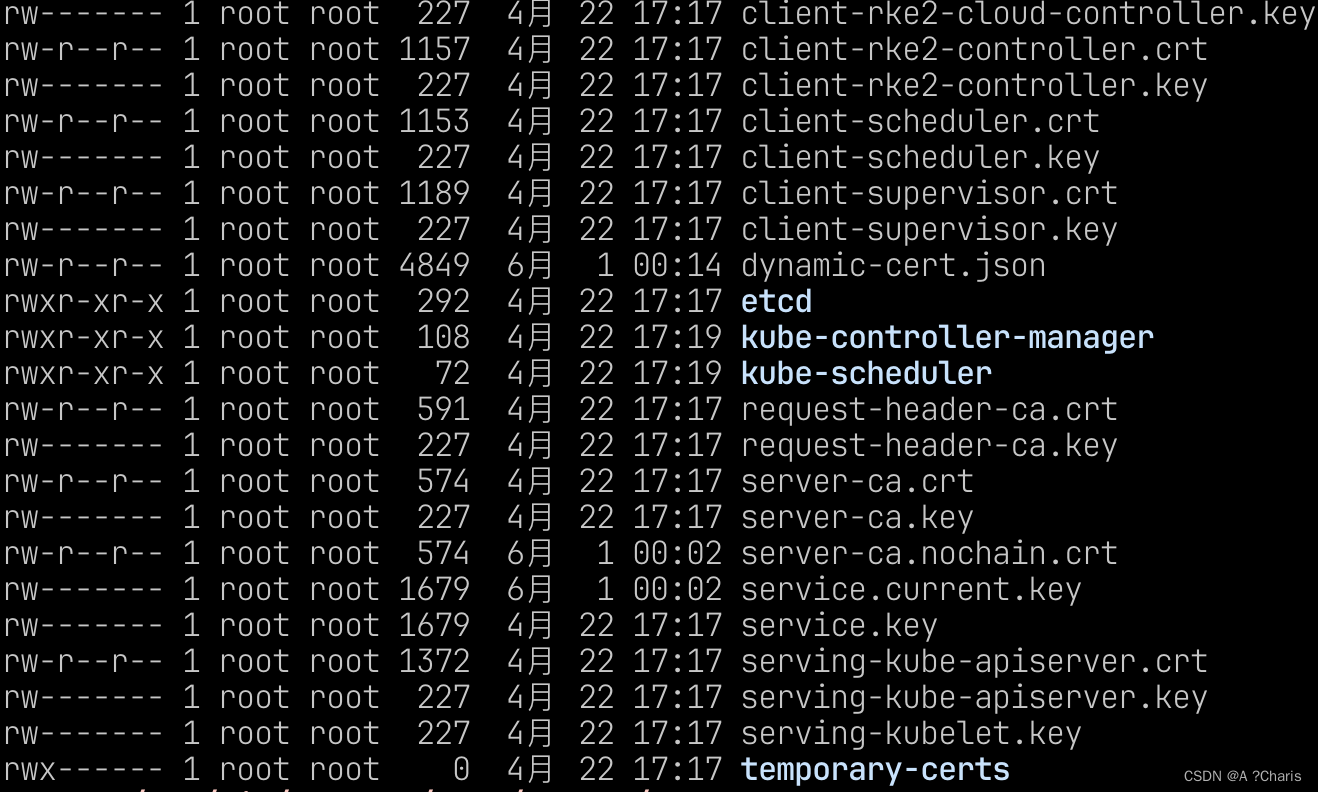
了解Kubernetes-RKE2的PKI以及证书存放位置
一、什么是PKI? 简称:证书基础设施。 可以方便理解为当你的集群有Server,Client架构,那么为了安全加密之间的通信,则需要使用证书进行交互,那么利用PKI架构可以安全加密组件之间的通信。 二、Kubernetes的PKI架构什…...

利用大语言模型进行事实匹配
论文地址:Automated Claim Matching with Large Language Models: Empowering Fact-Checkers in the Fight Against Misinformation | Companion Proceedings of the ACM on Web Conference 2024 WWW 2024 Automated Claim Matching with Large Language Models: Empowering F…...

【Stable Diffusion】(基础篇一)—— Stable Diffusion的安装
本系列笔记主要参考B站nenly同学的视频教程,传送门:B站第一套系统的AI绘画课!零基础学会Stable Diffusion,这绝对是你看过的最容易上手的AI绘画教程 | SD WebUI 保姆级攻略_哔哩哔哩_bilibili **Stable Diffusion(简称…...

维纳运动的概念
维纳运动(Wiener Process),也称为标准布朗运动,是一种重要的随机过程,广泛应用于数学、物理学和金融学等领域。它是一个连续时间的随机过程,具有一些特殊的性质,使其成为描述随机动态系统的经典…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
