Meta Llama 3 RMSNorm(Root Mean Square Layer Normalization)
Meta Llama 3 RMSNorm(Root Mean Square Layer Normalization)
flyfish
目录
- Meta Llama 3 RMSNorm(Root Mean Square Layer Normalization)
- 先看LayerNorm和BatchNorm
- 举个例子计算 LayerNorm
- RMSNorm 的整个计算过程
- 实际代码实现
- 结果
先看LayerNorm和BatchNorm
展示计算的方向

- axis=0 代表第一个轴,逐列处理数据。
- axis=1 代表第二个轴,逐行处理数据。在二维数组中,axis=-1 等同于 axis=1。
- axis=-1 代表最后一个轴。在二维数组中,axis=-1 等同于 axis=1,即最后一个轴。
在二维的情况 下,BatchNorm是按列算,LayerNorm按行算
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nnclass CustomLayerNorm:def __init__(self, eps=1e-5):self.eps = epsdef __call__(self, x):mean = np.mean(x, axis=-1, keepdims=True)std = np.std(x, axis=-1, keepdims=True)normalized = (x - mean) / (std + self.eps)return normalizedclass CustomBatchNorm:def __init__(self, eps=1e-5):self.eps = epsdef __call__(self, x):mean = np.mean(x, axis=0)std = np.std(x, axis=0)normalized = (x - mean) / (std + self.eps)return normalized# Original Data
data = np.array([[1.0, 2.0, 3.0],[4.0, 5.0, 6.0],[7.0, 8.0, 9.0]])# Apply Custom LayerNorm
custom_layer_norm = CustomLayerNorm()
custom_layer_norm_data = custom_layer_norm(data)# Apply Custom BatchNorm
custom_batch_norm = CustomBatchNorm()
custom_batch_norm_data = custom_batch_norm(data)# Apply PyTorch LayerNorm
data_tensor = torch.tensor(data, dtype=torch.float32)
layer_norm = nn.LayerNorm(data_tensor.size()[1:])
pytorch_layer_norm_data = layer_norm(data_tensor).detach().numpy()# Compare Custom and PyTorch LayerNorm
print("Original Data:\n", data)
print("Custom LayerNorm Data:\n", custom_layer_norm_data)
print("PyTorch LayerNorm Data:\n", pytorch_layer_norm_data)
Original Data:[[1. 2. 3.][4. 5. 6.][7. 8. 9.]]
Custom LayerNorm Data:[[-1.22472987 0. 1.22472987][-1.22472987 0. 1.22472987][-1.22472987 0. 1.22472987]]
PyTorch LayerNorm Data:[[-1.2247356 0. 1.2247356][-1.2247356 0. 1.2247356][-1.2247356 0. 1.2247356]]
举个例子计算 LayerNorm
具体步骤如下:
- 计算每行的均值:
- 对每一行,计算其均值。
- 第1行: mean = (1 + 2 + 3) / 3 = 2
- 第2行: mean = (4 + 5 + 6) / 3 = 5
- 第3行: mean = (7 + 8 + 9) / 3 = 8
- 计算每行的标准差:
- 对每一行,计算其标准差。
- 第1行: s t d = s q r t ( ( ( 1 − 2 ) 2 + ( 2 − 2 ) 2 + ( 3 − 2 ) 2 ) / 3 ) = s q r t ( ( 1 + 0 + 1 ) / 3 ) = s q r t ( 2 / 3 ) ≈ 0.8165 std = sqrt(((1-2)^2 + (2-2)^2 + (3-2)^2) / 3) = sqrt((1 + 0 + 1) / 3) = sqrt(2 / 3) ≈ 0.8165 std=sqrt(((1−2)2+(2−2)2+(3−2)2)/3)=sqrt((1+0+1)/3)=sqrt(2/3)≈0.8165
- 第2行: s t d = s q r t ( ( ( 4 − 5 ) 2 + ( 5 − 5 ) 2 + ( 6 − 5 ) 2 ) / 3 ) = s q r t ( ( 1 + 0 + 1 ) / 3 ) = s q r t ( 2 / 3 ) ≈ 0.8165 std = sqrt(((4-5)^2 + (5-5)^2 + (6-5)^2) / 3) = sqrt((1 + 0 + 1) / 3) = sqrt(2 / 3) ≈ 0.8165 std=sqrt(((4−5)2+(5−5)2+(6−5)2)/3)=sqrt((1+0+1)/3)=sqrt(2/3)≈0.8165
- 第3行: s t d = s q r t ( ( ( 7 − 8 ) 2 + ( 8 − 8 ) 2 + ( 9 − 8 ) 2 ) / 3 ) = s q r t ( ( 1 + 0 + 1 ) / 3 ) = s q r t ( 2 / 3 ) ≈ 0.8165 std = sqrt(((7-8)^2 + (8-8)^2 + (9-8)^2) / 3) = sqrt((1 + 0 + 1) / 3) = sqrt(2 / 3) ≈ 0.8165 std=sqrt(((7−8)2+(8−8)2+(9−8)2)/3)=sqrt((1+0+1)/3)=sqrt(2/3)≈0.8165
- 标准化每一行:
- 对每一行,使用均值和标准差进行标准化。公式为: ( x − m e a n ) / ( s t d + e p s ) (x - mean) / (std + eps) (x−mean)/(std+eps)。其中 eps 是一个小常数,防止除零,通常取值为 1e-5。
- 计算结果如下:
标准化公式: n o r m a l i z e d = ( x − m e a n ) / ( s t d + e p s ) normalized = (x - mean) / (std + eps) normalized=(x−mean)/(std+eps)
第1行:
[(1-2)/(0.8165+1e-5), (2-2)/(0.8165+1e-5), (3-2)/(0.8165+1e-5)]
= [-1.2247, 0, 1.2247]第2行:
[(4-5)/(0.8165+1e-5), (5-5)/(0.8165+1e-5), (6-5)/(0.8165+1e-5)]
= [-1.2247, 0, 1.2247]第3行:
[(7-8)/(0.8165+1e-5), (8-8)/(0.8165+1e-5), (9-8)/(0.8165+1e-5)]
= [-1.2247, 0, 1.2247]
最终标准化结果矩阵为:
[[-1.2247, 0, 1.2247][-1.2247, 0, 1.2247][-1.2247, 0, 1.2247]]
RMSNorm 的整个计算过程
Meta Llama 3 使用了RMSNorm
假设我们有以下 2D 输入张量 X X X(为了简单起见,我们假设这个张量有 2 行 3 列):
[ 1 2 3 4 5 6 ] \begin{bmatrix}1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} [142536]
RMSNorm 的计算过程如下:
- 计算每行的均方根 (RMS):
首先,对于每一行,我们计算该行元素的平方和的均值,然后取其平方根。
对于第 1 行:
RMS row1 = 1 2 + 2 2 + 3 2 3 = 1 + 4 + 9 3 = 4.67 ≈ 2.16 \text{RMS}_{\text{row1}} = \sqrt{\frac{1^2 + 2^2 + 3^2}{3}} = \sqrt{\frac{1 + 4 + 9}{3}} = \sqrt{4.67} \approx 2.16 RMSrow1=312+22+32=31+4+9=4.67≈2.16
对于第 2 行:
RMS row2 = 4 2 + 5 2 + 6 2 3 = 16 + 25 + 36 3 = 25.67 ≈ 5.07 \text{RMS}_{\text{row2}} = \sqrt{\frac{4^2 + 5^2 + 6^2}{3}} = \sqrt{\frac{16 + 25 + 36}{3}} = \sqrt{25.67} \approx 5.07 RMSrow2=342+52+62=316+25+36=25.67≈5.07 - 使用均方根对输入进行归一化:
将每行的元素除以该行的 RMS 值。这里的 epsilon 用于防止除以零的问题,我们假设 ϵ = 1 e − 6 \epsilon = 1e-6 ϵ=1e−6。
对于第 1 行: Normed row1 = [ 1 2.16 + ϵ 2 2.16 + ϵ 3 2.16 + ϵ ] ≈ [ 0.462 0.925 1.387 ] \text{Normed}_{\text{row1}} = \begin{bmatrix} \frac{1}{2.16 + \epsilon} & \frac{2}{2.16 + \epsilon} & \frac{3}{2.16 + \epsilon} \end{bmatrix} \approx \begin{bmatrix} 0.462 & 0.925 & 1.387 \end{bmatrix} Normedrow1=[2.16+ϵ12.16+ϵ22.16+ϵ3]≈[0.4620.9251.387]
对于第 2 行: Normed row2 = [ 4 5.07 + ϵ 5 5.07 + ϵ 6 5.07 + ϵ ] ≈ [ 0.789 0.986 1.183 ] \text{Normed}_{\text{row2}} = \begin{bmatrix} \frac{4}{5.07 + \epsilon} & \frac{5}{5.07 + \epsilon} & \frac{6}{5.07 + \epsilon} \end{bmatrix} \approx \begin{bmatrix} 0.789 & 0.986 & 1.183 \end{bmatrix} Normedrow2=[5.07+ϵ45.07+ϵ55.07+ϵ6]≈[0.7890.9861.183] - 应用可学习的缩放参数:
假设权重参数 weight \text{weight} weight 为一个向量 [ 1 , 1 , 1 ] [1, 1, 1] [1,1,1],表示每个元素的缩放因子。对于第 1 行: Output row1 = [ 0.462 ⋅ 1 0.925 ⋅ 1 1.387 ⋅ 1 ] = [ 0.462 0.925 1.387 ] \text{Output}_{\text{row1}} = \begin{bmatrix} 0.462 \cdot 1 & 0.925 \cdot 1 & 1.387 \cdot 1 \end{bmatrix} = \begin{bmatrix} 0.462 & 0.925 & 1.387 \end{bmatrix} Outputrow1=[0.462⋅10.925⋅11.387⋅1]=[0.4620.9251.387]对于第 2 行: Output row2 = [ 0.789 ⋅ 1 0.986 ⋅ 1 1.183 ⋅ 1 ] = [ 0.789 0.986 1.183 ] \text{Output}_{\text{row2}} = \begin{bmatrix} 0.789 \cdot 1 & 0.986 \cdot 1 & 1.183 \cdot 1 \end{bmatrix} = \begin{bmatrix} 0.789 & 0.986 & 1.183 \end{bmatrix} Outputrow2=[0.789⋅10.986⋅11.183⋅1]=[0.7890.9861.183]
实际代码实现
以下是使用 PyTorch 实现上述步骤的代码示例:
import torch
import torch.nn as nnclass RMSNorm(nn.Module):def __init__(self, dim: int, eps: float = 1e-6):super().__init__()self.eps = epsself.weight = nn.Parameter(torch.ones(dim))def _norm(self, x):return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)def forward(self, x):output = self._norm(x.float()).type_as(x)return output * self.weight# 示例数据
data = torch.tensor([[1.0, 2.0, 3.0],[4.0, 5.0, 6.0]])# 实例化 RMSNorm 层
rms_norm = RMSNorm(dim=data.size(-1))# 计算归一化后的输出
normalized_data = rms_norm(data)print("Original Data:\n", data)
print("RMSNorm Normalized Data:\n", normalized_data)
结果
运行上述代码后,我们将得到归一化后的数据:
tensor([[1., 2., 3.],[4., 5., 6.]])
RMSNorm Normalized Data:tensor([[0.4629, 0.9258, 1.3887],[0.7895, 0.9869, 1.1843]], grad_fn=<MulBackward0>)
相关文章:

Meta Llama 3 RMSNorm(Root Mean Square Layer Normalization)
Meta Llama 3 RMSNorm(Root Mean Square Layer Normalization) flyfish 目录 Meta Llama 3 RMSNorm(Root Mean Square Layer Normalization)先看LayerNorm和BatchNorm举个例子计算 LayerNormRMSNorm 的整个计算过程实际代码实现结…...

MySQL-6、单表访问方法
前言 前面介绍了MySQL表空间相关的内容。包括区、段、碎片区,还有一些不同的页类型的作用。 (如果没有看前面五篇文章,不建议看此篇文章) 传送门: MySQL-1、InnoDB行格式 MySQL-2、InnoDB数据页 MySQL-3、索引 M…...

C语言实现三角波生成
C语言实现三角波生成 #include <stdio.h>#define SAMPLE_RATE 10000 // 采样率10kHz=10000Hz 对应100us=0.1ms #define UP_TIME 12.5 //上升时间12.5ms #...
WPF国际化的最佳实践
WPF国际化的最佳实践 1.创建项目资源文件 如果你的项目没有Properties文件夹和Resources.resx文件,可以通过右键项目-资源-常规-添加创建或打开程序集资源 2.添加国际化字符串 打开Resources.resx文件,添加需要翻译的文本字符,并将访问修…...
ctfshow web
【nl】难了 <?php show_source(__FILE__); error_reporting(0); if(strlen($_GET[1])<4){echo shell_exec($_GET[1]); } else{echo "hack!!!"; } ?> //by Firebasky //by Firebasky ?1>nl //先写个文件 ?1*>b //这样子会把所有文件名写在b里…...
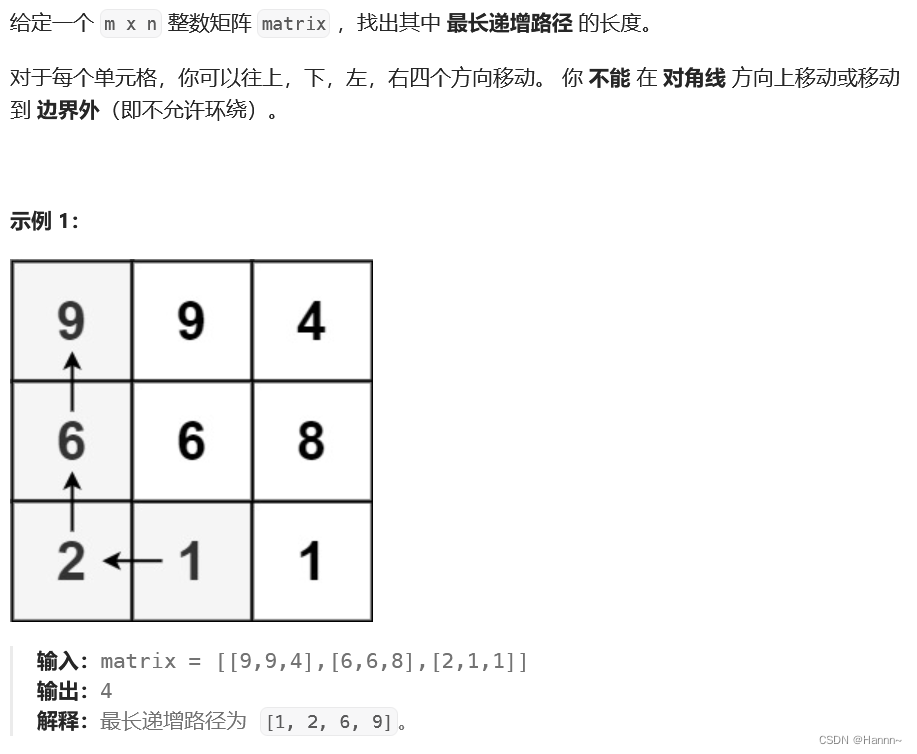
【力扣】矩阵中的最长递增路径
一、题目描述 二、解题思路 1、先求出以矩阵中的每个单元格为起点的最长递增路径 题目中说,对于每个单元格,你可以往上,下,左,右四个方向移动。那么以一个单元格为起点的最长递增路径就是:从该单元格往上…...
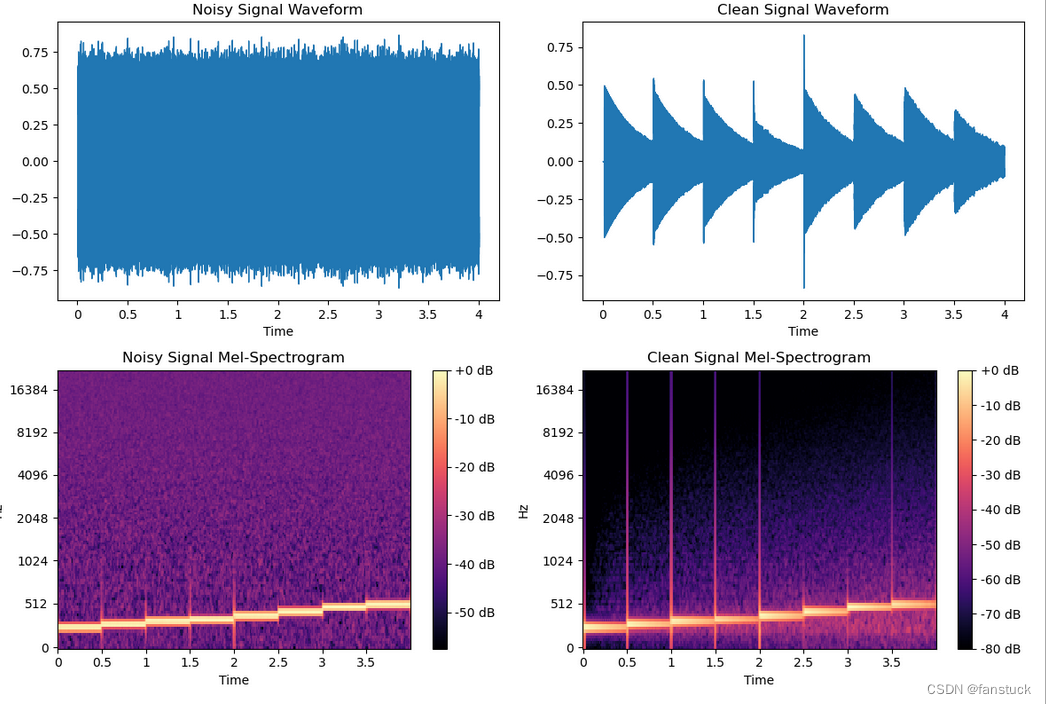
语音深度鉴伪识别项目实战:基于深度学习的语音深度鉴伪识别算法模型(二)音频数据预处理及去噪算法+Python源码应用
前言 深度学习技术在当今技术市场上面尚有余力和开发空间的,主流落地领域主要有:视觉,听觉,AIGC这三大板块。 目前视觉板块的框架和主流技术在我上一篇基于Yolov7-LPRNet的动态车牌目标识别算法模型已有较为详细的解说。与AIGC相…...

网络原理——http/https ---http(1)
T04BF 👋专栏: 算法|JAVA|MySQL|C语言 🫵 今天你敲代码了吗 网络原理 HTTP/HTTPS HTTP,全称为"超文本传输协议" HTTP 诞⽣与1991年. ⽬前已经发展为最主流使⽤的⼀种应⽤层协议. 实际上,HTTP最新已经发展到 3.0 但是当前行业中主要使用的HT…...
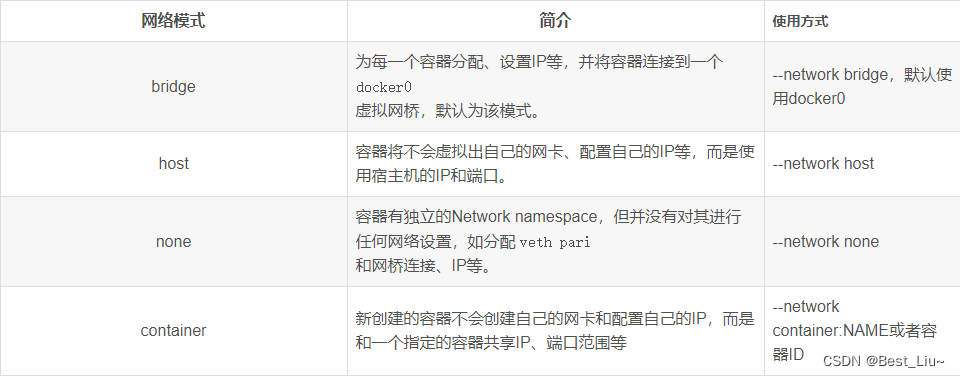
Docker安装、使用,容器化部署springboot项目
目录 一、使用官方安装脚本自动安装 二、Docker离线安装 1. 下载安装包 2. 解压 3.创建docker.service文件 4. 启动docker 三、docker常用命令 1. docker常用命令 2. docker镜像命令 3. docker镜像下载 4.docker镜像push到仓库 5. docker操作容器 6.docker …...
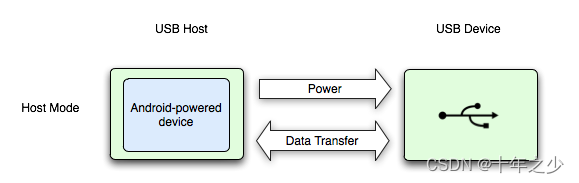
USB主机模式——Android
理论 摘自:USB 主机和配件概览 | Connectivity | Android Developers (google.cn) Android 通过 USB 配件和 USB 主机两种模式支持各种 USB 外围设备和 Android USB 配件(实现 Android 配件协议的硬件)。 在 USB 主机模式下࿰…...

240520Scala笔记
240520Scala笔记 第 7 章 集合 7.1 集合1 数组Array 集合(Test01_ImmutableArray): package chapter07 object Test01_ImmutableArray {def main(args: Array[String]): Unit {// 1. 创建数组val arr: Array[Int] new Array[Int](5)// 另一种创建方式val arr2 Array(…...
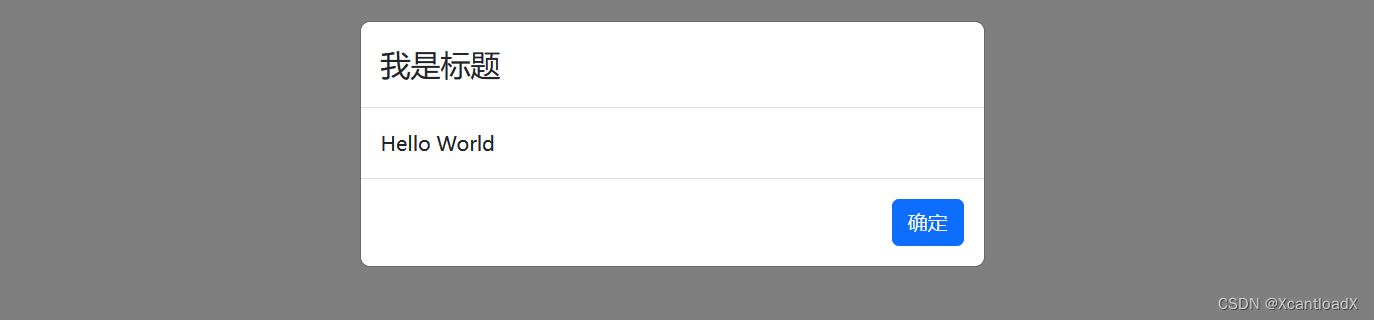
【React】封装一个好用方便的消息框(Hooks Bootstrap 实践)
引言 以 Bootstrap 为例,使用模态框编写一个简单的消息框: import { useState } from "react"; import { Modal } from "react-bootstrap"; import Button from "react-bootstrap/Button"; import bootstrap/dist/css/b…...
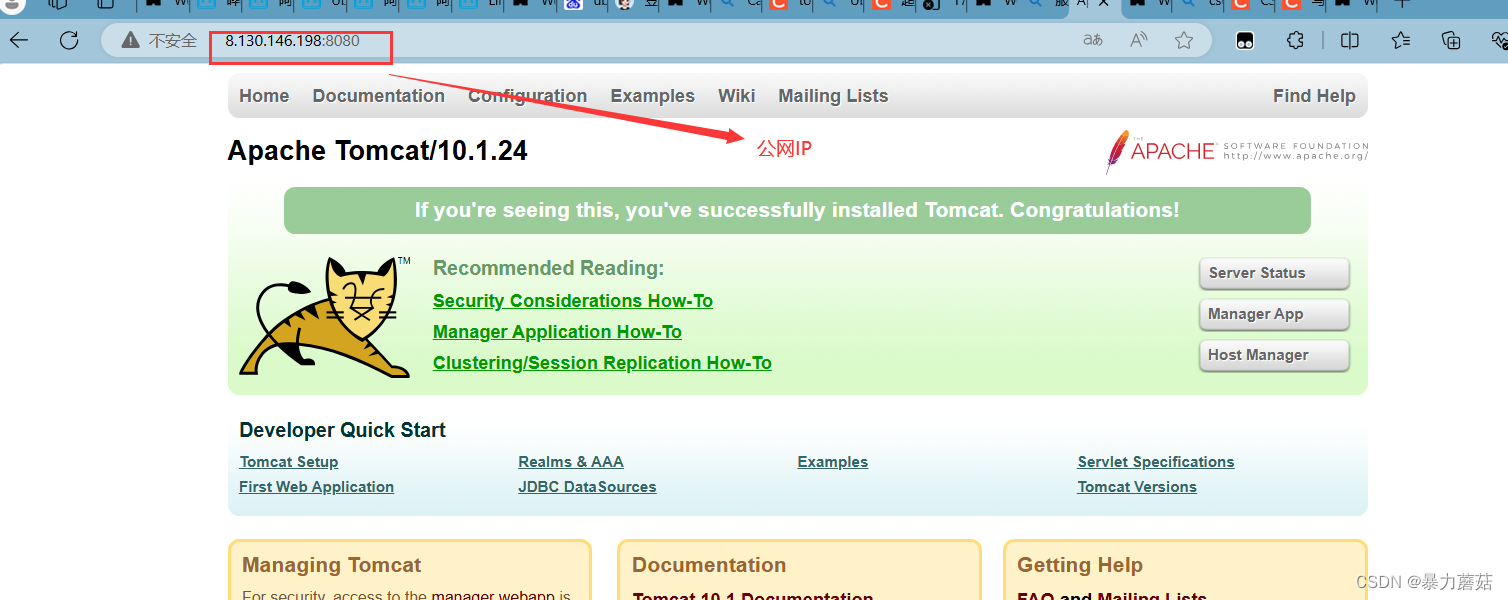
tomcat10部署踩坑记录-公网IP和服务器系统IP搞混
1. 服务器基本条件 使用的阿里云服务器,镜像系统是Ubuntu16.04java version “17.0.11” 2024-04-16 LTS装的是tomcat10.1.24阿里云服务器安全组放行了:8080端口 服务器防火墙关闭: 监听情况和下图一样: tomcat正常启动ÿ…...

探索Sass:Web开发的强大工具
在现代Web开发中,CSS(层叠样式表)作为前端样式设计的核心技术,已经发展得非常成熟。然而,随着Web应用的复杂性不断增加,传统的CSS书写方式逐渐暴露出一些不足之处,如代码冗长、难以维护、缺乏编程功能等。为了解决这些问题,Sass(Syntactically Awesome Stylesheets)应…...

vue组件之间的通信方式有哪些
在开发过程中,数据传输是一个核心的知识点,掌握了数据传输,相当于掌握了80%的内容。 Vue.js 提供了多种组件间的通信方式,这些方式适应不同的场景和需求。下面是4种常见的通信方式: 1. Props & Events (父子组件通…...
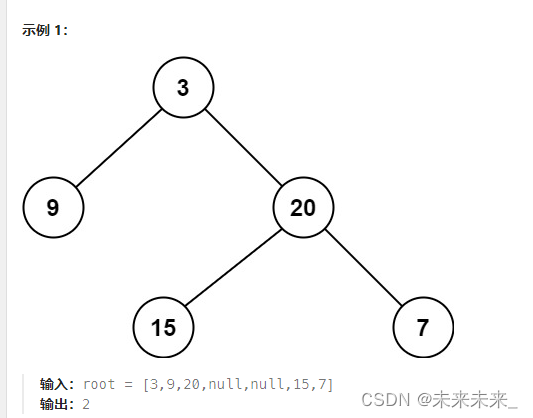
111、二叉树的最小深度
给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 题解:找出最小深度也就是找出根节点相对所有叶子结点的最小高度,在这也表明了根节点的高度是变化的,相对不同的叶子结点有不同的高度。…...
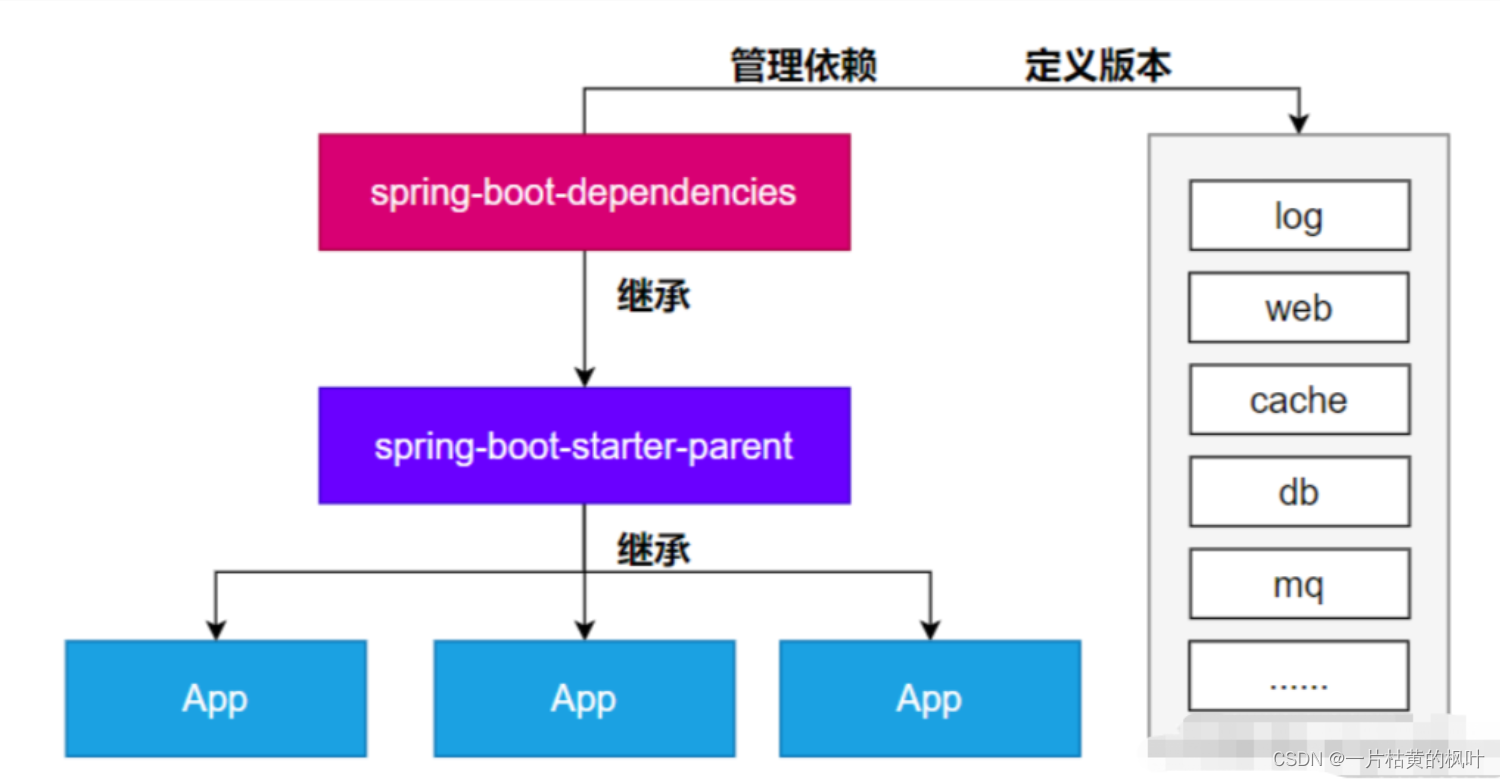
SpringBoot3依赖管理,自动配置
文章目录 1. 项目新建2. 相关pom依赖3. 依赖管理机制导入 starter 所有相关依赖都会导入进来为什么版本号都不用写?如何自定义版本号第三方的jar包 4. 自动配置机制5. 核心注解 1. 项目新建 直接建Maven项目通过官方提供的Spring Initializr项目创建 2. 相关pom依…...

音视频开发17 FFmpeg 音频解码- 将 aac 解码成 pcm
这一节,接 音视频开发12 FFmpeg 解复用详情分析,前面我们已经对一个 MP4文件,或者 FLV文件,或者TS文件进行了 解复用,解出来的 视频是H264,音频是AAC,那么接下来就要对H264和AAC进行处理,这一节…...
)
vue2中封装图片上传获取方法类(针对后端返回的数据不是图片链接,只是图片编号)
在Vue 2中实现商品列表中带有图片编号,并将返回的图片插入到商品列表中,可以通过以下步骤完成: 在Vue组件的data函数中定义商品列表和图片URL数组。 创建一个方法来获取每个商品的图片URL。 使用v-for指令在模板中遍历商品列表,并…...
this指针和静态成员)
【C++面向对象编程】(二)this指针和静态成员
文章目录 this指针和静态成员this指针静态成员 this指针和静态成员 this指针 C中类的成员变量和成员函数的存储方式有所不同: 成员变量:对象的成员变量直接作为对象的一部分存储在内存中。成员函数:成员函数(非静态成员函数&am…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
