【力扣】矩阵中的最长递增路径
一、题目描述
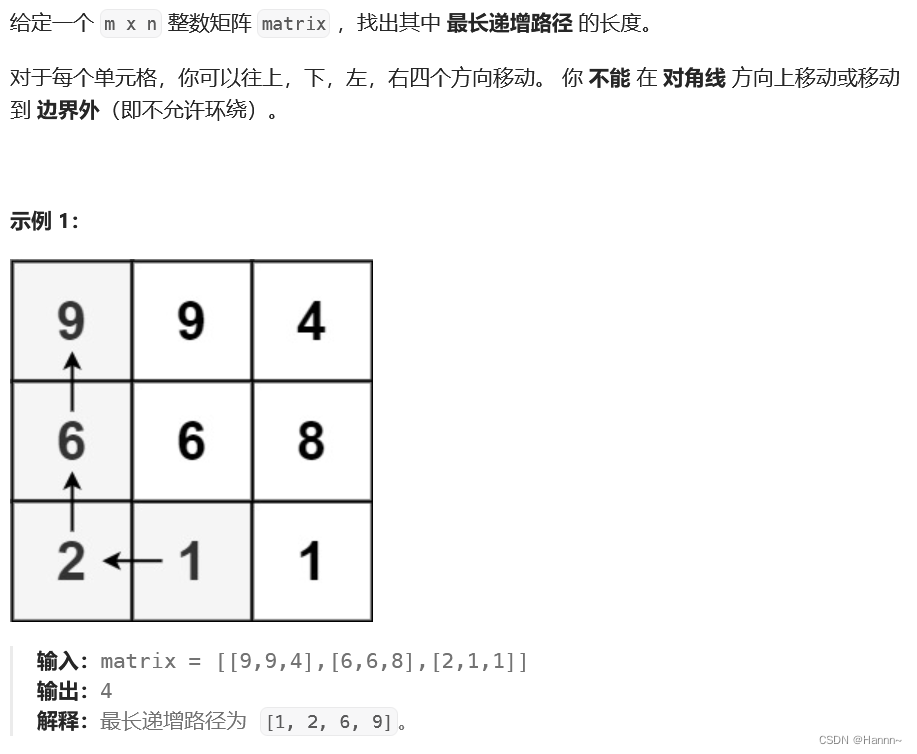
二、解题思路
1、先求出以矩阵中的每个单元格为起点的最长递增路径
题目中说,对于每个单元格,你可以往上,下,左,右四个方向移动。那么以一个单元格为起点的最长递增路径就是:从该单元格往上,下,左,右四个方向走的四条递增路径中的最大值(即最长的一条递增路径)。
2、在求出的所有最长递增路径中找最大值
因为题目是求矩阵中的最长递增路径,所以要在求出的所有最长递增路径中找最大值。
3、使用“记忆化搜索”(递归+“备忘录” )来解决该题。
三、 代码
class Solution {int m, n;//遍历上、下、左、右四个方向所需的数组int[] dx = {0,0,1,-1};int[] dy = {1,-1,0,0};int[][] memo; //备忘录public int longestIncreasingPath(int[][] matrix) {m = matrix.length;n = matrix[0].length;memo = new int[m][n];//求所有的最长递增路径中的最大值int ret = 0;for(int i = 0; i < m; i++) {for(int j = 0; j < n; j++) {ret = Math.max(ret,dfs(i, j, matrix));}}return ret;}//递归函数//求出以矩阵中的每个单元格为起点的最长递增路径(上下左右四个方向中的最大值)public int dfs(int i, int j, int[][] matrix) {if(memo[i][j] != 0) {return memo[i][j];}int ret = 1;for(int k = 0; k < 4; k++) {int x = i + dx[k];int y = j + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j]) {ret = Math.max(ret, dfs(x,y,matrix)+1);}}memo[i][j] = ret;return ret;}
}
相关文章:

【力扣】矩阵中的最长递增路径
一、题目描述 二、解题思路 1、先求出以矩阵中的每个单元格为起点的最长递增路径 题目中说,对于每个单元格,你可以往上,下,左,右四个方向移动。那么以一个单元格为起点的最长递增路径就是:从该单元格往上…...
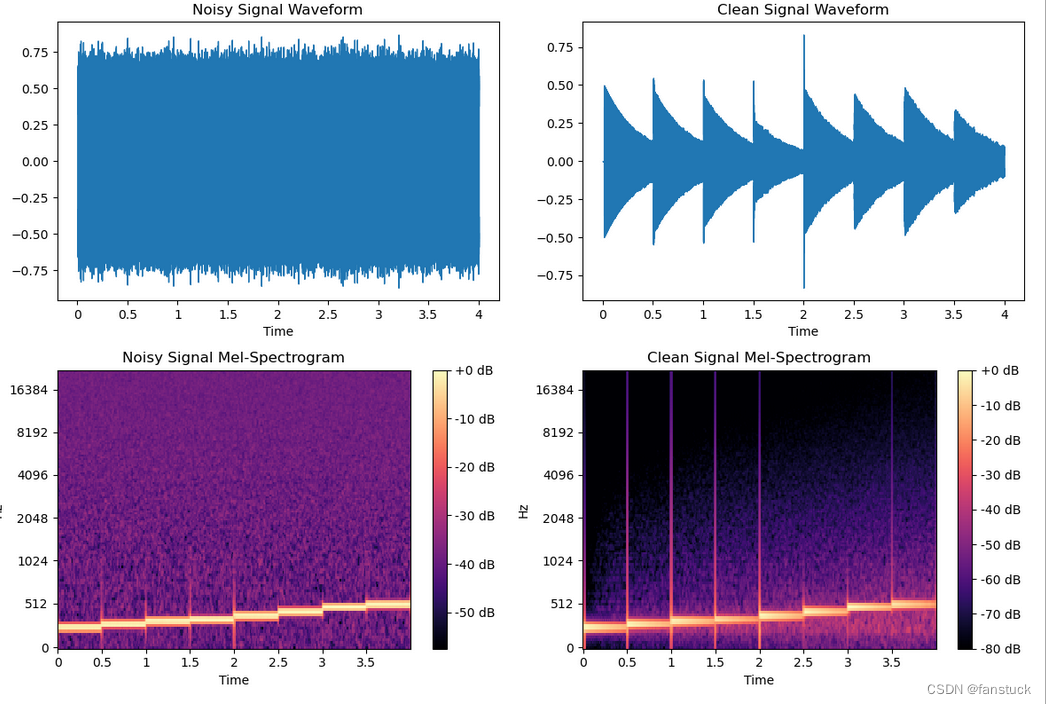
语音深度鉴伪识别项目实战:基于深度学习的语音深度鉴伪识别算法模型(二)音频数据预处理及去噪算法+Python源码应用
前言 深度学习技术在当今技术市场上面尚有余力和开发空间的,主流落地领域主要有:视觉,听觉,AIGC这三大板块。 目前视觉板块的框架和主流技术在我上一篇基于Yolov7-LPRNet的动态车牌目标识别算法模型已有较为详细的解说。与AIGC相…...

网络原理——http/https ---http(1)
T04BF 👋专栏: 算法|JAVA|MySQL|C语言 🫵 今天你敲代码了吗 网络原理 HTTP/HTTPS HTTP,全称为"超文本传输协议" HTTP 诞⽣与1991年. ⽬前已经发展为最主流使⽤的⼀种应⽤层协议. 实际上,HTTP最新已经发展到 3.0 但是当前行业中主要使用的HT…...
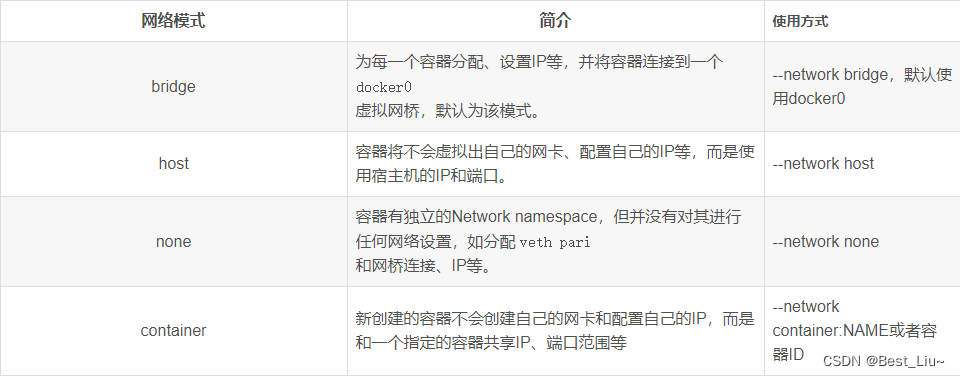
Docker安装、使用,容器化部署springboot项目
目录 一、使用官方安装脚本自动安装 二、Docker离线安装 1. 下载安装包 2. 解压 3.创建docker.service文件 4. 启动docker 三、docker常用命令 1. docker常用命令 2. docker镜像命令 3. docker镜像下载 4.docker镜像push到仓库 5. docker操作容器 6.docker …...
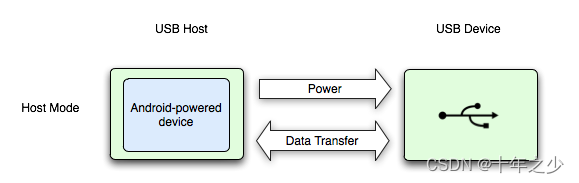
USB主机模式——Android
理论 摘自:USB 主机和配件概览 | Connectivity | Android Developers (google.cn) Android 通过 USB 配件和 USB 主机两种模式支持各种 USB 外围设备和 Android USB 配件(实现 Android 配件协议的硬件)。 在 USB 主机模式下࿰…...

240520Scala笔记
240520Scala笔记 第 7 章 集合 7.1 集合1 数组Array 集合(Test01_ImmutableArray): package chapter07 object Test01_ImmutableArray {def main(args: Array[String]): Unit {// 1. 创建数组val arr: Array[Int] new Array[Int](5)// 另一种创建方式val arr2 Array(…...
【React】封装一个好用方便的消息框(Hooks Bootstrap 实践)
引言 以 Bootstrap 为例,使用模态框编写一个简单的消息框: import { useState } from "react"; import { Modal } from "react-bootstrap"; import Button from "react-bootstrap/Button"; import bootstrap/dist/css/b…...
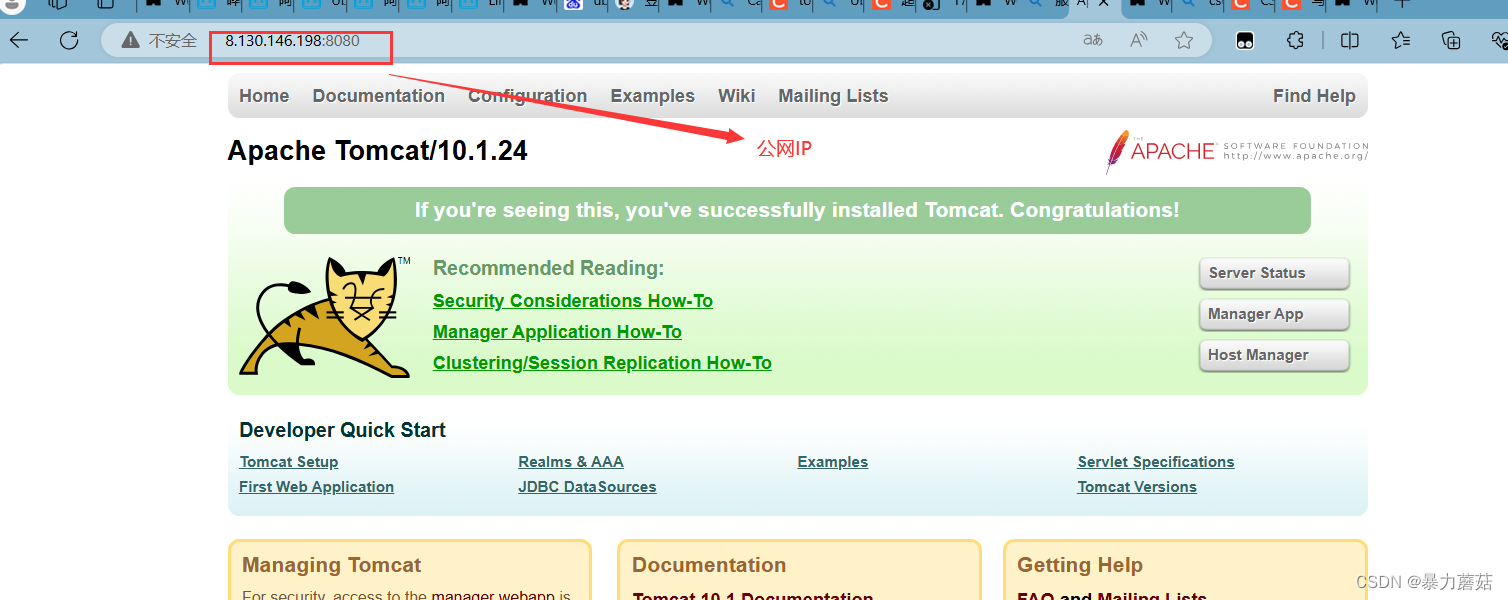
tomcat10部署踩坑记录-公网IP和服务器系统IP搞混
1. 服务器基本条件 使用的阿里云服务器,镜像系统是Ubuntu16.04java version “17.0.11” 2024-04-16 LTS装的是tomcat10.1.24阿里云服务器安全组放行了:8080端口 服务器防火墙关闭: 监听情况和下图一样: tomcat正常启动ÿ…...

探索Sass:Web开发的强大工具
在现代Web开发中,CSS(层叠样式表)作为前端样式设计的核心技术,已经发展得非常成熟。然而,随着Web应用的复杂性不断增加,传统的CSS书写方式逐渐暴露出一些不足之处,如代码冗长、难以维护、缺乏编程功能等。为了解决这些问题,Sass(Syntactically Awesome Stylesheets)应…...

vue组件之间的通信方式有哪些
在开发过程中,数据传输是一个核心的知识点,掌握了数据传输,相当于掌握了80%的内容。 Vue.js 提供了多种组件间的通信方式,这些方式适应不同的场景和需求。下面是4种常见的通信方式: 1. Props & Events (父子组件通…...
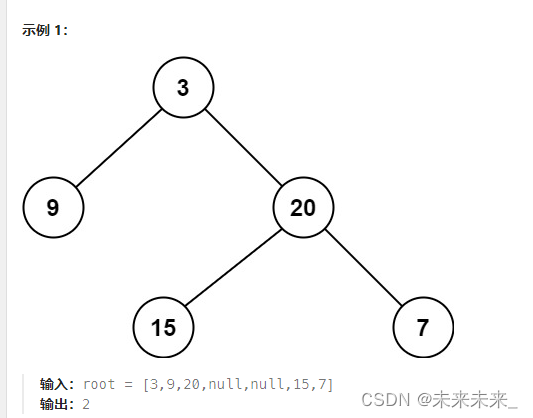
111、二叉树的最小深度
给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 题解:找出最小深度也就是找出根节点相对所有叶子结点的最小高度,在这也表明了根节点的高度是变化的,相对不同的叶子结点有不同的高度。…...
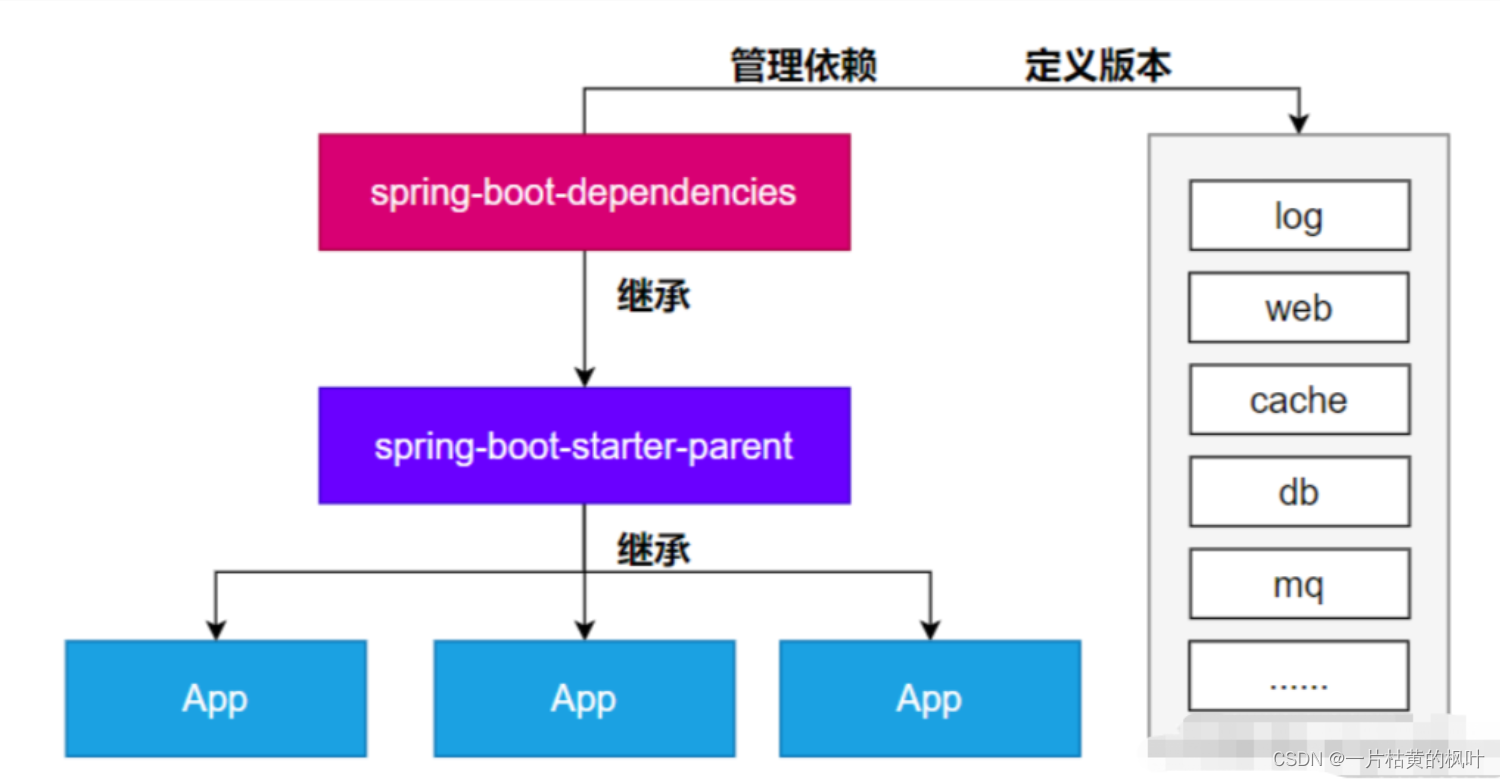
SpringBoot3依赖管理,自动配置
文章目录 1. 项目新建2. 相关pom依赖3. 依赖管理机制导入 starter 所有相关依赖都会导入进来为什么版本号都不用写?如何自定义版本号第三方的jar包 4. 自动配置机制5. 核心注解 1. 项目新建 直接建Maven项目通过官方提供的Spring Initializr项目创建 2. 相关pom依…...

音视频开发17 FFmpeg 音频解码- 将 aac 解码成 pcm
这一节,接 音视频开发12 FFmpeg 解复用详情分析,前面我们已经对一个 MP4文件,或者 FLV文件,或者TS文件进行了 解复用,解出来的 视频是H264,音频是AAC,那么接下来就要对H264和AAC进行处理,这一节…...
)
vue2中封装图片上传获取方法类(针对后端返回的数据不是图片链接,只是图片编号)
在Vue 2中实现商品列表中带有图片编号,并将返回的图片插入到商品列表中,可以通过以下步骤完成: 在Vue组件的data函数中定义商品列表和图片URL数组。 创建一个方法来获取每个商品的图片URL。 使用v-for指令在模板中遍历商品列表,并…...
this指针和静态成员)
【C++面向对象编程】(二)this指针和静态成员
文章目录 this指针和静态成员this指针静态成员 this指针和静态成员 this指针 C中类的成员变量和成员函数的存储方式有所不同: 成员变量:对象的成员变量直接作为对象的一部分存储在内存中。成员函数:成员函数(非静态成员函数&am…...
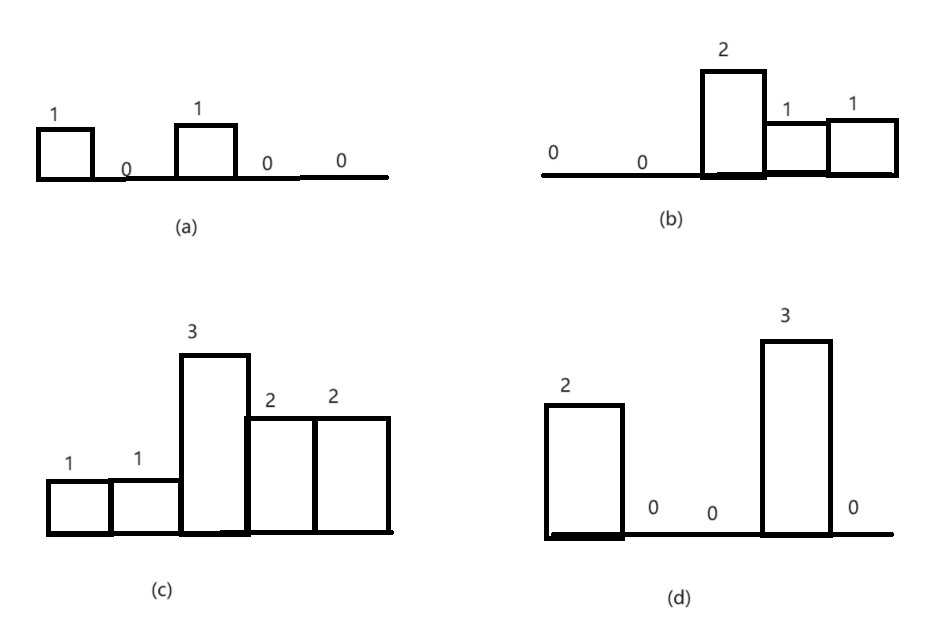
最大矩形问题
柱状图中最大的矩形 题目 分析 矩形的面积等于宽乘以高,因此只要能确定每个矩形的宽和高,就能计算它的面积。如果直方图中一个矩形从下标为 i 的柱子开始,到下标为 j 的柱子结束,那么这两根柱子之间的矩形(含两端的柱…...

LeetCode62不同路径
题目描述 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。问总共有多少条不同的路径? …...
GNU Radio实现OFDM Radar
文章目录 前言一、GNU Radio Radar Toolbox编译及安装二、ofdm radar 原理讲解三、GNU Radio 实现 OFDM Radar1、官方提供的 grc①、grc 图②、运行结果 2、修改后的便于后续可实现探测和通信的 grc①、grc 图②、运行结果 四、资源自取 前言 本文使用 GNU Radio 搭建 OFDM Ra…...

东方博宜1760 - 整理抽屉
题目描述 期末考试即将来临,小T由于同时肩负了学习、竞赛、班团活动等多方面的任务,一直没有时间好好整理他的课桌抽屉,为了更好地复习,小T首先要把课桌抽屉里的书分类整理好。 小T的抽屉里堆着 N 本书,每本书的封面上…...
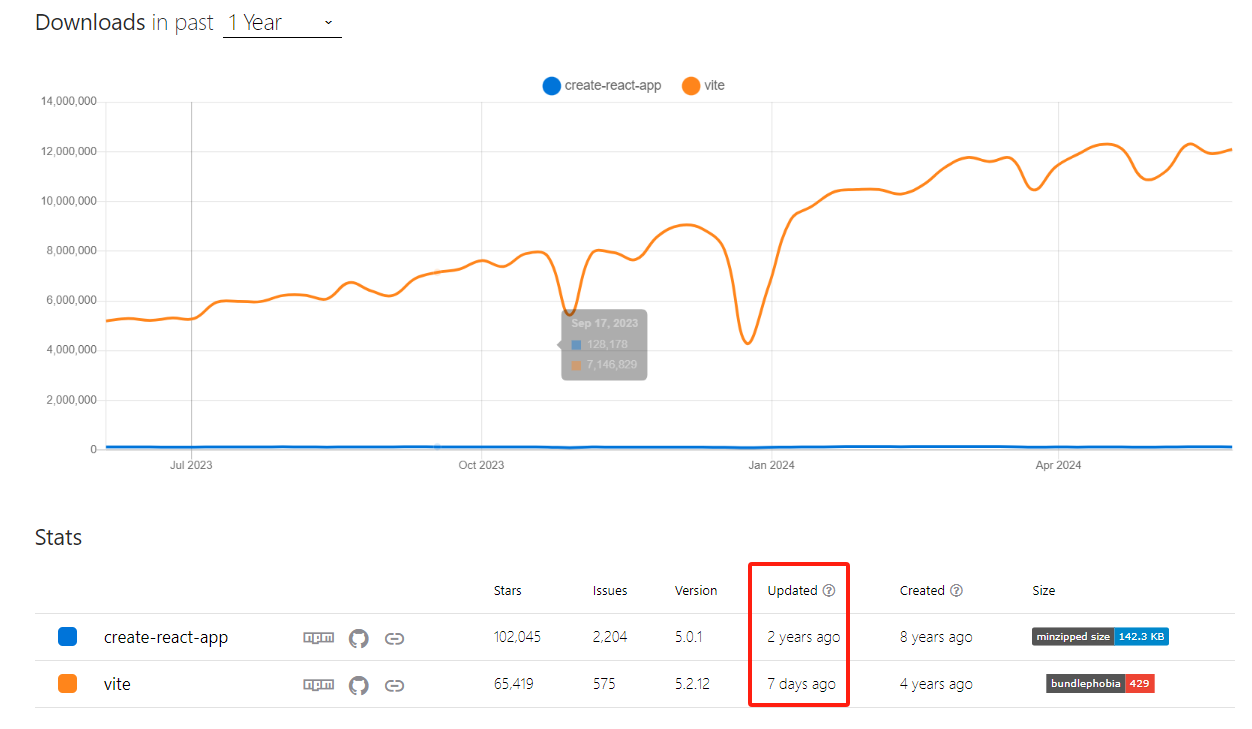
react快速开始(四)-之Vite 还是 (Create React App) CRA? 用Vite创建项目
文章目录 react快速开始(四)-之Vite 还是 (Create React App) CRA? 用Vite创建项目背景Vite 和 (Create React App) CRAVite?Vite 是否支持 TypeScript? 用Vite创建react项目参考 react快速开始(四)-之Vite 还是 (Create React App) CRA? 用Vite创建项…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
