最大矩形问题
柱状图中最大的矩形
题目



分析
矩形的面积等于宽乘以高,因此只要能确定每个矩形的宽和高,就能计算它的面积。如果直方图中一个矩形从下标为 i 的柱子开始,到下标为 j 的柱子结束,那么这两根柱子之间的矩形(含两端的柱子)的宽是 j-i+1,矩形的高就是两根柱子之间的所有柱子最矮的高度。
暴力解法(不可取)
如果能逐一找出直方图中所有矩形并比较它们的面积,就能够得到最大矩形的面积。方法为:采用嵌套的二重循环遍历所有矩形,并比较他们的面积。该种方法的时间复杂度为O(N^2),根据题目所给的提示可知,这种方法不能解决本题,会超时。
代码为
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int n=heights.size();int maxarea=0;for(int i=0;i<n;i++){int minheight=heights[i];for(int j=i;j<n;j++){minheight=min(minheight,heights[j]);int area=minheight*(j-i+1);maxarea=max(maxarea,area);}}return maxarea;}
};分治法(本题不可取)
仔细观察直方图可以发现,这个直方图的最大矩形有3中可能:
第一种:矩形通过直方图中最矮的柱子;
第二种:矩形的起始柱子和终止柱子都在直方图中最矮柱子的左侧;
第三种:矩形的起始柱子和终止柱子都在直方图中最矮柱子的右侧。
第二种和第三种从本质上来说和求整个直方图的最大矩形面积是同一个问题,可以用递归函数解决。
代码为:
class Solution {
public:int largestRectangleArea(vector<int>& heights) {return helper(heights,0,heights.size()-1);}int helper(vector<int>& heights,int start,int end){if(start>end) return 0;else if(start==end) return heights[start];else{int minindex=start;for(int i=start+1;i<=end;i++){if(heights[i]<heights[minindex])minindex=i;}int area=(end-start+1)*heights[minindex];int left=helper(heights,start,minindex-1);int right=helper(heights,minindex+1,end);return max(area,max(left,right));}}
};单调栈法(可取)
下面介绍一种非常高效,巧妙的解法。这种解法用一个栈保存直方图的柱子,并且在栈中的柱子的高度是递增排序的。为了方便计算矩阵的高度,栈中保存的是柱子在数组中的下标,可以根据下标得到柱子的高度。
这种解法的基本思想是确保保存在栈中的直方图的柱子的敢赌是递增排序的。假设从左到右逐一扫描数组中的每根柱子,如果当前柱子的高度大于位于栈顶柱子的高度,那么将该柱子的下标入栈;否则,将位于栈顶的柱子的下标出栈,并且计算以位于栈顶的柱子为顶的最大矩形的面积。【注意:此时出栈须满足:栈不为空并且栈顶柱子的高度大于等于当前柱子的高度】
以某根柱子为顶的最大矩形,一定是从该柱子向两侧眼神知道遇到比它矮的柱子,这个最大矩形的高是该柱子的高,最大矩形的宽是两侧比它矮的柱子中间的间隔。
如果当前扫描到的柱子的高小于位于栈顶柱子的高,那么将位于栈顶的柱子的下标出栈,并且计算以位于栈顶的柱子为顶的最大矩形的面积。由于保存在栈中的柱子的高度是递增排序的,因此栈中位于栈顶前面的一根柱子一定比位于栈顶的柱子矮,于是很容易就能找到位于栈顶的柱子两侧比它矮的柱子。
当计算以当前柱子为顶的最大矩形的面积时,如果栈中没有柱子,那么意味着它左侧的柱子都比它高,因此可以想象在下标为 -1 的位置有一根比它矮的柱子。
当扫描数组中所以柱子之后,栈中可能仍然剩余一些柱子。因此,需要注意将这些柱子的下标出栈并计算以它们为顶的最大矩形的面积。
在扫描完数组中所有的柱子之后,当计算以当前柱子为顶的最大矩形的面积时,说明它的右侧没有比它矮的柱子,如果一根柱子的右侧有比它矮的柱子,那么当扫描到右侧较矮柱子的时候他就已经出栈了。因此,可以想象下标为数组长度的位置有一根比它矮的柱子。
由于已经计算了以每根柱子为顶的最大矩形面积,因此比较这些矩形的面积就能得到脂肪图中的最大矩形面积。
代码为
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int n=heights.size();stack<int> st;st.push(-1);int maxarea=0;for(int i=0;i<n;i++){while(st.top()!=-1 && heights[st.top()]>=heights[i]){int height=heights[st.top()];st.pop();int width=i-st.top()-1;maxarea=max(maxarea,height*width);}st.push(i);}while(st.top() != -1){int height=heights[st.top()];st.pop();int width=n-st.top()-1;maxarea=max(maxarea,height*width);}return maxarea;}
};最大矩形
题目



分析
上一道题是关于最大矩形的,这道题也是关于最大矩形的,他们之间有没有某种联系?如果能从矩阵中找出直方图,那么就能通过计算直方图中的最大矩形面积来计算矩阵中的最大矩形面积。
直方图是由排列在同一基线上的相邻柱子组成的图形,由于题目要求矩形中只包含数字1,因此将矩阵中上下相邻的值为1的各自看成直方图中的柱子,如果分别以矩阵的每行为基线,就可以得到若干行由数字1的格子组成的直方图。如下图所示:
 对应的直方图如下:
对应的直方图如下:
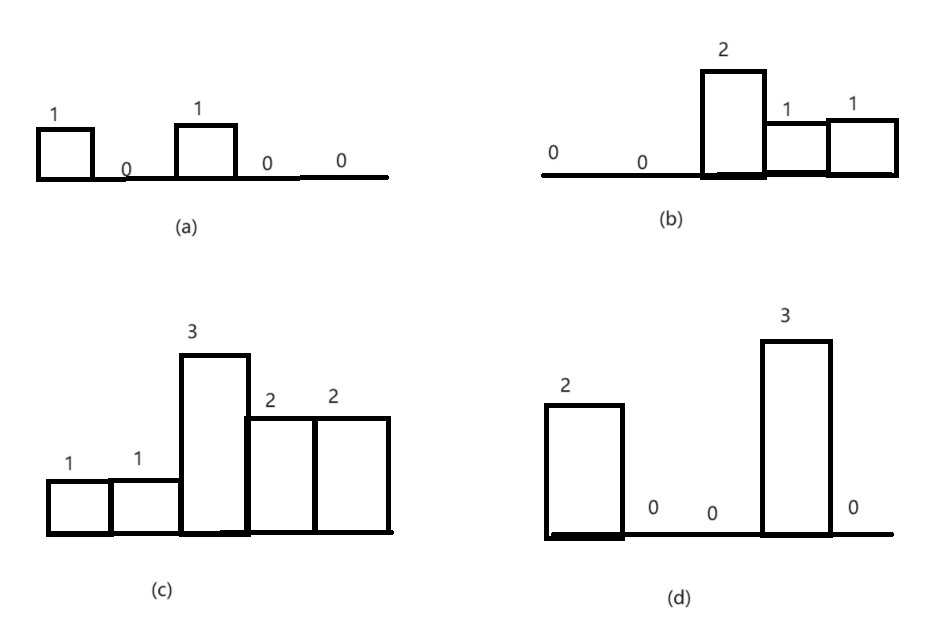
说明:(a)以矩阵第一行为基线的直方图;(b)以矩阵第二行为基线的直方图;(c)以矩阵第三行为基线的直方图;(d)以矩阵第四行为基线的资方图。
暴力解法(可取)
class Solution {
public:int maximalRectangle(vector<string>& matrix) {if(matrix.size()==0 || matrix[0].size()==0) return 0;int m=matrix[0].size();vector<int> v(m);int mxarea=0;for(string s:matrix){for(int i=0;i<m;i++){if(s[i]=='0') v[i]=0;else v[i]++;}mxarea=max(mxarea,maxarea(v));}return mxarea;}int maxarea(vector<int>& heights) {int n=heights.size();int maxarea=0;for(int i=0;i<n;i++){int minheight=heights[i];for(int j=i;j<n;j++){minheight=min(minheight,heights[j]);int area=minheight*(j-i+1);maxarea=max(maxarea,area);}}return maxarea;}
};分治法(可取)
class Solution {
public:int maximalRectangle(vector<string>& matrix) {if(matrix.size()==0 || matrix[0].size()==0) return 0;int m=matrix[0].size();vector<int> v(m);int mxarea=0;for(string s:matrix){for(int i=0;i<m;i++){if(s[i]=='0') v[i]=0;else v[i]++;}mxarea=max(mxarea,maxarea(v));}return mxarea;}int maxarea(vector<int>& heights) {return helper(heights,0,heights.size()-1);}int helper(vector<int>& heights,int start,int end){if(start>end) return 0;else if(start==end) return heights[start];else{int minindex=start;for(int i=start+1;i<=end;i++){if(heights[i]<heights[minindex])minindex=i;}int area=(end-start+1)*heights[minindex];int left=helper(heights,start,minindex-1);int right=helper(heights,minindex+1,end);return max(area,max(left,right));}}
};单调栈法(可取)
class Solution {
public:int maximalRectangle(vector<string>& matrix) {if(matrix.size()==0 || matrix[0].size()==0) return 0;int m=matrix[0].size();vector<int> v(m);int mxarea=0;for(string s:matrix){for(int i=0;i<m;i++){if(s[i]=='0') v[i]=0;else v[i]++;}mxarea=max(mxarea,maxarea(v));}return mxarea;}int maxarea(vector<int> v){stack<int> st;st.push(-1);int area=0;for(int i=0;i<v.size();i++){while(st.top()!=-1 && v[i]<=v[st.top()]){int height=v[st.top()];st.pop();int width=i-st.top()-1;area=max(area,height*width);}st.push(i);}while(st.top()!=-1){int height=v[st.top()];st.pop();int width=v.size()-st.top()-1;area=max(area,height*width);}return area;}
};相关文章:

最大矩形问题
柱状图中最大的矩形 题目 分析 矩形的面积等于宽乘以高,因此只要能确定每个矩形的宽和高,就能计算它的面积。如果直方图中一个矩形从下标为 i 的柱子开始,到下标为 j 的柱子结束,那么这两根柱子之间的矩形(含两端的柱…...

LeetCode62不同路径
题目描述 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。问总共有多少条不同的路径? …...
GNU Radio实现OFDM Radar
文章目录 前言一、GNU Radio Radar Toolbox编译及安装二、ofdm radar 原理讲解三、GNU Radio 实现 OFDM Radar1、官方提供的 grc①、grc 图②、运行结果 2、修改后的便于后续可实现探测和通信的 grc①、grc 图②、运行结果 四、资源自取 前言 本文使用 GNU Radio 搭建 OFDM Ra…...

东方博宜1760 - 整理抽屉
题目描述 期末考试即将来临,小T由于同时肩负了学习、竞赛、班团活动等多方面的任务,一直没有时间好好整理他的课桌抽屉,为了更好地复习,小T首先要把课桌抽屉里的书分类整理好。 小T的抽屉里堆着 N 本书,每本书的封面上…...
react快速开始(四)-之Vite 还是 (Create React App) CRA? 用Vite创建项目
文章目录 react快速开始(四)-之Vite 还是 (Create React App) CRA? 用Vite创建项目背景Vite 和 (Create React App) CRAVite?Vite 是否支持 TypeScript? 用Vite创建react项目参考 react快速开始(四)-之Vite 还是 (Create React App) CRA? 用Vite创建项…...
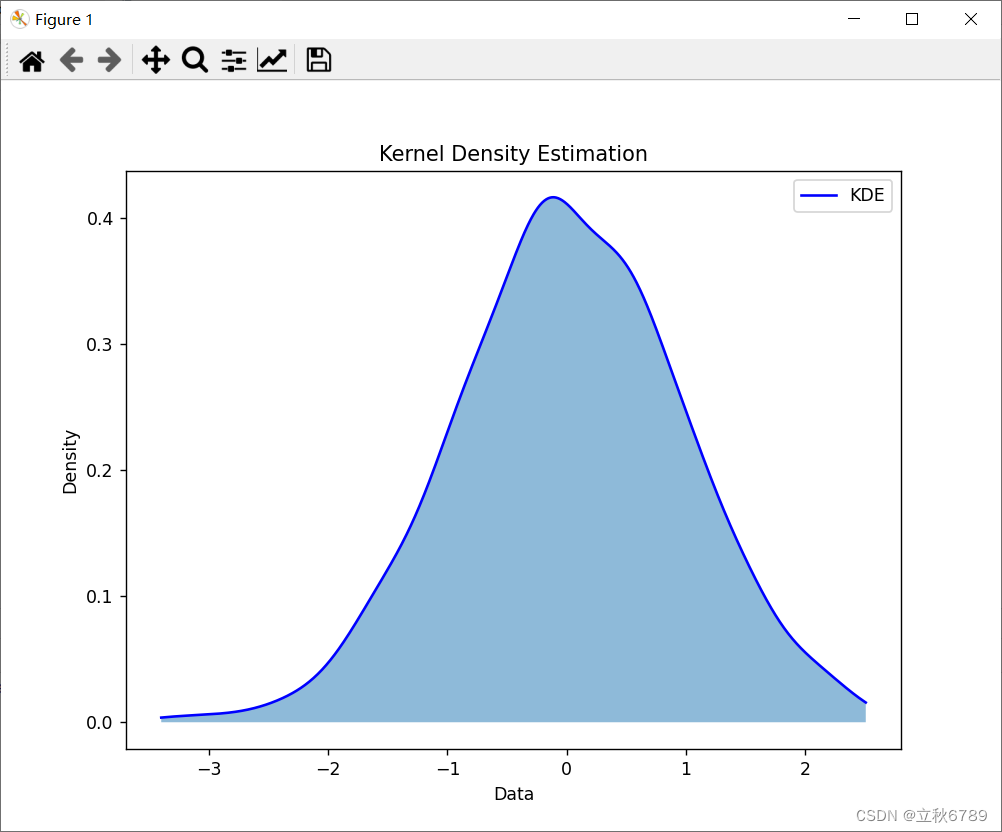
使用python绘制核密度估计图
使用python绘制核密度估计图 核密度估计图介绍效果代码 核密度估计图介绍 核密度估计(Kernel Density Estimation,KDE)是一种用于估计数据概率密度函数的非参数方法。与直方图不同,KDE 可以生成平滑的密度曲线,更好地…...
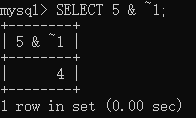
5. MySQL 运算符和函数
文章目录 【 1. 算术运算符 】【 2. 逻辑运算符 】2.1 逻辑非 (NOT 或者 !)2.2 逻辑与运算符 (AND 或者 &&)2.3 逻辑或 (OR 或者 ||)2.4 异或运算 (XOR) 【 3. 比较运算符 】3.1 等于 3.2 安全等于运算符 <>3.3 不等于运算符 (<> 或者 !)3.4 小于等于运算符…...

Linux学习之vi文本编辑器的使用
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

【数据结构】链表与顺序表的比较
不同点: 顺序表和链表是两种常见的数据结构,他们的不同点在于存储方式和插入、删除操作、随机访问、cpu缓存利用率等方面。 一、存储方式不同: 顺序表: 顺序表的存储方式是顺序存储,在内存中申请一块连续的空间,通…...

dart 基本语法
//入口方法 main() 或 void main() //数据类型 原生数据类型 String int double bool null 注意:String 包函 ‘’ “” ‘’’ ‘’’ 三种形式复杂数据类型 list Set Map自定义数据类型 class inheritance动态数据类型 var 注:dart 是静态类型语言&a…...
)
【经验分享】嵌入式入坑经历(选段)
文章目录 你现在的工作中所用到的专业知识有哪些呢?为什么想转行了?后来为什么从事了嵌入式行业呢?你对嵌入式的兴趣是何时培养起来的?你是怎么平衡兴趣爱好和工作的关系的?平时做的事情对你现在的工作有哪些帮助?对于有志学习嵌入式开发的在校大学生…...

Docker面试整理-Docker与虚拟机的区别是什么?
Docker 容器和传统的虚拟机(VM)都是提供隔离的运行环境以部署和运行应用程序的技术,但它们在架构和性能上存在显著的不同。了解这些差异可以帮助你选择最适合特定需求的解决方案: 基础架构:虚拟机:每个虚拟机都包括完整的操作系统、应用程序、必需的库和二进制文件,运行在…...

Java:JDK8 GC中ParNew和CMS的问题说明
JDK8中常用如下的垃圾收集器,它们分别运用在年轻代和老年代: ParNew : 年轻代垃圾收集器,多线程,采用标记—复制算法。 CMS:老年代的收集器,全称(Concurrent Mark and Sweep)&#…...
学单片机前先学什么?
先学c语言和数字电路 这里默认你说的单片机是51单片机,通过你的问题,我猜你的单片机应该还没有入门,如果是入门的话,一般都是从51单片机开始的。刚好我有一些资料,是我根据网友给的问题精心整理了一份「单片机的资料从…...

数据可视化:Matplotlib 与 Seaborn
数据可视化是数据分析中至关重要的一部分,它能帮助我们直观地理解数据的分布、趋势和关系。Python 中,Matplotlib 和 Seaborn 是两个最常用的可视化库。本文将详细介绍如何使用 Matplotlib 和 Seaborn 进行数据可视化,包括基本图形、图形定制…...

【linux】自定义快捷命令/脚本
linux自定义快捷命令 场景自定义命令自定义脚本 场景 深度学习经常要切换到自己环境,conda activate mmagic,但是又不想每次重复打这么多字,想使用快捷命令直接切换。 自定义命令 使用别名(alias)或自定义脚本来创建…...

使用onnxruntime加载YOLOv8生成的onnx文件进行目标检测
在网上下载了60多幅包含西瓜和冬瓜的图像组成melon数据集,使用 LabelMe 工具进行标注,然后使用 labelme2yolov8 脚本将json文件转换成YOLOv8支持的.txt文件,并自动生成YOLOv8支持的目录结构,包括melon.yaml文件,其内容…...
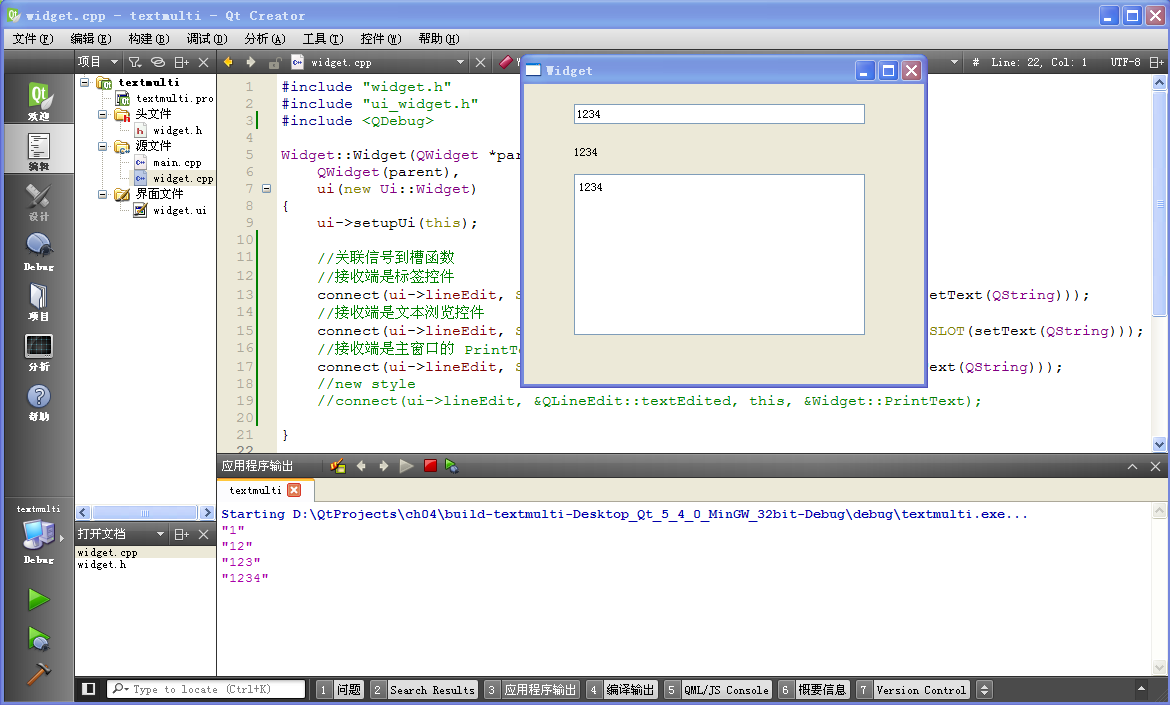
QT 信号和槽 一对多关联示例,一个信号,多个槽函数响应,一个信号源如何绑定多个槽函数
在窗体里放置一个单行文本编辑控件(QLineEdit)、一个标签控件(QLabel)和一个文本浏览控件(QTextBrowser),在单行文 本编辑控件里的文本被编辑时,标签控件和文本浏览控件都会同步显示…...

C++ AVL树 详细讲解
目录 一、AVL树的概念 二、AVL树的实现 1.AVL树节点的定义 2.AVL树的插入 3.AVL树的旋转 4.AVL树的验证 三、AVL树的性能 四、完结撒❀ 一、AVL树的概念 二叉搜索树虽可以缩短查找的效率,但 如果数据有序或接近有序二叉搜索树将退化为单支树,查 …...

Faster R-CNN:端到端的目标检测网络
本文回顾了由微软研究人员开发的 Faster R-CNN 模型。Faster R-CNN 是一种用于物体检测的深度卷积网络,在用户看来,它是一个单一的、端到端的统一网络。该网络可以准确快速地预测不同物体的位置。为了真正理解 Faster R-CNN,我们还必须快速概…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
