排序算法案例
排序算法概述
- 排序算法是计算机科学中的一个重要主题,用于将一组数据按特定顺序排列。排序算法有很多种,每种算法在不同情况下有不同的性能表现。
- 不同的排序算法适用于不同的场景和数据特征。在选择排序算法时,需要考虑数据规模、数据分布以及性能要求。了解各种排序算法的原理和实现方法有助于在实际应用中选择最合适的排序方法。
以下是一些常见的排序算法:
1.冒泡排序(Bubble Sort)
原理:反复遍历要排序的列表,每次比较相邻的两个元素,如果顺序错误就交换,直到没有需要交换的元素为止。
时间复杂度:最坏和平均情况下都是 𝑂(𝑛2)
空间复杂度:O(1)
def bubble_sort(arr):n = len(arr)for i in range(n):for j in range(0, n-i-1):if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]return arr2.选择排序(Selection Sort)
原理:每次从未排序部分选择最小的元素,放到已排序部分的末尾。
时间复杂度:最坏和平均情况下都是 𝑂(𝑛2)
空间复杂度:𝑂(1)
def selection_sort(arr):n = len(arr)for i in range(n):min_idx = ifor j in range(i+1, n):if arr[j] < arr[min_idx]:min_idx = jarr[i], arr[min_idx] = arr[min_idx], arr[i]return arr
3.插入排序(Insertion Sort)
原理:构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
时间复杂度:最坏和平均情况下都是
𝑂(𝑛2),最佳情况(已排序)是 𝑂(𝑛)
空间复杂度:𝑂(1)
def insertion_sort(arr):for i in range(1, len(arr)):key = arr[i]j = i-1while j >= 0 and key < arr[j]:arr[j + 1] = arr[j]j -= 1arr[j + 1] = keyreturn arr
4.归并排序(Merge Sort)
原理:采用分治法,将数组分成两个子数组,分别排序后合并。
时间复杂度:最坏和平均情况下都是 𝑂(𝑛log𝑛)
空间复杂度:O(n)
def merge_sort(arr):if len(arr) > 1:mid = len(arr) // 2L = arr[:mid]R = arr[mid:]merge_sort(L)merge_sort(R)i = j = k = 0while i < len(L) and j < len(R):if L[i] < R[j]:arr[k] = L[i]i += 1else:arr[k] = R[j]j += 1k += 1while i < len(L):arr[k] = L[i]i += 1k += 1while j < len(R):arr[k] = R[j]j += 1k += 1return arr
5.快速排序(Quick Sort)
原理:采用分治法,选择一个基准元素,将数组分成两部分,一部分比基准小,一部分比基准大,然后递归排序两部分。
时间复杂度:最坏情况下是 O(n2),平均情况下是 O(nlogn)。
空间复杂度:O(logn)(递归调用栈)
def partition(arr, low, high):pivot = arr[high]i = low - 1for j in range(low, high):if arr[j] <= pivot:i = i + 1arr[i], arr[j] = arr[j], arr[i]arr[i + 1], arr[high] = arr[high], arr[i + 1]return i + 1def quick_sort(arr, low, high):if low < high:pi = partition(arr, low, high)quick_sort(arr, low, pi - 1)quick_sort(arr, pi + 1, high)return arr6. 希尔排序(Shell Sort)
原理:改进版的插入排序,通过将数据按一定间隔分组,对每组进行插入排序,然后逐渐减少间隔进行多次排序。
时间复杂度:最坏情况下是 O(n2),但通常比插入排序快得多。
空间复杂度:O(1)
def shell_sort(arr):n = len(arr)gap = n // 2while gap > 0:for i in range(gap, n):temp = arr[i]j = iwhile j >= gap and arr[j - gap] > temp:arr[j] = arr[j - gap]j -= gaparr[j] = tempgap //= 2return arr
7. 堆排序(Heap Sort)
原理:利用堆这种数据结构来排序,首先将数组构建成最大堆,然后将堆顶元素(最大值)与末尾元素交换,再对剩余元素进行堆调整,重复此过程。
时间复杂度:最坏和平均情况下都是O(nlogn)
空间复杂度:O(1)
def heapify(arr, n, i):largest = il = 2 * i + 1r = 2 * i + 2if l < n and arr[i] < arr[l]:largest = lif r < n and arr[largest] < arr[r]:largest = rif largest != i:arr[i], arr[largest] = arr[largest], arr[i]heapify(arr, n, largest)def heap_sort(arr):n = len(arr)for i in range(n // 2 - 1, -1, -1):heapify(arr, n, i)for i in range(n - 1, 0, -1):arr[i], arr[0] = arr[0], arr[i]heapify(arr, i, 0)return arr8. 计数排序(Counting Sort)
原理:适用于整数排序,通过计数数组记录每个整数的出现次数,然后按照顺序输出。
时间复杂度:O(n+k),其中 𝑘是数列中的最大值
空间复杂度:O(k)
def counting_sort(arr):max_val = max(arr)m = max_val + 1count = [0] * m for a in arr:count[a] += 1 i = 0for a in range(m): for c in range(count[a]): arr[i] = ai += 1return arr9. 桶排序(Bucket Sort)
原理:将数组分成若干个桶,每个桶内的元素分别进行排序,然后合并所有桶内的元素得到有序序列。
时间复杂度:最坏情况下是
O(n2),但通常情况下是 O(n+k)
空间复杂度:O(n+k)
def bucket_sort(arr):bucket = []slot_num = 10 for i in range(slot_num):bucket.append([])for j in arr:index_b = int(slot_num * j)bucket[index_b].append(j)for i in range(slot_num):bucket[i] = insertion_sort(bucket[i])k = 0for i in range(slot_num):for j in range(len(bucket[i])):arr[k] = bucket[i][j]k += 1return arr10. 基数排序(Radix Sort)
原理:按照个位、十位、百位等进行多次排序,每次排序使用稳定的排序算法(如计数排序)。
时间复杂度:
O(nk),其中k 是数的位数。
空间复杂度:O(n+k)
def counting_sort_for_radix(arr, exp1):n = len(arr)output = [0] * n count = [0] * 10for i in range(0, n):index = arr[i] // exp1count[index % 10] += 1for i in range(1, 10):count[i] += count[i - 1]i = n - 1while i >= 0:index = arr[i] // exp1output[count[index % 10] - 1] = arr[i]count[index % 10] -= 1i -= 1for i in range(0, len(arr)):arr[i] = output[i]def radix_sort(arr):max1 = max(arr)exp = 1while max1 / exp > 1:counting_sort_for_radix(arr, exp)exp *= 10return arr
- 调用测试
arr = [1,4,3,0,2]
print(f'冒泡排序:{bubble_sort(arr)}')
print(f'选择排序:{selection_sort(arr)}')
print(f'插入排序:{insertion_sort(arr)}')
print(f'归并排序:{merge_sort(arr)}')
print(f'快速排序:{quick_sort(arr,0,4)}')
print(f'希尔排序:{shell_sort(arr)}')
print(f'堆排序: {heap_sort(arr)}')
print(f'计数排序:{counting_sort(arr)}')
print(f'桶排序:{bucket_sort([num/10 for num in arr])}')
print(f'基数排序:{radix_sort(arr)}')
冒泡排序:[0, 1, 2, 3, 4]
选择排序:[0, 1, 2, 3, 4]
插入排序:[0, 1, 2, 3, 4]
归并排序:[0, 1, 2, 3, 4]
快速排序:[0, 1, 2, 3, 4]
希尔排序:[0, 1, 2, 3, 4]
堆排序: [0, 1, 2, 3, 4]
计数排序:[0, 1, 2, 3, 4]
桶排序:[0.0, 0.1, 0.2, 0.3, 0.4]
基数排序:[0, 1, 2, 3, 4]
相关文章:

排序算法案例
排序算法概述 排序算法是计算机科学中的一个重要主题,用于将一组数据按特定顺序排列。排序算法有很多种,每种算法在不同情况下有不同的性能表现。不同的排序算法适用于不同的场景和数据特征。在选择排序算法时,需要考虑数据规模、数据分布以…...

时间序列评价指标
评价指标 均方误差( M S E MSE MSE) 定义:预测值与实际值之间差异的平方和的平均值。公式: ( M S E 1 n ∑ i 1 n ( y i − y ^ i ) 2 ) (MSE \frac{1}{n}\sum_{i1}^{n}(y_i - \hat{y}_i)^2) (MSEn1∑i1n(yi−y^i)…...
Docker:安装 Orion-Visor 服务器运维的技术指南
请关注微信公众号:拾荒的小海螺 博客地址:http://lsk-ww.cn/ 1、简述 Orion-Visor 是一种用于管理和监控容器的工具。它提供了一个直观的界面,用于查看容器的状态、资源使用情况以及日志等信息。在这篇技术博客中,我们将介绍如何…...
HarmonyOS Next 系列之底部标签栏TabBar实现(三)
系列文章目录 HarmonyOS Next 系列之省市区弹窗选择器实现(一) HarmonyOS Next 系列之验证码输入组件实现(二) HarmonyOS Next 系列之底部标签栏TabBar实现(三) 文章目录 系列文章目录前言一、实现原理二、…...
mac怎么录制屏幕?这2个方法你值得拥有
在数字化时代,屏幕录制已经成为一种常见且重要的工具,无论是教学演示、游戏直播还是会议记录,屏幕录制都发挥着不可或缺的作用。对于Mac用户而言,如何高效、便捷地进行屏幕录制,是一个值得探讨的话题,可是很…...

爱德华三坐标软件ACdmis.AC-dmis密码注册机
爱德华三坐标软件 AC-DMIS 是一款功能强大的三坐标测量软件,具有以下特点: • 支持多种测量模式:包括接触式测量、非接触式测量、复合式测量等,可以满足不同类型工件的测量需求。 • 高精度测量:采用先进的测量算法和…...

计算机网络 期末复习(谢希仁版本)第3章
对于点对点的链路,目前使用得最广泛的数据链路层协议是点对点协议 PPP (Point-to-Point Protocol)。局域网的传输媒体,包括有线传输媒体和无线传输媒体两个大类,那么有线传输媒体有同轴电缆、双绞线和光纤;无线传输媒体有微波、红…...

代码随想录——数组
给定一个n个元素有序(升序)的整型数组nums和一个目标值target,写一个函数搜索nums中的target,如果目标值存在返回下标,否则返回-1. //这个题说实话从逻辑上来看实在是太简单了,但是为什么每一次我写起来都感…...
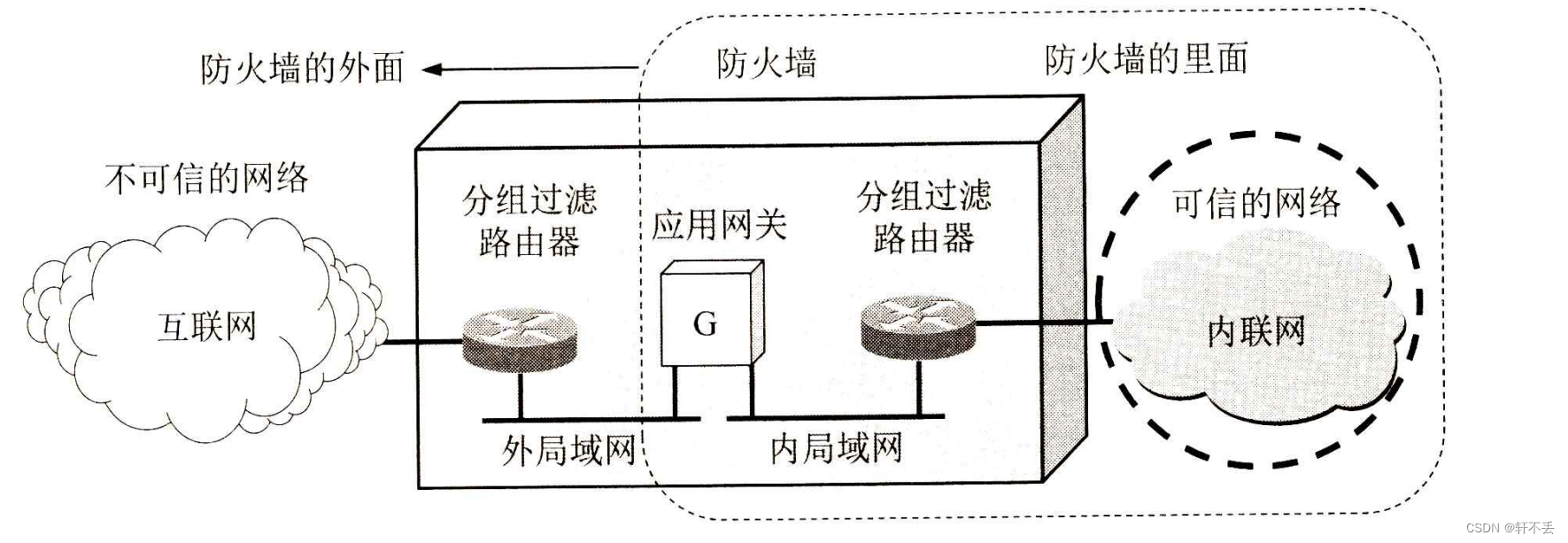
计算机网络7——网络安全4 防火墙和入侵检测
文章目录 一、系统安全:防火墙与入侵检测1、防火墙1)分组过滤路由器2)应用网关也称为代理服务器(proxy server), 二、一些未来的发展方向 一、系统安全:防火墙与入侵检测 恶意用户或软件通过网络对计算机系统的入侵或攻击已成为当今计算机安…...

html+CSS+js部分基础运用20
根据下方页面效果如图1所示,编写程序,代码放入图片下方表格内 图1.效果图 <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta http-equiv"X-UA-Compatible" conte…...

ISO 19115-2:2019 附录C XML 模式实现
C.1 XML 模式 本文件中定义的 UML 模型的 XML 模式在 ISO/TS 19115-3 中定义的适当 XML 命名空间中提供。新增内容包括: 命名空间前缀模式文件名Metadata for ACquisition (mac)acquisitionInformationImagery.xsdMetadata for Resource Content (mrc)contentInfo…...
)
DevOps的原理及应用详解(一)
本系列文章简介: 在当今快速变化的商业环境中,企业对于软件交付的速度、质量和安全性要求日益提高。传统的软件开发和运维模式已经难以满足这些需求,因此,DevOps(Development和Operations的组合)应运而生&a…...
)
【冲刺秋招,许愿offer】第 三 天(水一天)
【冲刺秋招,许愿offer】第 二 天(水一天) 知识点牛客emo 知识点 今天端午,上午去摘杏下午理发,一天没咋看电脑。晚上刷刷LeetCode看看八股。 牛客 spring事务失效的情况 捕获到异常,自己手动处理 方法修…...
使用 C# 学习面向对象编程:第 6 部分
继承 亲爱的读者,继承意味着从源头继承一些东西。例如,儿子可以继承父亲的习惯。同样的概念也用于面向对象编程;它是 OOP 的第二大支柱。 继承允许创建一个新类,该新类继承另一个类或基类的属性,继承这些成员的类称为…...
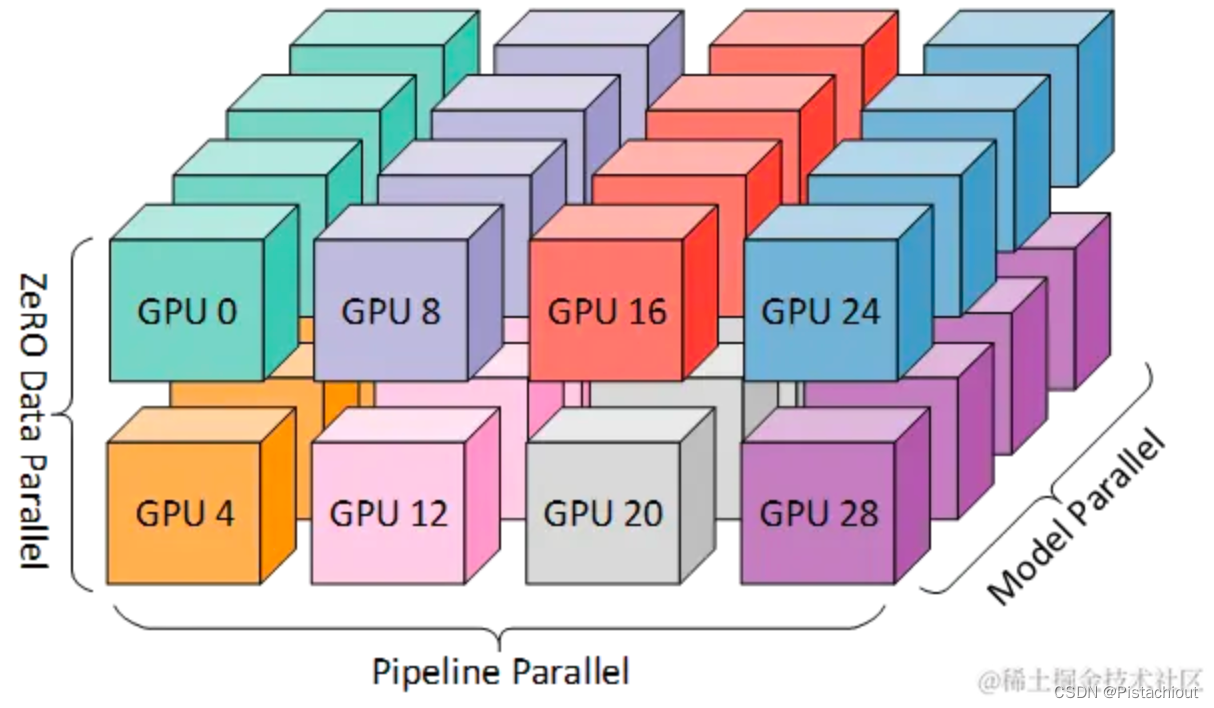
分布式训练基础入门
1.单节点训练 单节点训练也会转换为等价的并行训练,如在GPU内同一wrap内的32个Thread执行同一指令,但处理不同的数据。 训练程序往往实现了一个多层神经网络的执行过程。该神经网络的执行由一个计算图(Computational Graph)表示。…...
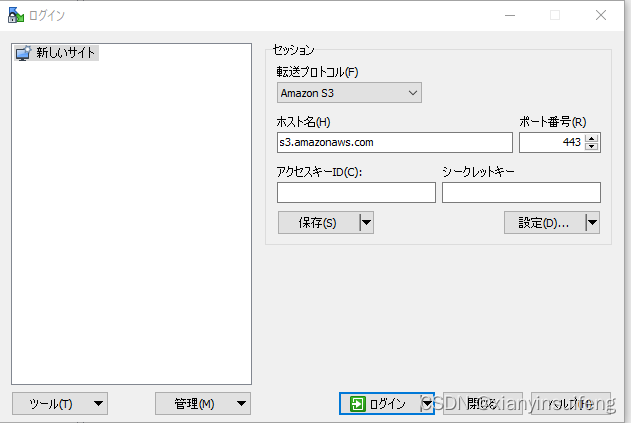
AWS S3存储桶中如何下载文件
AWS S3存储桶中如何下载文件 1.单个下载 AWS S3 控制台提供了下载单个文件的功能,但是不支持直接在控制台中进行批量下载文件。您可以通过以下步骤在 AWS S3 控制台上下载单个文件: 1.1登录 AWS 管理控制台。 1.2转到 S3 服务页面。 1.3单击…...
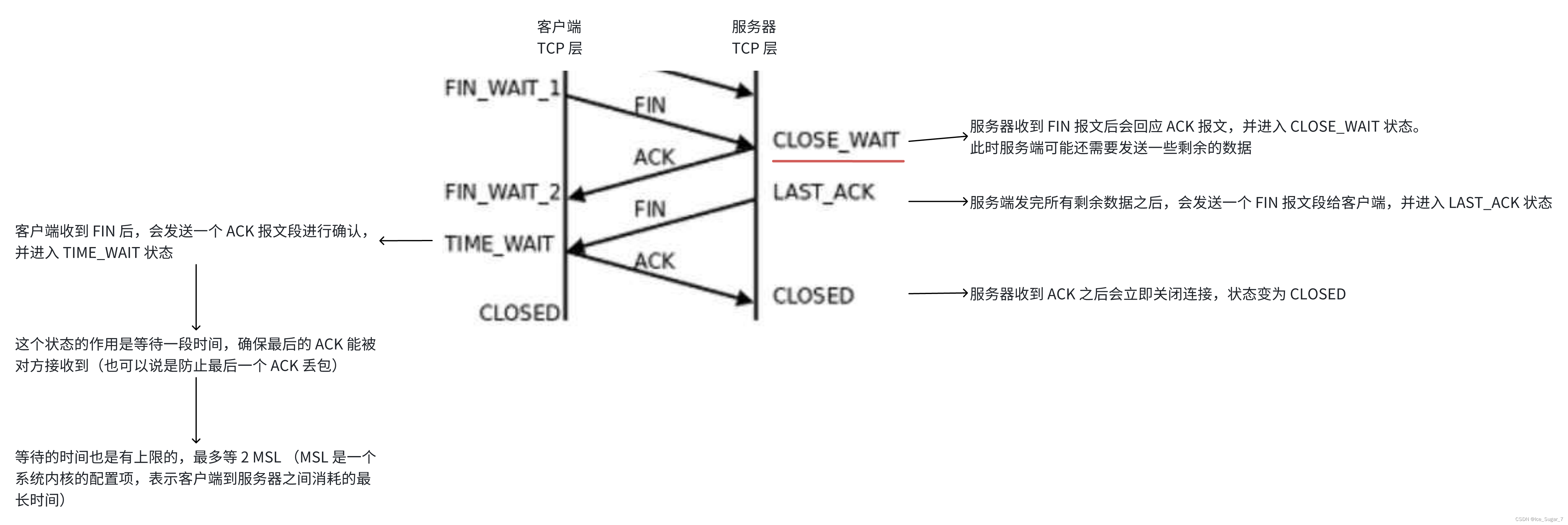
「网络原理」三次握手四次挥手
🎇个人主页:Ice_Sugar_7 🎇所属专栏:计网 🎇欢迎点赞收藏加关注哦! 三次握手&四次挥手 🍉连接管理🍌三次握手🍌意义🍌四次挥手🍌TCP 状态转换…...

第二十四章 SOAP 错误处理 - 发生故障时添加 WS-Addressing 标头元素
文章目录 第二十四章 SOAP 错误处理 - 发生故障时添加 WS-Addressing 标头元素%SOAP.Fault12.Code 属性SubcodeValue %SOAP.Fault12.Text 属性Textlang 发生故障时添加 WS-Addressing 标头元素 第二十四章 SOAP 错误处理 - 发生故障时添加 WS-Addressing 标头元素 %SOAP.Fault…...

CSS真题合集(一)
CSS真题合集(一) 1. 盒子模型1.1 盒子模型的基本组成1.2 盒子模型的实际大小1.3 盒子模型的两种类型1.4 设置盒子模型1.5 弹性盒子模型 2. BFC2.1 主要用途2.2 触发BFC的方法2.2 解决外边距的塌陷问题(垂直塌陷) 3. 响应式布局3.1…...
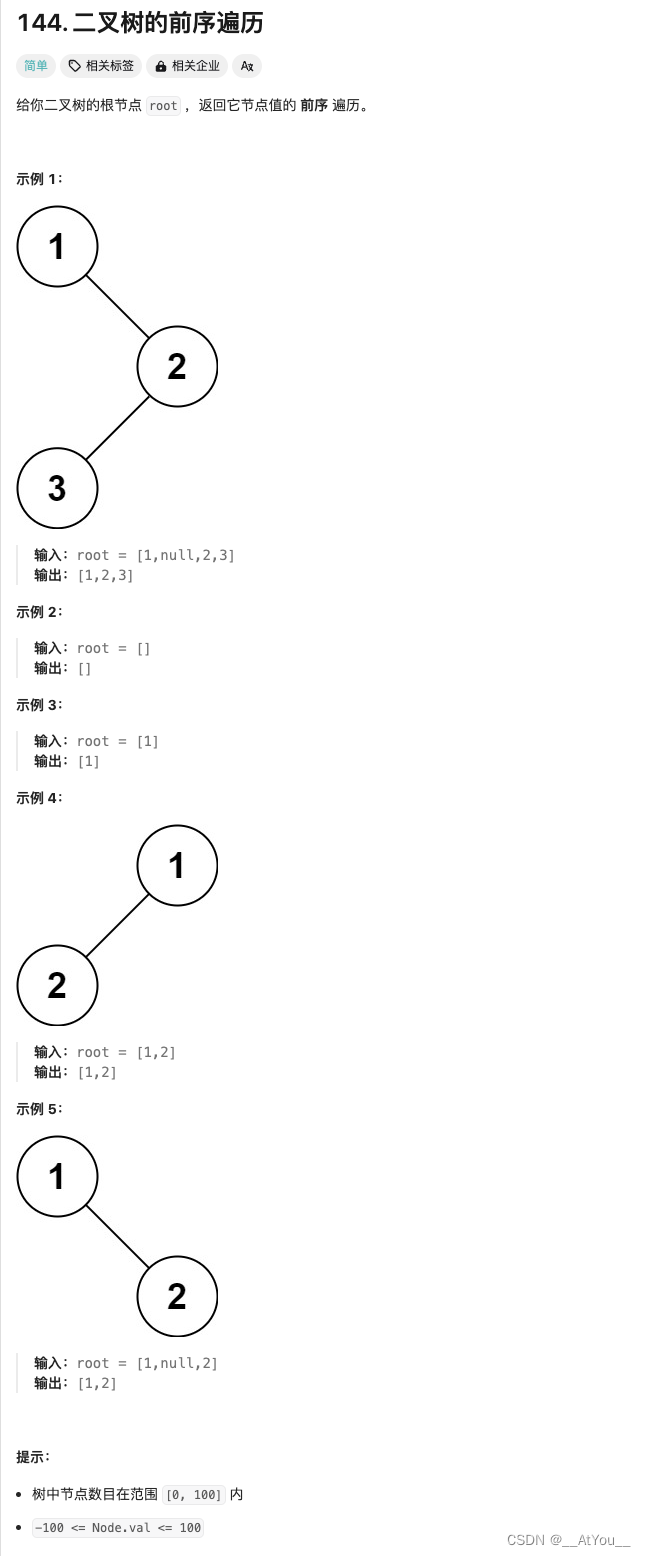
Golang | Leetcode Golang题解之第144题二叉树的前序遍历
题目: 题解: func preorderTraversal(root *TreeNode) (vals []int) {var p1, p2 *TreeNode root, nilfor p1 ! nil {p2 p1.Leftif p2 ! nil {for p2.Right ! nil && p2.Right ! p1 {p2 p2.Right}if p2.Right nil {vals append(vals, p1.V…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...
